基于贝叶斯网络的复杂产品设计过程知识挖掘方法

王明微 ，韩绍欢，刘晓晨，李曙光

WANG Ming-wei1 , HAN Shao-huan2 , LIU Xiao-chen3, LI Shu-guang1

（1.西北工业大学 现代设计与集成制造技术教育部重点实验室，西安 710072；2.中国空间技术研究院，北京 100094；3.航天人才开发交流中心，北京 100830）

0 引言

目前，在我国以卫星、飞机为代表的飞行器总体设计中对功能分析、技术要求分配等设计活动，仍然主要依赖于个人经验进行主观判断与协调；严格的评审程序只能保证最终设计结果的正确性，而忽略了设计整体实现过程，难以追溯问题产生根源。因此，获取复杂产品设计过程中设计元素之间的因果知识，将产品开发过程从依赖个人经验转变为严谨、有规律可循的科学实践，对于提高产品设计效率和质量具有重要意义和作用。

贝叶斯网络（Bayesian networks）[1,2]作为数据挖掘技术中的最重要理论工具之一，能够以条件概率方式确定变量之间的因果依赖关系，直观和全面地综合分析影响决策的所有因素。目前，国内外学者在不同领域对基于贝叶斯网络的因果知识表达、获取和推理展开了大量的研究。例如文献[3]尝试利用因果图构建贝叶斯网络，并比较二者异同；文献[4]给出常见的贝叶斯网络学习因果关系知识模型的假设条件；文献[5]通过贝叶斯网建立了设备故障原因与故障模型的因果关系；文献[6]针对海岸安全评估问题建立了一个贝叶斯网络模型用于表述问题中的因果关系，并提出了一个五层结构框架用于预测潜在风险。

由于复杂产品设计过程是一个涉及多约束、多问题域复杂问题，在因果传播机理、内部关联关系及决策过程等方面都有其自身特点，很难直接利用贝叶斯网络模型描述复杂开发开发过程，影响了因果知识提取的效果，迫切需要解决以下关键问题：

1）随着开发活动的深入，设计元素间的耦合程度急剧上升，单纯依靠设计人员认知能力无法准确分析出各种设计状态和设计结果之间的内涵和关联。如何将贝叶斯网络的基本要素（节点、有向边、概率分布、状态、事件等）与复杂的产品开发过程关联起来，能够准确且简洁地描述设计元素间不确定的因果关系，是需要解决的基本问题。

2）虽然一些显性映射规则能够直接建立设计元素之间的因果联系，但是总体来说设计元素之间的因果映射需要设计人员根据设计原理和自身经验才能建立。这种经验规则蕴含在设计实例中，具有模糊性和不确定性。如何将设计人员的经验信息与历史设计数据相融合，并充分利用产品开发特点（例如具有一定的层次性），是提高知识获取效果的关键。

因此，本文基于分层映射的产品开发过程思想[7,8]，提出基于贝叶斯网络的产品开发过程因果知识表达模型和知识获取方法，通过融合设计人员先验知识和已有产品设计数据，从定量和定性二个角度实现设计要素之间隐含因果关系的显性化。

1 基于贝叶斯网络的设计过程因果知识模型

1.1 因果知识模型PDCKM定义

分层映射模型是最常用的产品开发过程的形式化表达和规律性描述，它通过将产品开发过程进行层次划分，将复杂问题的求解分解为多个子问题域并进行层次化推理求解[8]。这意味着产品开发过程因果知识具有一定的层次性。同时，从飞行器总体设计过程全局角度来看，不仅仅单纯关注于设计元素间的两两映射，总体设计过程所有设计元素的因果联系呈现出网状拓扑结构。因此，本文在贝叶斯网络的基础上进行功能扩展，提出一种面向复杂产品总体设计的产品开发过程因果知识模型PDCKM（Product Development Causal Knowledge Model），表达不同问题域各设计元素的因果影响、因果影响传递以及因果影响程度，通过前向节点对后向节点状态的递推作用来实现产品开发过程的模拟。

定义1[产品设计过程因果知识模型]（Product Development Causal Knowledge Model）采用有向图方式表达开发过程中各种设计要素以及其因果关系的一种知识模型，以三元组来表达，其中：X={X1,…,Xn}是图中所有节点对应的设计要素变量集合，表达了产品开发设计过程中各种设计要素及其可行状态取值；E={[eij],1≤i≤n,1≤j≤n,i≠j} 是图中连接各个变量节点有向边集合，表示各个变量节点之间的因果关系。eij表示一条由节点Xi到Xj的有向边，即设计元素Xi的状态变化会影响到设计元素Xj的状态。P={p(Xi|Pa(Xi)}是图中与各个节点有关的条件概率分布，从定量的角度描述了变量节点之间因果依赖关系的强度，Pa(Xi)为Xi的父节点集合。若Pa(Xi)为空，则表示该变量没有父变量，只需给出其先验概率分布。

1.2 节点变量类别

本文基于经典的功能-行为-结构层次模型[7]，将PDCKM中的节点变量X划分为3个无交集的集合：需求域变量子集R、功能域变量子集F、结构域变量子集S，即X=R∪F∪S。

1）需求域变量：需求域节点表达了用户对产品的设计要求，通过质量功能配置（QFD）等方法用一组可度量的参数来明确地描述产品应具有的基本需求特性。

2）功能域变量：功能域变量是为完成产品设计需求所必需具有的最小功能需求元素集合，表达了达到产品设计需求所必需的一系列行动。

3）结构域变量：结构域变量是满足功能域变量要求的产品物理结构元素的集，包括硬件类和软件类。结构域中的每一个元素至少应满足一项功能要求，或功能要求的一部分。当然一个结构元素也可满足多项功能要求。

1.3 有向边取向原则

PDCKM模型中的有向边集合E表示父节点Pa（Xi）对子节点具有直接因果影响，有向边的方向是进行决策推理的依据。为保证使PDCKM内含的条件独立性假设更为合适，本文基于分层映射模型思想，确定PDCKM中有向边取向规则如下：需求域变量只受其他需求变量的影响（即发生需求分解）；功能域变量可以受所有需求域变量以及其他功能域变量影响（即发生功能分解）；需求域变量和功能域变量将共同影响结构域变量。因此，确定PDCKM中有向边取向规则如下：

1.4 概率参数

PDCKM采用为节点变量计算以其父节点的状态取值为条件的概率分布，表示节点之间因果关系的连接强度，对于没有父节点的节点则需要给出其先验概率。如果有n个设计要素变量，并且当所有的设计要素变量均取二值时，需要2n-1个参数才能确定其联合概率分布，此计算量相当巨大。因此在PDCKM中可以充分利用变量间的条件独立关系，将联合分布分解成多个复杂度较低的条件概率分布，有如式(1)所示的联合概率计算公式，从而降低概率参数的表达复杂度，提高知识获取效率。

2 因果知识获取

基于数据的贝叶斯结构学习已经证明为NP-hard问题，本文采用最广泛应用的基于评分-搜索的结构学习算法。为在联合概率密度函数逼近程度和有向图模型复杂度之间取折衷，采用基于附加惩罚函数的最大互信息作为评分函数[9]，以改进的爬山算法获得最优的网络结构。

设：Bs是基于数据集D构建的一个贝叶斯网络结构，ri是变量Xi是的取值数，是父节点集Pa（Xi）的配置数目，则基于附加惩罚函数的最大互信息评分函数如式(2)所示：

其中，MI(Xi,Pa(Xi))为Xi和Pa(Xi)的条件互信息，如式(3)所示，文献[9]已证明使MI(Xi,Pa(Xi))最大的网络结构是对联合密度p(X1,…,Xn)的最佳逼近；dim(S)指拓扑结构Bs的复杂度，定义为拓扑结构Bs下有向图模型参数的最小数目

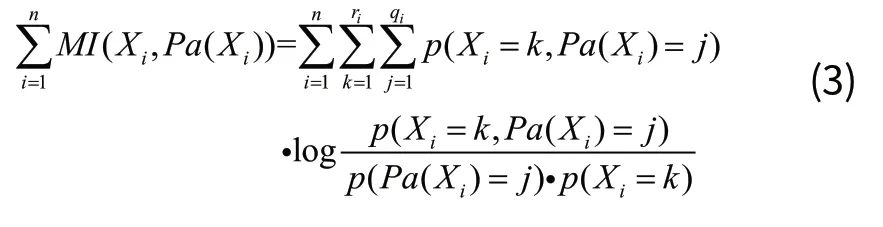
虽然完全基于专家经验建立PDCKM是不现实的，但是我们可以很容易利用专家已有经验知识，提高PDCKM获取的准确度和速度。这些先验知识主要包括：1）一个设计元素将受几个因素影响，即最大父节点数目，记为max(Pa(Xi)) ；2）部分设计要素变量间的偏序关系，从而判断节点之间的指向。所以本文除了采用爬山算法的加边算子、减边算子、换向算子，引入了修正算子，对候选PDCKM的拓扑结构进行修正。修正算子包括3个：1）消除环状回路算子：根据分层映射的产品开发过程思想，一般不考虑有回路的因果关系，如图1(a)所示；2）最大父节点算子：根据先验知识判断一个设计要素最大有多少个父节点，这样有利于减少搜索空间，如图1(b)所示；3）修正偏序关系算子：为了保证因果关系正确性，改正与先验知识不符的父子节点关系。

图1 PDCKM参数学习

对于PDCKM参数学习，当训练样本集完整时可以采用最大似然估计MLE进行参数估计，但是当样本数据不完整时，如当父结点样本数目为0时，MLE算法就会产生溢出问题，从而无法计算。在实际产品开发过程中，难免有些数据缺失。文献[10]证明了期望最大化算法EM从不完整的数据中进行参数学习比较有效，因此本文采用EM算法进行PDCKM参数学习。

在EM算法中第t次迭代过程中，第一步根据式(4)计算期望对数似然函数Q(θ|θt)，第二步是求得使Q(θ|θt)最大时候的θ。

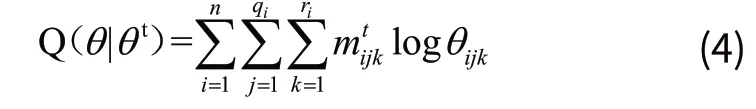
当θ取以下值时，Q(θ|θt)达到最大其中，其中是修补后数据中所有满足Xi=k和Pa(Xi)=j的样本的权重之和。

3 算例分析

本文以信标机系统为例，选取设计人员感兴趣的一组11个设计要素变量，通过收集国内外设计成功案例，提取出46个样本作为数据集。同时，根据领域专家经验确定部分先验知识，包括有向边的方向（如X1→X6）和最大父节点数目（如max(Pa(Xi)=5）。

采用基于最大互信息的启发式搜索算法得到PDCKM拓扑结构，如图2所示，可以看出天线（X7）只会载噪比（X8）参数。

基于所获取的PDCKM拓扑结构，采用EM算法进行PDCKM参数学习，获得PDCKM参数分布P，部分参数如表2所示，定量化的描述节点之间的因果依赖程度。

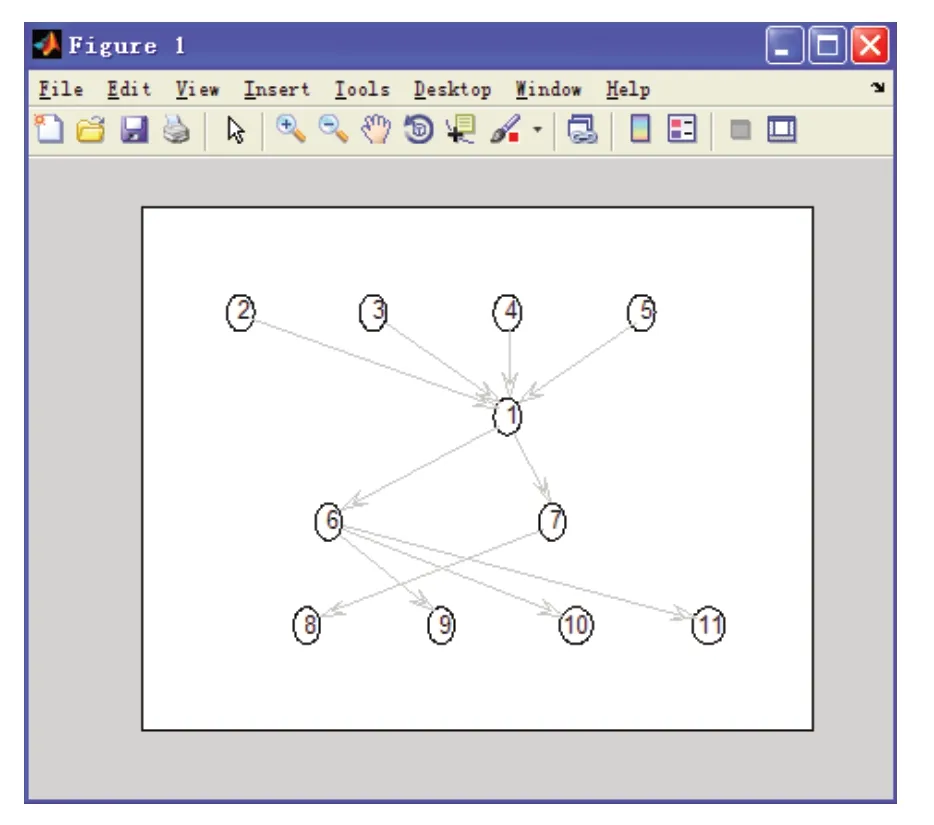
图2 PDCKM拓扑结构学习结果

通过实验结果，可以全面综合而直观的确定产品开发过程中各设计因素的因果关联关系，为进行正确决策奠定基础。同时，也可以提取概率较大的变量状态作为典型设计案例，为产品开发过程有规律可循的科学实践。

表2 PDCKM的部分参数

4 结束语

复杂产品开发过程各种设计元素因果关系具有模糊性和不确定性，本文提出了一种基于贝叶斯网络的产品开发过程过程知识提取方法。阐述了产品开发过程过程因果知识模型基本概念及模型组成部分，然后详细描述了模型结构学习和参数学习过程，从而能够依次提取概率较大的变量状态作为典型设计案例，为产品开发有规律可循的实现途径。

[1]Kim K Y,Kim Y S.Causal design knowledge:Alternative representation method for product development knowledge management[J].Computer-Aided Design,2011,43(9):1137-1153.

[2]慕春棣,戴剑彬,叶俊.用于数据挖掘的贝叶斯网络[J].软件学报,2000,11(5):660-666.

[3]Nadkarni S,Shenoy P P.A causal mapping approach to constructing Bayesian networks[J].Decision Support Systems,2004,38(2):259-281.

[4]Eckerman D.A tutorial on learning with Bayesian networks[M].Springer Berlin Heidelberg,2008.

[5]蔡志强,孙树栋,司书宾,王宁.基于贝叶斯网络的不确定环境装备故障推理模型[J].西北工业大学学报,2011,29(4):509-514.

[6]Ren J,Jenkinson I,Wang J,Xu D L,Yang J B.A methodology to model causal relationships on offshore safety assessment focusing on human and organizational factors.Journal of Safety Research,2008,39:87-100.

[7]Qian L,Gero J S.Function-Behavior-Structure path and their role in analogy-based design[J].AI EDAM,1996,10(4):289-312.

[8]王玉新,毛晓辉,李添益.功能-结构双向创新商空间模型关键技术研究[J].浙江大学学报(工学版),2010,44(8):1570-1578.

[9]李刚.知识发现的图模型方法[D].2000.

[10]M.Drudzzel.Qualitative Verbal Explanations Byaesian Belief Networks.In Artificial Intelligence and Simulation of Behaviour Quarterly[J].Special Issue on Bayesian Belief Networks.1996.94:43-54.