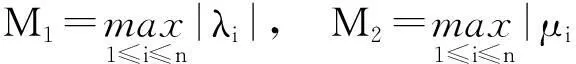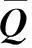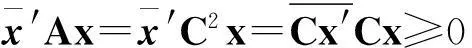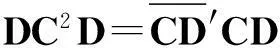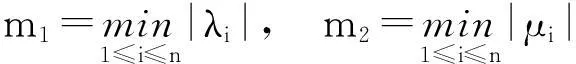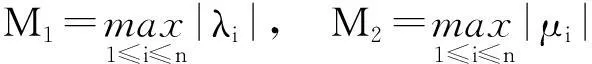华罗庚不等式在Hermite矩阵乘积的特征值估计中的应用

钟文体

(华南师范大学数学科学学院，广州510631)

华罗庚不等式在Hermite矩阵乘积的特征值估计中的应用

钟文体

(华南师范大学数学科学学院，广州510631)

[摘要]基于华罗庚在研究多复变函数时发现的一个行列式不等式给出Hermite矩阵乘积的特征值的估计.

[关键词]Hermite矩阵； 矩阵乘积； 特征值； 估计

1引言

设A是复数域上的n×n矩阵，这里用′表示A的共轭转置，det(A)表示A的行列式.

2主要结果

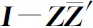
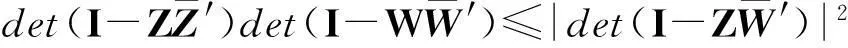
当且仅当Z=W时，等号成立.

引理2设A是复数域上的n阶方阵，λ1,λ2,…,λn是A的全部特征根(重根按重数计)，令f(x)是复数域上的次数大于1的多项式，则f(A)的全部特征根为f(λ1),f(λ2),…,f(λn).

引理3设A是复数域上的n阶可逆方阵，其全部特征值为λ1,λ2,…,λn(重根按重数计)，则A-1的全部特征值为,,…,.

这里略去引理2和引理3的证明，因为读者能在众多的参考文献中找到其证明.

由这几个引理，我们可以得到本文的第一个主要结果.

定理1设A和B是n阶可逆Hermite矩阵，设A的所有特征值为λ1,λ2,…,λn，B所有特征值为μ1,μ2,…,μn，记

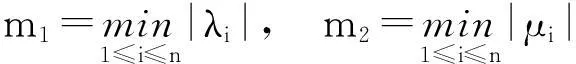
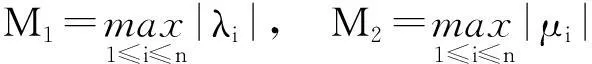
则对AB任一特征值v，都有|v|∈[m1m2,M1M2].

证分两步来证明这个定理.

(i) 设a是复数，且满足|a|>M1M2，则存在复数s,t使得a=st且|s|>M1，|t|>M2.由引理2,Hermite矩阵

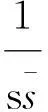
的所有特征值为

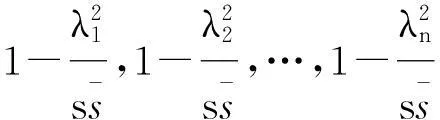
Hermite矩阵A的所有特征值λ1,λ2,…,λn都为实数，由假定，有

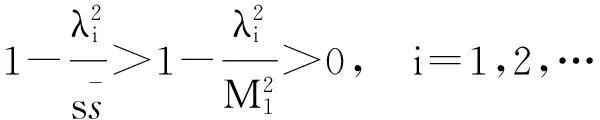
于是，矩阵

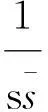
是正定Hermite矩阵.同理，矩阵

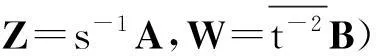
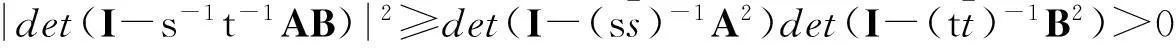
于是

|det(aI-AB)|2=|det(stI-AB)|2=s2nt2n|det(I-s-1t-1AB)|2≠0,

从而，矩阵aI-AB可逆，a不是AB的特征值.

(ii) 考虑矩阵A-1B-1.设a∈且满足0<|a|

于是，转化为(i)的情形，由(i)知|det(a-1I-A-1B-1)|2≠0，则

|det(AB-aI)|2=a2n|det(A)|2|det(a-1I-A-1B-1)|2|det(B)|2≠0,

从而矩阵AB-aI可逆，即aI-AB可逆，a不是AB的特征值.

综合(i)和(ii)可知，对AB的任一特征值v，有|v|∈[m1m2,M1M2].

从定理1的证明过程，可直接得到定理2.

定理2设A和B都是n阶Hermite矩阵，A或B不可逆.设A的所有特征值λ1,λ2,…,λn，B的所有特征值μ1,μ2,…,μn，记

则对AB的任一特征值v，都有|v|∈[0,M1M2].

在定理1和定理2中，AB的特征值v不一定是实数，有可能是虚数.但如果我们把条件加强一些，能得到更好的结论.为此，先给出若干引理.

引理5A是n阶半正定Hermite矩阵⟺存在半正定Hermite矩阵C，使得A=C2.

证先证必要性.存在酉矩阵U，使得

其中λi是A的特征根，都为实数且λi≥0，i=1,2,…,n.于是

记

则A=C2,C是半正定Hermite矩阵.

从而A是半正定Hermite矩阵.

下面是一个重要的引理.

引理6设A,B为复数域上的m阶矩阵，则AB和BA有完全相同的特征根，且对应特征根的重数也相同.

证考虑矩阵

其中,Im是m阶单位阵.下面我们总假定λ≠0，对等式

两边取行列式，得

同样，对等式

两边取行列式，有

于是，λ≠0时，有det(λ2Im-BA)=det(λ2Im-AB)，即det(tIm-BA)=det(tIm-AB)对任意t>0都成立.从而AB和BA有相同的特征多项式，于是有相同的特征根，且对应特征根的重数也相同.

由上述引理即可证明比定理1和定理2更好的结论.

定理3若A,B都是半正定Hermite矩阵，则AB的所有特征根均为非负实数.

结合定理1和定理3，有

定理4设A和B都是n阶半正定Hermite矩阵，设A的所有特征值为λ1,λ2,…,λn，B的所有特征值为μ1,μ2,…,μn，记

则AB的所有特征值vi都是实数，且|v|∈[m1m2,M1M2]，i=1,2,…,n.

[参考文献]

[1]华罗庚.一个关于行列式的不等式[J].数学学报，1955，5(4):463-470.

[2]许以超.线性代数与矩阵论[M]. 北京：高等教育出版社，2008.

[3]许以超.代数学引论[M].上海：上海科学技术出版社，1983.

[4]张贤科，许甫华.高等代数学[M].北京：清华大学出版社，2004.

TheApplicationsofHuaLoo-KengInequalityintheEstimationofEigenvaluesInvolvingtheProductofHermitianMatrices

ZHONG Wen-ti

(SchoolofMathematicalSciences,SouthChinaNormalUniversity,Guangzhou510631,China)

Abstract:ThispapergivestheestimationoftheeigenvaluesofABwhichA,BareHermitianmatricesbasedonainequalitywhichHuaLoo-Kengprovedinthestudyofthefunctionsofseveralcomplexvariables.

Keywords:Hermitianmatrices;productofmatrices;eigenvalues；estimation

[中图分类号]O151.21

[文献标识码]A

[文章编号]1672-1454(2015)04-0083-04