100m级高面板堆石坝应力变形分析

100 m级高面板堆石坝应力变形分析

陆 静1， 胡仲萍2

(1.杨凌职业技术学院水利工程分院， 陕西 杨凌 712100; 2.渭南市洛惠渠管理局， 陕西 渭南 715100 )

摘要：采用邓肯张E-B非线性弹性模型，利用自动剖分程序建立三维模型，对某100 m级高面板堆石坝进行三维有限元数值模拟计算，并选取合适的反映堆石料流变特性的本构模型分析了坝体的应力变形情况。结果表明:坝体的位移和应力分布规律基本合理，数值大小都在允许的范围内，但在堆石流变作用的影响下，坝体的应力变形明显增大，流变作用对坝体的影响不可忽略，本文为坝体的设计和施工提供支撑。

关键词：面板堆石坝； 本构模型； 应力变形； 流变

收稿日期：2015-03-24

作者简介：陆 静(1987)，女，陕西武功人，硕士，助教，专业教师，主要研究方向：土石坝。

中图分类号：TV641.43

Analysis on Stress and Deformation of 100m High CFRD

LU Jing1, HU Zhong-ping2

(1.Branch College of Hydraulic Engineering, Yangling Vocational and Technical College, Yangling, Shaanxi 712100, China;

2.Luohui Cannel Administration Bureau of Weinan City, Weinan, Shaanxi 715100, China)

Abstract:In order to study the influence of material properties on dam stress and deformation, this paper established three-dimensional solid models by applying Duncan-Chang Model nonlinear elastic model with automatic mesh program, the three-dimensional finite element of a 100m high CFRD was numerically simulated, and appropriate constitutive model that could reflect the rheological characteristics of materials was adopted to analyze the stress and deformation of the dam body. The result shows that dam displacement and distribution of stress is basically reasonable, the numerical values are in a permitted range. But the stress and deformation of dam increases significantly under the influence of rheological effect, which can't be neglected. This paper can be used as a reference for dam body design and construction.

Key words: CFRD; constitutive model; stress and deformation; rheology

面板堆石坝因其安全性好，适应性强而成为一种富有竞争力的坝型。其筑坝材料由上游防渗混凝土面板、垫层料、过渡料和主、次堆石料组成，筑坝堆石的材料特性对坝体的应力变形有直接影响[1]。堆石料是非线性材料，应力变形随荷载的大小而变化，除在外力作用下的瞬时变形，筑坝堆石料的流变特性[2]使得坝体的应力变形随时间的延长而增大，已有研究也表明，堆石料的流变特性对坝体应力变形的影响不可忽视[2~7]。因此堆石料静力本构模型和流变模型对能否合理的模拟坝体的应力变形有重要影响。

目前，邓肯-张模型(Duncan-Chang)简单易于理解并能反映土体变形的主要特点而在工程界和学术界都得到了广泛的应用[2]。基于继效理论的7参数增量流变模型[8]以应力增量的形式推导，考虑了加载应力路径，体现了堆石流变的遗传特性。本文采用邓肯E-B模型和增量流变本构模型模拟了某100 m级高面板堆石坝的的应力变形情况，为坝体的设计和施工提供支撑。

1工程概况

某水库是潇水流域梯级开发的龙头水库，具有灌溉、防洪、下游补水和发电，兼顾航运等综合利用效益的大型水利水电枢纽工程。挡水建筑物混凝土面板堆石坝，最大坝高113 m，坝顶长328 m，上游坝坡为1∶1.4，下游坝坡为1∶1.4，并设置二级宽3 m的马道，马道高程分别为262.00 m、292.00 m。本工程为Ⅰ等大(1)型水利水电枢纽工程，正常蓄水位313.0 m。大坝剖面见图1。

2计算方法及计算参数

2.1　筑坝材料的静力本构模型及参数

(1)堆石料参数。 筑坝材料本构模型参数由长江科学院通过大型三轴试验获取。

(2)流变计算模型参数。堆石料的流变参数主要参照水布垭混凝土面板堆石坝原型观测资料反演分析资料选用，如表2所示。

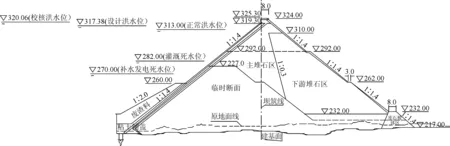
图1　大坝标准横断面图

填料干密度ρd(g/cm3)E-B模型参数φ0△φRfKnKbmKur主堆石2.1552.19.60.8511350.315310.262270次堆石2.1050.99.30.8310230.244590.222046垫层料2.1749.86.60.8812000.375600.322400过渡料2.1548.07.10.8312240.225600.212448

注：φо、Δφ为材料非线性强度参数，由三轴试验确定； K、n分别为切变杨氏模量基数和指数； Rf为破坏比； Kur为回弹模量基数； Kb、m分别为体变模量基数、指数。

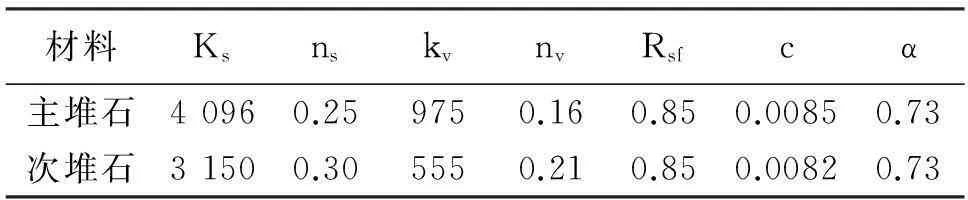
表2 堆石料流变模型参数 [9 ]

注： ks、ns、kv、nv均为模型参数； Rsf为破坏比； c、α均为试验常数。

(3)接触面参数。面板与垫层之间设置采用Goodman无厚度接触面单元模拟两种材料之间的相互作用来解决刚度差异较大的两种材料的位移不协调问题。计算参数见表3。

表3　Clough-Duncan非线性模型(无厚度单元)参数

注： c为粘聚力； d为接触面的内摩擦角； Rf为破坏比； K1、n分别为剪切劲度系数、指数。

(4)线性材料参数。

表4　线弹性材料计算参数

注：ρ为混凝土密度； E为弹性模量； μ为泊松比。

2.2　计算网格的划分

根据坝区地质条件和坝体分区特点，以河床典型剖面为基准，采用三维自动剖分程序剖分坝体单元，沿坝轴线方向共设定42个计算剖面进行剖分，得到整个坝体结构的节点总数8 761个，单元总数7 715个。坐标设定：坝轴向设为z轴向，自上游到下游水平方向为x轴方向，沿高程增加的铅直方向为y轴向。三维网格剖分图如图2所示。同时，为分析二维计算下坝体的应力变形，建立二维有限元计算模型，二维网格节点数314个，单元292个，材料分区、加载过程、筑坝材料参数等均与三维相同。

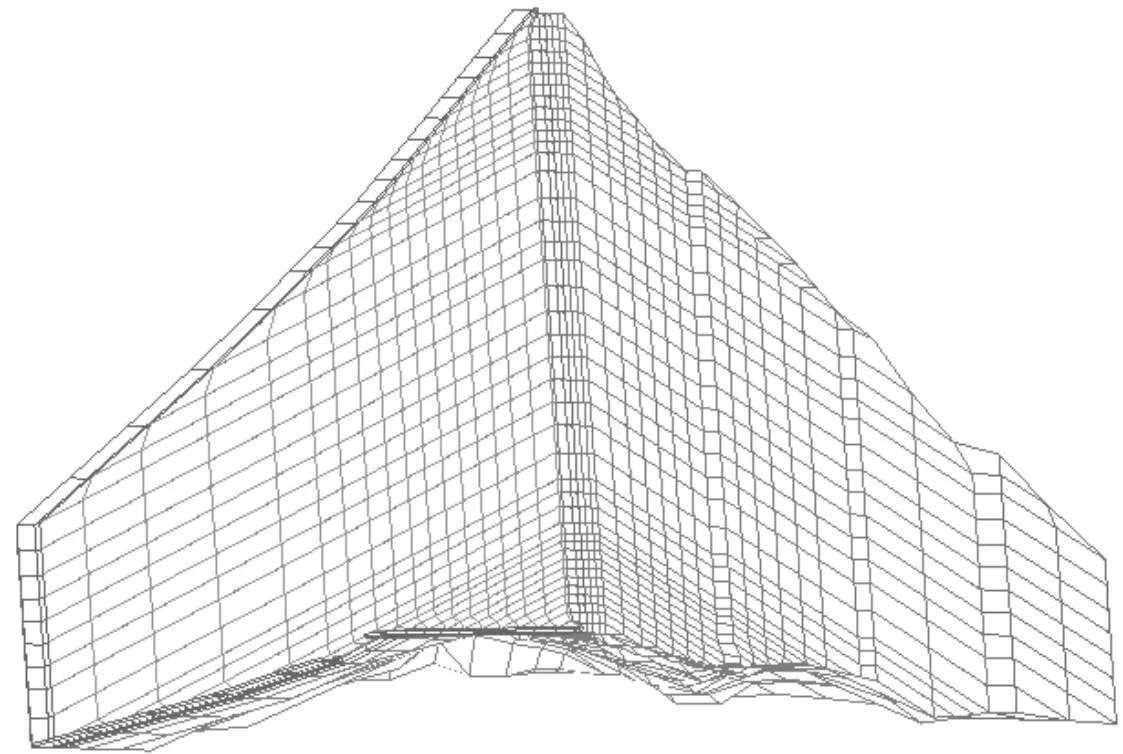
图2　坝体三维网格剖分图

2.3　荷载的分级

考虑到坝体施工分层填筑的特点和堆石体非线性特性，荷载采用逐级施加的方式。按坝体施工填筑高程的先后顺序分26级来模拟，顺序如下：第1～6级：一期堆石体临时断面填筑至275.0 m高程；第7～14级：二期堆石体全断面填筑至292.0 m高程；第15级：一期面板浇筑至285.00 m高程；第16～22级：三期堆石体全断面填筑至320.30 m高程；第23级：水库蓄水至发电死水位270.00 m高程；第24级：水库蓄水至282.00高程；第25级：二期面板浇筑至坝顶320.30 m高程；第26级：模拟水库蓄水至正常蓄水位313.00高程。本次计算采用三维有限元静力计算程序。

3计算结果分析

3.1　二、三维计算坝体应力变形

图3为满蓄期坝体坝轴线位置位移及主应力比较图。二维计算坝体的应力变形均比三维计算的结果要大。二维计算时取坝体标准横断面来进行计算，没有考虑其两侧堆石体对其因摩擦而产生的拱作用，从而计算的坝体变形较大。而三维有限元几何模型考虑了空间拱效应的影响，从而坝体变形较小，更符合实际施工。因此，在下文中，利用三维有限元几何模型模拟堆石的材料特性对坝体的应力变形。

图3满蓄期坝轴线位置位移和主应力

3.2　堆石体的变形与应力

经计算，竣工期，由于堆石体的泊松效应，剖面上下游方向水平位移均指向坝坡外侧，向上游最大位移为20.9 cm，向下游最大位移为23.4 cm。最大竖向位移为71.9 cm，发生在高程265.0 m附近的坝轴线附近。坝体主应力等值线与坝坡基本平行，且从坝顶向坝基呈现逐渐加大的趋势。堆石体第一主应力最大值为1.86 MPa，第三主应力最大值为0.69 MPa，极值位置都位于坝轴线底部的岩基上。

图4为满蓄期堆石体位移和主应力等值线图。图4(a,b)表明，水库蓄水后，在水荷载的作用下，坝体水平位移均有向下游方向变化的趋势。向上游位移的最大值为8.4 cm，向下游位移的最大值为27.0 cm。最大竖向位移为72.7 cm，占坝高的0.64%，位于高程260.0 m附近坝轴线区域。图5(a,b)显示，堆石体大、小主应力等值线在上游堆石区都出现上抬现象，相对竣工期而言，极值量值有所增大，所处的位置进一步向上游主堆石区靠近。第一主应力最大值增大到1.98 MPa，第三主应力最大值增大到0.77 MPa。

图4　满蓄期堆石体位移等值线图((单位：cm)

3.3　面板的变形与应力

图6为满蓄期面板挠度和坝轴向位移等值线图，图7为满蓄期面板顺坡向应力和坝轴向应力等值线图。水库蓄水后，面板变形分布规律较好，面板挠度基本指向坝内，面板中下部约1/2~1/3坝高部位区域数值较大，最大值为22.5 cm。水荷作用使得面板在坝轴线方向由两岸向河谷中央挤压，其中向右岸最大位移为3.9 cm，向左岸最大位移为4.1 cm，极值位置均在280.0 m高程左右(图6(a,b))。面板绝大部分区域表现为受压状态。其中顺坡向压应力最大值为7.07 MPa，顺坡向拉应力最大值为1.36 MPa，位于左、右岸一期面板中下部；坝轴向压应力最大值为2.60 MPa，坝轴向拉应力最大值为0.8 MPa，位于右岸面板位置(图7(a,b))。

图5　满蓄期坝体主应力等值线图(单位：MPa)

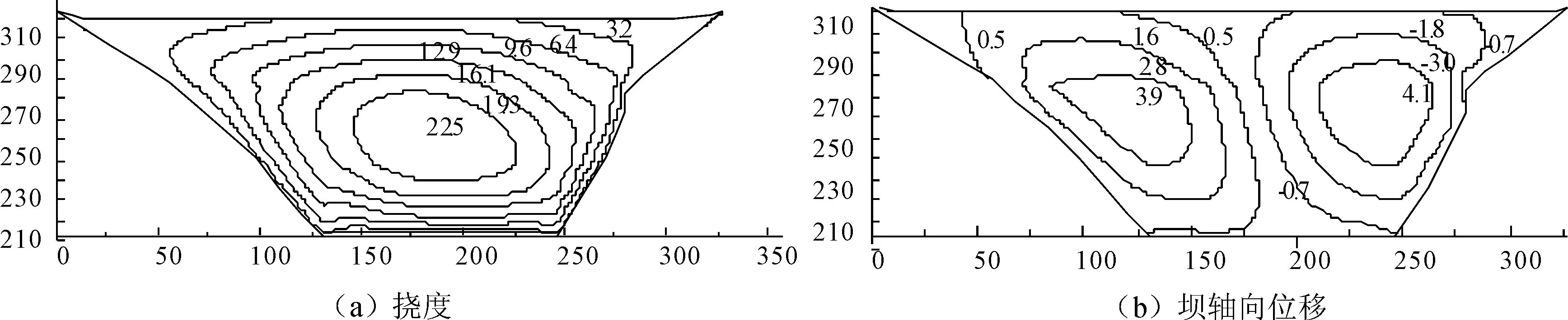
图6　满蓄期面板挠度和坝轴向位移等值线图 (单位：cm)

图7　满蓄期面板顺坡向应力和坝轴向应力等值线图(单位：MPa)

3.4　缝的变形

水库蓄水后，面板的变形增大，各块面板之间设置的竖缝及面板与其底部趾板之间的周边缝的变形也随之产生。缝的变形计算结果：①竖缝的变形：垂直缝长方向的沉降最大为1.9 cm；沿缝长方向的错动位移最大值为2.3 cm；河床部位的竖缝全部呈压紧状态，两岸的面板缝为张拉状态，张开位移最大值为1.9 cm，处于岸坡地形变化较大的位置；压缩位移最大值为1.1 cm，发生在河谷中央剖面的1/2坝体高程处；②周边缝垂直缝长方向的沉降最大值为2.4 cm，周边缝沿缝长方向的错动位移最大值为1.6 cm，周边缝基本处于拉伸状态，最大张拉量为1.0 cm，发生在右岸岸坡地形变化较大的位置。

3.5　流变作用下坝体应力与变形

通过计算，堆石体流变作用对坝体及面板的应力及变形分布规律没有影响，考虑堆石流变后，坝体及面板的应力变形均有所增大。考虑堆石流变作用后，坝体最大竖向位移为80.2 cm，占轴线坝高的百分比为0.7%，增大了9%；上、下游方向水平位移分别增大为11.0 cm、37.2 cm，涨幅为 31%和38%；坝体的主应力变化不大，第一、第三主应力分别增大为2.0 MPa、0.92 MPa；面板的挠度值增幅不大，仅为1.0 cm，但河床部位的面板进一步压紧，面板压应力明显提高，面板顺坡向压应力为7.76 MPa，增加了0.7 MPa，坝轴向压应力也增加了0.2 MPa，面板在两岸连接处的拉应力也有所增加；面板与趾板之间周边缝的变形也增加明显，缝的错动及张拉趋势进一步增大，其在垂直缝长方向的错动为2.0 cm，张拉量为2.1 cm，分别增加了0.4 cm 、1.1 cm。

4结语

(1)通过模拟大坝的实际施工、蓄水以及地形等条件，计算得出该面板坝的位移和应力分布规律符合面板坝的应力变形分布规律，竖缝，周边缝的变形也在可控的范围内；建议适当提高280 m高程以下堆石区的填筑指标，提高其变形模量，减小拱效应对面板变形与应力的不利影响。

(2)堆石流变作用使得堆石体的应力变形进一步增大，面板受压状态加剧，在设计时应充分考虑堆石流变作用。

参考文献：

[1]郦能惠,孙大伟,李登华,等.300 m级超高面板堆石坝变形规律研究[J].岩土工程学报,2009,31(2):0155-0160.

[2]钱家欢，殷宗泽.土工原理[M].北京：中国水利出版社，1996.

[3]沈珠江.鲁布革心墙堆石坝变形的反馈分析[J].岩土工程学报,1994, 16(3)：1-13.

[4]沈珠江.土石料的流变模型及其应用[J].水利水运科学研究,1994,12(4)：335-342.

[5]沈珠江,赵魁芝.堆石坝流变变形的反馈分析[J].水利学报,1998,6(6)：1-6.

[6]王 勇,殷宗泽.一个用于面板坝流变分析的堆石流变模型[J].岩土力学,2000,21(3)：227-230.

[7]王 勇,殷宗泽.面板坝中堆石流变对面板应力变形的影响分析[J].河海大学学报,2000,28(6)：60-65.

[8]朱 晟,王永明,徐骞.粗粒筑坝材料的增量流变模型[J].岩土力学,2011,32(11)：3201-320

[9]朱 晟,水布垭面板堆石坝施工与运行性状反演研究[J].岩石力学与工程学报,2011,30(S2):3689-3695.