基于遗传算法的集装箱港口堆场空间动态分配策略
盛 扬,梁承姬,丁 一
(上海海事大学 物流研究中心,上海201306)
0 引 言
目前港口采用的堆存模式有两种:①进、出口箱分开堆放的模式,一般在堆场用地不紧张时采用,以避免进出口箱同时作业时产生相互干扰;②进出口箱混合堆放的模式,当集装箱货运量较大、堆场空间有限时,为顺利完成进出口箱作业才采用。
随着进出口箱混合堆存模式的兴起,该模式下堆场空间分配问题的研究也在不断发展,需要同时考虑进口箱和出口箱的堆存要求。Liang等[1]提出了自动化码头堆场空间分配的通用模板,并使用Cplex求解了模型,文中研究的堆场箱区是允许AGV 小车行驶到箱区两侧进行作业的;Wiese等[2]提出了一个关于堆场布局的整数线性规划问题,研究了平行分布和垂直分布的箱区布局的运输通道对空间分配问题的影响,并提出一种启发式算法求解该问题;Bazzazi等[3]提出利用遗传算法解决进口箱的堆场空间分配;范佳静[4]提出了必须将集装箱箱区贝位作业平衡率及集卡在泊位与箱区贝位运输距离这两个矛盾目标置于同一个目标函数,并构建了相应的非线性整数规划模型;毛钧等[5]分析了影响集装箱码头堆场空间资源配置优化的主要因素,提出混堆模式下集装箱码头堆场空间资源配置优化的两阶段优化思路。分别以平衡各箱区贝位间的作业量和最小化泊位到堆场的运输距离为两个阶段的优化目标,构建两阶段优化模型;Lu等[6]提出了一种混合整数规划的模型来求解集成泊位和堆场计划的模板,考虑了操作成本和运输路线的长度,并用启发式算法求解大规模的问题;Byung等[7]提出了两种码头的布局,一种是平行于岸边的布局,另一种是垂直于岸边的布局,并通过分析成本因素来优化码头布局;陶经辉等[8]建立了二阶段式的进出口箱堆存分配模型,第一阶段解决工作量平衡优化问题,第二阶段解决箱组平衡优化问题。模型采用启发式算法求解;陈宇等[9,10]提出了集装箱港口基于作业路的堆场空间分配问题,建立了堆场空间分配的静态和动态模型,并使用Lingo进行求解。
上述文献没有使用遗传算法求解同时考虑进出口箱的动态分配问题,因此本文提出混堆模式下堆场空间动态分配的模型,并提出一种遗传算法来解决问题,并和文献[9]中的Lingo方法求解的结果进行比较。
1 问题描述
堆场空间动态分配问题是指为随机进入堆场的进出口箱分配堆存空间。所谓 “动态”是指各箱区因完成装船、卸船、提货、进场作业可用空间在不断发生变化。因此,堆场空间的动态分配是一个复杂的过程。就以往对堆场空间动态分配问题的研究来看:方法上多以滚动计划法为主,要求制定堆场分配计划时不仅要考虑当天的进场箱,更要考虑未来几天堆场内集装箱的进出情况。一般,滚动式堆场计划都以3天为决策周期,每天分成3-4个阶段且只有第1天第1阶段的计划会被执行。执行完毕后,更新堆场信息、决策周期向前推进一个阶段,进行下一轮的决策。
本文对堆场上的集装箱按作业状态分为4 类,如图1所示。其中,D 箱和G 箱是研究重点。在本文中,D 箱和G 箱的堆存计划均考虑了 “作业路”的影响且是阶段性制定,即当前时段提前做好下一时段的D 箱和G 箱的堆存计划。

图1 集装箱分类
随着集装箱货运量的不断增加、船只形体的不断扩大,为船舶开通的各作业路的任务量也在不断增加,因此堆存策略需要避免集装箱在堆场堆放得过于分散或过于集中。本文的堆场计划主要考虑多条船舶多条作业路的堆场分配,令同一船舶的不同作业路的集装箱堆放在不同箱区,并且让船舶堆存的箱区保持 “既集中又分散”,这样可以避免装卸的集卡过于拥挤,又避免太分散而消耗成本。本文已知的输入参数包括各船舶各阶段各装卸作业路的任务量,各阶段各箱区的可用容量和各阶段离开各箱区的集装箱量等等。通过这些已知参数来决策各阶段的船舶上的每一作业路的集装箱堆存在各箱区的集装箱量。
2 堆场空间动态分配模型
本文将建立基于每艘船每条装卸作业路任务量已知的堆场空间动态分配模型。本模型适用于船体较大、卸货量较多的船舶。对卸载进口箱:先从已定的作业路调度方案中得到该船各计划时段各作业路进口箱的任务量,然后根据其和船开通的作业路总数制定进口箱的堆存计划。对进场的出口箱:根据各计划时段开始前箱区的容量情况制定基于作业路数的堆存计划。模型意在实现集卡在泊位-箱区间运输总距离最小、集装箱的合理分散和不同船不同作业路进口箱错开堆放在不同箱区。
2.1 相关假设
(1)已知进港船舶预靠的泊位和开通的作业路数;
(2)已知船舶各作业路各计划时段要完成的进口箱量和进场的出口箱量;
(3)决策期内计划时段t进场或卸载的集装箱均在该时段完成堆存作业;
(4)堆场内有足够的集卡和场桥,且每次只处理一个集装箱;
(5)所有集装箱不分类型,统一尺寸定为20寸。
2.2 模型参数
T:1个决策周期包含的计划时段数;决策周期为1天,每8个小时为一计划时段,T=3,每个计划时段用t表示,每次只有t=1的决策被执行。
B:堆场箱区数。
S:决策周期内要卸货的船数。
V:决策周期内进场的出口箱所属的船数。
P:卸货船分配的岸桥数,即作业路数。
M:一个给定的大数。
Capacityi:箱区i的可用容量,本问题取600。
Initiali0:箱区i的初始库存。
Invenit:计划时段t开始时刻箱区i的库存量。
Mit:决策周期开始前已卸载至箱区i将在计划时段t提走的进口箱量。
Nit:决策周期开始前已堆存在箱区i并在计划时段t装船的出口箱量。
Pickit:计划时段t,将从箱区i提走的进口箱量。
Loadit:计划时段t,将从箱区i装船的出口箱量。
Workloadit:计划时段t,箱区i的装卸工作量。
distance1ij:箱区i与船舶j 的距离。
distance2il:箱区i与船舶l的距离。
Dijt:计划时段t从船舶j 卸载至箱区i的进口箱量。
Gilt:计划时段t进场至箱区i船舶l的出口箱量。
Ditk:计划时段t卸船至箱区i,计划时段k提走的进口箱量。
Gitk:计划时段t进场至箱区i,计划时段k装船的出口箱量。
getlt:计划时段t进场,决策期外装船的船舶l的出口箱量。
E2lt:计划时段t进场,船舶l的出口箱堆存的最大箱区数。
Gltk:计划时段t进场,计划时段k 装上船舶l 的出口箱量。
Djrtk:计划时段t从船舶j 第r 条作业路卸载,计划时段k被提走的进口箱量。
Dijrt:计划时段t从船舶j 第r 条作业路卸载至箱区i的进口箱量。
dischargejrt:计划时段t从船舶j 第r 条作业路卸载,决策期外被提走的进口箱量。
E1jrt:计划时段t靠港,船舶j第r 条作业路卸载的进口箱堆存的最大箱区数。
决策变量:
Dijrtk:计划时段t从船舶j第r条作业路卸载至箱区i,计划时段k被提走的进口箱量。
Giltk:计划时段t进场至箱区i,计划时段k装上船舶l的出口箱量。
aijrt:计划时段t从船舶j 第r 条作业路卸载至箱区i,决策期外被提走的进口箱量。
bilt:计划时段t进场至箱区i,决策期外装船的船舶l的出口箱量。
S1ijrt=1,箱区i堆存了计划时段t从船舶j第r条作业路卸载的进口箱,反之为0。
S2ilt=1,箱区i堆存了计划时段t进场的船舶l 的出口箱,反之为0。
(其中i=1,2…B;j=1,2…S;l=1,2…V;r=1,2…P;t=1,2...T;k>=t)。
2.3 目标函数及约束条件
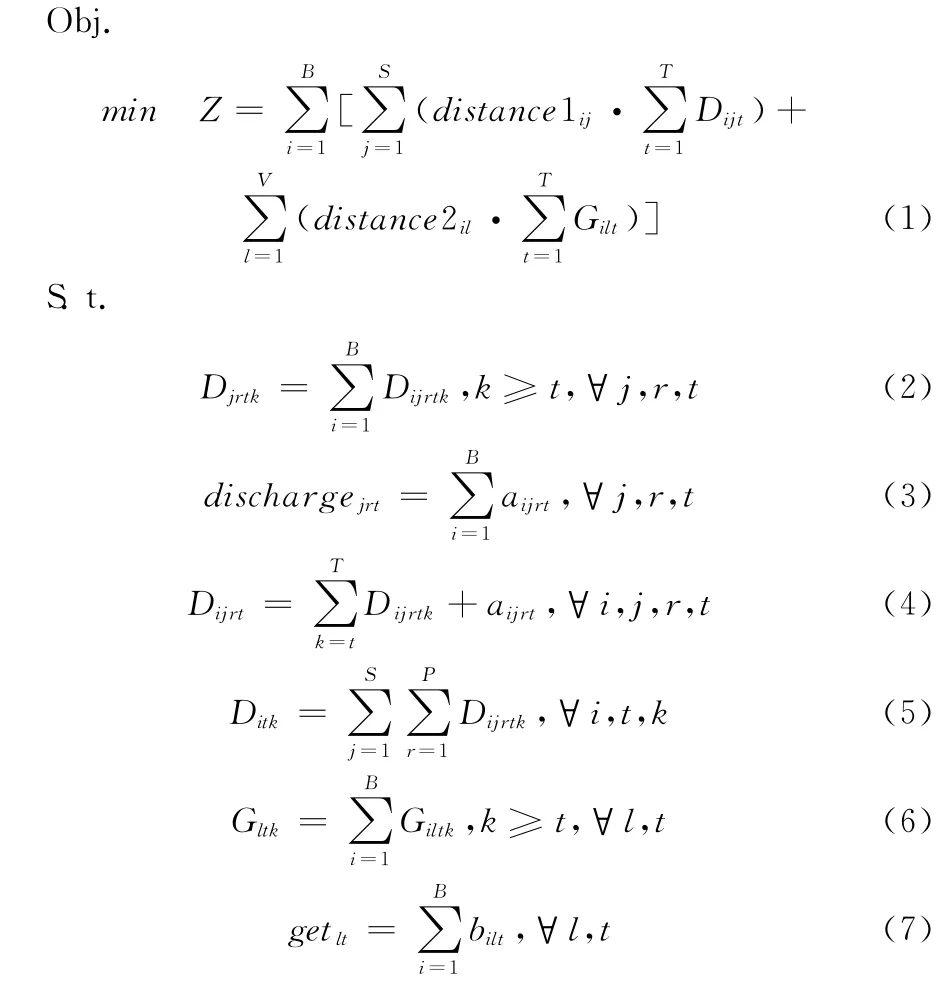
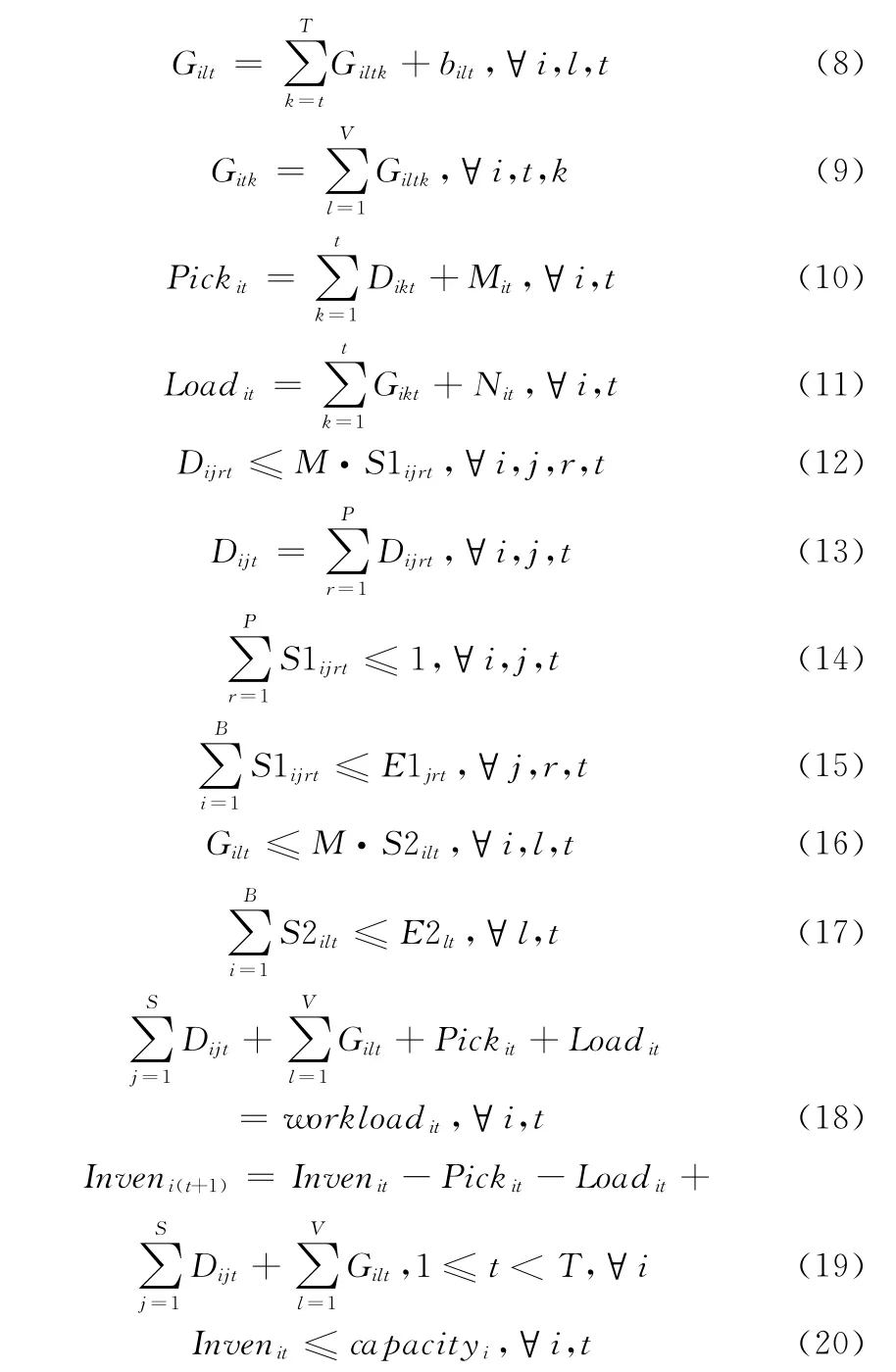
其中,S1irjt,S2ilt为0、1变量,Dijrt,Gilt,Pickit,Loadit为非负整数。
式 (1)表示模型目标是所有计划时段,集卡在泊位-堆存箱区间运输卸船进口箱和装船出口箱的总距离最小。
式 (2)表示计划时段t船舶j 第r 条作业路卸载的将在计划时段k 提走的进口箱量等于该时段分配到各堆存箱区的箱量之和。式 (3)表示计划时段t船舶j 第r 条作业卸载的决策期外提走的进口箱量等于该时段分配到各堆存箱区的箱量之和。式 (4)表示计划时段t箱区i 堆放的船舶j 第r 条作业路卸载的进口箱量等于该时段船舶j 第r 条作业路卸载的决策期内和决策期外会提走的进口箱量之和。式 (5)表示计划时段t箱区i 堆放的将在计划时段k 提走的进口箱量等于每条船舶每条作业路卸载至箱区i 的该类进口箱量之和。
式(12)是判断箱区i是否在计划时段t 堆放了船舶j第r 条作业路卸载的进口箱,若堆存了则为1,否则为0。式(13)表示箱区i堆放的船舶j 计划时段t卸载的进口箱量等于船舶j 在该时段所有作业路卸载至该箱区的进口箱量之和。式 (14)表示计划时段t箱区i 只能堆放船舶j 一条作业路或不堆放船舶j 任何作业路卸载的进口箱。式(15)表示计划时段t船舶j 第r 条作业路卸载的进口箱所堆存的箱区总数不大于堆场为船舶j 第r 条作业路分配的最多堆存箱区数。
3 遗传算法的实现
本文采用矩阵式编码方式的遗传算法对模型进行求解,这样可以有效地表示出各时段每艘船舶堆存到各堆场箱区的集装箱量。
3.1 染色体设计
3.1.1 编码
构建一个 (TR×B)的矩阵,TR 表示计划时段数T乘以作业路数R 的数量,B 表示箱区数量。染色体中的每个基因表示的是每个时段内船舶每一作业路存放在各个箱区的集装箱数量。每一行的基因之和为某一船舶某一时段内某一作业路上存放到堆场的集装箱总和。而每个箱区堆存的集装箱量不能超出每个时段内每个箱区的可用容量。
表1与表2分别表示各阶段作业路的任务量及箱区容量的变化量,表3为某一艘船,2条作业路上的集装箱堆存到3个箱区的染色体编码 (灰色为箱区的可用容量)。
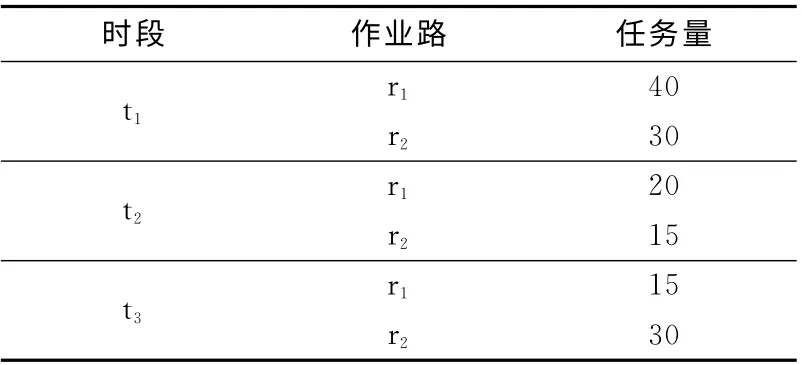
表1 各阶段作业路任务量

表2 箱区容量变化
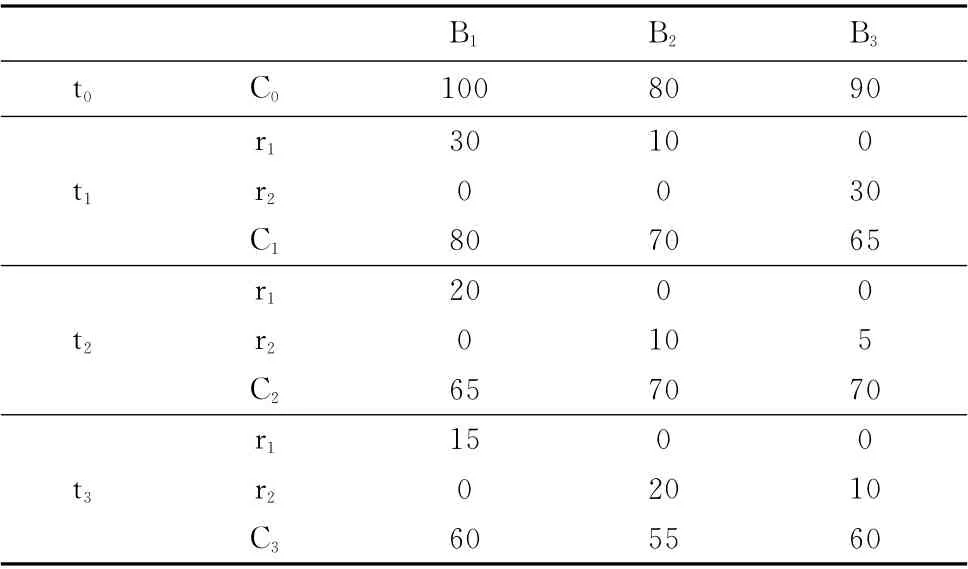
表3 染色体编码
3.1.2 生成初始种群
初始种群的结构对于遗传算法的计算效率有着重要的作用。为了随机生成初始方案,本文主要分为以下几个步骤:
步骤1 先生成第i行的基因,在第j列中,根据该时段船舶作业路是否有集装箱需要分配,判断在第i行即第i个时段船舶是否分配集装箱给该箱区,若满足条件,则进入步骤2,若不满足条件,则在这个基因位置生成0,然后判断j+1列;
步骤2 根据第i个时段箱区被提走或装船的集装箱量ai更新箱区可用容量,直到i的值大于T 为止。判断箱区可用容量是否大于0,若满足条件,则进如步骤3,若不满足,则令该基因值为0,进入第j+1列;
步骤3 在该基因位置随机生成 [0,4*Sij/B]区间内的整数,判断该基因值是否小于C,若满足条件,则更新该时段船舶j的作业路r 完成的集装箱量c,更新箱区可用容量C,并进入第j+1列;若不满足,则令该基因值等于C,更新c和C,Sij为船舶的作业路在第i时段需要卸载/装船的集装箱量,B 为箱区总数;
步骤4 重复步骤2,直到c>Sij或j=B 时则调整此次基因位置的基因值,使得c=Sij,更新箱区可用容量C,令第i行第j+1列至第B 列位置的基因值都为0;
步骤5 然后开始生成第i+1行的基因,重复步骤1~步骤4;
步骤6 当一个个体中的所有基因都生成完毕,开始生成下一个个体,直到种群规模达到M,则终止初始解的生成。(其中i=1,2…TR;j=1,2…B)。
3.2 交叉操作
保持新一代种群的优秀个体的适应度是非常重要的,因此本文提出了最常用也是最简单的交叉方法——单点交叉法。首先随机生成一个规模为M 的序列,根据生成的序列,把序列中相邻的编号个体进行两两交叉,具体操作如图2所示。
3.3 变异操作
当满足变异条件时,将染色体第i行中随机两列的基因值互换。
3.4 染色体修复
由于本文染色体编码的特殊性,交叉变异后需要进行修复,具体步骤如下:
步骤1 先判断各箱区是否只堆放船舶的一条作业路或不堆放船舶任一条作业路的集装箱,若满足条件,则到步骤2,反之,则令该箱区中船舶所有作业路r中除最大基因值以外的其它基因值随机分配到其它堆存的箱区,并到步骤2;
步骤2 对染色体中第i行的基因求和,若基因之和与船舶作业路在该时段卸载或装船的集装箱量的差值小于0,则到步骤3,反之,则到步骤4;

图2 交叉操作
步骤3 找到加上了差值后基因之和依然不超过船舶作业路在该时段卸载或装船的集装箱量的第j列,该位置的基因值加上差值;若无法满足该条件,则使得第i行中基因值最小的那一列基因值加上0至差值之间随机生成的整数,直到满足该条件为止,更新差值,重复步骤3,直到差值为0。到步骤4;
步骤4 找到减去差值后基因之和仍不少于0 的第j列,该位置的基因值减去差值。若无法满足该条件,则使得第i行中基因值最大的那一列基因值减去0 至差值之间随机生成的整数,直到满足该条件为止,更新差值,重复步骤4,直到差值为0。到步骤5;
步骤5 对染色体中每个时段每个箱区堆存的集装箱量求和,若和超过该时段该箱区可用容量,则到步骤6,若和小于第i时段该箱区可用容量,结束修复;
步骤6 找到超出箱区可用容量的第j列,找出该时段中最大的基因值所在行,将该基因值减去差值,并将该行其它列中的最小基因值加上差值,到步骤5。
3.5 选择策略和结束规则
采用轮盘赌方式产生与种群相同数量的染色体即为下一代。如果迭代到最大一代,则停止;否则进入3.2节。
4 算例与结果分析
在一台装有Intel双核P8600@2.6GHz处理器和2GB内存的个人电脑上用Matlab运行本文提出的GA 方法来求解算例。数据规模为:船舶数量为10条船,装卸作业路数量为36条,其中4条船有出口箱任务,箱区数量为9,设置种群规模为150,迭代次数为500,对不同计划时段进场的出口箱、卸载的进口箱完成了堆场空间安排,运算20次得到的平均最优值为290 638m。t=1时的堆场箱区分配结果如图3所示,箱区堆存的集装箱量如表4所示,GA 的收敛结果如图4所示。

图3 计划时段t=1时堆场箱区分配

表4 t=1时堆场箱区堆存集装箱数量

图4 GA 的收敛结果
文献 [9]中的Lingo方法对相同算例运算得出的最优值为280846m,GA 与Lingo求解误差为3.5%。通过对不同规模数据的案例采取GA 与Lingo进行比较,得出的计算时间和目标函数值如表5所示。可以看到两种方法在小规模数据上的计算时间和目标函数相差不大,但是在较大规模的数据上,Lingo的表现则不如GA,并且Lingo无法求解较大规模的数据。

表5 不同案例的Lingo和GA 结果的比较
5 结束语
本文提出了一个基于已知各作业路任务量的集装箱堆场空间动态分配模型,使用GA 算法对模型进行求解,并针对不同数据规模的案例采取GA 和文献 [9]中的Lingo方法进行比较,结果发现GA 在较大规模数据上有较好的表现,并且在同等规模数据的结果比较上平均有3%左右的误差。研究发现,本文提出的GA 算法可以有效地帮助作业量较大的集装箱港口改善堆场空间分配问题。
[1]Liang Pingku,Loo Hay Lee,Ek Peng Chew,et al.An optimisation framework for yard planning in a container terminal:Case with automated rail-mounted gantry cranes[J].OR Spectrum,2010,32 (3):519-541.
[2]Jrg Wiese,Leena Suhl, Natalia Kliewer. Mathematical models and solution methods for optimal container terminal yard layouts[J].OR Spectrum,2010,32 (3):427-452.
[3]Bazzazi M,Safaei N,Javadian N.A genetic algorithm to solve the storage space allocation problem in a container terminal[J].Computers &Industrial Engineering,2009,56 (1):44-52.
[4]FAN Jiajing.Space allocation for container terminal based on mixed storage model [J].Journal of Zhejiang University of Science and Technology,2013,25 (3):168-175 (in Chinese).[范佳静.基于混堆模式的集装箱堆场空间分配研究 [J].浙江科技学院学报,2013,25 (3):168-175.]
[5]MAO Jun,LI Na,JIN Zhihong.Optimization of the allocation of space resources in a container terminal based on mixed stacking pattern [J].Journal of Dalian Maritime University,2014,40 (1):117-122 (in Chinese).[毛钧,李娜,靳志宏.基于混堆模式的集装箱码头堆场空间资源配置优化 [J].大连海事大学学报,2014,40 (1):117-122.]
[6]Lu Zhen,Ek Peng Chew,Loo Hay Lee.An integrated model for berth template and yard template planning in transshipment hubs[J].Transportation Science,2011,45 (4):483-504.
[7]Byung Kwon Lee,Kap Hwan Kim.Optimizing the yard layout in container terminals [J].OR Spectrum,2013,35 (2):363-398.
[8]TAO Jinghui,WANG Min.Assign problem of container yard section based on mixed storage model[J].Systems Engineering-Theory & Practice,2009,29 (8):185-192 (in Chinese).[陶经辉,汪敏.基于混堆模式的集装箱堆场区段分配[J].系统工程与理论,2009,29 (8):185-192.]
[9]CHEN Yu,LIANG Chengji.A strategy for storage space allocation in container terminal based on QCs lines[D].Shanghai:Shanghai Maritime University,2010 (in Chinese).[陈宇,梁承姬.集装箱港口基于作业路的堆场空间分配策略研究 [D].上海:上海海事大学,2010.]
[10]Liang Chengji,Chen Yu.A Yard storage strategy based on QC operating lines[C]//Proceedings of The Fourth International Conference on Management Science and Engineering Management,2010:15-17.

