长输管道埋地弯头结构的复杂应力分析*

夏梦莹，张 宏，刘啸奔，吴经天

（1.中国石油大学（北京）机械与储运工程学院，北京102249；2.中石化天津液化天然气有限责任公司，天津300457）

长输管道埋地弯头结构的复杂应力分析*

夏梦莹1，张 宏1，刘啸奔1，吴经天2

（1.中国石油大学（北京）机械与储运工程学院，北京102249；2.中石化天津液化天然气有限责任公司，天津300457）

基于非线性有限元法，建立了埋地弯头应力计算的数值分析模型。模型中采用非线性土弹簧模拟土壤对管道的约束作用，采用壳单元模拟管道。以管道内压与温度荷载为载荷条件，分析了管道直径、壁厚、弯头曲率半径与夹角、土弹簧抗力多种特性参数对管道应力的影响，得到了管道最大应力的变化规律。计算结果表明，该方法能够较好地模拟弯头的受力过程，可为埋地弯头的设计与安全评价提供一定的参考依据。

焊管；埋地弯头；管土相互作用；非线性土弹簧；应力分析；有限元方法

油气管道是油气输送的主要手段，近年来，我国油气需求快速增长，促进了油气管道建设的快速发展。埋地弯头作为管道的一种常用结构，应用广泛。其受力形式复杂，现有的针对弯头强度的研究中，主要分为两类，第一类为崔孝秉[1]、梁政[2]、邓道明[3]等多位学者给出的弯头强度计算的解析方法，其中崔孝秉提出的弹性抗弯铰法被多个规范引用。第二类为基于有限元的数值模拟方法，近年来陈钢[4]、刘桢彬[5]、张鹏[6]等学者基于该方法开展了弯头强度的应力分析。有限元方法能够更加准确地描述管道的荷载形式与应力分析结果，且随着数值技术的发展，有限元方式的实现也变得普遍化。

本研究基于非线性有限元法建立了长输管道应力分析数值模拟。模型使用离散非线性土弹簧模拟土壤对管道的约束作用，使用壳单元模拟管道。施加内压与温度载荷，分析了土壤特性、管土摩擦系数、管道与弯头尺寸结构对最大应力的影响。为长输管道埋地弯头的设计与强度分析提供了一定的参考。

1 数值模型

1.1 管土相互作用模型

工程中通常采用土弹簧的方法来描述土壤对管道的约束作用，其中Peng L C[7-8]方法应用较为广泛，通用管道应力分析软件CAESARII[9-10]也采用了这种方法。其中土壤约束被描述为管道轴向和侧向的土弹簧，土弹簧存在弹塑性本构，其主要参数为轴向与侧向的极限抗力及轴向与侧向的屈服位移。相关参数计算方法如下。

（1）轴向极限抗力

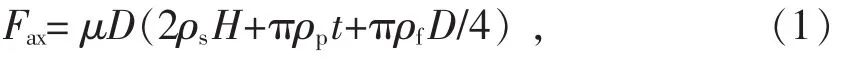
式中：Fax—轴向极限抗力，N/m；

D—管道直径，m；

μ—土壤摩擦系数，其参考值分别为泥沙0.4，沙土0.5，砂砾0.6，黏土0.7；

H—地面至管顶的埋深，m；

ρs—土壤密度， N/m3；

ρp—管子密度， N/m3；

ρf—管内流体密度，N/m3。

（2）侧向极限抗力

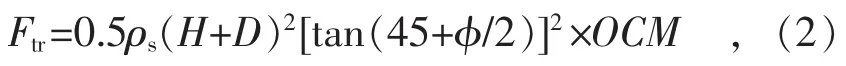
式中：Ftr—侧向极限抗力，N/m；

OCM—回填夯实系数，范围1～8变化；

φ—土壤的内摩擦角。

（3）土壤屈服位移

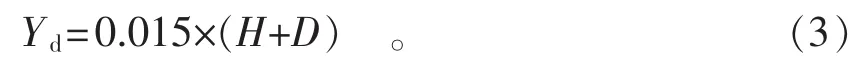
1.2 有限元模型

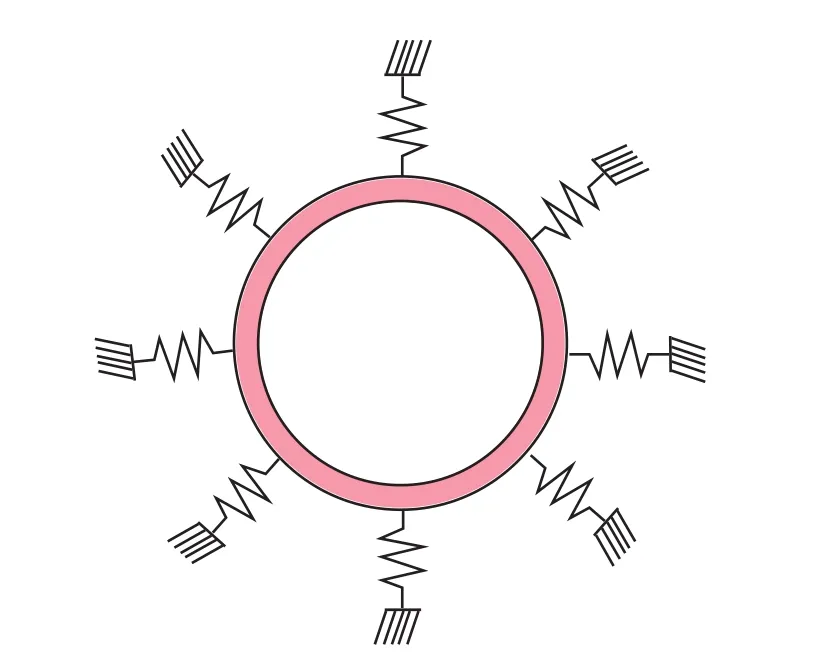
图1 管体横向土弹簧约束示意图

管道埋地会受到土壤对其的约束，管道横向土弹簧约束如图1所示。对长输管道而言，L型弯头结构最为常见。本研究以L型弯头结构为研究对象，不考虑固支墩的影响。L型弯头典型的弯头结构包括两侧直管段和弯曲段一共三部分，如图2所示，管道几何参数包括管道两端直管段长度L1与L2，弯头的曲率半径R与弯头夹角θ，管道的直径D与壁厚t。

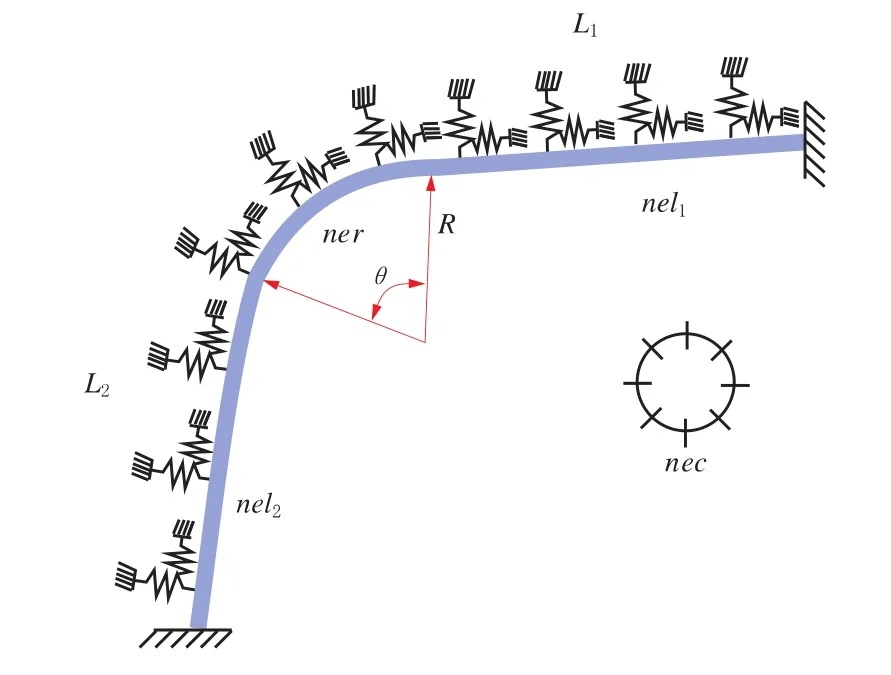
图2 埋地弯头有限元模型示意图

使用ANSYS软件建立有限元计算模型，管道使用四节点壳单元SHELL181模拟，横向与轴向土弹簧分别使用非线性单元COMBIN39模拟。其中管道在环向划分为24(nec)个单元。两端直管段管道轴向0.5 m一个单元 (即nel2=2L2，nel1=2L1)，弯管段管道轴向40(ner)个单元。

建立模型时，首先生成管道节点与管道模型，然后拷贝两倍的管道节点生成土壤节点，最后使用COMBIN39单元连接土壤与管道节点模拟管土作用。在添加边界条件时，对所有土壤节点全约束，对管道只约束管道两端的轴向位移。约束添加后，对管道施加载荷以分析其应力响应。

1.3 管材模型

使用非线性模型描述管材应力应变关系，本研究以X70管材为例进行研究。材料参数选自GB 50470—2008《油气管道抗震设计规范》[11]，弹性模量为2.1×105MPa，屈服强度为498 MPa，抗拉强度为565MPa，抗拉强度对应的极限应变为3%。

2 结果分析与讨论

根据X70管道常用工程参数，选取不同工况进行管道应力分析，参数须考虑管道尺寸、结构、土壤性质、工作载荷四大类。工况计算时以参数基准值作为基本工况参数，在一定取值范围内，变化相应参数来分析管道应力。本案例分析的基本工况参数为：管道直径813.3 mm，壁厚12 mm，工作温差40℃，内压8 MPa，管道中心线埋深1.8 m，土壤的内摩擦角35°，计算可得土壤轴向极限抗力45 kN/m，土壤侧向极限抗力428.7 kN/m。计算模型不考虑固定墩的影响，当两端直管段足够长时，在外载荷作用下弯头会形成自然锚固。经过试算当L1=L2=40 m时，模型能满足本研究计算要求。

基本工况参数下90°埋地弯头的应力与位移响应结果如图3所示。由图3可以看出，弯头受两端直管段的轴向推力作用，使弯头中心所受弯矩较大而产生了较大应力与位移，由图3可以得到最大Mises等效应力为317MPa，最大位移为0.0322m。

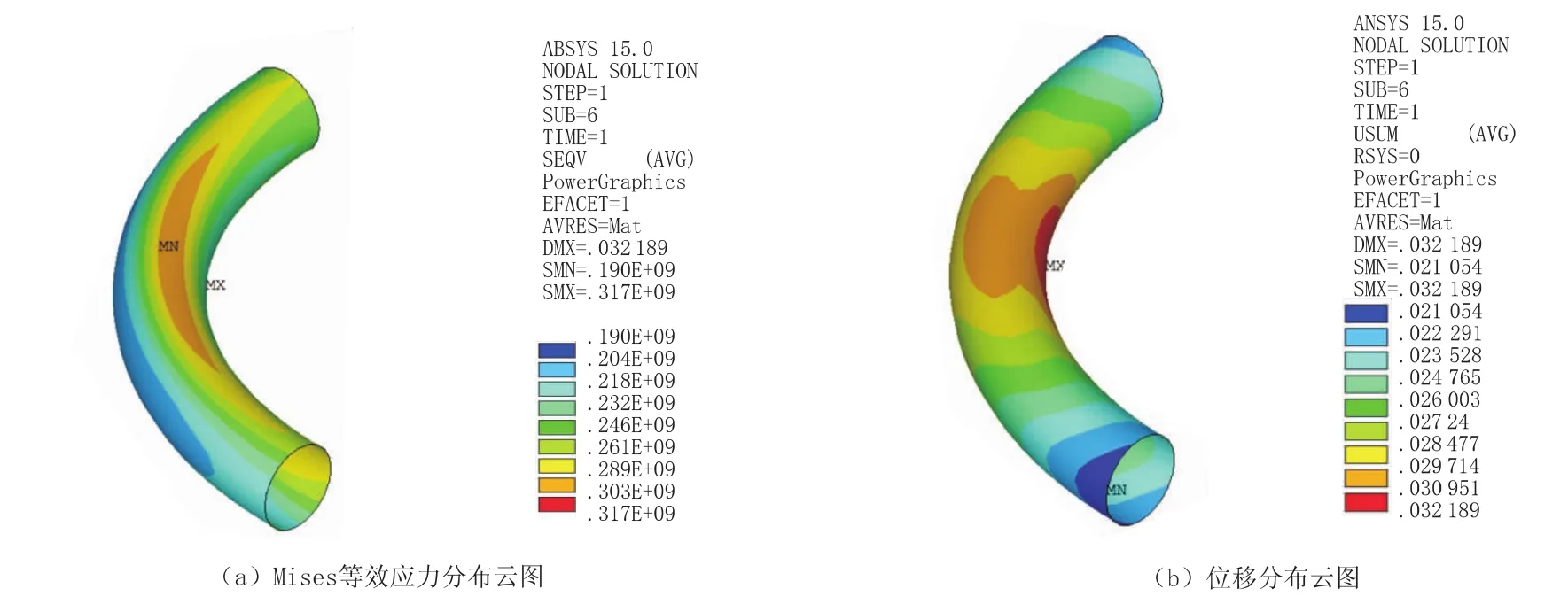
图3 基本工况参数下90°弯头的应力与位移响应结果

本研究采用因素轮换法对各参数进行敏感性分析，方便对计算得到的结果进行分析比较。

2.1 管道几何参数的影响

不同直径与壁厚下弯头最大Mises应力的变化规律如图4所示。计算参数选取工程常用参数，直径包括611 mm，711 mm，813 mm，914.4 mm和1 016 mm五种，壁厚根据不同直径选取。由图4可以看出，随着壁厚的增加弯头内部应力减小，而当壁厚大小相近时，直径越大，弯头应力越大。由此可见，大直径弯头在工作载荷下其Mises应力较大，需要更加关注。

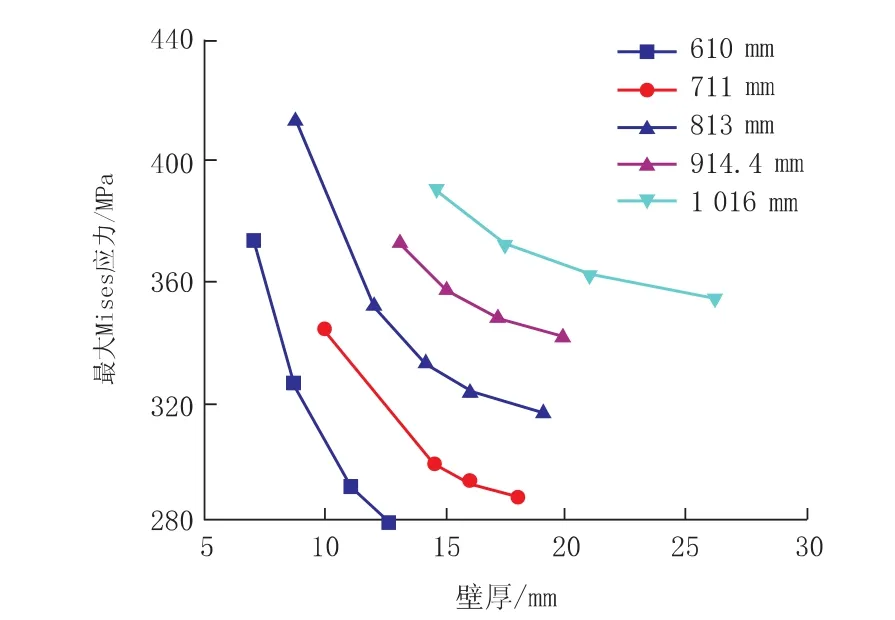
图4 管道最大Mises应力随直径与壁厚的变化曲线

2.2 弯头结构的影响

弯头结构参数包括弯头的曲率半径与弯头夹角。不同弯头曲率半径与弯头夹角下，弯头Mises应力的变化规律如图5所示。图5中曲率半径取值5D～9D，弯头夹角取值从30°到90°。由图5可见，任意弯头曲率半径下，弯头夹角越小，弯头最大Mises应力最大。当弯头夹角介于30°与75°之间时，弯头最大Mises应力随着弯头曲率半径的增大一直减小。当管道夹角为90°，弯头最大Mises应力随弯头曲率半径的增大而减小，当曲率半径达到7D后便基本不再变化。

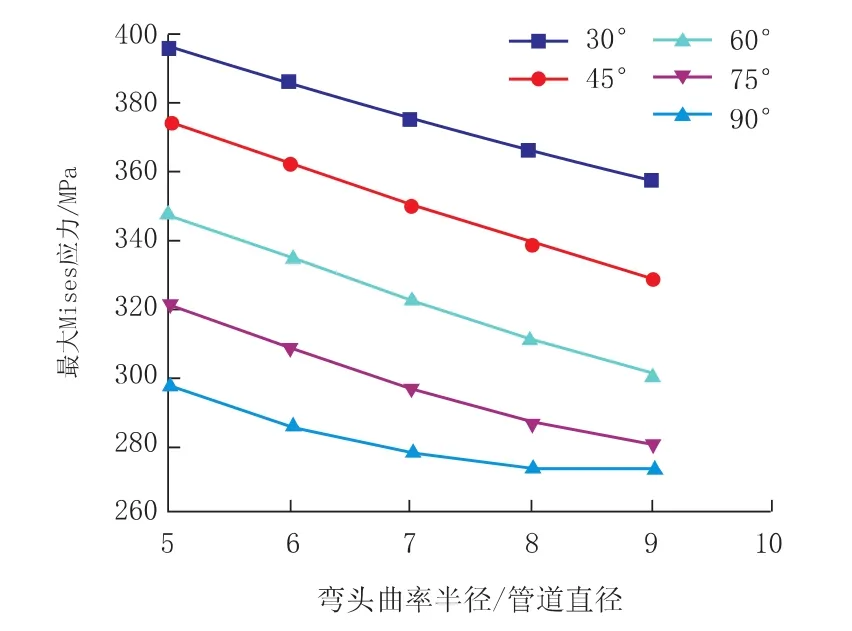
图5 管道最大Mises应力随弯头曲率半径与弯头夹角的变化曲线

2.3 土壤特性的影响

本研究中使用土弹簧模型描述土壤的约束关系，当埋深和管道直径一定后，屈服位移为一个定值，所以这里主要考虑土壤极限抗力的影响。不同轴向土弹簧极限抗力下弯头内最大Mises应力值随侧向土弹簧极限抗力的变化规律如图6所示。由图6可见，当轴向极限抗力较小时（30 kN/m，45 kN/m），弯头最大Mises应力随侧向极限抗力的增大而明显较小；而当轴向极限抗力较大时（60 kN/m，75 kN/m），弯头最大Mises应力随侧向极限抗力的增加几乎没有变化。主要原因为，当轴向极限抗力小时，弯头两端直管段受到的土壤轴向约束力小，从而会对弯头产生较大的推力，使得弯头内部的弯矩较大，这种情况下侧向极限抗力越大，越能够减小弯头内弯矩，从而最大Mises应力越小；而当轴向极限抗力较大时，直管段对弯头的作用较小，从而侧向土弹簧的约束起不到作用，所以最大Mises应力随侧向极限抗力几乎没有任何变化。

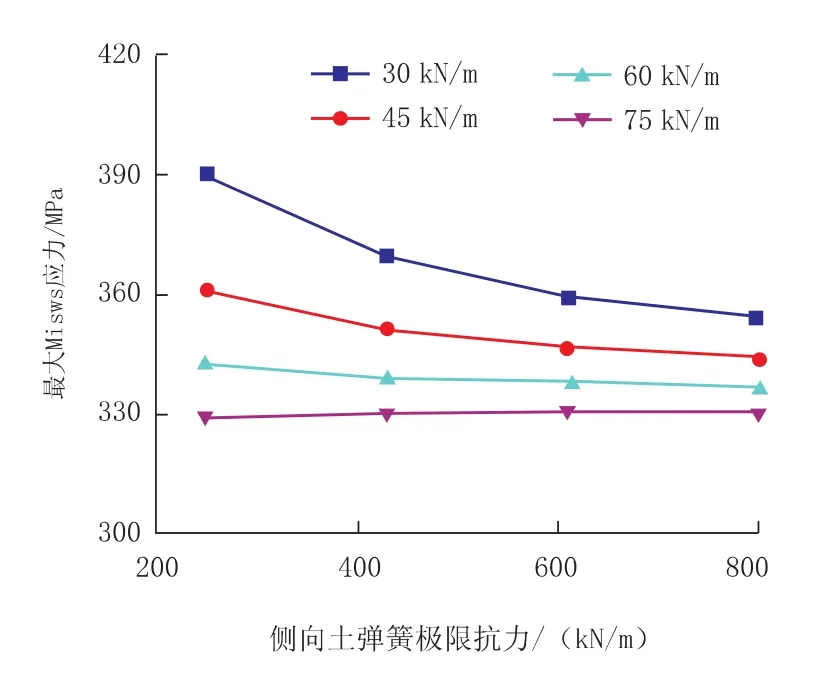
图6 管道最大Mises应力随土壤侧向与轴向极限抗力的变化规律

2.4 工作荷载的影响

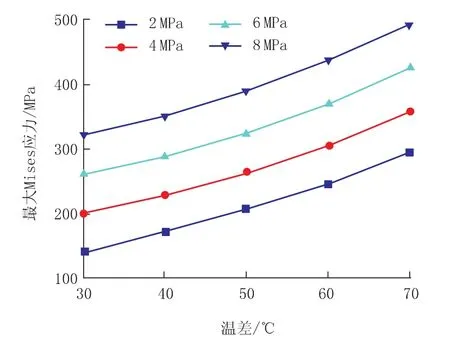
图7 管道最大Mises应力随工作温差与内压的变化曲线

弯头最大Mises应力随温差与内压的变化关系如图7所示。由图7可见，最大应力随两者的变化关系非常规律。在不同内压下，最大Mises应力随工作温差都呈现同样的幂函数关系；在不同内压下，最大Mises应力与内压基本呈线性关系。

3 结 语

针对长输管道埋地弯头结构建立了基于管土相互作用的应力计算非线性有限元模型，模型使用壳单元模拟管道，非线性弹簧单元模拟管土相互作用关系。分析了四类主要参数对弯头最大Mises应力的影响。得到结论如下：管道直径越大，弯头内最大Mises应力越大，越应受到关注。通过增大弯头的曲率半径与减小弯头夹角能够有效降低弯头内的最大Mises应力。轴向约束较小时，侧向约束越大，弯头内最大Mises应力越小；轴向约束较大时，侧向约束的影响不大。

［1］崔孝秉.埋地长输管道水平弯头的升温载荷近似分析[J].华东石油学院学报，1978（2）：54-68.

［2］梁政，袁祥忠.埋地长输管道水平弯头升温载荷下的计算问题[J].油气储运，1987，6（2）：30-36.

［3］邓道民.埋地油气管道弯头的强度计算[J].油气储运，1997， 16（11）： 3-8.

［4］陈钢，张传勇，刘应华.内压和面内弯矩作用下含局部减薄弯头塑性极限载荷的有限元分析[J].工程力学， 2005， 22（2）： 44-49.

［5］刘桢彬，王飞，王国伟，等.直埋供热管道“L”形管段的受力分析[J].太原理工大学学报，2013，44（1）：85-88.

［6］张鹏，李晓红.内压和弯矩联合作用下理想弯头的有限元分析[J].焊管， 2014， 37（2）：14-17.

［7］刘仕鳌，蒲红宇，刘书文，等.埋地管道应力分析方法[J].油气储运， 2012， 31（4）： 274-278.

［8］PENG L C.Stress analysis methods for underground pipe lines,Part 2.Soil-pipe interaction lines[J].Pipeline Industry， 1978（5）： 65-74.

［9］北京艾思弗计算机软件有限公司.CAESAR II技术参考手册[M].北京：北京艾思弗计算机软件技术有限中心，2009.

［10］博弈创作室.APDL参数化有限元分析技术及其应用实例[M].北京：中国水利水电出版社，2004：18-20.

［11］GB 50470—2008，油气输送管道线路工程抗震技术规范[S].

Complex Stress Analysis on Buried Elbow of Long Distance Pipelines

XIA Mengying1， ZHANG Hong1， LIU Xiaoben1， WU Jingtian2
（1.College of Mechanical and Transportation Engineering,China University of Petroleum,Beijing 102249,China;2.SINOPEC Tianjin Liquefied Natural Gas Co.,Ltd.,Tianjin 300457,China）

A numerical model for stress calculation of the buried elbow was built,which was established based on the nonlinear finite element method.The model adopted nonlinear soil springs to simulate the constraint effect of soil on the pipeline,using shell elements to model the pipeline.Taking the pipeline internal pressure and temperature as the load,the influence on pipeline stress of many parameters were analyzed,including pipe diameter,radius of curvature and angle,wall thickness and soil spring force,the change laws of maximal stress were obtained.The calculation results showed that the method can well simulate the stress process of the elbow,which can be used for the design and safety assessment of buried elbow.

welded pipe;buried elbow;pipe-soil interaction;non-linear soil spring;stress analysis;finite element method

TE973

B

1001－3938（2015）09-0022-04

中国石油集团工程设计有限责任公司北京分公司科学研究项目“油气田地面工程埋地管道应力分析关键技术研究”（项目号 CPEBF-2014-02）。

夏梦莹（1990—），女，硕士研究生，主要从事油气管道强度分析与安全评价研究工作。

2015-05-15

罗 刚