“数学活动经验”让思维从“感性”升华到“理性”

徐立++陈小彬

摘 要：通过数学活动，可以让学生经历数学的发生、发展过程。在以问题为载体，以学生自主参与为主的数学活动中，通过问题或任务引领学生全程参与相对完整的实践过程，展现思考过程，交流收获体会，积累活动经验，激发创造潜能，提升学生的数学素养。积累“案例”，丰富对“数学活动经验”的感性认识，激活学生已有的“生活经验”，并使之转化为“数学活动经验”，通过追问概念的内涵，提升对“数学活动经验”的理性认识。引导学生去粗取精、分类整理，或丰富己有的经验，构建正确的数学活动经验，修正原来有误的经验，或淘汰先前错误的经验，从而提升学生的数学素养。

关键词：数学活动；数学素养；数学思维

一、何为数学活动经验

《小学数学课程标准研究与实践》提出，数学活动经验是学生个体在经历数学活动的基础上获得经验，是学生经历数学活动的过程与结果的有机统一体，既包括经历数学活动所获得的经验本身，也包括经历数学活动获得经验的过程。数学活动经验既有数学知识的成分，又反映了学习者个体在某一学习阶段对相应数学对象的认识，而且是他们经历数学活动之后所留下的直接感受、体验和感悟，是知识性成分、体验性成分、观念性成分的“组合体”。

二、数学活动经验对提升学生数学素养的重要价值

1.提升学生主动发现问题的兴趣，并善于抓住数学问题中的背景和本质的素养

小学生发现问题和提出问题，进而分析和解决问题，是一个学生解决数学问题能力的综合体现。只要亲身经历发现问题、提出问题以及分析问题、解决问题的全过程，获得直接经验，通过质疑、探索、解决问题的过程，才能更深刻地理解数学的内在联系，感悟数学问题的本质。

2.提升学生的数学建模能力，培养“应用模型解决问题”的素养

让学生在一次次经历的活动中积淀、丰富。教师可以提供具体的数学活动，帮助学生获得直接性经验，引导学生进行观察、思考、比较、反思等活动，帮助学生获得替代性经验。让学生在丰富的数学活动中，对经验进行概括、内化、提升，使数学活动经验成为学生学习数学的内在支撑，构建数学模型，利用模型解决问题，从而发展学生“应用模型解决问题”的素养。

3.提升学生以“数学方式”的理性思维，从多角度探寻解决问题途径的素养

数学活动中，学生仅有一点生活经验，没有进行具体的操作，学生的经验生产是在思维层面生成的，仅在头脑里进行判断和推理，并且整个过程趋于有序。而在思维操作的过程中，生成多种方法、多种角度探索问题，提升了学生理性思维的能力，培养了学生多角度分析、解决问题的能力。

三、促进“数学活动经验”，让思维从感性体验走向理性自觉的途径

间接经验往往是直接经验的升华和内化。因此，教师引导学生积极主动地参与数学活动，经历“做”数学的过程和“思考”的过程，体验数学活动的每一个环节，以获得不同活动阶段的经验内容，促使学生的思维从感性体验走向理性自觉。

1.积累“案例”，丰富对“数学活动经验”的感性认识

（1）设计全体参与的活动。设计、组织好每一个数学活动，需要设计每个学生都能进行的、充分体现数学本质的活动，需要以学生经验为起点，积极创设基于学生数学学习需要的活动情境，激发学生的活动动机，调动他们已有的知识经验，促使他们积极主动地参与到数学活动中，并在概括和运用数学活动经验的过程中不断丰富、提升数学活动经验。

案例1：三角形的三边关系

1.探究第一个条件

师：老师这儿有4组小棒。第一组：5 cm、7 cm、10 cm；第二组：4 cm、11 cm、10 cm；第三组：4 cm、3 cm、10 cm；第四组：6 cm、4 cm、10 cm。这四根小棒是不是都能围成三角形呢？同学们动手围一围。

2.探究第2个条件

（1）质疑：蓝边10 cm，红边3 cm、黄边15 cm能围成三角形吗？

（2）操作：那么到底能不能围成三角形呢？动手围一围。

3.探究第3个条件

（1）设疑：会不会有了这两个条件还不够？还要满足其他的条件？

（2）讨论并验证：再来看三根小棒，动手摆一摆。（10 cm、3 cm、14 cm）

在教学这部分内容时，教师通过引导学生经历探究性数学活动的过程，通过行为操作、数学思维，在探索与交流中逐渐建构三角形的三边关系。在这层层递进的思维层面操作的探索活动中，学生经历了既有外显的小棒操作又有内隐的思维层面操作的探究活动，逐渐构建了三角形的三边关系。由于教师精心设计了逐步递进的问题，有效地激活了学生的数学思维，学生在经历探索三角形三边关系的过程中，不仅理解了三角形的三边关系，而且能够初步领悟探究问题的基本方法，获得较为丰富的数学活动经验。

（2）积极参与“综合实践活动”，关注各学科内部知识的联系。设计、组织好每一个数学活动，还需要特别重视引导学生积极参与“综合与实践活动”，这样的活动过程性目标重于结果性目标。例如：

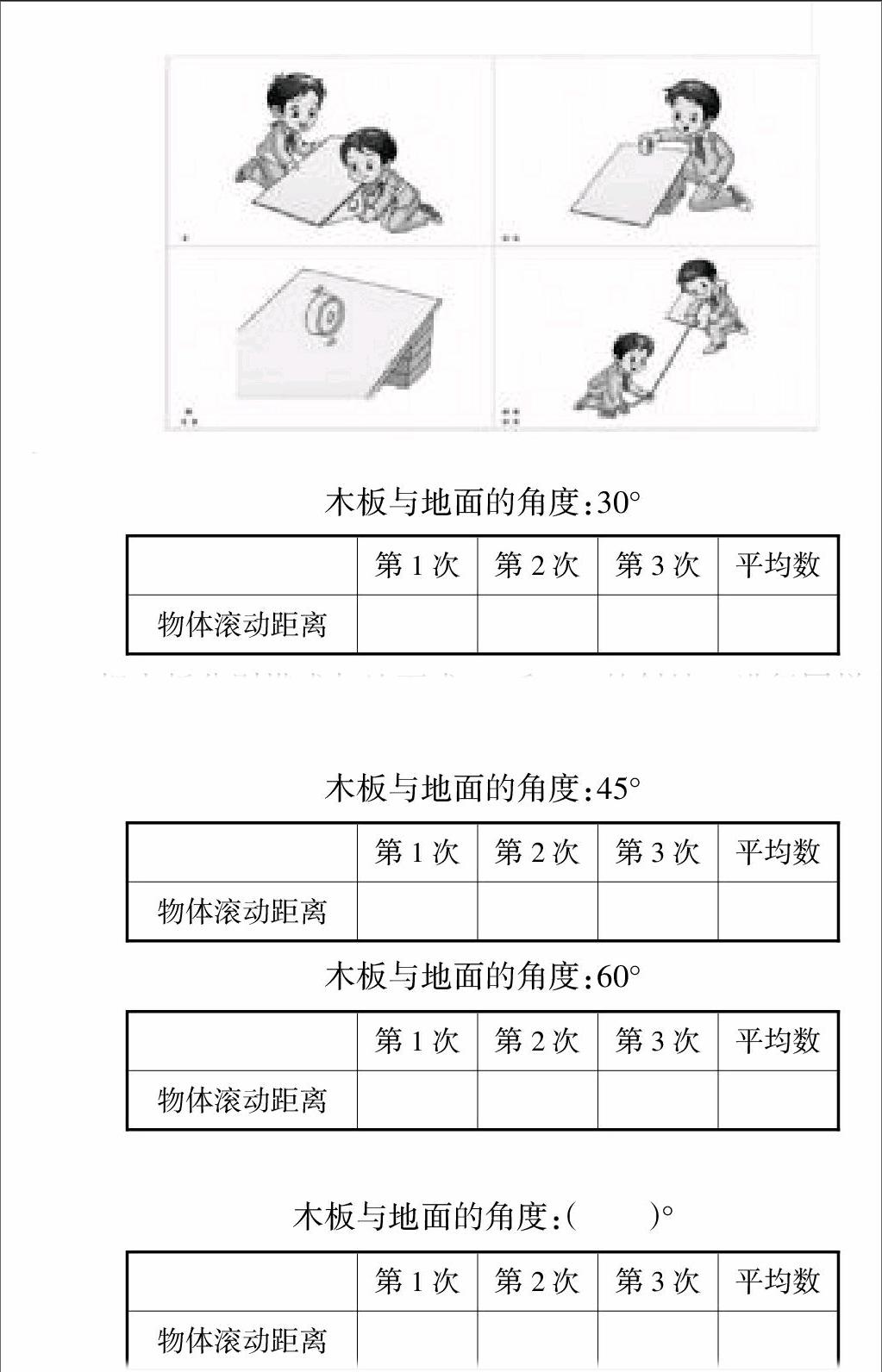
用30～50厘米长的木板在地面上搭一个斜坡，使斜坡与地面的角度为30°。再把一个圆柱形物体（如胶带圈）轻轻放在斜坡的顶上，让它自动往下滚，等物体停止滚动后，从木板的底部开始量出物体在地面上滚动的距离。

反复做几次这样的实验，记录每次量得的距离，并求出它们的平均数。

木板与地面的角度：30°

把木板分别搭成与地面成45°和60°的斜坡，进行同样的实验，并记录实验结果。

木板与地面的角度：45°

板与地面的角度：60°

各小组自己选择一个角度试一试，并记录实验结果。

木板与地面的角度：（ ）°

比较每次求得的平均数，你发现了什么？

使学生充分参与活动的全过程，注重数学与生活的联系，综合运用有关的知识与方法解决实际问题，培养问题意识、应用意识和创新意识，体验如何发现数学问题，如何选择适合自己完成的问题，如何把实际问题变成数学问题，如何设计解决方案，如何选择合作的伙伴，如何有效地呈现实践的成果并让别人体会自己成果的价值。要在以问题为载体，以学生自主参与到数学活动中，通过问题或任务引领学生全程参与相对完整的实践过程，展现思考过程，交流收获体会，积累活动经验，激发创造潜能。

2.激活学生已有的“生活经验”并使之转化为“数学活动经验”。

（1）创设生活情境。组织学生学习数学，必须考虑学生已有的知识、经验、认识发展水平、数学思维的发展水平与特点，以及学生在教师的指导下可能达到的水平。丰富的生活经验是形成数学活动经验的基础，如看钟表认时间、使用人民币买东西，测量、分辨方位、在口袋中随机摸球等生活经验，都以数学相关内容为基础。数学教学要创设源于学生生活的情境，尽量贴近学生的日常生活经验，使学生在真实的情境中学习，获得对数学活动经验的体验和数学思想方法的感悟。

（2）重视学生的认知经验。

案例2：认识周长

师：你能用自己的方式描述周长或在作业纸上表示出来吗？

师：这些都是同学们自己对周长的认识。今天我们一起来认识平面图形的周长。

师：你知道周是什么意思？你认为谁的作品正确表达了“一周”/你能指出长方形的一周吗？

师：请用提供的平面图形，把你对周长的认识和你的同桌说一说。

周长在实际生活中随处可以接触到，学生已经具有一定的认知经验，只是不完全理解这个数学术语。教师让学生对周长在熟悉的平面图上表示出来并互相交流这一认识，充分激活了学生主体已有的经验，使学生能够积极、主动地投入新知的学习，以展示学生已有的经验作为教学的开始，从平面图形一周的边线引入周长的教学，尊重学生的认识起点，既符合学生的学习实际，又有利于学生积极主动地开展后续的数学活动，进而获得新的数学活动经验。

3.追问概念的内涵，提升对“数学活动经验”的理性认识

（1）数学活动经验的积累是一个循序渐进的过程。在课堂教学过程中，教师要组织学生对参与的数学活动进行讨论与总结，引导学生检查自己的思维活动，反思自己是怎样发现、解决问题的，运用了哪些基本方法，有什么好的经验，从中回味思路，自我领悟，提升并丰富数学活动经验。当经验积累到一定程度时，要引导学生去粗取精、分类整理，或丰富已有的经验，或修正原来有误的经验，或淘汰先前错误的经验。

案例3：平行四边形面积公式

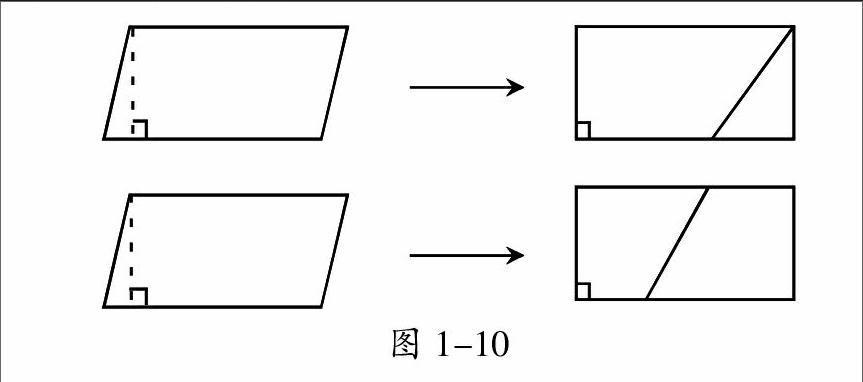
师：拿出桌上不同形状的平行四边形纸片，想一想，怎样剪一剪、拼一拼，把这个平行四边形转化成我们已经熟悉的图形？

（学生试着操作，拼出一些长方形。如图1-10）

图1-10

师：你把平行四边形转化成了什么图形？怎样转化的？

师：那我们为什么要沿着平行四边形的高剪呢？小组里先说一说。

在这个推导平行四边形面积公式的教学过程中，学生不仅能够理解面积公式，更重要的是能够进一步感悟到在学习新知识、解决新问题时，可以通过转化的策略，运用以往的知识经验去探索、解决新的问题。学生有了转化的数学活动经验，在学习三角形、梯形的面积公式时，就会自觉地运用这一经验，通过割、补、拼、移、转等方法把三角形、梯形转化成四边形，再利用平行四边形的面积公式推导出三角形、梯形的面积公式。

（2）经验的获得需要“领悟”与“转化”。通过学生动手参与活动，从而获得具体经验；然后对所经历的活动通过回顾、反思等内在的思考，内化为能够理解的合乎逻辑的、抽象的经验；最后将获得的经验在解决新问题中进行证实和运用，重新领悟和创造新的经验。经验的积累就是在这样不断循环往复的连续过程中实现经验的创造、领悟与转化。

《义务教育数学课程标准》指出：“教师应帮助学生在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。”活动经验，离不开活动，学生的数学活动经验是在参与数学活动过程的基础上获得的。没有经历数学活动，就谈不上获得数学活动经验。数学活动经验是数学活动的过程和结果，让学生在数学活动过程中，积累经验，转化经验，内化掌握数学本质，提高数学素养。

参考文献：

王林.小学数学课程标准研究与实践[M].江苏教育出版社，2011-12.

编辑 薛直艳