基于灰色GM（1,1）模型的商洛市区域环境噪声预测

刘燕，陈宁宁

(商洛学院城乡规划与建筑工程学院，陕西商洛726000)

基于灰色GM（1,1）模型的商洛市区域环境噪声预测

刘燕，陈宁宁

(商洛学院城乡规划与建筑工程学院，陕西商洛726000)

根据商洛市2010—2014年区域环境噪声的昼夜等效声级监测数据，运用灰色系统理论，建立灰色GM（1,1）模型，并用平均相对误差检验、均方差精度检验、小误差概率检验三种方法对所建模型的精度进行检验。应用检验合格模型预测得到商洛市2015年和2016年昼间一类区的噪声值分别是45.1 dB和43.24 dB，商洛市2015年和2016年夜间二类区的噪声值分别是40.83 dB和39.3 dB，并进一步得到2010—2016年商洛市区域环境噪声呈下降趋势。

商洛市；区域环境噪声；灰色GM(1,1)模型；模型检验

近年来随着商洛市城镇化进程的加快，城市区域环境噪声污染日趋严重，影响了人们的正常工作、学习和休息，已经成为商洛市日趋严重的环境问题之一。噪声污染自20世纪70年代以来被称为城市环境问题的四大公害之一,是21世纪环境污染控制的主要对象。国外对噪声的研究主要有Ana B[1]、Rajiv B[2]、Olayinka S[3]。我国对城市环境噪声污染的研究起步较晚，直到70年代，中国的声学研究所对70多个城市环境噪声进行了调查，并提出了一些相关的评价指标开启了人们对城市环境噪声的关注与研究[4]。车均[5]、崔欣[6]、任杰[7]、陆荫[8]等对不同城市噪声进行了研究，为及时有效地对城市区域噪声作出准确高效的预测，进而为治理区域环境噪声污染提供科学依据是十分必要的。本文通过建立区域环境灰色GM（1,1）模型[9],掌握未来中短期城市区域环境的发展规律和发展状况，为环境管理部门科学决策提供理论基础，为城市环境噪声污染的预防与治理提供科学依据。

1 商洛市近年区域环境噪声状况

从商洛市环境保护局[10]的环境质量公报中选取声环境质量状况中的区域环境噪声昼间和夜间的等效声级见表1和表2。其中1类区主要为居民、文教区，2类区包含居住、商业、工业混杂区，3类区主要为工业区，4类区主要为城市中的道路交通干线道路两侧区域。

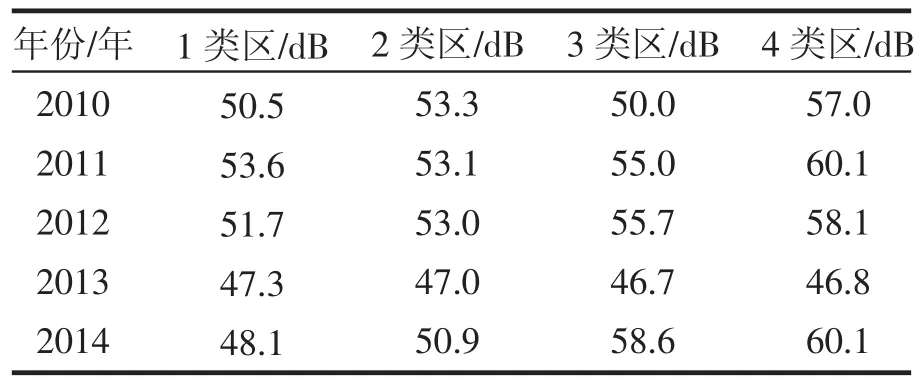
表1 2010—2014年商洛市区域功能区昼间噪声等效声级

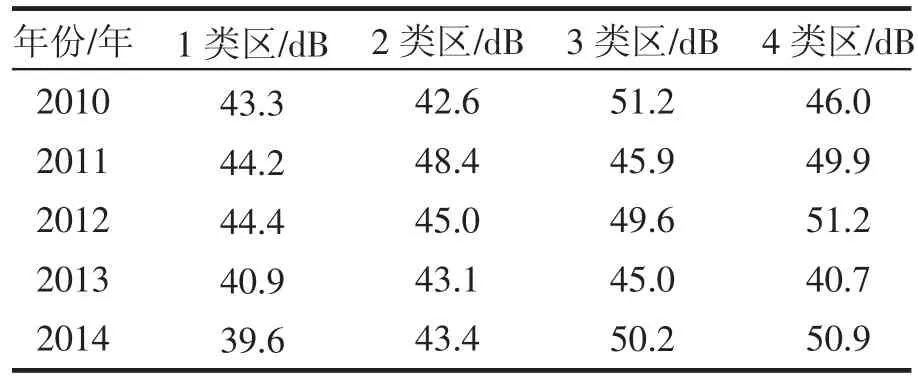
表2 2010—2014年商洛市区域功能区夜间噪声等效声级

观察表1、表2中信息，对照《城市区域环境噪声标准》（GB3096－93），可以发现昼间和夜间1类区、2类区、3类区、4类区均未超标，说明商洛市区域环境噪声的现状较为乐观。

2 灰色GM（1,1）模型

灰色理论GM（1,1）预测模型是对一组随时间变化的序列采用“累加”或者“累减”的生成方法，建立微分方程来描述系统的变化规律，使系统由“灰”变“白”，GM（1,1）为单一序列的一阶线性动态模型[11－12]。

2.1 建立模型的条件检验

1）对X(0)作准光滑性检验

设非负原始数据序列X(0)为[13]：

X(0)＝X(0)(1),X(0)(2),…，X(0)(n),X(0)(k)＞0,k＝1,…,n。

对X(0)进行一次累加生成，得到1－AGO序列X(1)为：

X(1)＝X(1)(1),X(1)(2),…，X(1)(n),

当k＞3时，p(k)＜0．5,则满足准光滑条件。

2）检验x(1)是否具有准指数规律，

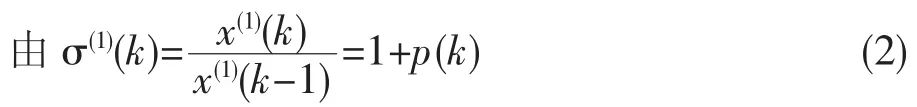
当k＞3时，σ(1)(k)∈[1,1．5]，则满足准指数条件。

只有准光滑性检验和准指数规律都满足条件才可以建立模型。

2.2 求解方程参数a和b

采用最小二乘法[14]可以求得参数a和b的值，也可以借助Matab软件进行矩阵的运算。

x(1)的紧邻生成序列：

z(1)(z(1)(2),z(1)(3),…，z(1)(n)),

对于非负准光滑序列x(0)，其1－AGO序列x(1)具有准指数规律，则x(1)白化方程（影子方程）为：

其中，－a为发展系数，b为灰色作用量。(a,b)T＝(BTB)－1BTY，

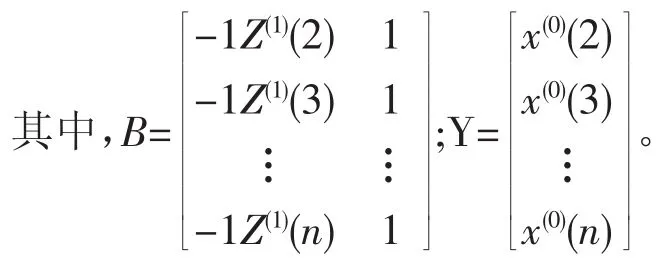
2.3 得到时间响应函数

对白化微分方程求解，可以得到时间响应函数：

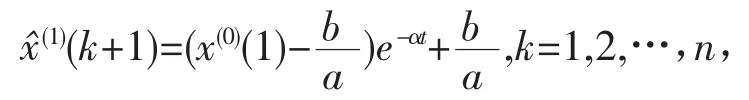
累减即可得到初始值的拟合值：

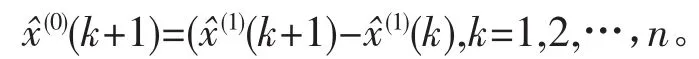
2.4 模型精度检验

模型建立之后对其进行精度检验，判断模型是否合格（见表3）。

表3 灰色精度检验等级标准

3 商洛市区域环境噪声模型的建立与检验

3.1 预测模型的建立

对2010—2014年数据检验符合标准，可以建立灰色GM(1，1)模型，故以2010—2014年商洛市昼间和夜间1类区、2类区、3类区和4类区功能区噪声等效声级监测数据作为原始数列，运用灰色GM(1，1)模型的建立过程中式(1)、式(2)和式(3)，借助Matlab软件分别计算得到预测模型：

3.2 预测模型精度检验

预测模型的精度检验有四种方法：平均相对误差检验、均方差精度检验、小误差概率检验和关联度检验。关联度检验主要是对多因素预测模型中要素之间的关联度进行分析，而本研究中只有一个变量不适合用该方法，故选用前三种方法进行精度检验。检验精度要求均方差比值越小越好、相对误差越小越好、小误差概率越大预测模型精度越高[15]。

利用式(4)－式(11)得到拟合值,对照表3进行精度检验，结果发现只有式(4)和式(9)的预测模型符合标准，故本文只出现符合标准的模型精度检验结果，见表4和表5。

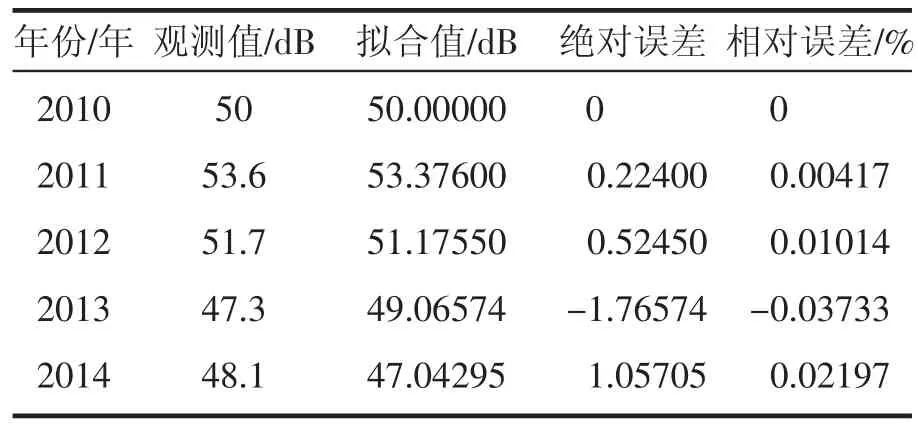
表4 2010—2014年商洛市区域环境噪声昼间1类区噪声等效声级

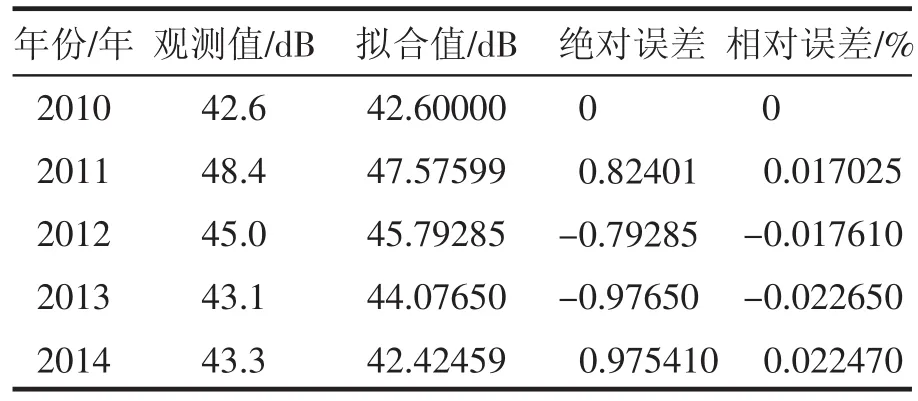
表5 2010—2014年商洛市区域功能区夜间2类区噪声等效声级（dB）

平均相对误差检验：

均方差比值检验：

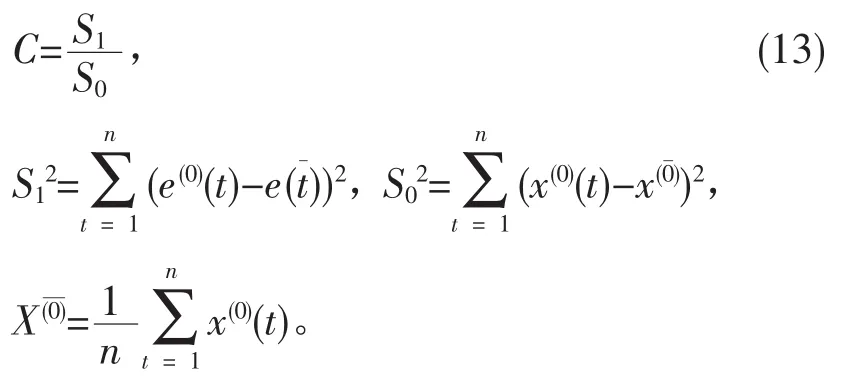
小误差概率检验：

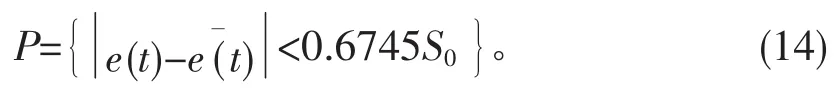
利用表4和表5的数据对照式(12)－式(14)得到灰色GM（1,1）模型精度检验结果如表6。

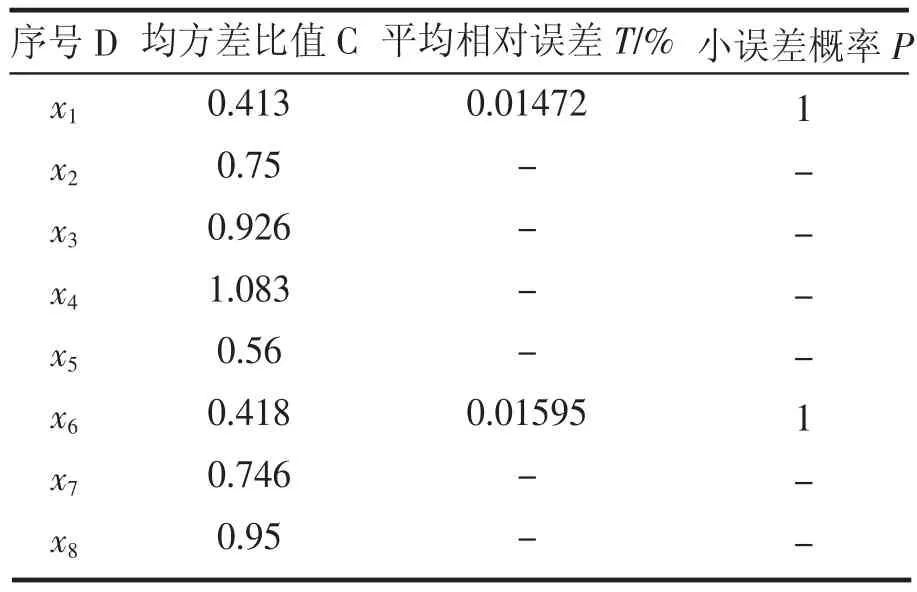
表6 灰色GM(1，1)模型精度检验结果

表6中平均相对误差T和小误差概率P“-”是因对均方差比值C大于0．5，证明其不合格，故不再对T和C值进行计算。灰色精度检验的三个标准必须同时满足，若有一项精度检验标准不满足，则证明该组数据建立的模型误差太大，该组数据建立的预测模型不能进行预测，故计算过程发现某组数据不符合其中一项标准，则不对其他两组标准进行计算。

对X1到X8八组数据建立的模型进行精度检验，发现只有第一组X1数据和第六组数据X6的精度符合精度检验标准，建立灰色GM(1,1)模型的误差较小，精度较高；其他组预测模型精度不高，预测模型不可用。第一组数据X1表示昼间1类区的噪声等效声级；第六组数据X6表示夜间2类区。故只能对昼间1类区和夜间2类区2015年和2016年区域环境噪声等效声级进行预测。

由表4和表5可以看出，所建模型对2010—2014年的城市区域环境功能区的昼间1类区等效声级拟合的绝对误差最大为1．05dB,最大相对误差为0．021197%，平均相对误差值为0．01472%。夜间2类区的噪声的拟合值绝对误差最大为0．97541 dB，最大相对误差为0．02247%，平均相对误差值为0．01595%。根据预测结果诊断表6，昼间1类区等效声级均方差C＝0．413，小误差概率P＝1；夜间2类区等效声级均方差C＝0．418，小误差概率P＝1；以上平均相对误差值均T＜1%，表明这两组模型的精度较好，用于区域环境噪声的预测可靠性相对较高。所以，第一组数据X1和第六组数据X6所得预测模型可用于预测。

3.3 商洛市未来区域环境噪声预测

采用上述建模方法，利用商洛市区2010—2014年区域环境功能区噪声的昼夜等效声级的监测数据建立灰色GM（1,1）模型，应用该模型对商洛市区未来两年的区域环境功能区（昼间1类区和夜间2类区）的噪声等效声级进行预测可得表7和表8。

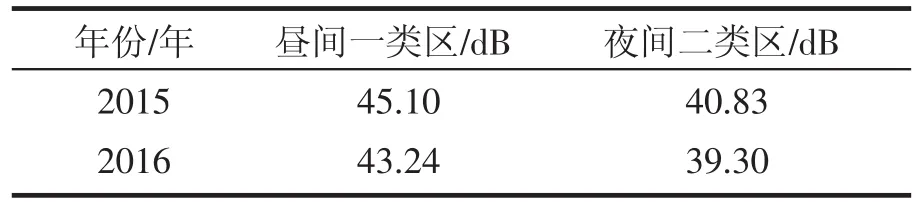
表7 商洛市未来两年昼间1类区和夜间二类区的噪声预测结果

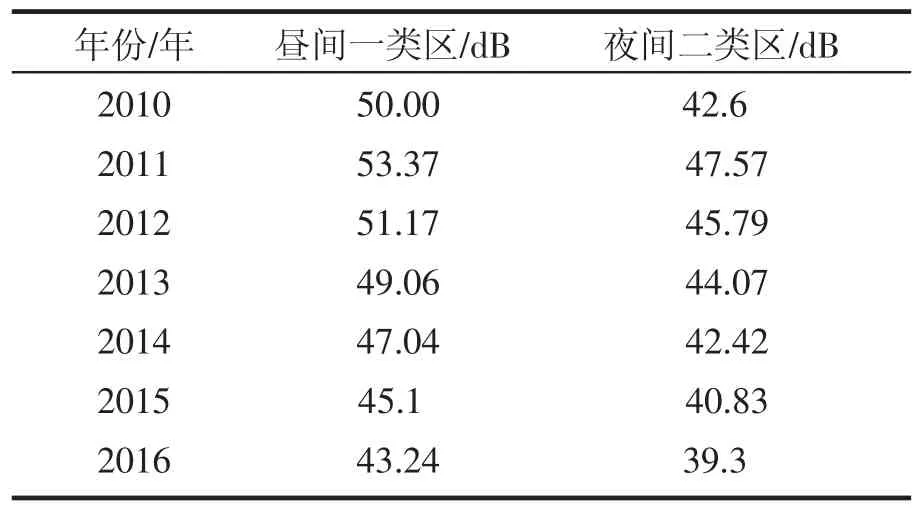
表8 商洛市2010—2016年昼间夜间噪声等效声级预测结果

由表7、表8可以看出，表7预测结果对照《城市区域环境噪声标准》（GB3096－93）可知商洛市2015年和2016年昼间1类区夜间2类区噪声等效声级预测结果均未超标。商洛市2010—2014年昼间1类区、夜间2类区噪声等效声级呈下降趋势；商洛市2010—2016年昼间1类区、夜间2类区噪声等效声级呈下降趋势，与商洛市2010—2014年昼间1类区、夜间2类区噪声等效声级呈下降趋势吻合，从侧面说明该模型可靠性。

4 结论与讨论

由预测精度检验结果可知该预测模型能较好地预测商洛市2015年和2016年昼间1类区、夜间2类区的区域环境噪声，说明运用灰色GM(1,1)模型能够适用于预测区域环境噪声的变化。所得预测结果可以为环境管理部门科学决策提供理论基础，能为城市环境噪声污染的预防与治理提供科学依据。

本研究分析可知，昼间1类区和夜间2类区噪声均呈下降趋势，商洛声环境发展趋势比较乐观。随着社会经济的发展，人们环保意识的提高，进而提高了对居民、文教区、工业混杂区的要求，促使政府及其相关部门对噪声污染的关注，进而使噪声污染的控制方面取得了显著的成果。但是这种乐观的状况只是模型对未来两年发展状况的理想模拟，很可能由于一些人为因素的干扰，导致预测结果的偏差过大。所以该预测结果可为城市环境噪声污染的预防与治理提供科学依据并引起社会高度重视。

1类区是居民、文教区，2类区是居住、商业、工业混杂区。故对噪声污染的防治主要是对居民区的治理。首先，政府要对城市功能区进行科学合理的布局，尽量使文教区、居民区远离高噪声源，对于市中心的居住区，可以建设必要的防噪隔离带；其次，各环境保护部门要找准噪声污染源，采取积极有效的措施来维护住宅区居民的正常生活秩序，建议政府部门将“优化居住质量”作为今后住宅区的政策来实施，并把住宅区及其环境的改善作为体现居民生活水平的衡量标准之一[15－16]。第三，城市噪声的污染源主要是交通噪声和施工噪声，因而对于噪声的防治要从交通噪声和施工噪声入手，对道路的路况进行改进，要及时保修毁坏路面，必要时加宽道路；加强对居住区和文教区车辆行驶和施工区域的噪声监控。

[1]Ana B,Ariza V,Francisco J,et al．Influence of urban morphology on total noise pollution:Multifractal description[J]．Science of the Total Environment,2014,532(147):270－282．[2]Hunashal Rajiv B,Patil Y.Assessment of noise pollution indices in the city of kolhapur,India[J]. Procedia-Social and Behavioral Sciences,2012,190 (37):448-457.

[3]Oyedepo O S,Saadu A A.A comparative study of noise pollution levels in some selected areas in Ilorin Metropolis,Nigeria[J].Environmental Monitoring and Assessment,2009,158(1):155-167.

[4]高延文,倪燕.噪声评价量综述[J].云南环境科学,2005,24(3):21-23.

[5]车均,高一娟.淄川区环境噪声监测与评价研究[J].环境科学与管理,2014,(39)8:134-137.

[6]崔欣.声环境功能区噪声监测技术及分析[J].环境与生活,2014,69(69):1.

[7]任杰.城市区域环境噪声在线监测系统的研究[D].北京:北京工业大学,2006.

[8]陆荫,张正煜.灰色预测GM(1,1)模型预测城市区域环境噪声[J].甘肃科技,2014,30(20):33-37.

[9]邓聚龙.灰色系统基本方法[M].2版.武汉:华中科技大学出版社,2005:20-26.

[10]商洛市环境保护局官网.2010-2014.[EB/OL].http:// hbj.shangluo.gov.c n/index/ShowClass.asp?ClassID= 15.2014.

[11]刘思峰.灰色系统理论及其应用[M].郑州:河南大学出版社,1991:12-30.

[12]樊庆锌,徐涵,石磊,等.哈尔滨市道路交通噪声分析与预测[J].哈尔滨商业大学学报:自然科学版,2011,27(6):872-875.

[13]胡坤.灰色预测评价方法与应用研究[D].南京:南京航空航天大学,2004:1-10.

[14]余鑫.灰色理论在城市道路交通噪声预测中的应用研究[D].武汉:武汉科技大学,2004:1-15.

[15]冯新宇.GM(1,1)模型在城市道路交通噪声预测中的应用[J].山西交通科技,2001,142(3):53-54,56.

[16]冯秀绒.杨凌区环境噪声监测与评价研究[D].陕西杨凌:西北农林科技大学,2007:1-20.

（责任编辑：李堆淑）

Shangluo City Regional Environmental Noise Based Gray GM(1,1)Model

LIU Yan，CHEN Ning-ning
（College of Urban,Rural Planning and Architectural Engineering,Shangluo University,Shangluo 726000,Shaanxi）

According to equivalent sound level monitoring data of regional environmental noise during 2010-2014 in Shangluo,by gray system theory,gray GM(1,1)model is set up,and three methods to test the accuracy of the model is used,namely the average relative error test,the average variance accuracy test and small error probability test.It is predicted that regional environmental noise by this model in 2015 and 2016 in Shangluo is 45.1dB and 43.24 dB during the day in Area I,and 40.83 dB and 39.3 dB during the night in Area II.It shows that the trend of regional environmental noise,during 2010-2016 in Shangluo is decreasing.

Shangluo City;regional environmental noise;Grey GM(1,1)model;model test

X593

A

1674-0033（2015）06-0071-04

10.13440/j.slxy.1674-0033.2015.06.017

2015-10-21

陕西省教育厅专项科研计划项目（14JK1214）

刘燕，女，陕西洛南人，硕士，讲师