永磁同步电机的自调整灰色预测内模控制

孟芳芳，邵雪卷

(太原科技大学 电子信息与工程学院，山西 太原 030024)

0 引言

永磁同步电机(PMSM)调速系统具有时变、非线性、强耦合等特征，传统PID控制计算简单，能满足一般控制系统性能要求，但PID控制器参数优化困难、抗干扰能力弱、对负载的适应能力差，一些新型控制策略表现出更好的应用前景［1］。灰色预测控制能利用系统数据的发展变化规律对未来行为进行预测，通过对系统提前控制来提高系统的适应能力［2］。近年来，灰色预测在电机控制中已经得到广泛研究，文献［3］将灰色系统预测理论应用到电机转子位置和速度预测上，通过灰色关联度分析确定转子位置及速度的有效预测因子。文献［4］将灰色预测用于电机可靠性分析，并根据已有电机的可靠性数据对所给模型进行仿真。许多专家学者试图将灰色预测与其他先进控制相结合应用于复杂快速随动系统［5］。文献［6］提出一种新型自调节控制器，可依据预测精度在线调节控制器，提高了系统鲁棒性。内模控制仅有一个参数，计算简单，调整方向明确，控制器具有PI结构［7］。本文针对永磁同步电机调速系统提出自调整灰色预测内模控制设计方法，利用自调整灰色预测在线实时对转速误差进行预测，并可依据预测模型精度在线自动调整预测误差和当前误差所占比例，以提高系统的抗扰动性和鲁棒性，内模控制依据系统下一时刻的输出响应误差控制输出变量。最后在MATLA/Simulink的仿真环境下对矢量控制PMSM调速系统运用此方法进行仿真研究，表明了此方法的有效性。

1 PMSM数学模型

永磁同步电机(Permanent Magnet Synchronous Motor，简称PMSM)调速系统通常采用基于id=0矢量控制，通过坐标变换，永磁同步电机具有像直流电机同样的表达形式。

PMSM的运动方程为:

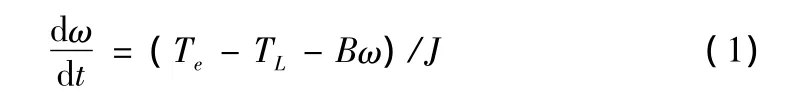
其中ω是电机机械角速度;Te、TL分别是电磁转矩、负载转矩;B是粘滞摩擦系数;J是转动惯量。

电磁转矩方程为:

其中Pn是电机极对数;ψf是转子磁链;iq是定子交轴电流分量。

令TL=0，对式(1)进行拉氏变换，则 PMSM模型传递函数为:

2 自调整灰色预测内模控制

2.1 内模控制器设计

内模控制器仅有一个参数可调节，算法简单，鲁棒性强，能消除对未知干扰的影响，当转速环采用内模控制设计时，其原理框图如图1。

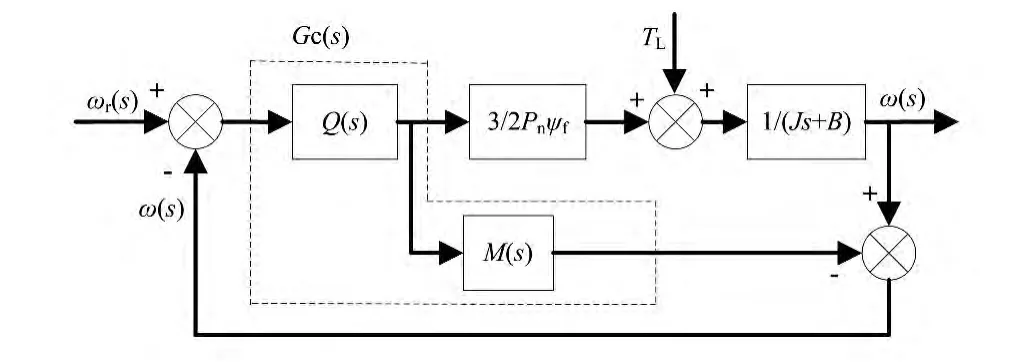
图1 内模控制PMSM速度控制系统结构图

由图1可得:

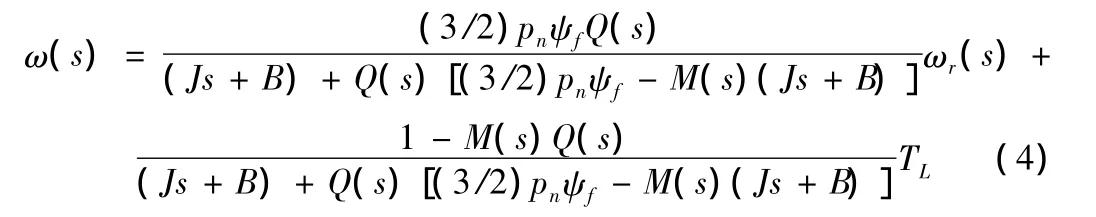
由式(4)可知，当数学模型和被控对象匹配时，即:M(s)=(3/2Pnψf)/(Js+B)时，依照内模控制器设计原理，在设计控制器Q(s)需增加一个低通滤波器L(s)，以确保系统的稳定性，增强模型失配时的鲁棒性。L(s)的表达形式如下:

其中λ是滤波器的时间常数，则内模控制器为:

等效控制器GC(s)为:

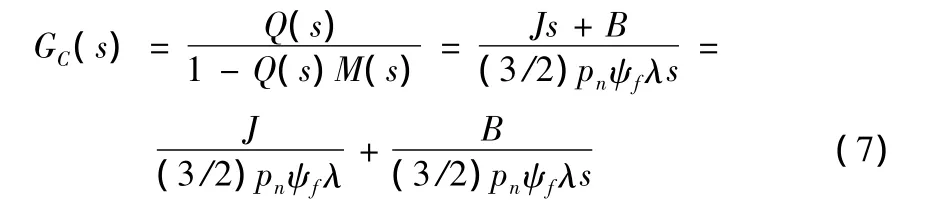
由式(10)可知，内模控制器具有PI控制结构，有且仅有一个参数λ可调，计算公式简单，调整方向明确，对未知干扰鲁棒性较强。λ值与控制系统的动态特性有关，λ取值越小，输出响应越快，但超调量较大;λ取值越大，输出响应越慢，但超调量较小。

2.2 灰色预测控制

GM(1，1)模型是在灰色预测中最常用的模型［8］，它通过对原有数据使用累加生成的数据处理方法，得到一条呈现指数增长趋势的上升数列值，建立一阶微分方程模型，再经累减生成操作即可得到预测数列。灰色预测控制具有实时控制性好，噪音不用过滤，结构简单易懂，单变量多变量兼容，对环境适应性好等优点。

设已知系统原始序列为:

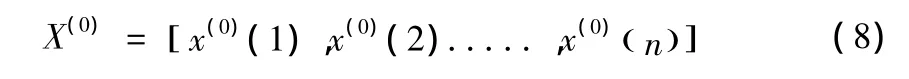
对上式序列累加一次，可以得到序列:

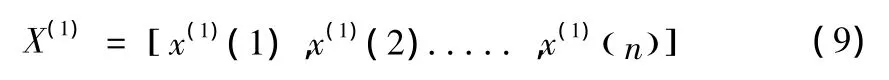
其中:

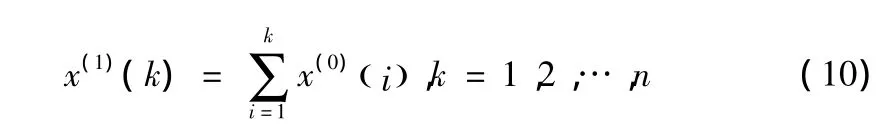
对序列X(1)进行相邻均值的生成，得到生成序列Z(1)如下:

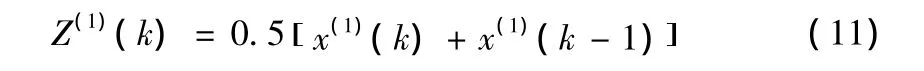
其中 k=1，2，…，n

可得 GM(1，1)的灰色微分方程［9］:

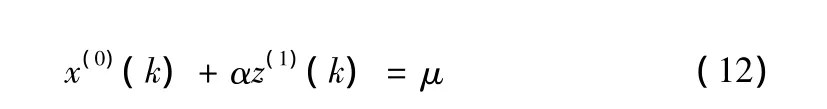
则相应的白化方程为:

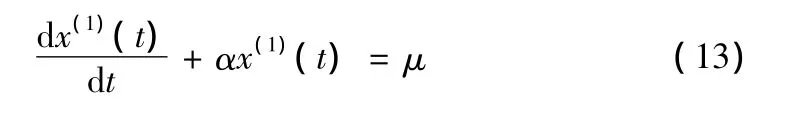
其中α称为发展系数、μ为灰色作用量，两者可以用最小二乘法求得:

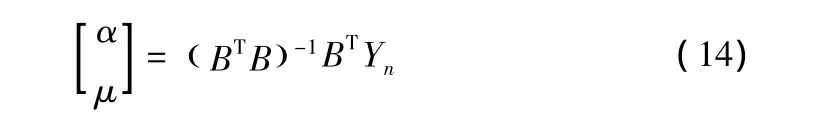
其中:

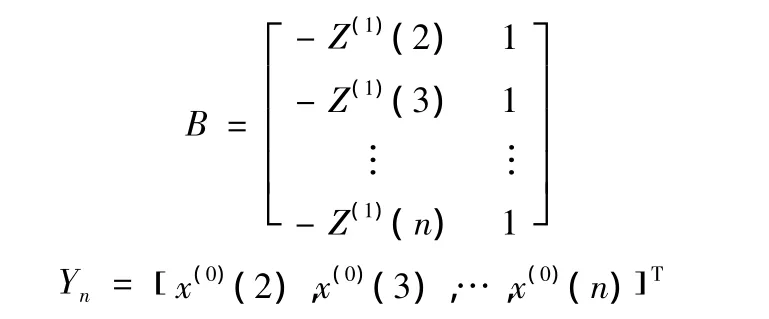
则方程(13)的解为:

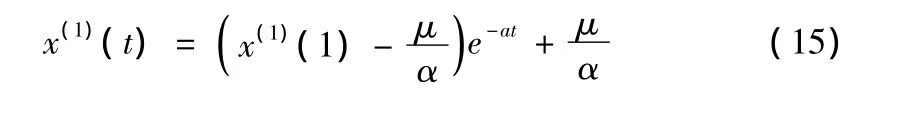
相对应式(15)的时间响应序列为:

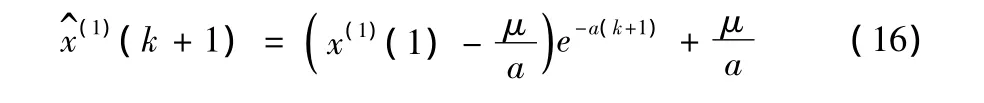
其中 k=1，2，…，n

通过对上序列x^(1)进行累减生成操作可得预测序列x^(0)。

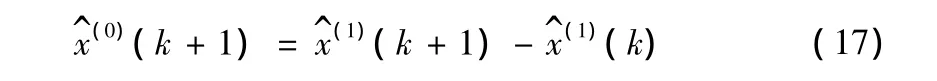
其中 k=1，2，…，n

2.3 基于新陈代谢式自调整灰色预测内模控制

传统的控制器是根据当前误差计算下一时刻的控制变化量，灰色预测控制能根据当前系统误差来预测未来系统误差。自调整灰色预测则将当前误差和预测误差进行有效综合，并根据预测模型精度来实时调整不同误差所占比例，来提高控制系统的精确性。当模型精确度高时，灰色预测在控制系统中的作用量权值增强，当模型精确度低时，灰色预测在控制系统中的作用量权值减弱。其控制原理框图如图2所示。

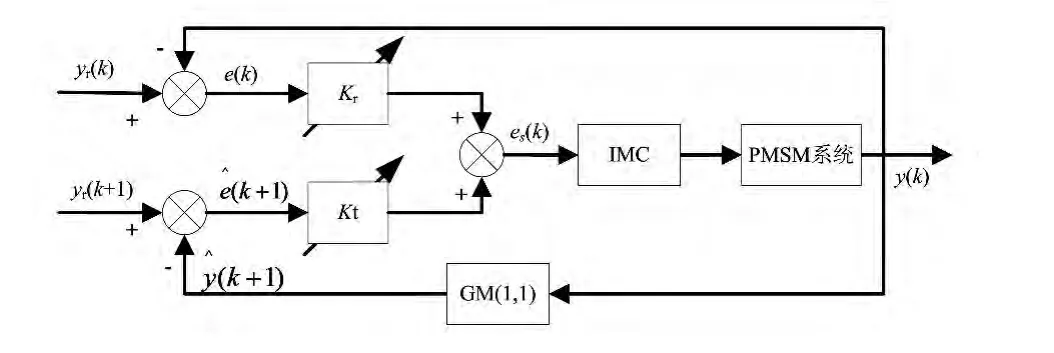
图2 自调整灰色预测内模控制原理框图

图(2)中yr(k)、yr(k+1)分别为k、k+1时刻的系统速度参考值，e(k)、(k+1)分别为k时刻实际误差，k+1时刻预测误差，Kr、Kt分别为当前误差和预测误差所占的权值，es(k)为合成误差。从图中可知:

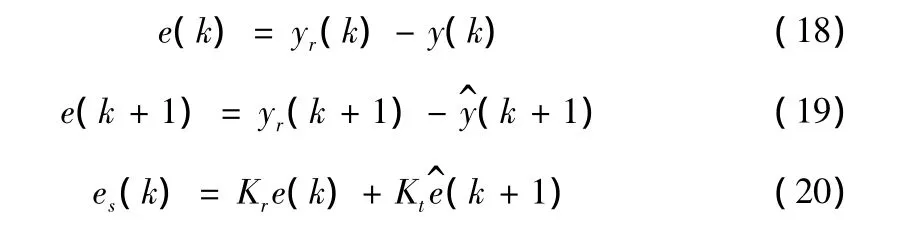
通过调整Kr、Kt的值，可以改变当前误差和预测误差在合成误差中所占的比重，两者取值范围都为［0，1］。灰色预测的模型精度决定Kr、Kt的值，若预测精度变高，Kt取值变大，Kr取值变小，反之，预测精度变低，Kt取值变小，Kr取值变大，这样可以避免预测误差对系统的不良影响。本文选用残差检验中的平均相对误差对模型精度进行检验，计算公式如下:

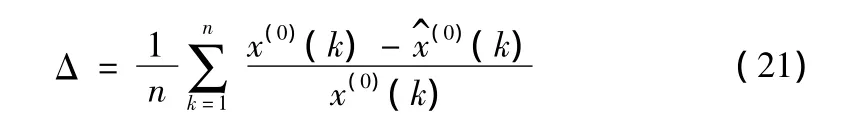
平均相对误差作为模型的精度的检验指标，它取值越小，表明模型精度相对越高。这里取模型的平均精度为:

为避免合成误差增大，本文取:

图(2)中GM对下一刻实时转速通常用新陈代谢模式来进行预测，即前一个旧数据的去除都是后一个新数据输入为前提，每时有一个新模型形成，随之得到一组新的预测值，用于建模的数据列维数是一恒值，但预测系统的变量是随时间而发生变化的，因此系统适应能力很强。

3 仿真研究

基于MATLAB/Simulink仿真环境下搭建的PMSM控制系统仿真模型如图3所示。电流控制器为传统的PI控制，速度控制器采用本文设计的自调整灰色预测内模控制。永磁同步电机选用MATLAB/Simulink自带的模型，参数为:额定转矩为 0.8 N·m，额定转速为3 000 r/min，漏磁通 ψf=0.171 7 ωb，转动惯量J=2.26 ×10-5kg·m2，极对数 Pn=2，粘滞摩擦系数 B=1.349 ×10-5N·m/(rad·s)。

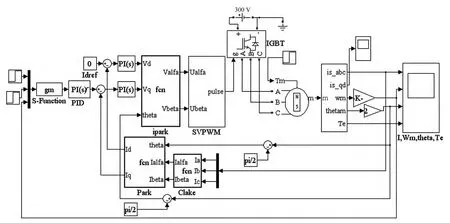
图3 系统仿真Simulink模型图

根据内模控制原理，综合考虑系统的快速性和鲁棒性，内模控制器中参数λ选为0.001。在灰色预测中，通常系统的惯性越小，预测步数越小，电机调速为快速控制，实时性较强，本文建模维数选为k=5，预测步数选为1。为验证本方法的有效性，永磁同步电机速度调节器分别采用文献［6］自调整灰色预测控制、内模PI控制及本文所设计方法跟踪恒值转速响应曲线如图4所示，在0.04 s时，加入幅值为0.5 N·m的干扰信号，不同控制器的转速响应曲线仿真结果如图5所示。

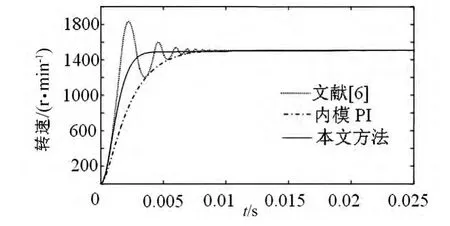
图4 采用不同控制器时输出转速波形

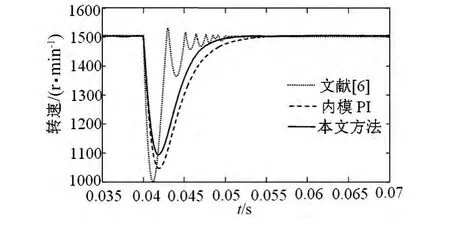
图5 受到扰动时采用不同控制器速度波形

由图4可知，自调整灰色预测内模控制输出转速响应平稳，没有超调，无震荡，大大缩小了响应时间，其动态性能明显优于单一内模控制和自调整灰色预测。由图5可知，在0.04 s时，加入幅值为0.5 N·m的干扰信号，本方法转速降落400每分转为最少，这是由于自调整灰色预测为“超前控制”，能预测系统将来输出变化而提前改变控制量的输出，迅速返回到稳态值。仿真结果表明该设计方法跟随性能好且具有较强抑制干扰能力和良好的鲁棒性。

4 结束语

本文将自调整灰色预测和内模控制各自优点综合使用，内模控制先计算出控制器参数，保证系统快速性，自调整灰色预测能在线依据GM预测精度在线自动调整预测数据在系统中所占的比例，提高了控制系统的适应能力。仿真结果表明，该方法较传统单一控制器能明显提高响应速度能力和抗干扰能力，适用于

PMSM实时控制调速系统。

［1］王雷，蒋静坪.无刷直流电机自适应补偿最优状态反馈速度控制［J］.中国电机工程学报，2008，28(24):101-107.

［2］TRUONG D Q，AHN K K.Force Control for Hydraulic Load Simulator Using Self-Tuning Grey Predictor-Fuzzy PID［J］.Mechatronics，2009，19(2):233-246.

［3］祝晓辉，李颖晖，陈玉峰.永磁同步电机转子位置及速度提取灰色预测法［J］.电机与控制学报，2009，13(2):184-189.

［4］朱显辉，崔淑梅，师楠，等.电动汽车电机可靠性的灰色预测模型［J］.电机与控制学报，2012，16(8):42-46.

［5］RUEY JING LIAN.Grey-prediction self-organizing fuzzy controller for robotic motion control［J］.Information Sciences，2012，202(12):73–89.

［6］张广立，付莹，杨汝清.一种新型自调节灰色预测控制器［J］.控制与决策，2004，19(2):212-215.

［7］吴晓威，张井岗，赵志诚.基于灰色预测的自适应内模PID双重控制器设计［J］.智能系统学报，2008，3(1):71-76.

［8］GUO HUAN，XIAO XIN-PING，FORREST JEFFREY.A research on a comprehensive adaptive grey prediction modelCAGM(1，N)［J］.Applied Mathematics and Computation，2013，225:216-227.

［9］周国雄，吴敏.基于改进的灰色预测的模糊神经网络控制［J］.系统仿真学报，2010，22(10):2333-2336.