基于SVPWM的异步电机矢量控制及调节器设计实现

杨圣蓉，王剑平，张果

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

0 引言

异步电动机矢量控制技术是由德国学者K.Hass和F.Blaschke在20世纪70年代初建立起来的［1］。矢量控制(Vector Control)又称磁场定向控制(Field Oriented Control)，就是将交流电机空间磁场矢量的方向作为坐标轴的基准方向，其实际是一种解耦合控制，通过坐标变换和其它一系列的数学运算，将交流电机的定子电流分解为按磁链定向的励磁电流分量isd和转矩电流分量isq，再通过仿照直流电动机的控制方法对这两个电流分量单独控制实现对电磁转矩和磁通的分离控制［2-3］。

空间电压矢量PWM(Pluse Width Modulation)逆变器以控制磁通正弦为目标的磁链跟踪控制技术，以不同的开关方式在电机中产生的实际磁通去逼近定子磁链的给定轨迹——理想磁通圆，来确定逆变器的开关状态，形成PWM波形。由于其控制简单、数字化实现方便，且直流母线电压利用率高，已呈现出取代传统SPWM(Sinusoidal Pulse Wide Modulation)的趋势［4］。

关于矢量控制的资料有很多［5-8］，但是多着眼于工作原理以及直接应用，具体涉及到矢量控制中调节器设计方法及参数整定的却很少。文献［5］提出了一种新的基于扩展卡尔曼滤波器的观测器来估计电机的磁链和转速，在文献搭建的系统框图中，与传统矢量控制一样用到了两个电流调节器ACRd、ACRq和一个转速调节器ASR，但文献中未提及这3个调节器具体的设计及实现原理。文献［6］基于变结构控制和自适应控制理论，提出一种新颖的变结构模型参考自适应观测器，用于矢量控制系统的转速辨识，在系统原理图中也涉及到调节器。可见，无论在传统矢量控制的基础上提出何种新的技术或方法来改善系统性能，不管是只使用计算机进行仿真测试还是在实际中采用软件编程实现，只要在矢量控制中使用PI调节器，对调节器的设计都是一个必不可少的环节。本文采用理论分析与MATLAB建模与仿真实验的方法，在前人的基础上，通过Simulink环境基于SVPWM技术完成感应电机矢量控制的设计仿真，并提出具体的实现矢量控制中调节器参数整定的方法，为下一步实际的设计提供了理论依据及必要的系统参数。

1 异步电动机按转子磁链定向的数学模型

由异步电机的物理模型和数学模型可得出按转子磁链定向的数学模型如下:

其中 np为交流电动机的极对数，Lm、Lr、Ls为绕组互感，转子自感和定子自感;ist、ism为定子电流转矩分量和励磁分量;ψr、σ为转子磁链和漏感系数。

2 矢量控制和SVPWM的原理及实现

2.1 矢量控制的原理及实现

矢量控制的原理结构图如图1所示。

图1 矢量控制系统原理结构图

由图1可以看出，从给定输入到等效直流电机的输出，异步电机的直流等效过程就是解除异步电机非线性耦合关系简化其数学模型的过程。在这个过程中，涉及三种坐标系统:三相静止坐标系(3s)、两相静止坐标系(2s)和两相旋转坐标系(2r)，三相异步电机模拟成直流电动机进行控制需将三相变换到两相，以及静止坐标系变换到旋转坐标系。

从三相到两相的变换关系为:

逆变换关系为:

两相静止和旋转坐标系中的磁动势矢量如图2所示。

两相静止坐标系和旋转正交坐标系中的磁动势矢量

由图 2 可见，iα、iβ和 id、iq之间存在下列关系:

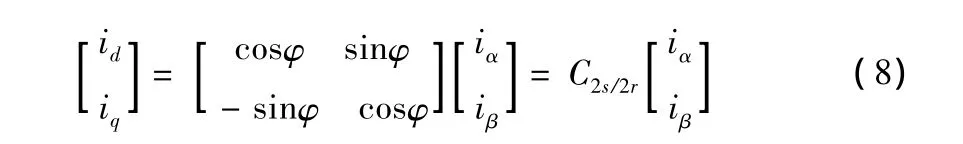
旋转正交坐标系到静止两相正交坐标系的变换为:

2.2SVPWM的原理及实现

交流电动机需要输入三相正弦电流的最终目的是在电动机空间形成圆形旋转磁场，从而产生恒定的电磁转矩。把逆变器和交流电动机视为一体，以圆形旋转磁场为目的来控制逆变器的工作，这种控制方法称为“磁链跟踪控制”。磁链轨迹的控制是通过交替使用不同的电压空间矢量来实现的，所以又称为“电压空间矢量(Space Vector PWM，简称SVPWM)控制”。

SVPWM是从三相输出电压的整体效果出发，着眼于如何使电机获得理想圆形磁链轨迹。SVPWM技术与SPWM相比较，绕组电流波形的谐波成分小，使得电机转矩脉动降低，旋转磁场更逼近圆形，而且使直流母线电压的利用率有了很大提高，且更易于实现数字化。

SVPWM的实现分为如下几步:判断矢量所在扇区N;计算开关矢量的作用时间;确定开关管导通时刻;生成6路PWM波形。其实现过程如图3所示。

图3 SVPWM的实现

3 系统解耦及调节器设计

异步电机矢量控制系统已得到广泛应用，介绍它的资料很多，但大多着眼于工作原理及对电机参数的辨识，在很多文献中仅仅搭建出仿真模型得出仿真结果，没有提及调节器设计的方法以及参数整定的过程。

依据矢量控制的基本原理得到基于SVPWM的矢量控制仿真模型，选择的电机为给定的15 kW标准电机，母线电压VDC给定530 V，负载TL给定为空载启动，在0.3 s时加负载40 N·m。以下根据所选定的电机进行电流调节器和转速调节器的参数整定。

3.1 电流调节器设计

由图1可知电流控制模块中，有两个直流电流调节器ACR1和ACR2，两个调节器均选用传统的PI调节器。它们的输入分别是定子电流dq轴分量的给定值id*、iq*和实际反馈值id、iq。电流调节器模块的设计思想是:通过电流调节器ACR1得到定子电压q轴分量Vqref来控制定子电流q轴分量iq;同理，通过电流调节器ACR2得到定子电压d轴分量Vdref来控制定子电流d轴分量id。若电机的d轴电流分量只受d轴电压控制，q轴电流分量只受q轴电压控制，则系统是解耦的。解耦过程如下:异步电机的定子电压矢量为:

其中定子磁链矢量ψs以及转子磁链矢量ψr分别可表示为:

其中Lsσ和Lrσ为定子和转子漏感。

由(11)(12)以及在忽略 LsσLrσ/Lm

2二阶小量以后得:

其中Lσ为定转子全漏感，σr为转子漏感系数，σr=Lrσ/Lm。

由于电机已选定，则电机互感Lm和定转子全漏感Lσ为已知量，但是转子漏感Lrσ很难从Lσ中分离出来。通常Lrσ＜＜Lm，式(13)可化为:

因此有:

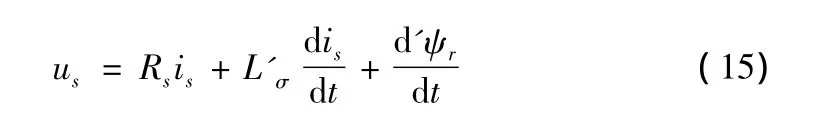
可认为在电流调节期间，ψ'r保持不变，即于是可得到:

又由 us=(usd+jusq)ejφs，is=(isd+jisq)ejφs，

带入式(15)得:

由式(16)可知dq轴的电压电流之间存在耦合，它们还与ωs和ψr'之间存在耦合，导致电流调节器设计困难，不能直接使用单变量线性系统工程设计方法。通过引入定子电流预控环节［9］等一系列的处理，最终可将式(16)变换为:

由式(17)可知，对调节器而言，控制对象是无耦合的一阶惯性环节，因此可以用常规的工程整定方法来设计调节器的参数。由以上矢量控制系统的解耦推导过程可得，电流环的近似动态结构框图如图4所示。

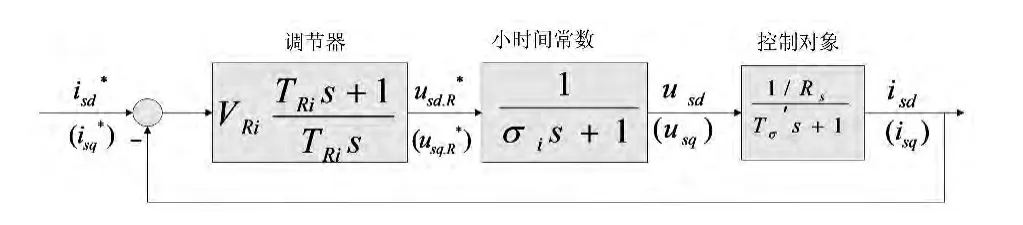
图4 电流环动态结构框图

图4 中VRi和TRi是调节器的比例系数和积分时间常数，σi是电流中小时间常数之和，包括PWM滞后及滤波等。根据西门子公司提出且在国际上仍通用的“调节器最佳整定法”［7］，调节器应选用PI调节器，且:

因此，要得到电流环PI调节器的参数，只需要知道σi。根据工程经验，要计算小时间常数，只需要将电机开环并供电，在空载情况下直接测量电流稳定所需时间，其达到最大值所需时间的0.632倍即为小时间常数σ。测量模型如图5所示。

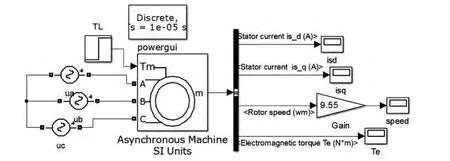
图5 估算小时间常数模型

运行图5所示的模型，得到电流在0.007 7 s时达到最大，可得

因此理论上电流环的 PI参数为:P=0.43，I=0.43/0.019 5=22。

3.2 转速调节器设计

同电流调节器的解耦过程相类似，这里不再赘述，直接得到转速环的动态结构框图如图6所示。

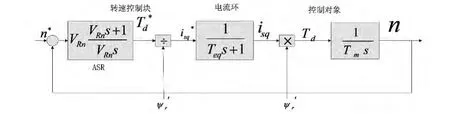
图6 转速环动态结构框图

与电流调节器的设计思路一样，为了得到转速调节器的PI参数，只需要知道小时间常数Teq和机电时间常数Tm。本文所使用的电机额定转速为1 460 r/min，由此可知当转速达到0.632×1 460=923 r/min时所需要的时间就是Tm。由图5运行所得数据可以估算 Teq=0.057 7 s，Tm=0.022 8 s。

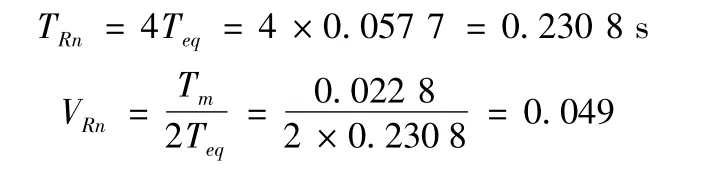
因此理论上转速环的 PI参数为:P=0.049，I=0.049/0.230 8=0.21。

4 系统测试

系统运行结果如图7(a)、(b)、(c)所示。

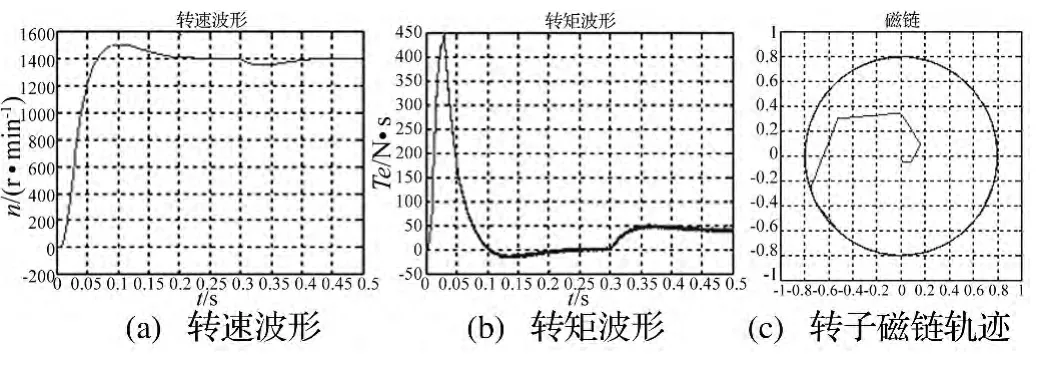
图7 仿真结果

由图7(a)所示的转速波形可以看到，在矢量控制作用下，转速很快达到给定，且转速超调很小，符合设计要求。加负载以后有少许下降但随即恢复，最终稳定在给定值。符合转速跟随给定的特性。跟随给定和超调量小也说明设计的调节器参数较合理，从而验证调节器设计和参数的整定方法是有效的。

由转矩特性曲线可以看到，空载启动过程中转矩迅速增加然后下降为0，最终电磁转矩与负载转矩相等，这是电机稳定的必要条件。加入负载以后，电磁转矩从零迅速增加到负载转矩值，并最终保持恒定。

从磁链轨迹可以看出系统整个控制效果很理想，达到了SVPWM的最终目的:控制转子磁链，使之最终成为圆形。

由上述测试结果可知，通过工程整定后得到的转速环和电流环的参数能满足系统性能指标:响应快速，超调较小，能跟随给定。

5 结束语

本文在转子磁链定向电动机数学模型的基础上，利用MATLAB/Simulink进行了基于SVPWM的矢量控制调速系统仿真设计，通过测试结果可知系统总是能跟随给定转速的变化，实现无偏差控制;矢量控制系统具有控制精度高，调速范围宽，动态响应快等优良性能。同时推导了矢量控制系统的解耦过程，所介绍的调速系统调节器参数整定准则和方法，对于快捷、准确地选择合适的闭环参数，有很大的实践应用价值。

［1］WATANABE E，ISHII S，YAMAMOTO E，et al.High performance motor drive using matrix converter［C］.Advances in Induction Motor Control(Ref.No.2000/072)，IEE Seminar.IET，2000:7/1-7/6.

［2］石严.刍议异步电动机转子磁场定向矢量控制系统［J］.Science＆Technology Information，2009，3(1):525.

［3］曹先庆，朱建光，唐任远.基于模糊神经网络的永磁同步电动机矢量控制系统［J］.中国电机工程学报，2006，26(1):137-141.

［4］ZHAI L，LI Z.Modeling and simulating of SVPWM control system of induction motor in electric vehicle［C］.Automation and Logistics，2008.ICAL 2008.IEEE International Conference on.IEEE，2008:2026-2030.

［5］李旭春，张鹏，赵非.改进EKF的异步电机无速度传感器矢量控制［J］.电机与控制学报，2013，9(17):24-29.

［6］王庆龙，张崇巍，张兴.交流电机无速度传感器矢量控制系统变结构模型参考自适应转速辨识［J］.中国电机工程学报，2007，15(27):70-74.

［7］刘洋，王庆义，赵金.基于矢量控制系统的双随机PWM技术研究［J］.中国电机工程学报，2010，36(30):24-29.

［8］邓青宇，廖晓钟，冬雷，等.一种基于定子磁场定向矢量控制的异步电机磁链观测模型［J］.电工技术学报，2007，22(6):30-34.

［9］马小亮.矢量控制系统的解耦与调节器设计［J］.电气传动，2009，39(1):3-6.