基于SystemView的4位m序列发生器数学模型的分析及电路设计
陈军
(定西师范高等专科学校 物理与电子工程学系,甘肃 定西 743000)
0 引言
在现代工程实践中,伪随机码(PN)在导弹、卫星、飞船轨道测量和跟踪、雷达、导航、移动通信、保密通信和通信系统性能的测量以及数字信息处理系统中得到广泛应用[1-3]。如,在连续波雷达中可用作测距信号,在遥控系统中可用作遥控信号,在多址通信中可用作地址信号,在数字通信中可用作群同步信号,还可用作保密通信中的加密作用等。伪随机序列具有预先的可确定性和可重复性,且表现出白噪声采样序列的统计特性,利用其性质加密数字信号使加密后的信号在携带原始信息的同时具有伪噪声的特点,它对不知其生成方法的探测者而言,如同真的随机序列一样不可预测,以达到在信号传输的过程中隐藏性目的。在信号接收端,再次利用伪随机序列加以解密,提取原始信号。最长线性移位寄存器序列(简称m序列)作为一种基本的PN序列,是带线性反馈移位寄存器的周期最长的一种基本序列。它具有较强的系统性、规律性和相关性[4-6]。
本文首先详细地分析了m序列的数学模型结构,然后运用SystemView软件对4位m序列生成器电路进行了设计研究,最后分析仿真、测试结果。
1 m序列发生器的数学逻辑模型
m序列是由一个线性反馈的n级移位寄存器生成的[7-9]。其实质是反馈函数中仅包含模2加运算的线性运算。在具有线性反馈的移位寄存器生成的序列中,最后一级线性反馈移位寄存器输出的序列满足的逻辑函数,

即为m序列,其中参量ci被称为反馈系数,其取值决定了移位寄存器的反馈的连接线状态,它也决定了生成m序列的结构状态;Di表示第i级寄存器的状态,它们的值均取0或1。当反馈系数ci为1时,表示参与反馈,反之,则表示断开反馈线,即无反馈连线。(1)式的特征多项式为:
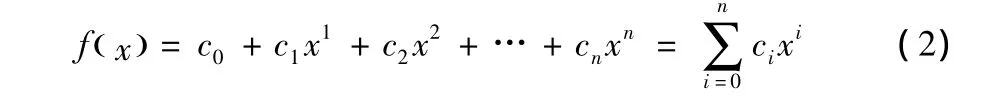
m序列个数计算公式:
n级移位寄存器共有2n种状态,除去全0状态外有2n-1种状态,因此它能产生的最大长度的码序列为2n-1位。这样生成的m序列是一个以P=2n-1为周期的循环序列。
以4级移位寄存器产生m序列为例进行分析如下:
由公式(3)可计算4级移位寄存器可以产生2个m序列[10-13],其一的反馈系数 Ci=(23)8=(10011)2,其中 C0,C1,C2,C3和C4均为反馈线,可见C0=C4=1,表示反馈连接。因为m序列是由循环序列发生器产生的,因此C0和C4一定为1,即参与反馈,反馈系数C1为1,参与反馈;C2,C3为0,则反馈线断开,即表示无反馈连线,可以得到4级移位寄存器构成的循环序列发生器模型如图1所示,其中反馈系数为反馈信号的抽头系数。
寄存器的状态决定于时钟脉冲控制下输入的信息(“0”或“1”),第4级移位寄存器决定于前一时钟脉冲后的第3级移位寄存器状态。参加反馈的各级输出经多次模2和后把最后结果输入第一级。对应的特征多项式(2)应为:
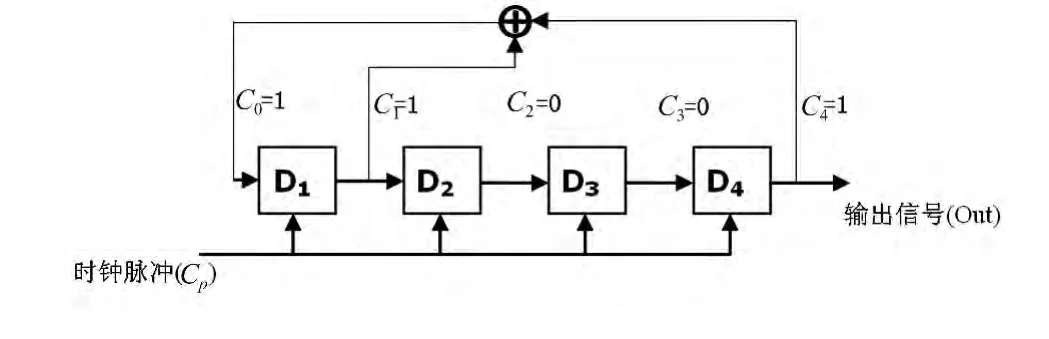
图1 4级循环序列发生器模型


表1 n=4的m序列发生器状态值
由表1可知,移位寄存器产生的4级 m序列:100011110101100,将其循环左移4比特后的码序列为:111101011001000
2 基于SystemView的4级移位寄存器仿真模型设计
2.1 基于SystemView的m序列发生器仿真模型功能框图设计
根据4级循环序列发生器模型的基本原理,将各部分功能模块化,然后找出各部分之间的关系,确定系统框图,如图2所示为m序列发生器系统的框图。

图2 m序列发生器系统框图
2.2 基于SystemView的4级移位寄存器模型的仿真电路设计
运用SystemView仿真平台的信号源库、通信库、信号观察窗库等模块功能[14-16],对m序列生成器系统进行电路仿真设计。因为该模型中,通信图符库中的PN序列产生器图符要求输入一定频率的时钟信号,并设定相应的移位寄存器长度、反馈系数及起始种子等参数可得到所需的PN序列,所以依据循环序列生成器工作的基本规律,按照生成器系统框图的功能,找出各部分功能模块之间的关系,搭建4级 m序列生成器模型的系统电路如图3所示。如表2所示,设置m序列生成器系统仿真电路模型中各图符块的参数。

图3 4级序列生成器系统电路

表2 各功能模块参数表
3 仿真及分析
SystemView提供了一个真实而灵活的窗口用以观察、分析系统波形。首先,设置时间窗口参数:Start Time(sec):0,Time Spacing(sec):300e-6,No.of Samples:512,No.of System Loops:1,其次,运行仿真系统,则在系统分析窗口中观察到钟脉冲(Cp)和4级m序列波形的仿真结果分别如图4、5所示。

图4 时钟脉冲波形

图5 4级m序列波形
从图4、5的对比观察可直观地得到:15个时钟周期的脉冲经4级序列生成器产生一个15位的m序列,即n取4,则P=2n-1=15个时钟周期为周期的循环序列,即TP=0.15 s=15 TCp。反馈移位寄存器组成的环形计数器产生的m序列为111101011001000,由图5可观察到15位m序列的结果与理论分析相符合。
如图1所示的4级m序列发生器。假设初始状态为(D1D2D3D4)=(0001),在时钟脉冲的作用下,逐次移位。D1⊕D4作为D1输入,则n=4的码序列产生状态过程如表1所示。
4 结束语
本研究通过对m序列的数学模型分析研究,借助于System View仿真软件,设计实现了4级15位m序列的电路,实验结果表明,设计电路合理,仿真结果与理论分析相一致。依据被研究的真实模型,利用电子仿真软件构建被对象系统的仿真模型,进行电路设计、仿真、调试,完成通常在相应硬件实验室才可以完成的实验,比较真实地描述系统的运行、演变及其发展过程。该方法为以后的其他相关研究提供了理论和实验基础。本文所做的工作对深入分析和促进PN序列的工程应用具有重要的意义。
[1]于超鹏,郝亮飞,谢金华.线性调频和巴克码组合调制雷达信号[J].探测与控制学报,2009,31(5):20-24.
[2]杨帆,杨烨,李国平,等.基于AT89S52的温度测控系统设计[J].电气自动化,2009,31(3):53-54.
[3]李向军,李静.巴克码序列在目标探测技术中的应用[J].西安工程科技学院学报,2004,18(4):417-419.
[4]吴明捷,杜天苍.伪随机码及计算机的产生[J].辽宁工程技术大学学报:自然科学版,2002,21(2):203-206.
[5]徐庆,徐继麟,周先敏,等.线性调频二相编码雷达信号分析[J].系统工程与电子技术,2000,22(12):7-8.
[6]王会华,李宝平.m序列发生器的设计与实现[J].北京电子科技学院学报,2007,15(2):58-61.
[7]李栋,刘进江.m序列的MATLAB仿真与实现[J].重庆工学院学报:自然科学版,2008,22(4):139-141+159.
[8]程受浩,徐德华,刘华.随机二元码调相连续波信号分析与波形设计[J].探测与控制学报,2002,24(4):7-9.
[9]曹志刚,钱亚生.现代通信原理[M].北京:清华大学出版社,1992.
[10]林秀鼎.m序列自相关系数的递推算法[J].应用数学学报,1984,7(2):133-141.
[11]朱士信.产生m序列的一个递推算法[J].通信保密,1995,63(3):75-77.
[12]章照止,罗乔林.产生m序列的一个递推算法[J].系统科学与数学,1987,7(4):335-343.
[13]郭梯云,杨家玮,李建东.数字移动通信[M].北京:人民邮电出版社,2005.
[14]王傲.易白年.信号波形合成分解的设计与实现[J].电气自动化,2013,35(3):24-26.
[15]陈军,李春光.具有自适应反馈突触的神经元模型中的混沌:电路设计[J].物理学报,2011,60(5):5031-5037.
[16]陈军.基于System View的数字基带传输系统模型设计与分析[J].实验室研究与探索,2013,32(10):98-101.

