可靠性理论在丁坝稳定分析中的应用探讨

牟萍，王平义，韩林峰

（重庆交通大学国家内河航道整治工程技术研究中心，重庆交通大学省部共建水利水运工程教育部重点实验室，重庆 400074）

0 引言

航道整治的成败关键在于治理效果，而整治建筑物的稳定性是确保治理效果的重要基础。工程经验、模型试验和数值模拟为整治建筑物的水毁机理及水沙运动规律等问题的研究提供了有效手段，并取得了一定成果[1-6]。

然而对整治建筑物的稳定性计算公式，现有规范多为经验公式，缺少理论的受力分析和破坏机理，除此之外对整治建筑物结构受力稳定及水毁程度量化计算方面的研究相对较少[7]。目前，对整治建筑物稳定性分析通常采用基于经验的单一安全系数法，这种方法最大的缺点是未考虑模型和参数的不确定性，不能全面准确地反映整治建筑物的可靠性。

可靠度理论和方法广泛应用于土木、水利等领域的结构工程分析设计[8-9]。与岩土、土木、水利等建筑物破坏形式不同，受内外因素的相互影响，航道整治建筑物破坏因素极为复杂[10]：一方面，航道整治建筑物大多密实度较差、结构强度低、基础的可动性强；另一方面，水流、河势等外部作用因素变化剧烈，加之整治建筑物通常位于水下，环境复杂且难以进行实际观测。正是由于整治建筑物水毁破坏受众多不确定因素的影响，人们对整治建筑物水毁机理的认识深度还不够，可靠性理论计算方法在整治建筑物稳定性分析的应用缺乏必要的理论基础，国内外航道整治工程领域尚未形成公认的整治建筑物失稳破坏的计算模型及相关参数的确定方法[11]。

本文在航道整治建筑物现状调查的基础上，分析了整治建筑物抛石丁坝水毁的机理和影响水毁的不确定性因素，建立了抛石块体的稳定性计算模型，推导了丁坝可靠性功能函数和极限状态方程。

1 整治建筑物现状调查

通过对荆江河段和上下游类似航道坝体整治建筑物近年损毁维修资料的整理分析，2006—2013年，荆江河段出现破坏的3处坝体中多数为丁坝，顺格坝损毁1处，见表1。

表1 荆江河段已建坝体损毁情况表Table 1 The damage of built dike in Jingjiang reach

结合近年长江中下游其他水道坝体类航道整治建筑物损毁及维修情况，如界牌出现损毁坝体12处，维修8座；张南水道出现损毁坝体6处，维修7座；武穴水道损毁维修记录等资料，坝体损坏主要包括坝头破坏（图1）、坝身破坏（图2）、坝根破坏和坝面破坏（图3）4种形式。

图1 坝头破坏Fig.1 Dam head damage

图2 坝身破坏Fig.2 Dam body damage

图3 坝面块石流失、沙枕出露Fig.3 Block stone lossand sand pillow exposed on the dam surface

发生水毁的原因可以归纳为两类，一是由于自然环境的变化，主要表现为在水沙的相互作用下，坝头、坝根等部位存在较大水流流速梯度、紊动、脉冲等现象，对坝体及基础的受力均产生影响；二是人为因素，主要表现为大规模的采沙活动改变了原有的水沙环境，过渡围河造地破坏了天然河流系统的平衡条件，以及人类修建的各种涉水建筑物，它们之间通过改变水沙环境，彼此相互影响。

2 整治建筑物稳定性评价中的不确定性分析

随着科学技术的进步和航道整治理论研究的深入，人们意识到传统的单一定值稳定性分析中还存在许多不确定性因素，主要因为理论分析和测验技术两个方面存在不确定性，表现在对整治建筑物计算模型选取的合理性上和对所选用材料强度参数测定的精确性上。因此，在完善整治建筑物稳定性评价时，应将这些不确定性因素考虑进去。按照工程背景分类，整治建筑物不确定因素体现在以下5个方面：

1）荷载作用的不确定性。由于整治建筑物大多密实度较差，而且水流条件与河道地势变化频剧，因此很难找出适合的作用在整治建筑物上的荷载的具体计算式及其组合方式，并且水流作用及泥沙运动本身具有一定的随机性和不确定性，使得对其水毁机理的认识往往不够深入，因此整治建筑物水毁过程中所受的荷载带有明显的随机性和不确定性。

2）材料参数的不确定性。土石性材料参数的不确定性十分明显，首先在于岩土材料本身在空间和时间上的可变性。以丁坝为例，大多以抛石为主，密实度较差、结构强度低、基础可动性强，在空间各个方向都有可能发生较强烈变形，而且由于是散抛石结构，在块石材料的选择上、抛填质量上及结构空间密实度上都存在着较大差异。另外由于在室内或现场试验存在的误差、石体材料随时间发生老化等，都会导致材料参数的不确定性。

3）初始条件和边界条件的不确定性。无论是应力场、流场还是渗流场的计算，都会有边界条件的影响，对于动力问题或非稳定问题，初始条件的影响也不容忽视。而边界条件的不确定性来源于实际问题的复杂性、边界变化的不可预知性、人类认识局限性以及对结构边界处理的简化等，初始条件往往由于人们对问题考虑的不够全面而忽略了一些对结果影响较大的因素。

4）人为因素的不确定性。在施工阶段，施工质量的好坏以及人们选址、设计的优劣都会对整治建筑物建成投入使用的寿命带来影响。在整治建筑物使用阶段，由于人为因素整治建筑物遭到破坏以及是否及时有效地对整治建筑物进行维护，这些都给建筑物的稳定带来不确定性。

5）计算模型的不确定性。由于实际工程的复杂性，一般情况下，可根据模型试验、工程地质资料甚至工程经验来初步确定建筑物稳定计算模型，但符合选模原则的最佳模型只有1个，这正是模型识别的工程背景。事实上，不论采用哪种本构模型和强度准则都不可能绝对地反映材料的本构关系和破坏特性，因此选择模型很大程度上是一个模糊的概念。

3 丁坝可靠性分析的基本原理

3.1 整治建筑物设计使用年限的确定

结合航道整治工程的本质，航道整治建筑物可靠度作出如下的定义：整治建筑物可靠度为在规定的设计使用年限内，在一定的水流、边界条件下，建筑物结构满足整治要求的概率。其中设计使用年限为结构或构件不需进行大修即可按其预定目的使用的时段，结构的设计使用年限需要考虑结构的形式、使用目的、使用环境及维修的难易程度、费用和重要性等。根据表2规定的不同结构设计使用年限以及考虑到实际情况下整治建筑物应起到的作用，将整治建筑物的使用年限规定为10 a以内。

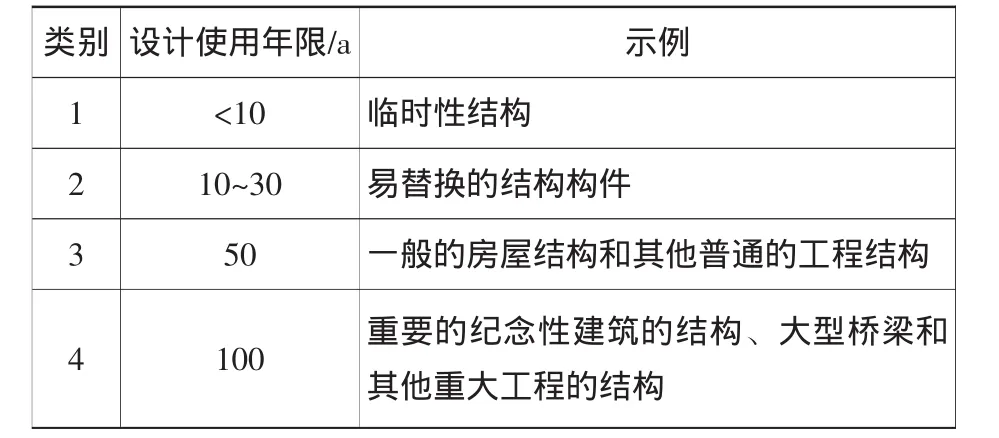
表2 我国GB 50153—2008《工程结构可靠度设计统一标准》规定的结构设计使用年限Table 2 The structuraldesign working life regulated by GB 50153—2008Unified standard for reliability design of building structure

到目前为止，航道部门尚未制定整治建筑物使用年限的标准，本文之所以将10 a定为其设计使用年限，是考虑到以特大洪水发生的概率来定的。作为设计人员，希望经一般洪水作用后整治建筑物通过简单修复可以继续使用。而经特大洪水作用时，即使事先有所防范，但产生的结果有时仍是无法预测的。而且当特大洪水发生时整个河道的河势与地形都会发生改变，到时应审时度势，有时甚至要放弃原有航道另辟蹊径。所以，如果前期在整治建筑物的结构加固上投入过多的人力物力，一来由于无法准确判断未来河道可能发生的走势，前期投入过多难免造成浪费；再者，如果将来另辟出一条更加有利的航道或原航道主支汊发生转变，原有的整治建筑物也不利于航道的变通。

综上考虑，将设计使用年限定为10 a，既能在较长的时间内满足河道的通航条件，又能在出现重大抉择时随机应变。

3.2 抛石丁坝坝面块石受力分析

丁坝坝面的几何形态一般都是以梯形断面为主。当洪水期水流漫过坝顶时，丁坝背水坡面护石就成了丁坝坝体结构的一个软肋。护面块石往往在过坝水流与坝后水面相交处被掀起形成缺口，该处水流流态紊乱，脉动压力较大。

丁坝坝体坡面一般较陡，所以要考虑块石自重沿水流方向的分力。假设有一倾角为α的斜坡面，水流沿与斜面水平的方向流动，块石在斜面上的受力如图4所示。

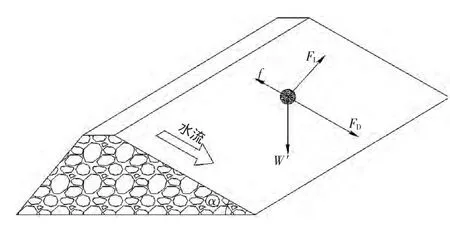
图4 坡面上块石受力示意图Fig.4 The stressof blockson the slope

图4 是淹没式丁坝坝体背水坡面护体块石的受力情况。图4中：α为护体块石所在坝体位置的几何坡度；f为护体块石的运动阻力，包括摩擦力与石块间的阻挡力；FL为水流上举力；FD为水流拖曳力与动水冲击力的合力，为表达方便，简称水流推拖力。淹没式丁坝有坝顶漫流，坝体背水坡面护体块石所受水流推拖力的方向与块石水下重力分力方向几乎相同，根据二力合成性质，可知二者合力最大。阻力f大小受上举力FL的影响，FL越大，阻力f就越小，石块就越不稳定。在漫坝水流与坝后水面相交位置的水流脉动压力很大，上举力FL的值很大，所以，此处稳定性很差。

由于水流动水冲击力的矢量方向是随机的，与石块形状有关，这里以理想球体代表石块，所以石块所受动水冲击力方向与水流拖曳力方向相同，为表达方便，图中水流拖曳力与动水冲击力的合力用同一符号FD表示。拖拽力和上举力的一般表达形式为：

式中：ρ为水的密度，1 000 kg/m3；u0为水流底速，m/s；d为块体粒径，mm；CD为阻力系数；CL为上举力系数；a1，a2为面积系数，对于球体，a1，a2= π/4。

3.3 极限方程的建立

丁坝的水毁主要是坝头、坝顶（包括背水坡）及坝根的破坏，为了对丁坝进行可靠度分析，首先必须建立坝体稳定可靠性分析功能函数，在定值法分析计算的基础上，选定某些参数为基本变量，并令按定值法计算得到的安全系数K=l，则可得到相应于各种分析方法的功能函数及极限状态方程。可靠性分析是建立在极限平衡分析的基础上进行的，应用何种分析方法将十分关键。由于丁坝大多采用抛石结构，所以本文对丁坝坝坡的稳定性分析拟参考无黏性土坡稳定分析方法，并结合有渗流作用时的无黏性土土坡稳定计算公式，此种方法计算不很复杂，且精度较高。

库区蓄水或洪水期水位上涨，都会使抛石丁坝受到一定的渗流力作用，对坝体稳定性带来不利影响。此时在坝坡面上渗流逸出处以下取一单元体，它除了本身重量外，还受到渗流力J的作用。因渗流方向与坡面平行，渗流力的方向也与坡面平行，此时块石下滑的剪切力为：

考虑到上一节坝面块体稳定性分析中提到的上举力与水流推力，将其与块石剪切力联系起来可得到块石沿斜坡下滑所受到的合力为:

式中：α为背水坡坡角；φ为块石内摩擦角；J为渗流力；W′为单元体有效重力。

对于抛石块体来说，当直接用渗流力来考虑渗流影响时，单位体积的块体自重就是浮重度γ′，而单位体积的渗流力j=iγw，式中γw为水的重度，i则是考虑点的水力梯度。因为是顺坡出流，i=sinα，于是上式可写成：

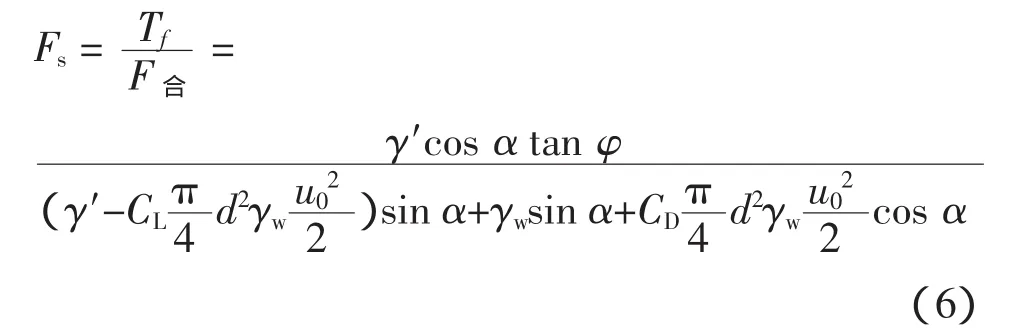
化简后得：

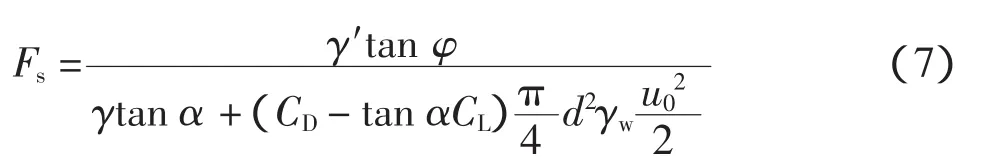
由式（7）所示的有渗流作用时的丁坝坝体稳定计算公式，假定边坡属于极限平衡状态，令Fs=1，于是得到极限状态方程：

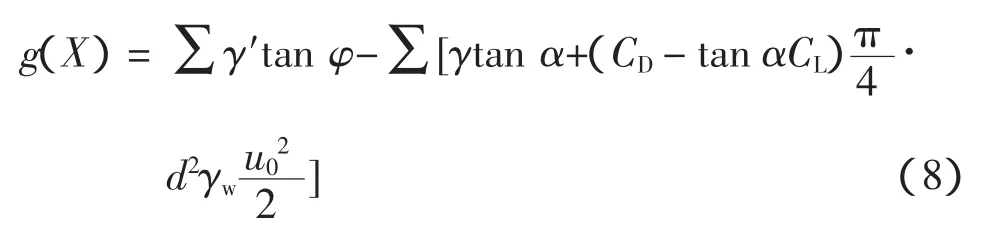
其中γ为块石的重度，应用可靠度理论于丁坝稳定问题时应首先确定基本随机变量，这些基本变量可以是几何尺寸、材料性能指标和作用荷载等。式（8）中α﹑γ和γw等可视为常数，因此只要知道参数CD、CL、φ的分布模型，继而可以通过式（8）对抛石坝坝体可靠度进行计算。根据可靠性理论，当g（X）＞0时，坝体处于稳定状态；当g（X）＜0时，坝体处于不稳定状态；当g（X）=0时，坝体处于临界状态。

找寻CD、CL、φ的分布规律需研究其统计方法、统计特性以及参数取值等问题，而目前对丁坝可靠度的研究尚处在起步阶段，对于参数CD、CL、φ的研究还需要大量的实测资料以便归纳出其分布规律，以进一步对丁坝可靠度进行计算。

4 结语

由于试验、量测技术等的限制，本文基于一些假设，对丁坝可靠性功能函数及极限状态方程进行了推导，并且推导过程中进行了适当简化。然而实际中受水流、泥沙、边界条件的影响，丁坝坝体的受力过程是一个复杂的随机过程，并且丁坝坝体的抗力变化受材料强度、变形以及环境的影响，其可靠度要复杂得多。模型中的一些参数要根据试验或经验取值，因此对模型中相关参数进行试验或实测是今后工作的重点。

[1]OHMOTO Terunori,HIRAKAWA Ryuichi,WATANABE Kunitoshi.Effects of spur dike directions on river bed forms and flow structures[J].JournalofApplied Mechanics,2005(8):875-882.

[2] YU Tao,WANG Ping-yi,YANG Cheng-yu,et al.Experimental

study of water force acting on spur dike[C]//ZHAO Jing-ying.Advanced materials research.Switzerland:Trans Tech Publications,2011,255-260:3 558-3 562.

[3] HOSSEIN Azinfar,JAMESA Kells.Flow resistance due to a single spur dike in an open channel[J].Journal of Hydraulic Research,2009,47(6):755-763.

[4]韩林峰，王平义，刘怀汉，等.洪水作用下丁坝可靠度分析及剩余寿命预测[J].水利水运工程学报，2013（6）：54-60.HAN Lin-feng,WANG Ping-yi,LIU Huai-han,et al.Analysis of spur dike reliability by theaction of flood and evaluation of residual life.Hydro-Scienceand Engineering,2013(6):54-60.

[5] 应强，曹民雄，邢素英.丁坝坝头冲刷坑深度的研究[J].南昌水专学报，1999，18（1）:16-20.YING Qiang,CAO Min-xiong,XING Su-ying.A study on the local-scourholesatgroin-nose[J].Journal of Nanchang College of Water Conservancyand Hydroelectric Power,1999,18(1):16-20.

[6] 周银军，陈立，刘金，等.桩式丁坝局部冲刷深度试验研究[J].应用基础与工程科学学报，2010，18（5）:750-758.ZHOU Yin-jun,CHEN Li,LIU Jin,et al.Experimental study on localscouring depth ofpermeable pile groin[J].Journal of Basic Scienceand Engineering,2010,18(5):750-758.

[7] 喻涛.非恒定流条件下丁坝水力特性及冲刷机理研究[D].重庆:重庆交通大学，2013.YU Tao.Studyon hydraulic characteristicsand scourmechanism of spur dike in unsteady flow[D].Chongqing:Chongqing Jiaotong University,2013.

[8] 王平义，程昌华，荣学文，等.航道整治建筑物水毁理论及模拟技术[M].北京：人民交通出版社，2005.WANGPing-yi,CHENGChang-hua,RONGXue-wen,etal.Water damage theory and simulation technology ofwaterway regulating structures[M].Beijing:ChinaCommunications Press,2005.

[9] 解中柱.航道整治建筑物可靠性设计的思考[J].中国港湾建设，2008（3）：36-37.XIE Zhong-zhu.Considerations in reliability design of waterway regulating structures[J].China Harbour Engineering,2008(3):36-37.

[10]张世明，张荣坤.重力式挡土墙结构可靠度计算方法[J].东北水利水电，2013（3）：20-23.ZHANG Shi-ming,ZHANG Rong-kun.Reliability calculation method ofgravity retainingwall[J].Water Resources&Hydropower ofNortheastChina,2013(3):20-23.

[11]XU Ge-ning,YANG Rui-gang,ZHOU Ke,et al.Methodology to estimate remaining service life of steel structure by possibilistic reliability theory[J].Chinese Journal of Mechanical Engineering,2010,23(6):780-787.