基于非线性有限元法的二维水下拖缆研究

邵 校，刘祚秋

（中山大学应用力学与工程系，广东广州 510275）

0 引言

拖曳系统通常由拖曳电缆、拖曳体及专用绞车组成,拖曳体内可根据不同的用途搭载温、盐、压、营养盐及声纳等各种海洋化学元素探测传感器或声、光等物理探测传感器。拖曳船上的操作者可以通过一定的控制方式实施对拖曳体的轨迹与姿态控缆作为整个系统的重要组成部分，起着连接拖曳母船（潜艇）与拖体设备的作用，它具有远距离传输能源和信号的能力，并为水下设备提供前进的动力。

国内外学者对此进行了广泛而深入的研究，目前描述拖缆的理论方法大致可分为[3-4]：解析法[5]、有限元法[6-7]、集中质量法[8]、有限差分法[9]。解析法是指那种可以给出封闭解的理论模型,由于该模型只能局限于求解简单的静态问题,其使用范围有限；集中质量法是将缆索视为由一系列无质量弹簧连接着离散的集中质量点。顾懋祥等人[10]的计算经验表明：在使用集中质量法时，缆绳模型分段太多将引起数值发散；有限差分法和集中质量法在应用过程中受到一些限制，且在强几何非线性和材料非线性问题上计算不易控制；基于小变形线弹性理论的线性有限元法忽略了缆索的及和非线性和材料非线性，在实际缆索计算中存在误差。

为了克服其他计算方法的不足，本文采用非线性有限元方法计算缆索几何形态及受力特性，考虑了缆索的各种受力及缆索的弹性变形，可有效对拖曳模型进行模拟。通过Matlab语言，设计非线性有限元算法程序，结合悬链线法能使计算结果较快收敛。

图1 水下拖缆模型

1 拖缆模型计算

如图1中所示，由于缆索运动机理非常复杂，故作如下假设：1）忽略波浪对拖体设备的作用；2）只考虑在材料的线弹性阶段工作，即索始终处于弹性工作阶段，符合虎克定律；3）索是一维体；4）索是理想柔性的，只受拉力而不能受压和抗弯；5）大位移小应变。

1.1 悬链线方程

悬链线方法对松弛的（有剩余索链躺在水底的）和张紧的（索链全部提起其下端拉力倾斜的）两种状态都适用。由于张紧状态悬链线适用范围更广，因此本文着重讨论张紧式悬链线。为便于公式推导，分别建立笛卡尔坐标系及拉格朗日坐标系。以缆索右下端为原点定义笛卡尔坐标系。以缆索右下端为原点定义为缆索弧坐标。

图2 静水中缆索受力示意图

如图2所示使用截断法推导悬链线方程，S0、Sd分别表示自然无伸张状态，动态缆索的弧坐标。区间[0,l]上静水中缆索只受端部力与重力的作用如图1所示，S0=l处拉力为其中，水平方向的分量Th=Th0-Rwx，竖直方向分量Tv=Tv0+(W-B)-Rwy；Th0和Tv0分别为S0=0处作用在缆索上的水平力和竖直力，对于张紧状态悬链线有：Tv0＞0。

缆索的拉格朗日应变为：ε=(dsd-ds0)/ds0，即：dsd=(1+ε)ds0，s0=l处缆索微段与x轴正方向的夹角为ϕ，那么：

以缆索微段切线方向与法线方向为坐标轴建立局部坐标系，如图3。为简化计算将海水与缆索之间的相对速度vr视做匀速且只有水平方向的相对速度。那么缆索微段与水流切向相对速度vrτ、缆索微段与水流法向相对速度vrn分别为：

图3 缆索微段受力示意图

根据水动力学Morison公式，流体施于微段缆索上的作用力为（图3中所示）：

式中：ρw为海水密度；D为缆索直径；CDτ、CDn分别为缆索微段切向和法向阻力系数。

将求出的fτ、fn再转化到整体坐标系下，结合式（1）即可得到：

在区间[0,s]上，缆索在水中的净重：

式中：ρc为缆索在空气中的密度；A为缆索横截面积；g为重力加速度。若不考虑材料非线性，则：式中：E为弹性模量，A为缆索横截面积。将以上各式代入方程的积分形式便可得到缆索各点的横纵坐标：

在区间[0,l]上取定积分可得：

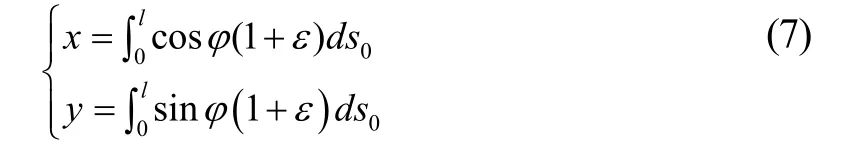
显然，这种情况下缆索的控制方程为非线性，无法求得解析解。为简化计算，令vr=0（即，使缆索处于静水中），积分后可得下式：

1.2 非线性有限元基本方程

由上述推导过程不难看出拖曳缆索表现出很强的几何非线性，在外部荷载作用下缆索产生大位移但应变仍然很小，其应力应变关系仍处于弹性范围内[11]，其平衡方程无解析解，须采用数值方法进行计算。

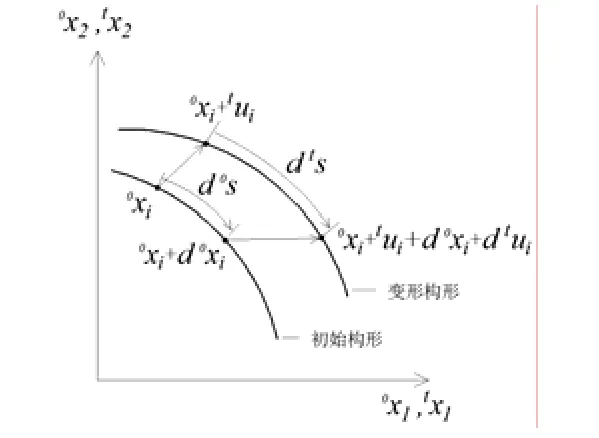
图4 缆索单元构形及变形构形

根据虚位移原理采用完全拉格朗日表述，推导得到连续体增量运动平衡方程[12]：

式中：

在大位移小应变的假定下，柔性索单元的应变ε只需考虑格林应变的第一项，即：

以上各式中：E为弹性模量；ρc为缆索密度；为时间t+Δt时刻的加速度；为第二类Piola-Kirchhoff应力；和分别是Green应变张量增量的线性项和二次项；时间t+Δt位形外力所做的虚功；为t时刻增量位移；为t时刻坐标。

本文采用二节点索单元离散缆索，依照等参变换的概念，可直接得到单元节点坐标向量及单元节点位移向量，各式有如下关系：

式中：[N]为插值形函数矩阵。忽略惯性项推导出拖曳缆索平衡方程：

在应用有限元方法时需将作用在缆索上的水流力等效地作用在单元节点上。假定水流力所做的功为：

如图3及所示，将式(3)代入式(25)可得：

1.3 非线性有限元方程求解方法

解决非线性有限元问题常常使到

Newton-Raphson迭代法（N-R法）或修正的

Newton-Raphson迭代法（mN-R法）[13]，为了更好地得到收敛结果，这里使用N-R法。使用迭代法求解非线性问题需要给定初始节点坐标，若采用偏离真实值的较远的时极容易导致迭代，发散或漂移。使用上述的悬链线方程即可求得较好。计算的基本步骤为：1）假定缆索初始张力Th0、Tv0，使用本文中的悬链线法求得缆索上节点坐标向量并假定缆索初始位移为零；2）将代入非线性有限元解法中进行N-R迭代，直至收敛。

2 数值算例

为了验证本方法对拖曳缆索研究的适用性。以拖船端为拖缆起始端，分别取航速为3kn、5kn、7kn、9kn、11kn、13kn、15kn、17kn和19kn来模拟拖缆形态，计算缆索张力并作出缆索收敛图。拖缆各参数如下表：

表1 拖缆及拖曳体参数

以(xi,yi)为坐标做收敛图（见图5）观察其收敛性。ne为单元个数，其中：

式中[U]为节点位移增量向量；[Ψ]为节点不平衡力向量。

图5 各航速收敛图

由图5可以看出以(xi,yi)为坐标的点随着迭代步数的增长都落在在了收敛区（虚线矩形框内），说明本文设计的方法收敛性较好。随后将各航速下拖缆形态及受力情况做了对比（如图6和图7）。

图6 不同航速缆索形态图

图7 不同航速缆索张力图

由图6和图7可知虽然拖缆的形态及受力情况在不同航速条件下很大差别，但也呈现出一定的连续性。

3 结语

1）近年来非线性有限元方法常用于海洋系泊缆索的理论研究，本文将非线性有限元法配合悬链线法应用于拖曳缆索的研究达到了较为理想的效果。以悬链线法的结果作为Newton-Raphson迭代法的初始节点坐标能达到较好的收敛效果。

2）航速会影响拖曳体水平力与竖向力的比值进而影响缆形，忽略拖缆振动情况下，在拖船匀速行驶时拖缆呈现相对固定形态。

3）随航速的递增缆索张力越呈现非线性增长，增长越缓慢，在航速较大时，航速对拖缆张力影响不大。

[1]吴家鸣, 叶家玮, 李宁.拖曳式多参数剖面测量系统水动力与控制性能研究述评[J].海洋工程,2004.22(1):111-120.

[2]王飞.海洋勘探拖曳系统运动仿真与控制技术研究[D].上海: 上海交通大学,2007.

[3]Vineetk.Srivastava.Analyzing Parabolic Profile Path for Underwater Towed-Cable[J].Journal of Marine Science and application, 2014, 02: 185-192.

[4]张攀.拖曳系统仿真计算[D].武汉:武汉理工大学,2005.

[5]Irvine H.M, Caughey T.K.The linear theory of free vibrations of a suspended cable[A].Proceedings of royal society of London, series A, 1974, 341: 299 -315.

[6]Leonard J W, Recher W W.Nonlinear dynamics of cables with low initial tension[J].Journal of the Engineering Mechanics Division, ASCE.1972, 98 (EM 2): 293 -309.

[7]Ma David, Leonard John, Chu Kuang-Han.Slack-elasto-plastic dynamics of cable systems[J].Journal of the EngineeringMechanics Division ASCE.1979, 105 (EM2):207 -222.

[8]Walton T.S, Polacheck H.Calculation of transient motion of submerged cables.Mathematics of Computation,1960, 14, 27-46.

[9]Ablow C M, Schechter S.Numerical simulation of undersea cable dynamics.Ocean Engineering, 1983,10(6),443-457.

[10]顾懋祥,邵建南.拖曳系统动力学计算[J].舰船性能研究, 1988, (3): 31-43.

[11]杨敏冬, 滕斌, 勾莹，姜胜超.海洋系泊缆索非线性有限元静力分析[J].海洋工程, 2009,27(2):14-20.

[12]Bathe K J.Finite element procedure[M].Englewood Cliffs: Prentice-hall, 1996.

[13]王兴刚, 深海浮式结构物与其系泊缆索的耦合动力分析[D].大连: 大连理工大学, 2011.