船舶上层建筑重量重心对其固有频率的影响

王 墨，马 骏

（大连理工大学船舶工程学院，辽宁大连 116024）

0 引言

影响船舶上层建筑首阶固有频率的因素有很多，如上层建筑自身总体刚度、上层建筑根部支撑的刚度、上层建筑重量大小及重心位置等。人们试图分析和总结各种因素对上层建筑固有频率影响的大小，在此过程中逐渐引入了灵敏度分析的方法。灵敏度分析是研究模型的输入和输出间的关系的一种分析方法，用于定性或定量地研究不同的模型输入对模型的输出的影响以及模型对输入的依赖程度。过去在对上层建筑首阶固有频率进行估算时根据上层建筑的主要尺度使用基于统计数据和回归分析的经验公式估算[1-3]。但是这些经验公式提出时间较早，适用船型均为排水量较小的船型，没有完全体现出上层建筑整体刚性和质量分布影响，对现代超大型船舶的计算精确度仍需探讨[4]。随着有限元计算方法的完善和计算机计算能力的突飞猛进，人们逐渐利用有限元计算软件代替经验公式对大型结构进行分析计算。本文利用Ansys有限元计算软件对某 300,000 DWT级原油船上层建筑进行建模计算，讨论船舶上层建筑的重量和中心对上层建筑首阶横向和纵向固有频率影响的灵敏度。

1 分析模型

本文对一个300,000吨级的原油船建模并进行分析计算。建立的模型包括整个上层建筑结构、上层建筑后方烟囱结构以及两者下方机舱双层底以上的全部结构。

模型采用直角坐标系，其中：

原点取为基线的0站处；

X轴沿船长方向且指向艏为正；

Y轴沿船宽方向且指向左舷为正；

Z轴沿垂向且向上为正。

图1 有限元计算模型

模型中尺寸较大的横、纵向构件及所有板材以SHELL63单元建立，尺寸较小的梁及骨材等加强结构以BEAM188单元建立。上述两种单元具有拉压、扭转和弯曲能力。每种单元的每个节点均有六个自由度，包括沿x、y、z方向的线位移和绕x、y、z轴的转角。机舱和上层建筑内的设备以MASS21单元建立。

模型的材料选为屈服模量为杨氏模量为211GPa、泊松比为0.3、默认密度为7850kg/m3的普通钢。

该船的肋距为0.85m，故为方便划分网格并兼顾计算精度，定义网格大小也为0.85m。在计算上层建筑首阶固有频率时，对模型主船体的前、后截断面及双层底位置进行简支约束。模型的主要数据见表1和表2。

表1 各层甲板主要数据

表2 模型的其他主要数据

2 上层建筑重量对固有频率的影响

在对船舶上层建筑建模时，对线缆、舾装、空冷管材等物件的重量的处理一般为均布在所在处的甲板上。通过修改各层甲板的密度来调节重量和重心，可以避免改变上层建筑的结构刚度。

2.1 方案设计

讨论上层建筑重量对首阶固有频率的影响，一般通过调节上层建筑整体结构的密度的方法达到调节上层建筑的重量的目的。用这种方法可以仅改变重量而不影响重心和结构的刚度。以整体相当密度为10338kg/m3的方案作为标准对比方案(即原船数据)，另设计6组相当密度与标准方案相当密度不同的方案（3组小于相当密度、3组大于相当密度）。各方案详情见表3。

2.2 计算结果

根据上述方案对模型进行修改并计算，得到的计算结果汇总见表4。

从表4中的结果可以看出，随着上层建筑整体重量的线性增大，上层建筑首阶横向和纵向固有频率逐渐减小。

表3 各方案详情

以方案4作为标准方案时，其首阶横向频率7.87Hz与首阶纵向频率7.40Hz作为对比的标准频率。其余方案计算得到的结果均同方案4中的结果对比。为了能更直观简洁地观察，将表4中计算结果汇总为图2和图3。

为了能更清楚地对比首阶固有频率随上层建筑总重的变化情况，把得到的计算结果同重量变化情况绘制在一张图中，见图2。其中：横向、纵向固有频率按主坐标轴（垂直）绘制，单位Hz；上层建筑总重的变化情况按次坐标轴（垂直）绘制，单位kg。图2中横轴为方案序号。

从图2中可以看出，当上层建筑总重呈线性增加时，其首阶横向、纵向固有频率均按接近线性的方式逐渐减小，固有频率变化的斜率约为重量变化斜率的一半。把上层建筑固有频率变化情况以百分比表示，绘制成图3。

表4 各方案结果

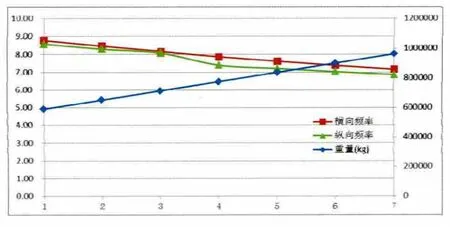
图2 上层建筑固有频率随重量变化情况

图3 上层建筑固有频率随重量变化情况（%）

图3中纵轴为变化量，以百分数表示，横轴为方案号。从这张图中可以较直观地看出上层建筑首阶横向、纵向固有频率随重量变化的情况。重量是影响上层建筑的主要因素之一，当重量改变较大时，其固有频率也有较大的变化。

3 上层建筑重心位置对固有频率的影响

除了重量会影响上层建筑的固有频率，重心位置的不同也会上层建筑的固有频率有所影响。对比重心位置不同而对固有频率产生的影响，要保证上层建筑的总重和结构刚度不变。本节中使用的方法为调节上层建筑各层甲板的密度，使总重保持不变，但重心位置的高度有所变化。

3.1 方案设计

通过调节上层建筑中各层甲板的密度来调节上层建筑整体重心位置。为此共设计了6种方案，并与方案1作对比。各方案的详情见表5。

表5 各方案详情

3.2 计算结果

根据以上各方案对模型进行修改并计算，得到的结果汇总到表6。

表6 各方案结果

将表6中的结果绘制成曲线图，见图4。

图4 上层建筑固有频率随重心变化情况

图4中横向、纵向频率曲线对应主坐标轴，单位为Hz；重心高度曲线对应次坐标轴，单位为m；横轴为方案号。

为了更清楚地对比首阶频率随重心高度位置变化的情况，把频率改变量和重心高度改变量写为百分比的形式，见图5。

图5 上层建筑固有频率随重心变化情况

图5中图中重心高度改变曲线对应主坐标轴，单位为m；横向、纵向频率改变曲线对应次坐标轴，单位为Hz；横轴为方案号。

从以上两图中可以看出，随着上层建筑整体重心的提高，上层建筑的横向和纵向首阶固有频率均有下降的趋势。横向首阶固有频率相对纵向首阶固有频率改变更大。两固有频率的改变量同上层建筑重心的改变量大致在同一个数量级。

当船舶的上层建筑较高时，可以简化地视之为一个悬臂梁。如果悬臂梁的刚度和重量不变，其重心位置越远离支点端，其固有频率越低。

4 结论

改变船舶上层建筑的重量和重心均可有效改变其首阶固有频率的大小。增大上层建筑的重量、提高上层建筑的重心均可降低其首阶固有频率，反之减小上层建筑的重量、降低上层建筑的重心可以增大其首阶固有频率。相对而言，上层建筑的固有频率对重心高度的变化更为敏感。

修改上层建筑的重心较简单，可以修改总布置挪动一些不重要的机器设备。改变上层建筑重量就相对麻烦一些，在不改变结构的前提下可以修改舾装布置，但是对总重影响不大。当通过其他方法对上层建筑重量改变较大时对整船影响也较大。所以改变上层建筑的重心是一个简单有效又可行的方法。

[1]曹迪, 赵德有, 马广宗.船舶上层建筑纵向振动固有频率估算[J].大连理工大学学报, 1989年第4期: 463-469.

[2]広渡智雪, 松本亙平, 加道博章.上部構造の前後振動に関する研究（続）[J].日本造船学会論文集, 1979, (125号): 147-155.

[3]大沼觉, 山本鹰司, 中野元博等.船尾船桥楼の船楼の振动につぃ[J].西部造船会会报, 1969, (38号): 93-120.

[4]赵德有, 林哲.船舶上层建筑整体纵向固有频率算法研究[J].中国造船.2001(03): 22-26.