基于粒子滤波的GPS定位解算方法
王家治 张璐 孙荣 樊玲

摘 要:针对GPS定位解算将非线性GPS伪距方程线性展开,产生较大定位解算误差的问题,采用粒子滤波算法定位解算伪距方程。实验结果表明,基于粒子滤波的GPS定位解算优于卡尔曼滤波,有效提高了GPS导航定位的精度和可靠性。
关键词:GPS 粒子滤波 非线性 卡尔曼滤波
中图分类号:P228 文献标识码:A 文章编号:1672-3791(2015)08(a)-0209-02
随着全球定位系统(Global Position System,简称GPS)的广泛应用,GPS动态导航和定位需求的精度和稳定性越来越高,动态范围越来越大。然而,GPS定位中存在诸多误差(测量误差和卫星位置误差)及不确定因素,极大地影响了GPS定位的精度和稳定性。
为了提高GPS定位的精度和稳定性,必须研究能有效克服误差和不确定因素影响的定位解算方法。目前GPS定位解算方法中主要采用最小二乘迭代估计算法和扩展卡尔曼滤波算法,这两种方法均需要将非线性的GPS伪距方程进行线性展开,导致定位解算误差。针对这一问题,该文采用能处理非线性、非高斯问题的粒子滤波算法定位解算伪距方程,该方法能克服误差和不确定因素的影响,进一步提高GPS导航定位的精度和可靠性。
1 粒子滤波算法
在近二十年中,粒子滤波(PF)算法被广泛应用于视频检测[1]、雷达目标跟踪[2,3]、声纳探测[4]、等领域,解决非线性非高斯模型下的贝叶斯估计问题。粒子滤波[5]算法用一组目标状态空间中的随机采样和它们对应的权值,来描述目标状态的后验PDF,其中表示权系数为的采样(粒子),表示从1时刻到时刻的状态序列,表示从1时刻到时刻的量测序列。粒子权值满足求和为1,即,因此,目标状态的后验PDF可以近似为:
(1)
其中表示Dirac函数。粒子权值的选择依据重要性采样原则[5],在假设目标运动服从一阶马尔可夫过程,并且认为量测序列相互独立的情况下,粒子权重计算公式可写为:
(2)
由于跟踪问题关心的是目标的当前状态,即在每个时刻,仅需要边缘后验PDF,而之前的状态序列可以被“边缘化”处理。因此,目标状态后验PDF可以由如下公式近似:
(3)
当粒子滤波的采样数量达到无穷大的时候,粒子滤波对后验PDF的近似将无限的接近真实[6]。
采用粒子滤波算法获得代表时刻后验概率密度函数的样本集后,目标状态的最小均方误差(MMSE)估计可写为:
(4)
2 GPS伪距单点定位原理
2.1 伪距方程
GPS伪距观测方程可表示为,
(5)
其中,表示卫星与接收机的几何距离,表示电离层延时,表示对流层延时,为接收机钟差,为卫星钟差,表示误差。电离层延时、对流层延时以及卫星钟差可通过星历、模型等方法求得,校正后的伪距为,
(6)
则,伪距观测方程可简化为,
(7)
2.2 状态模型
系统的状态方程为,
(8)
其中,接收机状态,为系统过程噪声,为系统的状态转移矩阵,
(9)
2.3 量測模型
假设接收机同时观测到颗卫星,则量测。时刻,第颗卫星的量测方程为,
(10)
其中,。
3 定位实验
该实验所使用的原始数据由NovAtel公司的OEM-615 GPS接收机输出,实验在乐山师范学院物理楼进行,天线安置在观测环境良好的楼顶。试验系统的采样频率为1Hz。另外还接收了OEM-615 接收机本身CPU计算的定位结果作为参考。基准点参考坐标采用OEM superstar GPS接收机在同一位置连续采集的24小时定位数据的平均值。
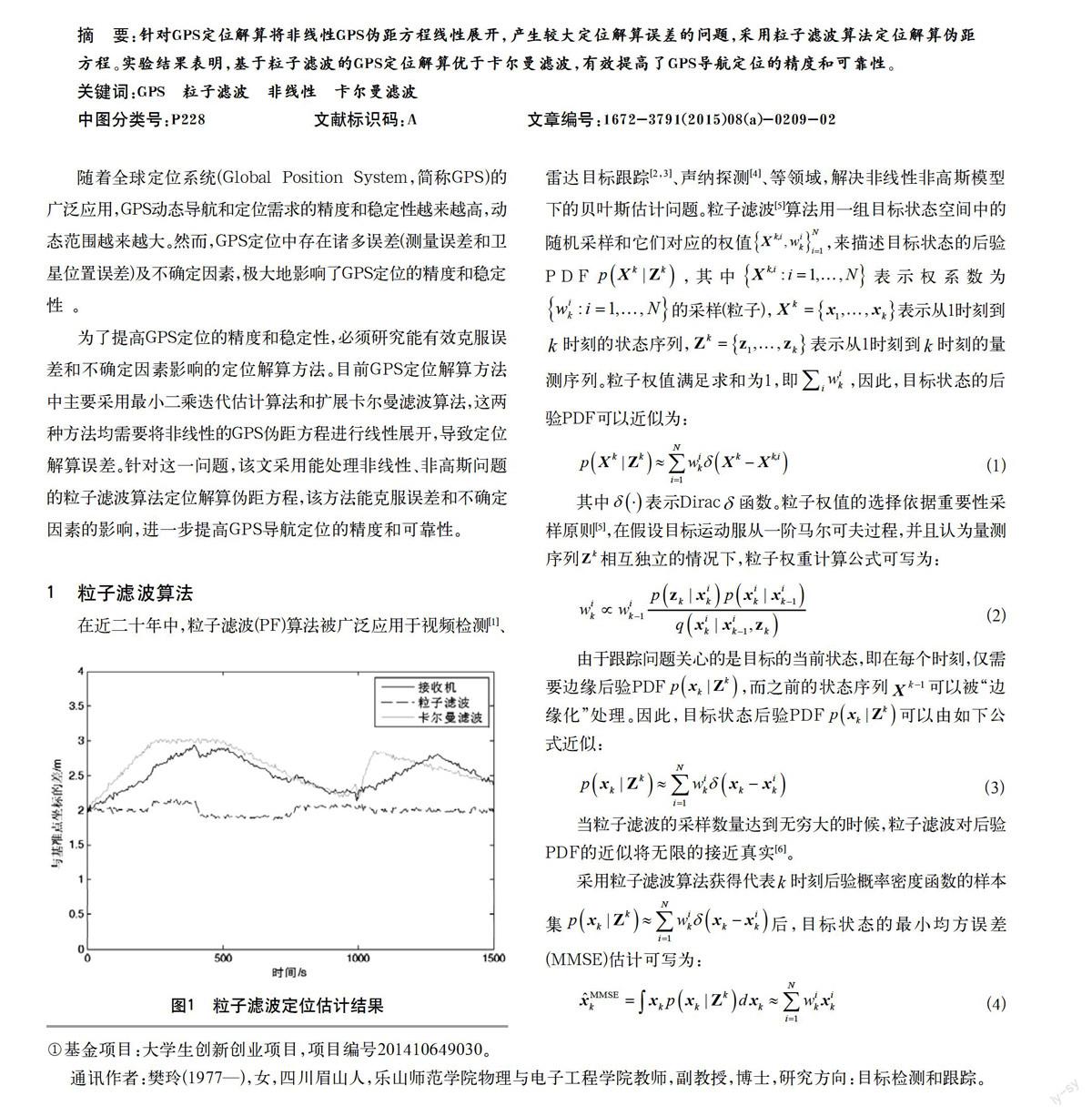
为了比较定位结果的精度,分别采用粒子滤波算法和卡尔曼滤波算法对原始数据进行了定位估计解算,定位结果如图1所示。从图1中可以看出,采用粒子滤波算法能有效抑制噪声,获得平滑的定位曲线,并且定位精度优于卡尔曼滤波算法。
4 结语
该文针对GPS定位解算将非线性GPS伪距方程线性展开,导致定位解算误差较大的问题,采用能处理非线性、非高斯问题的粒子滤波算法定位解算伪距方程。实验结果表明,基于粒子滤波的GPS定位解算优于卡尔曼滤波,进一步提高了GPS导航定位的精度和可靠性。
参考文献
[1] A.Doucet,N.J Gordon,V.Krishnamurthy.Particle filters for state estimation of jump Markov linear systems[J].IEEE Transactions on Signal Processing,2001,49(3):613-624.
[2] L.Fan,X.Zhang,and L.Wei.TBD algorithm based on improved Randomized Hough Transform for dim target detection[J].Progress In Electromagnetices Research C, 2012(31):271-285.
[3] L.Fan,X.L.Zhang,J.Shi.Track-before-detect procedures for detection of extended object[J].EURASIP Journal on Advances in Signal Processing,2011:35.
[4] A. Doucet,B.N.Vo,C.Andrieu,et al.Particle filtering for multi-target tracking and sensor management[M].Sunnyvale:Int Soc Information Fusion,2002.
[5] M.S.Arulampalam,S.Maskell,N.Gordon,et al.A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J].IEEE Transactions on Signal Processing,2002,50(2):174-188.
[6] A. Doucet,S.Godsill,C.Andrieu.On sequential Monte Carlo sampling methods for Bayesian filtering[J].Statistics and Computing,2000,10(3):197-208.

