基于重采样粒子滤波的目标跟踪算法研究
廖雪阳+任宏光+章惠君


摘要: 基于传统粒子滤波的机动目标跟踪方法针对非线性、 非高斯系统有较好的估计性能, 但是存在粒子退化现象。 利用残差重采样算法, 可以有效克服粒子滤波的退化问题。 本文针对残差重采样算法作进一步研究, 提出了一种改进的残差重采样粒子滤波算法。 该方法在残差重采样基础上进行改进, 可以避免残差重采样中关于残留粒子的重采样问题, 在保证精度的前提下提高运行效率, 减少运算复杂程度。 仿真实验结果表明该算法与残差重采样粒子滤波相比提高了目标跟踪的实时性, 并且随着粒子数的增加, 这种优势表现得更加明显。
关键词: 粒子滤波; 残差重采样; 运行效率; 目标跟踪; 粒子退化
中图分类号: TJ765; TP391.41文献标识码: A文章编号: 1673-5048(2016)05-0025-04
Abstract: The method of target tracking based on traditional particle filter performs well when estimating nonlinear/nonGaussian systems, however particles degeneration can occur. The particles degeneration can be overcome by using residual resampling algorithm. Through the research on residual resampling algorithm, an improved residual resampling particle filter algorithm is presented in this article. The method which improves the residual resampling algorithm can avoid the resampling of residual particles, thus improving running efficiency and reducing computational complexity. Simulation results show that the effect of realtime target tracking of this improved algorithm is higher than that of residual resampling particle filter. When there are more particles, the efficiency is more outstanding.
Key words: particle filter; residual resampling; running efficiency; target tracking; particle degeneration
0引言
为了解决对目标的跟踪[1]问题, 需要对目标的信息进行滤波, 当前工程中卡尔曼滤波算法应用最为广泛。 当系统为线性系统并且状态为正态分布时, 状态的期望概率密度函数依然是正态分布, 这一类估计问题可以利用卡尔曼滤波(Kalman Filter, KF)[2-3]来较好地解决。 当状态空间具有非线性或非高斯特点时, 卡尔曼滤波算法的精度会大幅下降。 采用扩展卡尔曼滤波(Extended KF, EKF)[4-5]和无迹卡尔曼滤波(Unscented KF, UKF)[6]可以解决某些形式的非线性、 非高斯条件下目标状态的估计问题。 但因为其对系统模型有很强的限制性, 需要目标的状态模型和对目标的观测模型都近似于线性, 滤波结果才有可能逼近真实状态。 针对此问题以随机采样法近似为基础的粒子滤波(Particle Filter, PF)[7-8]算法, 由于具有粒子散布特点, 可以在真值附近一定范围内迅速捕捉到真实状态, 在提高跟踪系统的收敛性和快速性方面具有较大优势[9]。
然而传统的粒子滤波存在粒子退化的不足, 即每个粒子经过多次循环计算之后, 权重的方差会不断变大, 使得很小部分后代样本的权值极大, 而绝大多数后代样本的权值却极小, 导致很多运算花费在计算影响力小的粒子上, 同时粒子也失去多样性。 当前针对粒子衰退问题, 主要的应对办法是选取更接近模型的重要密度函数和对重采样算法优化。 Gordon[10]提出了多项式重采样算法, 其核心思路是减去权值小的粒子, 将权重大的粒子留下来, 这从很大程度上解决了粒子多样性的衰退问题。 Liu[11]等人又根据多项式重采样算法提出了残差重采样算法。 由于残差重采样可以遍布到系统状态的所有粒子, 所有粒子都存在被复制的几率, 扩大了系统状态的多样性。
本文引入另一种残差重采样与粒子滤波相结合算法, 即改进的残差重采样粒子滤波(Improved Residual Resampling Particle Filter, IRRPF)算法, 其对之前的算法进行了优化, 对机动目标进行跟踪。 该算法不会产生残差重采样中的剩余粒子, 不进行二次重采样, 在保证精度的前提下减少运算次数, 从而减少时间。
1粒子滤波算法
粒子滤波[12]是一种基于蒙特卡洛仿真的滤波算法, 相对于卡尔曼滤波算法, 能更好应对各种系统的估计问题, 特别是系统的非线性度较高的情况。 粒子滤波实质是贝叶斯算法的一种表现形式, 利用状态量中一组随机样本集(粒子)来模拟真实状态的后验概率密度函数, 从而得到下一刻的状态估计。 其主要思想是利用这些采样点和权值来获得最小方差的状态估计, 是一种基于仿真的统计滤波方法。
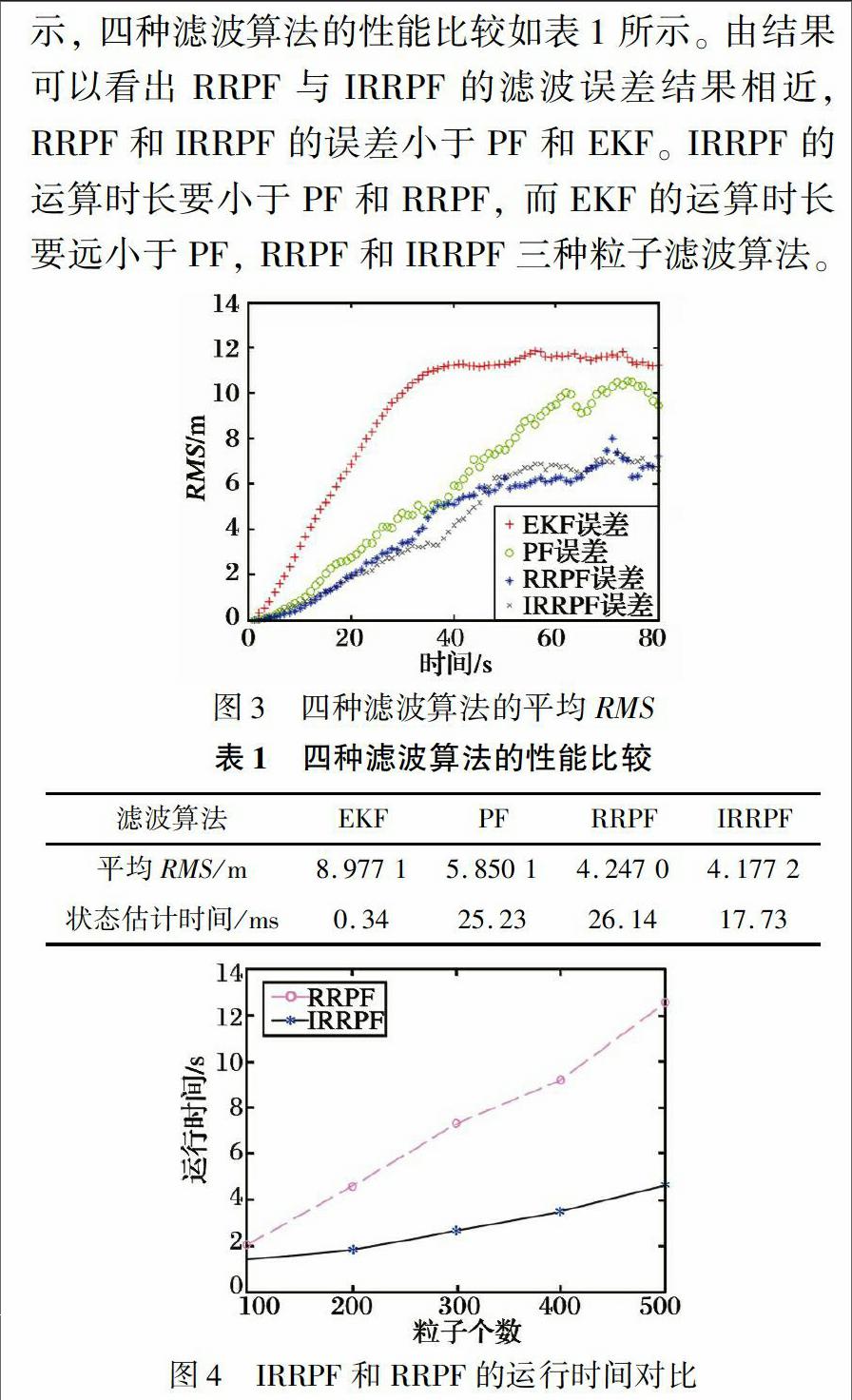
对EKF, PF, RRPF, IRRPF四种滤波算法进行100次蒙特卡洛仿真的平均RMS对比如图3所示, 四种滤波算法的性能比较如表1所示。 由结果可以看出RRPF与IRRPF的滤波误差结果相近, RRPF和IRRPF的误差小于PF和EKF。 IRRPF的运算时长要小于PF和RRPF, 而EKF的运算时长要远小于PF, RRPF和IRRPF三种粒子滤波算法。
表1四种滤波算法的性能比较滤波算法EKFPF RRPFIRRPF平均RMS/m8.977 15.850 14.247 04.177 2状态估计时间/ms0.3425.2326.1417.73不同粒子数情况下, IRRPF和RRPF的总运行时间对比如图4所示, 可见随着粒子数目的增加, IRRPF的运行效率更加突出。
4结论
在基于粒子滤波算法的目标状态估计问题中, 重采样是粒子滤波的重要步骤, 对误差结果和运行速度起重要影响。 本文针对重采样过程, 提出了一种改进残差重采样算法。 仿真结果表明, 该算法不会产生剩余粒子, 能减少运算复杂程度, 一定程度降低了运算时长, 并且当粒子数目变多时, 优化后的残差重采样粒子滤波算法相对用时更少, 效率更高。
同时也需要指出, 粒子滤波的主要优势是通用性, 相对于卡尔曼滤波算法, 粒子滤波算法必须以大量粒子为基础, 即使对其进行一些改进, 运算开销也比较大。 对于某些简单的线性或较弱的非线性问题, 卡尔曼滤波已经能达到较理想的效果, 采用粒子滤波手段所能获得的额外效果不大。 因此, 在具体应用时, 应根据需要处理问题的特点对拟采用的方法进行合理选择。
参考文献:
[1] 严运彪, 何广军, 付国庆.改进型自适应滤波算法在目标跟踪中的应用[J].航空兵器, 2008(5): 30-37.
[2] 周宏仁, 敬忠良. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991.
[3] Kalman R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Fluids Engineering, 1960, 82(1): 35-44.
[4] Sunahara Y. An Approximate Method of State Estimation for Nonlinear Dynamical Systems[J]. Journal of Fluids Engineering, 1969, 92(2): 382-397.
[5] 黄晓雷, 牛申阁.扩展卡尔曼滤波在无人机航迹控制系统中的应用研究[J].航空兵器, 2008(2): 11-17.
[6] Uhlmann J, Julier S, DurrantWhyte H F. A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators [J]. IEEE Transactions on Automatic Control, 2000, 45(3): 478-481.
[7] 朱志宇.粒子滤波算法及其应用[M].北京: 科学出版社, 2010.
[8] Cappe O, Godsill S J, Moulines E.An Overview of Existing Methods and Recent Advances in Sequential Monte Carlo[J]. Proccedings of the IEEE, 2007, 95(5): 899-924.
[9] 占荣辉, 张军.非线性滤波理论与目标跟踪应用[M] . 北京: 国防工业出版社, 2013.
[10] Gordon N J, Salmond D J, Smith A F M. Novel Approach to Nonlinear/NonGaussian Bayesian State Estimation [J]. IEE Proceedings F (Radar and Signal Processing), 1993 , 140(2): 107-113.
[11] Liu J S, Chen Rong. Sequential Montecarlo Menthods for Dynamic Systems[J]. Journal of American Statistical Association, 1998(93): 1033-1043.
[12] 吴宝成.粒子滤波重采样算法研究及其应用[M].哈尔滨: 哈尔滨工业大学出版社, 2006.
[13] 张万里, 何金刚.交互多模型的Rao-Blackwellized粒子滤波算法在多目标跟踪中的应用[J].航空兵器, 2014(4): 3-7.
[14] 黄小平, 王岩.卡尔曼滤波原理及应用[M].北京: 电子工业出版社, 2015.
[15] Van der Merwe R, De Freitas N, Doucet A,et al. The Unscented Particle Filter [M]. England: Cambridge University Press, 2000: 1-40.
[16] 王龙, 夏厚培.改进粒子滤波算法及其在目标跟踪中的应用 [J].信息技术, 2013(2): 121-123.

