差分GPS/SINS超紧组合在线标定与误差补偿方案设计

葛俊+王新龙+车欢+李群生

摘要： 为了进一步提高GPS/SINS超紧组合系统的导航和误差标定精度， 设计了一种基于载波相位差分的GPS/SINS超紧组合导航系统方案。 一方面， 超紧组合通过SINS对GPS跟踪环路的辅助， 可以降低载波环路噪声带宽， 减小码相关间隔， 提高载波环和码环的跟踪精度； 另一方面， 载波相位提供高精度量测信息作为组合导航观测量， 能够准确标定和补偿IMU常值误差， 进一步提高了组合系统的导航精度。

关键词： 捷联惯性导航系统； 全球定位系统； 载波相位差分； 在线标定； 误差补偿

中图分类号： V249.32+ 8文献标识码： A文章编号： 1673-5048（2016）05-0018-07

Abstract： In order to further improve the navigation accuracy and error calibration accuracy of the GPS/SINS ultratight integrated system， a scheme for GPS/SINS ultratight integrated navigation system based on carrier phase difference is proposed. On the one hand， by aiding GPS tracking loop with the SINS， the carrier loop noise bandwidth and the code correlator spacing are reduced， the tracking precision of carrier ring and code loop are improved. On the other hand， the high precision measurement information is provided as integrated navigation measurement by carrier phase， which can accurately calibrate and compensate the IMU error. The navigation accuracy of GPS/SINS ultratight integrated system is improved further.

Key words： SINS； GPS； carrier phase difference； online calibration； error compensation

0引言

SINS和GPS的误差特性具有较强的互补性， GPS/SINS组合导航系统集中了两者的优点[1]。 该组合导航系统根据组合深度和信息融合方式的不同可以分为松组合、 紧组合和超紧组合。 超紧组合模式通过SINS对跟踪环路的辅助能够有效消除信号中的动态， 提高接收机在高动态环境下载波跟踪性能， 同时还可以压缩环路带宽， 有效增强接收机抗干扰性能， 进一步提高组合系统导航精度和性能。 因此， 超紧组合模式成为GPS/SINS组合导航系统的最新研究方向。

提高外观测量的精度是提高组合系统导航精度和误差标定精度的有效途径， 为了在超紧组合模式的基础上进一步提高组合系统的导航和误差标定精度， 本文设计了一种基于载波相位差分的GPS/SINS超紧组合导航系统方案。 采用高精度的差分GPS信息作为观测量， 通过组合导航系统对SINS进行误差在线标定与补偿， 能够准确标定和补偿IMU常值误差， 进一步提高组合系统的导航精度。

1差分GPS/SINS超紧组合系统方案设计

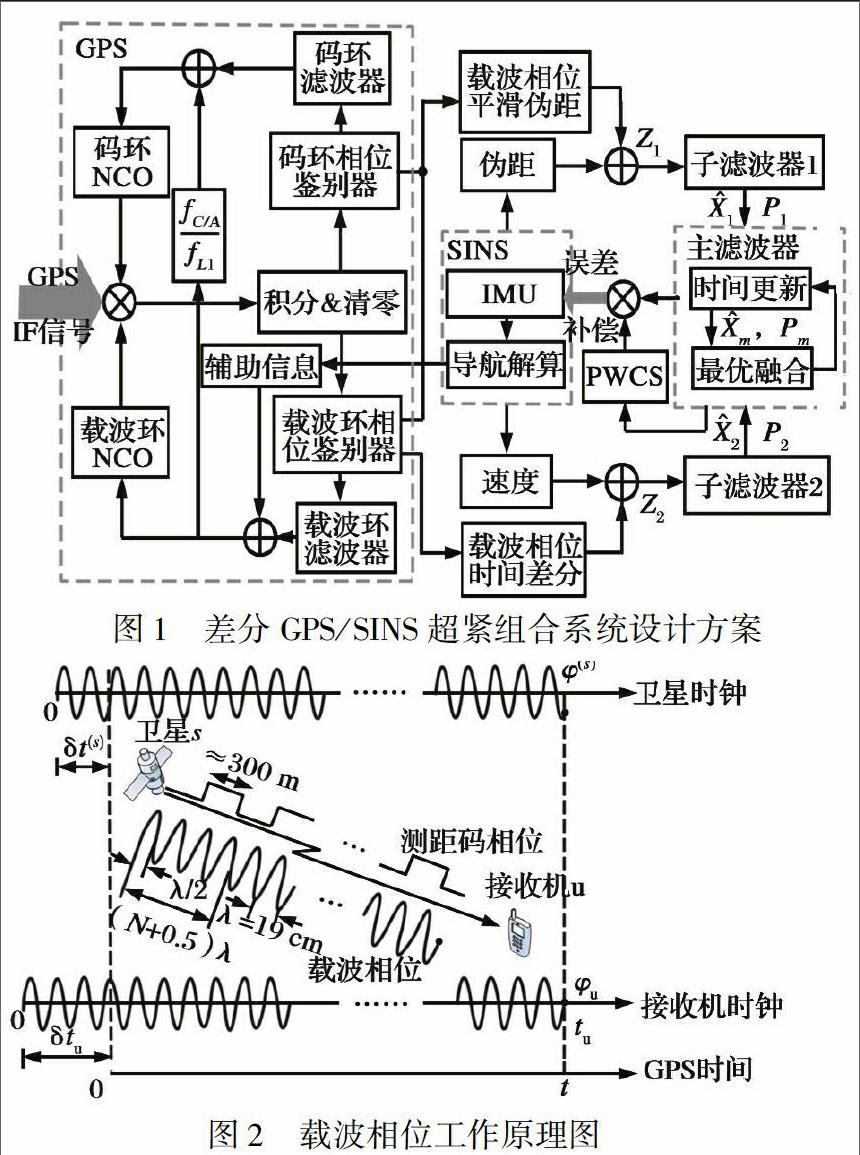
GPS/SINS组合导航系统通常采用Kalman滤波作为信息融合方式， 系统状态估计的精度与模型准确性和外观测量精度有关， 为提高GPS/SINS超紧组合导航系统的精度， 设计了一种采用载波相位差分高精度观测量的GPS/SINS超紧组合系统方案， 系统结构如图1所示。

超紧组合系统通过引入SINS对GPS跟踪环路的辅助， 减小了载波环的动态跟踪范围， 降低了载波环路噪声带宽， 跟踪环路内部采用载波环辅助码环的方法以消除码环的动态， 减小码相关间隔， 提高了载波环和码环的跟踪精度； 信号的高精度跟踪为载波相位作观测量提供了保证， 载波相位平滑伪距和载波相位时间差分速度作为组合导航滤波器的观测信息， 使得量测噪声减小， 进而提高组合导航精度。

高精度的载波相位时间差分速率和载波相位平滑伪距作为观测量， 可提高组合滤波器对SINS速度误差的估计效果， 而两者量测更新频率不同， 且噪声差异明显， 为避免在组合导航过程中， 载波相位时间差分速度的高精度被伪距的高噪声掩盖， 兼顾两者不同的信息更新速率， 将两部分观测量分离， 借鉴联邦滤波的思想进行组合导航， 以隔离两种观测量的量测噪声， 发挥外观测量的高精度优势。

2差分GPS/SINS超紧组合系统模型建立2.1载波相位观测模型的建立

航空兵器2016年第5期葛俊等： 差分GPS/SINS超紧组合在线标定与误差补偿方案设计伪距在过去一直被视为GPS接收机最主要的基本距离测量值， 然而现在载波相位越来越受到重视[2]， 两者既有明显区别， 又具有互补性。 载波相位的量测噪声远远低于测码伪距的量测噪声， 载波相位测量值平滑且精度高， 多路径效应对载波相位测量值的影响也远小于对伪距的影响。 但是限制载波相位应用于定位的关键问题是测量值含有整周模糊度。 整周模糊度解算的经典收敛时间在30 min左右[3]， 因此， 无法应用于实时导航。 然而， 连续跟踪的情况下， 整周模糊度保持不变， 可将相邻历元间载波相位作差， 消除整周模糊度， 并利用精确、 平滑的载波相位量测值来对无模糊度的伪距进行平滑。 载波相位工作原理如图2所示。

式中： j为参与导航解算的卫星编号； Hρ1为各导航卫星与载体之间的方向余弦转换至ECEF系的转换关系； Hρ2为GPS误差与观测量的关系。 3GPS/SINS在线标定及误差补偿方案的设计惯性导航系统的主要缺点是定位误差随时间累积而无法长时间准确提供导航信息[7]， 因此， 对惯导系统的误差标定及补偿技术是提高SINS精度的有效途径。 目前， 对惯导系统误差的标定多采用外部高精度的基准信息和惯导系统本身导航输出结果之间的差异， 结合载体某种机动动作达到误差激励的目的， 然后通过相应的估计方法将SINS和IMU的器件误差估计出来， 进而实现对SINS常值误差进行估计和补偿。

3.1最优误差估计方式

外部参考信息的不足会导致可观测性低， 在一定程度上可以利用合理的误差激励方式来弥补。 根据惯导系统的基本原理， 姿态误差激励在有重力加速度情况下即可实现， 航向误差可以根据水平方向加速度进行估计， 而惯性器件的常值误差项不需激励， 其对系统的影响也可以体现在导航误差中[8]。 因此， 目前提高误差估计精度的研究主要集中在： （1）设计合适的载体运动轨迹和自身的姿态变化来进行误差激励； （2）选取精度更高的外观测量来估计误差。

本文提出的方法采用较高精度的载波相位差分观测信息， 并结合了弹道导弹飞行特点， 在主动段利用导弹特定飞行轨迹进行标定， 利用导弹推力提供的加速度、 弹道导弹绕弹轴自转机动、 弹体俯仰角度的变化以及微小的水平机动来激励惯性元件的误差。

3.2GPS/SINS在线标定可观测度分析

由于系统状态变量的可观测度限定在[0，1]内， 可以作为滤波器状态估值的反馈因子， 当某个系统状态量的可观测度为1时， 表示该状态完全可观测； 当可观测度为0时， 表示该状态不可观测； 当可观测度在0～1之间时， 表示该状态变量可观测性差。 由此可以将估计误差与反馈因子相结合， 准确地反馈校正信息， 避免了错误的误差估计对组合系统导航性能产生影响。

4仿真验证与分析

为验证差分GPS/SINS超紧组合导航系统的导航性能及在线标定和误差补偿方法的有效性， 分别对载波相位差分GPS/SINS超紧组合系统的外观测量、 导航性能、 在线标定能力及误差补偿效果进行仿真与分析。

4.1高精度GPS外观测量模型仿真与分析

4.1.1载波相位平滑伪距误差仿真与分析

通过载波相位获得更加平滑、 准确的载波相位平滑伪距， 可以得到更精准的导航观测量。 GPS接收机获得的伪距和载波相位平滑伪距误差分别如图6～7所示。

由图6～7可以看出， 经伪距平滑后的伪距精度要高于普通伪距测量值， 这是由于码测量不能对卫星时钟和星历、 电离层和对流层引起的误差进行补偿， 而采用码测量与载波相位测量结合， 滤波器给予载波相位测量值相比于码测量更高的权重， 传播误差可以被补偿， 码测量的多径误差也可以在滤波器长度范围被平滑掉一些， 载波相位平滑伪距可以为组合导航系统提供更准确的观测量。

4.1.2载波相位时间差分速度误差仿真与分析

对GPS接收机载波相位时间差分方案进行仿真， 根据精密的载波相位测量信息， 可以计算出载体精密的速度信息。 GPS测得速度误差与载波相位时间差分方法解得载体速度误差的对比如图8～9所示。

由图8～9可以看出， 由于引入SINS对GPS跟踪环路的辅助， 减小了载波环的动态跟踪范围， 降低了载波环路噪声带宽， 提高了GPS信号跟踪环路的跟踪精度， 因此， 载波相位时间差分计算出的载体速度精度可以达到厘米级， 甚至毫米级， 相较于GPS解算速度， 精度提高了1～2个数量级。 这样就可以为组合导航滤波器提供精确的速度更新信息， 进而提高组合导航系统的精度。

4.2GPS/SINS在线标定结果仿真与分析

4.2.1仿真条件设置

具体的仿真条件为弹道导弹主动段飞行时间为100 s； 弹道导弹发射方位角为45°； 发射时刻俯仰角为90°； 初始速度为0 m/s； 导弹飞行过程中有俯仰和较小的偏航方向机动； 加速度计偏值稳定性为5×10-5g0（3σ）； 陀螺仪X， Y， Z轴零位漂移误差分别为0.03 （°）/h， 0.04 （°）/h， 0.05 （°）/h（3σ）。 借助推力实现弹道导弹标定飞行轨迹， 其轨迹如图10所示。

4.2.2仿真结果与分析

根据以上仿真条件， GPS/SINS在线标定的陀螺仪和加速度计常值误差项的结果如图11～12所示。

由图11～12可以看出， 在当前条件下， 惯性器件的常值误差项是可以标定的， 符合理论分析， 标定结果较为准确， 估计精度在允许范围内， 但是由于文中设计的机动形式不能够同等程度地激励IMU的所有误差， 因此， 估计的精度和收敛速度存在差异。 通过该仿真验证了在线标定算法的可行性， 惯性器件各常值误差均得到了较好的估计， 若增加载体机动动作， 对惯性器件各误差进行充分激励， 可以进一步提高标定精度。

4.3GPS/SINS误差补偿结果仿真与分析

根据上述在线标定结果， 将标定出的惯性器件的常值误差项反馈至SINS， 对其导航误差进行补偿， 在仿真条件完全相同的情况下， 对SINS误差补偿前后组合系统的导航性能进行仿真和分析， 结果如图13～15所示。

由图13～15可以看出， SINS经过在线标定的误差补偿后， 组合导航系统的各种误差均有所降低， 导航精度明显提升。 在线标定结果需要一段时间收敛到可用精度才可反馈至IMU， 根据反馈因子利用精度较高的在线标定误差对组合系统IMU进行补偿， 经组合导航滤波器信息融合后， 组合导航系统位置、 速度误差收敛更迅速， 误差波动范围更小， 相对于未补偿IMU误差的组合导航系统， 导航精度进一步提高。

5结论

设计了一种载波相位差分GPS/SINS超紧组合导航系统在线标定及误差补偿方案， 通过系统化方案设计和仿真验证分析， 得出以下结论：

（1） 引入SINS对GPS跟踪环路的辅助， 减小了载波环的动态跟踪范围， 降低了载波环路噪声带宽， 减小码相关间隔， 提高了载波环和码环的跟踪精度， 以保证输出高精度载波相位观测量。 相对于伪距和速度观测量， 载波相位观测量的精度提高1～2个数量级。

（2） 高精度外观测量和最优误差估计方式相结合的在线标定方案， 可准确标定IMU常值项误差， 根据反馈因子准确地反馈校正信息， 进一步提高组合导航系统的导航精度。

可见， 所提出的差分GPS/SINS超紧组合在线标定与误差补偿方案能够准确标定和补偿IMU常值误差， 进一步提高组合导航系统的导航精度， 具有广阔的工程应用前景。

参考文献：

[1] 王君帅， 王新龙. SINS/GPS 紧组合与松组合导航系统性能仿真分析[J]. 航空兵器， 2013（2）： 14-19.

[2] Hatch R， Sharpe R T， Yang Yunchun. An Innovative Algorithm for CarrierPhase Navigation[J]. Proceedings of ION GNSS， Long Beach， California， 2004.

[3] Bisnath S， Gao Y. Precise Point Positioning[J]. GPS World， 2009（20）： 43-50.

[4] GebreEgziabher D， Powell J D， Enge P. Design and Performance Analysis of a LowCost Aided Dead Reckoning Navigation System[J]. Gyroscopy and Navigation， 2001， 4（35）： 83-92.

[5] Van Graas F， Soloviev A. Precise Velocity Estimation Using a StandAlone GPS Receiver[J]. Navigation， 2004， 51（4）： 283-292.

[6] Wendel J， Meister O， Monikes R， et al. TimeDifferenced Carrier Phase Measurements for Tightly Coupled GPS/INS Integration[C]∥Proceedings of IEEE/ION PLANS， 2006： 54-60.

[7] 申亮亮， 王新龙， 陈涛. 舰载武器SINS速度+姿态匹配传递对准建模与仿真[J]. 鱼雷技术， 2008， 16（5）： 22-26.

[8] 陆志东， 王磊. 捷联惯导系统的空中标定方法[J]. 中国惯性技术学报， 2007， 15（2）： 136-138.

[9] Wang Q， Ding M， Zhao P. A New Scheme of NonGyro inertial Measurement Unit for Estimating Angular Velocity[C]∥Industrial Electronics Society， IECON03， 2003： 1564-1567.

[10] 钱伟行. 捷联惯导与组合导航系统高精度初始对准技术研究[D]. 南京： 南京航空航天大学， 2010.