基于IBIS－L系统的大体积混凝土温度形变场分析

吴琦，张戈，张硕，肖先煊

(1．华北水利水电大学，河南 郑州 450045;2．成都理工大学 地质灾害防治与环境保护国家重点实验室，四川 成都 610059)

大体积混凝土随着温度的变化会产生微量形变，由于其自身结构体系的复杂性和所处环境的多样性，必须充分考虑温度形变场对大体积混凝土产生形变的影响［1］．美国加州大学的E．L．Wilson［2］最早使用有限元时间过程分析方法计算了Dworkshak大坝的温度形变场． 韩国世宗大学的Jang-Ho Jay Kim 等［3］应用有限元法及差分法计算了坝体的温度形变场．在英国和法国，ADINA、ABAQUS、ANSYS 等有限元分析软件运用比较广泛［4］． 朱伯芳院士和宋敬廷合作编制了我国第一个混凝土温度形变有限元分析程序，把有限单元法运用于大体积混凝土结构温度形变场的计算分析中［5］．

为了进一步分析大体积混凝土桩板墙的微变与温度形变场之间的相关性，本文基于IBIS －L 地形微变远程监测系统，监测桩板墙随温度变化的实时形变量，利用有限元理论方法计算桩板墙产生的温度形变，并通过ANSYS 有限元软件进行仿真模拟，将温度形变场引入大体积混凝土的计算模型中，并结合实例总结两者之间的对应关系．

1 IBIS－L 系统变形监测分析

1．1 IBIS－L 系统简介

IBIS－L 地形微变远程监测系统是集合了步进频率连续波技术(SF － CW)、合成孔径雷达技术(SAR)和干涉测量技术的新型高级监测系统． 该系统通过合成孔径技术来获取监测区域的二维图像，并将监测区域划分为许多小单元，每个小单元都代表着一个监测点的变形，然后应用干涉技术提取其相位变化量［6］．该系统在人造卫星和陆地激光扫描的基础上对可靠性、精度予以改进，可应用于对建筑物和地形的静态监测． 其最大监测距离可达4 km，测量精度可达0．1 mm，最小图像采集时间为5 min，能够24 h 不间断地监测整个目标区域的位移变化量［7］．

1．2 IBIS－L 系统微变监测

研究区桩板墙在每日温度变化的影响下，整体产生微变位移．应用IBIS －L 系统对桩板墙的微变形量进行全方位连续监测，监测频率为1 次/h，周期为20 d．

为了减小监测时的误差，需要在整个监测区域范围内选取稳定的参照物作为地面稳定控制点(Ground Control Points，GCP)，也就是整个监测范围的基准点．本次监测在仪器位置前方的居民房屋附近选取2 个地面稳定控制点，并在桩板墙上由南向北选取8 个变形控制点进行定点分析． 监测时规定以IBIS－L 系统的安装位置为原点，仪器行进方向为x 轴，与之垂直的雷达波发射方向为y 轴，GCP点、变形控制点及其位移云图如图1 所示． 图中:正值表示背离仪器方向;负值表示靠近仪器方向．

根据IBIS－L 系统的监测结果，桩板墙20 d 内每日发生的微变与温度变化趋势几乎一致，其相对趋势曲线如图2 所示．

从图2 中可以看出:①8 个变形控制点的变化趋势相近，整体趋势一致;②桩板墙回弹变形的位移曲线和温度变化趋势几乎一致;③在温度形变场的影响下，监测到的变形回弹位移在4 mm 的范围内波动．

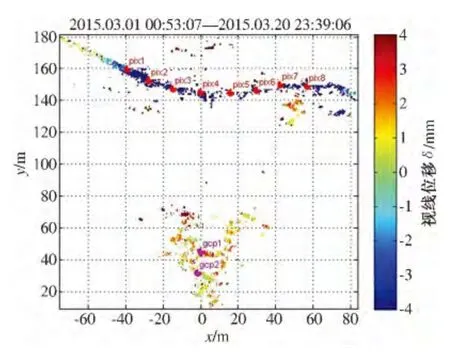
图1 GCP 点、变形控制点及其位移云图

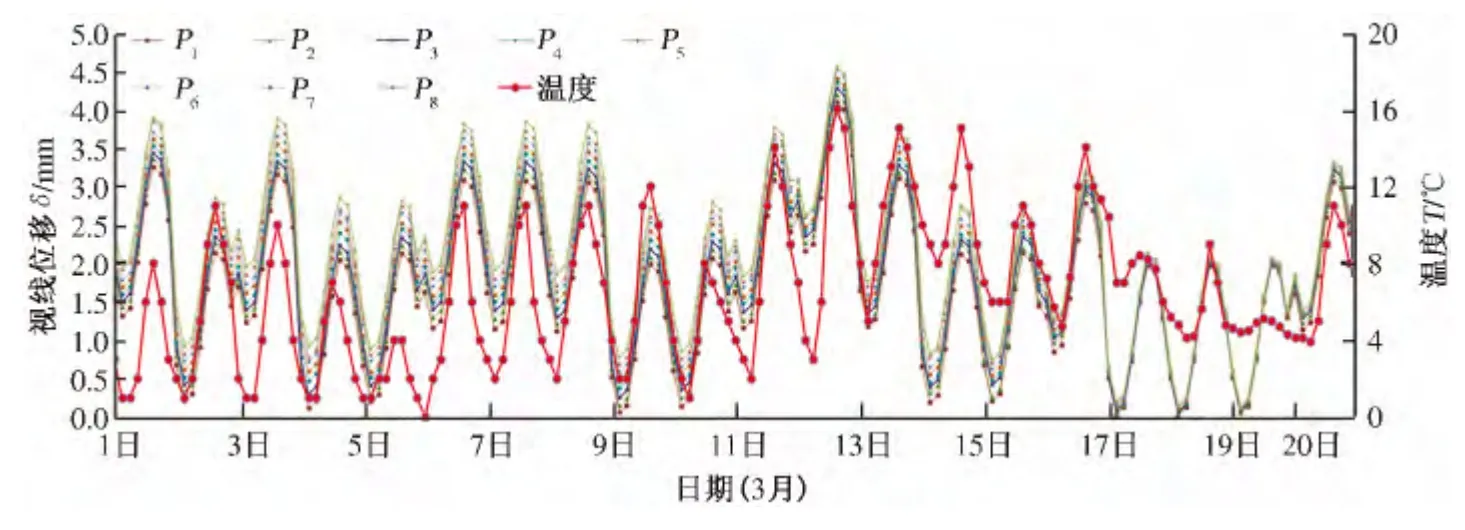
图2 桩板墙微变位移与温度变化趋势图

2 大体积混凝土桩板墙温度形变场的有限元计算

2．1 温度形变场热传导方程及第三类边界条件

假设混凝土为均匀的、各向同性的固体［8］，其热传导满足以下微分方程:

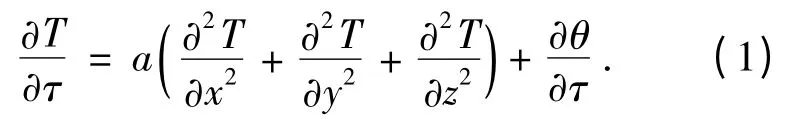
式中:T 为温度，℃;τ 为时间，h;a 为导温系数，m2/h;θ 为混凝土的绝热温升，℃．

第三类边界条件是大体积混凝土温度形变场计算最常用的边界条件． 混凝土与空气之间存在热交换［9］，经过混凝土表面的热流量q 为:

式中:λ 为导热系数，kJ/(m·h·℃);n 为边界外法线方向．

第三类边界条件假设经过混凝土表面的热流量q 与混凝土表面温度T 和气温Ta之差成正比，即

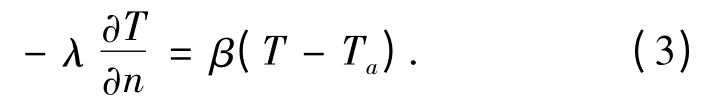
式中β 为表面放热系数，kJ/(m·h·℃)．

2．2 温度形变场的有限单元法计算

有限单元法是比较成熟的分析大体积混凝土温度场和形变场的数值计算方法，需要在空间区域内对结构体进行离散化，同时也必须在时间区域内进行离散化．当结构体的各部分温度发生变化时，结构体将由于热变形而产生线形变，为α(T－T0)．

大体积混凝土桩板墙由于不均匀温度场而产生线形变，未产生剪切形变［10］． 这种形变可以看作是结构的初形变ε0，由ε0可以求得等效节点温度荷载Pε0，然后按通常有限元方法求得节点径向位移δ．

对于三维单元e，有

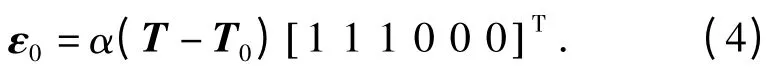
式中:α 为材料的热膨胀系数，1/℃;T0为结构的初始温度场，℃．

等效节点温度荷载Pε0的计算公式为:

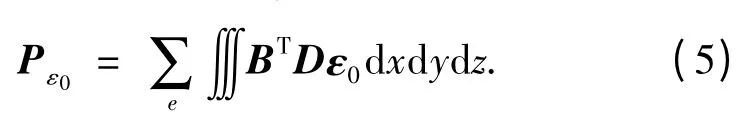
式中:B 为单元几何矩阵;D 为弹性矩阵;ε0为初应变矩阵．

根据虚位移原理，得出增量形式的等效节点温度荷载有限元方程，即

式中:K 为混凝土桩板墙的整体刚度矩阵;ΔPε0为温度增量引起的等效节点荷载．

研究场地桩板墙高20 m，桩体宽1．5 m，厚2 m，桩间板宽2 m．混凝土强度等级为C30，混凝土的热学参数见表1．

表1 混凝土的热学参数

由式(6)可求得桩板墙上8 个变形控制点由温度形变场引起的节点径向位移． 计算结果表明，8 个点的径向位移基本相同，与实测位移的变化趋势基本一致．以变形控制点P4为例，其在20 d 内的实测位移和径向位移变化趋势如图3 所示．由图3 可见，桩板墙随着温度的变化会产生不同的温度形变，由温度引起的径向位移的计算值的误差不超过2%．

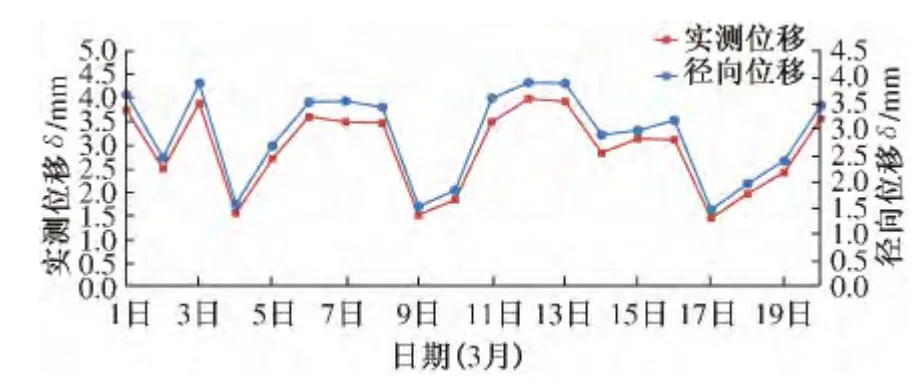
图3 桩板墙P4 点实测位移与径向位移变化趋势图

3 ANSYS 温度形变场模拟结果分析

桩板墙P4点第1 天和第20 天的温度分布云图如图4 所示，不同时期的温度形变如图5 所示．

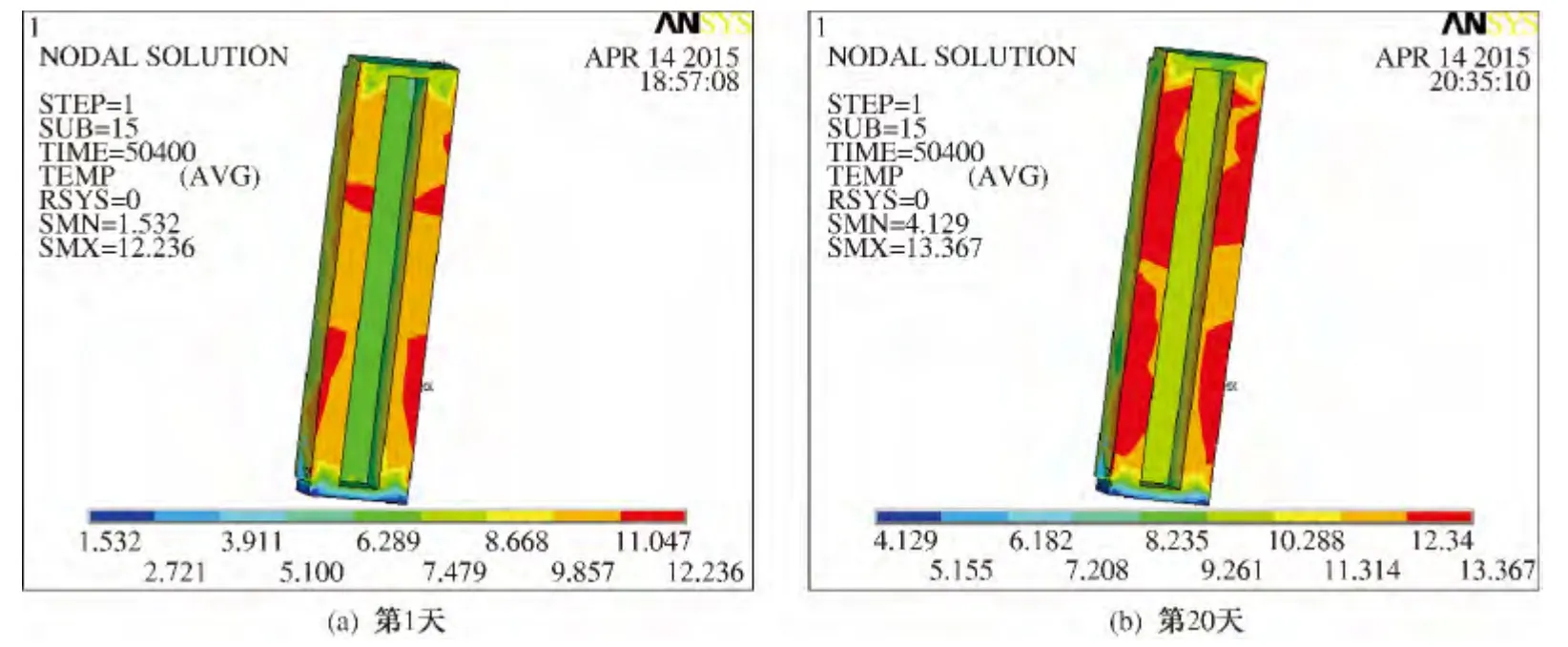
图4 桩板墙P4 点的温度分布云图

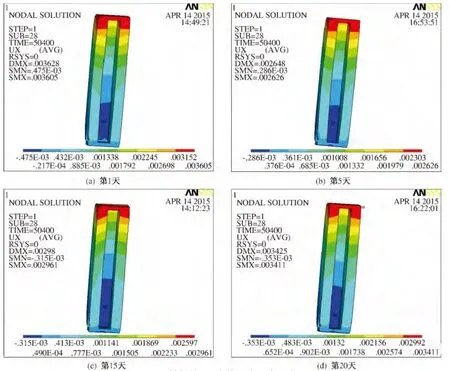
图5 桩板墙P4 点的温度形变分布图

从图5 中可以看出，桩板墙P4点在20 d 的监测周期内，当日温差变化较大时，其形变随之增大;反之则亦然．如第1 天温差为11 ℃，第20 天温差为9 ℃，二者随之产生的温度形变相差0．2 mm． ANSYS 有限元软件数值仿真模拟的温度形变在第1天、第5 天、第15 天、第20 天时分别为3．61、2．63、2．96、3．41 mm，这与IBIS －L 系统监测的实际数据基本相同．

4 结 语

1)IBIS－L 地形微变远程监测系统可以全方位精确地监测研究区桩板墙每天随温度变化而产生的微变位移，监测数据形成的微变位移曲线与实时温度变化曲线的变化趋势一致．

2)ANSYS 有限单元软件能够较好地仿真大体积混凝土桩板墙受温度形变场影响而产生温度形变的过程，其计算和模拟出来的温度形变与IBIS －L 系统实际监测的微变位移基本相同． 但是由于使用ANSYS 有限单元软件数值模拟桩板墙温度形变时对弹性模量、热力学公式等参数的选择过于理想化，导致数值分析的结果与现场实测数据之间存在一定的误差．

3)通过对现场20 d 的连续监测与分析，8 个变形控制点对应的大体积混凝土桩板墙的温度形变有如下规律:连续高温或连续低温时，其产生的变形变化量较小，曲线走势较平稳;连续高低温交错，即相对温差较大时，产生的变形变化量较大，曲线走势会出现突增现象．

［1］朱伯芳． 大体积混凝土温度应力与温度控制［M］． 北京:中国电力出版社，1999:1 －3．

［2］Malkawl Abdallah I Husein，Mutasher Saad A，Qiu Tony J．Thermal-structural modeling and temperature control of roller compacted the concrete gravity dam［J］． Journal of Performance of Constructed Facilities，2003，17(4):177－187．

［3］Jang-Ho Jay Kim，Sang-Eun Jeon，Jin-Keun Kim． Development of new device for measuring thermal stresses［J］．Cement and Concrete Researsh，2002，32(10):1645－1651．

［4］张朝晖．ANSYS12．0 热分析工程应用［M］． 北京:中国铁道出版社，2010:1 －101．

［5］胡少伟，鲁文妍．基于XFEM 的混凝土三点弯曲梁开裂数值模拟研究［J］． 华北水利水电大学学报(自然科学版)，2014，35(4):48 －51．

［6］邱志伟，汪学琴．地基雷达系统IBIS－L 在大坝变形监测中的应用［J］．长江科学院院报，2014，31(10):104－107．

［7］王峰，许强，肖先煊，等．基于地形微变远程监测系统的滑坡变形监测［J］．长春工程学院学报(自然科学版)，2014，15(1):66 －71．

［8］康明睿，薛伟辰．配FRP 箍筋混凝土梁的抗剪性能研究进展［J］．华北水利水电大学学报(自然科学版)，2015，36(2):15 －20．

［9］刘亚基，苏志敏．大体积混凝土浇筑块温度应力场直接耦合法仿真计算［J］． 科学技术与工程，2010，10(16):57 －60．

［10］黄君宝． 大体积混凝土温度场应力场仿真方法研究［D］．天津:天津大学，2009:21 －22．