基于最大熵原理的洪水灾害灾情评估改进普适模型

唐言明，卜松，董洪茂，范江洋

(1．中海油山东化学工程有限责任公司，山东 济南 250101;2．安徽新华学院 土木与环境工程学院，安徽 合肥 230088)

灾情综合评价工作是制定防灾救灾规划和具体安排防灾救灾措施的基础，可为政府部门合理安排筹措救灾资金、布局灾区恢复重建，以及为保险部门的灾后赔偿和政府资金的分配提供强有力的依据［1］．它是通过计算研究地区在某时间范围内可能发生的一系列不同强度的灾害给该地区造成的可能损失，估计其损失的概率分布，并依据研究地区所得到的灾情指标集，应用建立在一定的灾情指标体系下的灾害灾情综合评估模型，对该地区灾情进行综合评价．目前常用的方法是物元分析评价模型、模糊综合评价模型及基于神经网络的智能模型等［2－5］．沈瑜等［6］利用指数普适公式进行洪灾评估，并利用遗传算法优化公式参数，最终得到洪灾灾情评价普适指数公式．上述模型均是从样本数据集本身进行灾害等级评估，但由于灾害的发生具有复杂的时空统计特性，估算其发生的概率分布是一个难点，且这些模型均是从指标权重方面或按照均权考虑的，这种概率分布可用最大信息熵原理解决［7－8］． 在设定各损失指标基准损失值、损失评价模型中采用损失的相对值情况下，可利用最大熵原理计算概率分布，并利用加速遗传算法(Accelerating Genetic Algorithm，AGA)对参数a、b 及分布概率Pij进行优化，得到合理的灾情指数普适计算公式． 本文提出了用信息熵来处理指标数值的分布概率，用加速遗传算法优化相关参数［9］，进而建立了基于信息熵的AGA 优化灾情评估普适新模型，并进行了实例应用研究．

1 基于信息熵的改进普适评估模型的建立

步骤1 灾害损失样本集的无量纲化处理． 若分别对每个指标设定一个参照基准值sj0，用uij表示指标值xij相对于基准值sj0的符合程度，这样消除了指标的量纲效应，使其具有通用性，即无量纲化． 由于uij的取值变化范围较大，常用其对数作为评估样本指标值，

步骤2 计算各样本的指数普适值Iij． 在灾情评价中，从微灾到轻灾，其评价指标数值变化很小，受灾程度变化轻微，且差异度小，因此用来表示损失程度的函数变化曲线应该平缓;在重灾到巨灾范围，虽然评估指标数值变化大，但就受损程度而言，区别不明显，因此评估指数函数变化也应趋于平缓;在轻灾到重灾之间时，其变化范围虽然不大，但是其损失程度变化范围却很大，故其评估指数变化范围应该较大．反映评估指数的函数应该符合“缓慢— 快速—缓慢”规律，所以采用S 型曲线指数公式进行评估［6］．其灾情评估普适公式可表示为［6－7］:

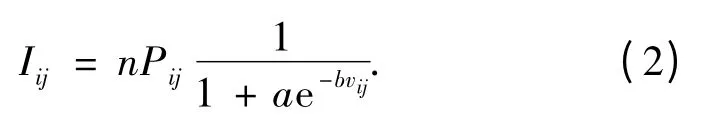
式中:Iij为灾情评估指数值;a、b 为待优化变量;n 为指标数目;Pij为第i 个样本与第j 个等级的符合度．

为构造合适的S 型曲线指数公式，需要构造目标函数

式中:Iij由式(2)计算得到;I0j为各个指标损失的目标值．各个损失指标值的基准值是各个等级的第1 级．

步骤3 计算灾害发生的概率分布． 由于灾害发生具有不确定性，故Pij的确定具有一定的模糊性和随机性．引入广义的加权距离之和描述样本与等级的符合度． Pij具有不确定性，其可以理解为相当于样本i 属于第j 个等级的概率，这样的不确定性可用信息熵表示，由此可引入最大熵原理［8］，且满足．在掌握部分信息后依据最大熵原理做出的分布是最合理的，也是唯一正确的选择，表示如下:

步骤4 确定目标函数． 为有效计算样本与等级之间的符合度，综合式(3)、(4)，可构造如下形式的目标优化函数:

上述优化问题是一个以a、b 及Pij(i =1，2…，n;j=1，2…，m}为变量的多目标非线性优化函数．常规优化方法处理上述问题较困难，而模拟生物优胜劣汰规则与群体染色体信息交换机制的加速遗传算法(AGA)是一种通用的全局优化方法，用它解上述问题较为简便［9］．

步骤5 进行区域灾情评价． 将指标的评价等级门限值sjk转换成相应的灾害指数值．把优化结果代入下式计算k 级等级相应的灾害指数值Ik(评价等级的指数值和样本数据的指数值转换是一致的)，其表达式为:

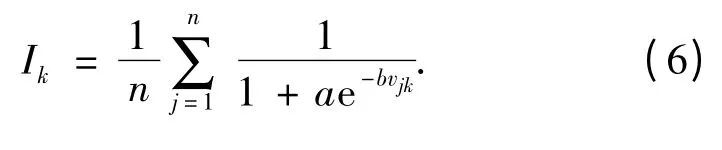
最后利用上述结果与Ik比较，进行等级判别．

2 应用实例

选取的实例来源于文献［10］，对1990 年湖南、上海、广东、福建等区域的灾害数据样本进行计算，进一步说明基于信息熵的改进灾情评估普适模型的应用过程．上海、湖南和浙江处于长江中下游，属于长江沿线的地区，受暴雨的影响，长江易发生洪水进而使该地区发生洪水灾害;广东、福建和浙江处于台风易发的南方沿海地区，受台风影响易造成灾害损失;其他地区属于北方地区，受台风及暴雨的影响较小;自改革开放以来，这些地区的经济飞速发展，自然灾害也给这些地区造成了严重的经济损失，研究这些地区的灾害情况，进行灾情综合评价工作对救灾防灾工作具有重要意义．根据文献［10］选取的样本数据见表1，其各级标准值选用参见文献［6］的标准，见表2．

表1 自然灾害各级标准值和参照基准值

表2 1990 年我国部分省市的自然灾害损失各项指标情况表

将上述数据以及结果见表3．根据式(7)计算灾情评估综合指数，最后判别灾害等级．为便于比较分析，表4 列出了文献［6］中其他方法的评价结果．

表3 灾害等级与灾情评估指数的对应关系

表4 样本的指数值和灾情评估结果

由表3—4 可知，基于信息熵的改进灾情评估普适模型对上述区域的灾情评估结果是合理的，该评价结果和文献［6］中基于GA 优化的灾情评估普适公式的评估结果和非关联度法的评估结果基本一致．湖南、上海等地区的自然灾害损失处于2 ～4 级，南方的灾害损失尤为严重(这与南方的气候和地理环境有关)，因此需要政府部门进一步制定和发展防灾救灾措施，做好防灾救灾规划，尽量降低自然灾害所造成的损失．灾害评估结果说明该模型有效合理地做出了灾害发生的分布概率，比文献［6］中基于GA 优化的灾情评估普适公式的评价结果更为合理，准确度更高．

3 结 语

针对灾害灾情评价过程中的不确定性以及指标的随机性和等级的模糊性，提出了基于最大熵原理的指数普适公式;为了反映灾害损失随等级的变化符合“缓慢—快速—缓慢”的变化规律，用S 型函数来计算损失的函数值;为弥补目标优化函数变量过多、易出错的不足，用模拟生物优胜劣汰规则与群体信息交换机制的加速遗传算法(Accelerating Genetic Algorithm，AGA)优化目标函数，进而建立了基于信息熵的改进AGA 优化灾情评估普适模型．该模型在区域灾害评价中的应用结果说明:用该模型进行灾情评价，物理概念清晰，精度较高，结果合理、有效，在各种灾害灾情评价中具有推广应用价值．

［1］魏一鸣，金菊良，杨存建，等． 洪水灾害风险管理理论［M］．北京:科学出版社，2002:1 －15．

［2］金菊良，丁晶．水资源系统工程［M］．成都:四川科学技术出版社，2002:161 －203．

［3］魏一鸣，万庆，周成虎． 基于神经网络的自然灾害灾情评估模型研究［J］．自然灾害学报，1997，6(2):3 －8．

［4］李祚泳，邓新民．自然灾害的物元分析灾情评估模型初探［J］．自然灾害学报，1994，3(2):28 －33．

［5］赵黎明，王康，邱佩华．灾害综合评估研究［J］． 系统工程理论与实践，1997(3):64 －70，83．

［6］沈瑜，徐婷婷，李祚泳．基于GA 优化的灾情评估普适公式［J］． 成都信息工程学院学报，2004，19(3):388－391．

［7］李祚泳，邓新民，张欣莉，等． 基于GA 优化的水质评价的污染损害指数公式［J］．环境保护，2001(3):24 －26．

［8］金菊良，洪天求，王文圣．基于熵和FAHP 的水资源可持续利用模糊综合评价模型［J］．水力发电学报，2007，26(4):22 －28．

［9］金菊良，魏一鸣． 复杂系统广义智能评价方法与应用［M］．北京:科学出版社，2008:205 －226．

［10］赵阿兴，马宗晋． 自然灾害损失评估指标体系的研究［J］．自然灾害学报，1993，2(3):1 －7．