基于模糊灰元的鄂尔多斯市水资源配置方案评价
张宇,彭少明,陈南祥
(1.华北水利水电大学,河南 郑州 450045;2.黄河勘测规划设计有限公司,河南 郑州 450003)
水资源作为一种基础性资源,对一个国家的综合发展起着不可或缺的作用. 随着社会经济的飞速发展,有限的水资源供给量与持续增长的水资源需求量间的矛盾不断激化[1].加之近年来由于人类活动引起的各种水体污染问题倍增,水资源浪费现象加剧,能够被人类有效利用的水资源量逐渐减少,更严重阻碍了社会经济的发展.为此,相关学者从配置方法上相继展开研究,希望通过更好的手段获取更加准确的配水方案,以缓解水资源短缺给区域发展带来的压力.但是,水资源的优化配置属于多目标优化问题,配置过程中涉及因素众多.根据研究人员对模型选择的不同,其配水结果间呈现较大差异. 另外,在实际运用中经常出现配水方案与实际需求不相符的现象,导致其达不到预期的经济效果,决策者不愿实施.为改变现有的局面,使得配水方案更好地被决策者接受,实现高效、经济用水,在方案实施之前就需要对其进行评价、验证.
目前水资源配置方案效果评价方法主要有专家会议法、主成分分析法、集对分析法、模糊综合评价法、灰色关联分析法、人工神经网络法等[2-6]. 经过长期研究发现,各种方法都存在一定的不足,例如:主成分分析法在对高维变量处理时容易遗失信息,造成评价结果出现较大偏差;模糊综合评价法在确定隶属函数时通常带有较强的主观任意性;灰色关联分析法对简单模型较为适用,对于复杂模型则表现欠佳.模糊灰元是集物元分析、灰色系统理论、模糊数学三大理论为一体而发展起来的一种理论,也是对水资源配置方案进行评价的一种新的方法[7].
1 评价方法
1.1 物元分析
物元分析是我国蔡文教授[8]于1983 年提出的,主要用于解决多因子评价过程中常常出现的不相容问题,通过建立由事物名称M,事物特征C,以及关于特征向量值V 所组成的三元有序组R(M,C,V)(称之为物元)这一全新概念,化解不相容为相容.建立“可拓决策”法,在保证以最大程度满足主系统、主条件的前提下,通过物元变换理论求解实际生活中存在的大量不相容问题.
1.2 灰色系统
灰色系统理论是我国邓聚龙教授[9]于1982 年提出的关于信息的不完整性或不确定性的系统控制理论,通过对已知信息的筛选,进一步对系统进行正确的描述.人们广泛接受控制论中的以颜色深浅来表达对信息的明确程度,例如将未知信息表示为黑,已知信息描述为白,故而“灰色系统”即为部分信息明确、部分信息不明确的系统[10]. 灰色系统理论的重点在于对信息的处理利用,通过不断地补充信息使系统白化.灰色系统中常常涉及灰数、灰元、灰色关系等相关特征.近年来,各领域研究人员广泛运用灰色关联法进行方案评价.
1.3 模糊数学
模糊数学相关理论最早是由美国的控制论专家Zadeh 教授[11]提出的.该理论以隶属函数作为桥梁量化问题的模糊性,从而将不确定问题转化为确定性问题,之后可运用传统数学方法对其进一步求解.整个过程的核心问题则转化为隶属函数的建立问题.模糊数学相关理论为研究现实生活中许多界限不分明的、甚至是很模糊的一系列问题提供了一种方法,在模式识别、人工智能等方面有广泛的应用.
2 模糊灰元模型
结合物元分析中的三元有序组的思想,如果其3要素的量值既有模糊性又有灰色性,则此时事物M、特征C、量值V 形成了模糊灰元.因此给出如下定义:由事物M、特征C、模糊灰量值V 组成的一个有序三元组来描述事物的基础元称之为模糊灰元,记作其中表示相应事物特征的模糊灰量值.则由m 个事物n 个特征构成的模糊灰元可表示为:

在模糊灰元分析的基础上将配水方案的评价等级划分为物元,将指标值对评价等级的隶属函数加以改进,可得到相应的模糊灰元矩阵.
2.1 模糊灰元评价过程
2.1.1 构造白化模糊灰元模型
当物元中的模糊灰量值被白化,得到量值为白化的模糊灰量值时,由事物、特征、白化模糊灰量值构成的三元组可记为. 按式(1)建立模糊灰元模型.
2.1.2 关联变换与关联度通常以关联函数ξ(x)来表示两事物之间的关联性.在模糊灰元模型中,由于关联函数ξ(x)与隶属函数μ(x)中含相同元素x,并且此时其区别仅仅在于前后二者的量值范围. 若此时将经典域与节域范围重合,则二者可以看作相互等价.
关联函数中如果xji已知,则可根据相应关系求解具体的函数值.在此称其为关联系数,记作ξji.其取值可根据关联函数与隶属函数的等价关系求出.
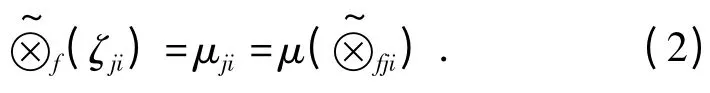
式中:j=1,2,…,m;i=1,2,…,n.
2.1.3 从优隶属度原则
在构造评价指标关联度系数白化模糊灰元时,为使结果便于后期比较可按下式进行转换.
越大越优型

越小越优型
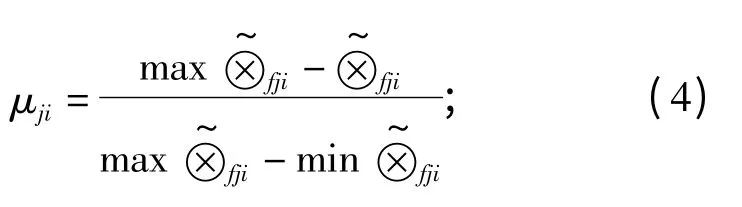

2.1.4 关联系数白化模糊灰元模型
根据从优隶属度原则中的计算公式得到方案的白化模糊灰量值关联系数值,建立复合模糊灰元为:

通过对关联系数量化的各事物与新的模糊灰元模型的事物进行灰色关联分析,关联系数量化的各事物与新的模糊灰元模型的事物关联度越大,则越优.
2.1.5 权重确定
权重的确定方法很多,常用的有德尔菲法、熵值法以及求和归一法等,权重的确定对于评价结果具有很大影响,本次研究采用二元比较模糊量化法,根据选取的n 个特征对于设定的m 个级别的权值,运用排序一致性定理,可以得到n 个指标特征重要性排序一致性标度矩阵,之后再通过专家对给出的n个指标两两比较,做出关于重要性程度的二元比较判断,利用语气算子与其相对隶属度间关系求得各个评价指标的权向量P,经过归一化得到最终权向量.
2.1.6 关联度计算及结果分析
根据评价指标关联度系数白化模糊灰元与指标权重按下式计算关联度:
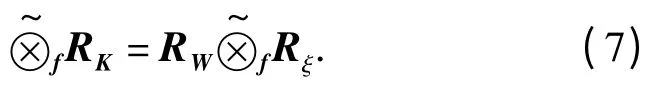
根据计算结果按照关联度大小进行排序,关联度越大越优.
3 实例应用
鄂尔多斯市位于黄河上中游属于干旱、半干旱地区,是我国西北主要的能源工业化城市,在国家能源战略中有着十分重要的地位.近年来,结合我国西部大开发战略提出的“以煤炭为主体、电力为中心,油、气和新能源全面发展[13]”的能源中长期发展规划和煤化工时代的来临,鄂尔多斯市迎来了其经济加速发展的黄金时期. 目前国家也在积极推进“呼包鄂”一体化的步伐.由此可见,在未来一段时间内鄂尔多斯市经济形势必会继续保持较快的速度发展.鄂尔多斯市特殊的地理位置使其表现出降水量少、蒸发强度大的特点,相关统计表明该地区蒸发强度是降水量的9 倍多.该市80%以上的水资源消耗在农业上,而该地区农业生产总值占该地区生产总值不到3%.农业用水挤占工业用水现象严重,与其目前定位不符.有关预测[14]表明,2020 年鄂尔多斯市总需水量将达到25.04 亿m3,届时该地区水资源可利用量只有21.85 亿m3,水资源缺口仍超3.00 亿m3.迫于现状事实压力,未来几年内鄂尔多斯市急需开展相应的水源工程和供水网络的建设,联合实施农业水源置换,进一步形成以本地水、外调水、非常规水源和应急备用水源等形成的多水源联合的供水保障格局.
为缓解当前严峻的供水形势,当地政府已采取多种工程、非工程手段来优化现状供水格局.就目前来讲,水资源合理配置是缓解水资源短缺问题的行之有效的方法,但由于水资源配置过程中涉及的因素众多,导致其配置结果并不能直接投入实际运用.为了向决策者提供一定的决策依据,使所选方案能顺利实施,通常需要验证所选方案的优劣性并对获得的方案进行评价验证. 现阶段关于配置效果评价方面已形成相当多的研究方法,笔者选用模糊灰元方法进行水资源配置方案评价,希望能够为水资源决策层提供相关建议与支持.
根据鄂尔多斯市发展规划对2020 年各部门需水进行的预测,按照现状供水规律进行水资源优化配置,其结果见表1,以此为样本方案展开评价.
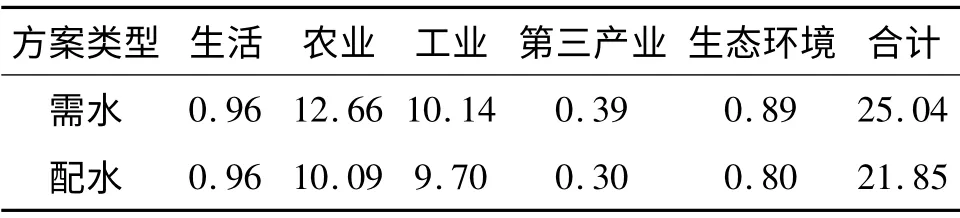
表1 2020 年鄂尔多斯市需水及配水方案亿m3
3.1 水资源配置方案评价指标体系的建立
针对鄂尔多斯市现状年的具体情况,在此次进行水资源配置评价时综合选取生活、农业、工业、第三产业、生态5 个方面进行水量分配,并以此建立相对应的评价指标特征体系. 将评价等级很好、略好、略差、很差作为物元的事物,分别记为M1、M2、M3、M4.以选取的生活、农业、工业、第三产业、生态5 个指标作为事物特征,记为C1、C2、C3、C4、C5. 相应指标分级标准见表2.

表2 5 项指标的分级标准
3.2 构造白化模糊灰元模型
根据表2 建立的5 项指标的分级标准构建相应的白化模糊灰元模型为:

3.3 评价指标关联度系数的白化模糊灰元模型

3.4 确定指标权重
权重的确定对于评价结果具有很大的影响,本次研究采用二元比较模糊量化法,得到鄂尔多斯市水资源配置方案中选取的5 个指标特征的权重向量
P=(1.00,0.33,0.78,0.56,0.11).
对其进行归一化处理,得到最终的权重向量
RW=(0.36,0.12,0.28,0.20,0.04).
3.5 关联度计算及结果分析
按式(7)计算所选方案对各级别的关联度
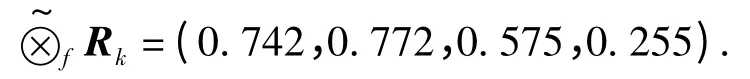
按计算所得关联度大小进行排序M2>M1>M3>M4.由此可看出,该配水方案属M2略好. 表明所选配水方案基本能够满足2020 年鄂尔多斯市的各部门水量需求.
考虑到该地区今后将面临的重要转型,工业用水会急剧增加,生活用水亦会出现平稳上升,生态需水的比重也将进一步加大,仅通过优化手段并不能从根本上解决水资源短缺问题.因此,今后仍需寻求其他工程、非工程措施来降低水资源需求总量,通过优化产业布局、降低用水定额、开展非常规水源的利用,进一步缓解供水紧张的局面.
为了验证模型的适用性,采用文献[15]中的模糊识别方法进行计算. 以文献中所建立的模糊模型进行验证:

式中:H 为级别特征值;h 为级别;uhj为样本j 对级别h 的相对隶属度.
本次研究中所选方案对于各个级别的相对隶属度为:
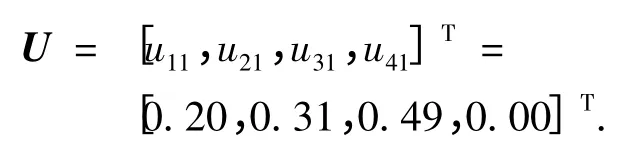
得到的计算结果为:

即该方案为三级评价等级,水资源配置方案略好.2种方法计算所得结果一致,表明所建立的模糊灰元模型对水资源配置方案评价具有很好的适用性.
4 结 语
本文将结合模糊数学、灰色系统及物元分析三大理论建立的模糊灰元模型运用到鄂尔多斯市水资源配置方案评价中,并与模糊识别评价模型结果进行对比,发现2 种方法所得评价结果一致,均得出所选方案略好、基本能够满足规划年鄂尔多斯市各方面的需水要求的结论. 表明模糊灰元法评价结果可靠,能够在水资源配置效果评价方面得到很好的运用.
[1]刘文祥.水资源危机[M].贵阳:贵州科技出版社,2001:9 -10.
[2]袁万海. 基于主成分分析的多元集成综合评价模型[J].技术与创新管理,2011,32(4):378 -382.
[3]高军省,崔凯.水资源开发利用程度综合评价的集对分析法[J].人民黄河,2010,32(12):94 -96.
[4]王文川,徐冬梅,邱林,等.基于可变模糊集理论的节水灌溉方式优选[J].节水灌溉,2011(9):30 -32,35.
[5]于洪涛,吴泽宁.灰色关联分析在南水北调中线澧河水质评价中的应用[J].节水灌溉,2010(3):39 -41,45.
[6]张先起,刘慧卿,梁川. 云南水资源可持续利用程度评价的自组织神经网络模型[J]. 长江流域资源与环境,2007,4(4):456 -460.
[7]张鹏,段永红,彭星煜. 基于模糊灰元理论和模糊层次分析的油气管道有限费用最优维护决策分析[J].中国科技论文在线,2010,11(11):861 -867.
[8]杨阳,方国华,黄显峰,等.基于改进模糊物元分析法的区域最严格水资源管理评价[J].水资源保护,2014,30(6):19 -24.
[9]刘思峰,党耀国,方志耕,等. 灰色系统理论及其应用[M].开封:河南大学出版社,1991:1 -5.
[10]刘维学.系统评价指标体系与灰色模糊评价模型构建[J].计算机技术与发展,2013,23(10):193 - 196,200.
[11]谢季坚,刘承平. 模糊数学方法及其应用[M]. 武汉:华中科技大学出版社,2000:2 -3.
[12]罗景峰,许开立. 安全投资决策的可变模糊优选方法[J].中国安全生产科学技术,2010,6(5):87 -91.
[13]贺丽媛,苏柳,贾冬梅,等. 鄂尔多斯市水资源需求预测研究[J].人民黄河,2014,36(9):59 -61.
[14]彭少明,贺丽媛,崔长勇,等. 鄂尔多斯市水资源供需分析与配置格局[J].人民黄河,2014,36(9):62 -63,79.
[15]陈文艳,王好芳. 基于模糊识别的流域水资源配置评价[J].水电能源科学,2009,27(4):29 -30,66.

