基于虚加刚性弹簧法的守口堡坝的有限元分析
田青青,杨世锋,柴启辉,孙明权
(华北水利水电大学,河南 郑州 450045)
胶凝砂砾石材料是一种新的坝体填筑材料,它是直接在河床砂砾料中掺入少许的胶凝材料(主要是水泥、粉煤灰)搅拌而成,较常态混凝土与碾压混凝土而言具有造价低、施工工艺简单并且温度控制要求低等优点.对胶凝砂砾石坝进行强度、刚度及稳定性方面的安全校核,首要任务就是对坝体进行应力与变形分析.笔者在前期胶凝砂砾石坝本构模型研究[1-2]和非线性分析[3]的基础上,结合山西守口堡坝实际工程对胶凝砂砾石坝的应力与变形特性进行了进一步的探讨.
1 工程概况
守口堡坝位于山西省黑水河上游,是我国首座永久性胶凝砂砾石坝. 该坝最大坝高为61.6 m,坝顶宽6.0 m,上下游边坡比均为1∶0.6,胶凝材料的配合比为50 kg/m3的水泥和40 kg/m3的粉煤灰,砂率为0.418,水胶比为1.58.以守口堡坝胶凝材料的配合比为基准制备试样,进行三轴剪切试验,得出试样在不同围压下的28 d 龄期的应力-应变曲线,如图1 所示.
由图1 可知,胶凝砂砾石材料的特性如下:①胶凝砂砾石材料是一种弹塑性材料[4],具有明显的弹性区和塑性区;②同一配合比下,围压越大,偏应力(σ1-σ3)峰值强度越高,峰值应变越滞后,对应的残余强度也越高;③当应变ε 在2%左右时,偏应力(σ1-σ3)达到峰值;当应变ε 为2% ~6%时,曲线下降趋势明显,体现出明显的软化特性[5];当应变ε超过6%以后,曲线的下降趋势逐渐趋于平缓,最后趋于残余强度.
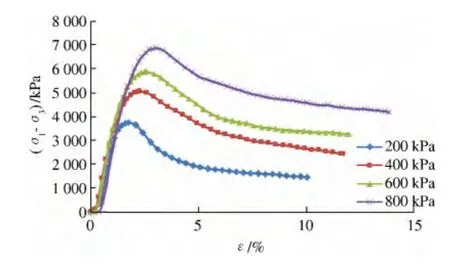
图1 守口堡坝28 d 龄期的应力-应变曲线
2 本构模型的建立及模型参数的确定
目前在土体的应力-应变分析中,工程中广泛采用的是邓肯-张双曲线模型.该模型理论成熟,应用简单,实践经验较丰富. 由三轴试验结果可知,只要解决胶凝砂砾石材料的应力-应变曲线的软化问题,其本构关系就可用双曲线模型来描述.
2.1 邓肯-张双曲线模型简介
1)该双曲线模型的切线变形模量Et的计算式为:[6]

式中:c,φ 分别为土体的黏聚力和内摩擦角;P0为大气压;k,n 分别为关系直线的截距和斜率,n 为无因次基数(试验参数);Rf为破坏比.
2)切线泊松比vt的计算式为
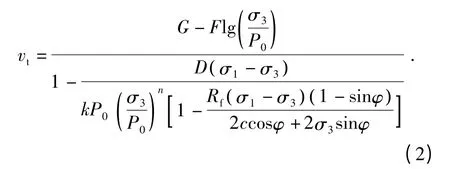
公式(2)中引入了G、F、D 3 个参数,加上切线变形模量的5 个参数,共8 个参数.
2.2 胶凝砂砾石材料本构模型的建立
由胶凝砂砾石材料的应力-应变特性可知,偏应力在达到峰值后存在软化阶段.在这一阶段,偏应力(σ1-σ3)随着轴向应变ε 的增加而降低,此时确定的切线弹性模量是负值,故双曲线模型不能直接使用,应采用虚加刚性弹簧法[7]处理后再使用.
2.2.1 虚加弹簧法的基本原理
虚加弹簧法的基本原理是在曲线的适当位置加上虚拟的弹簧,如图2(b)所示. 采用虚加刚性弹簧法以后,实际胶凝砂砾石材料的切线模量如图2(a)中的曲线①,是由虚加弹簧后的切线模量E'(图2(a)中的曲线③)减去虚加刚性弹簧的弹性模量(图2(a)中的曲线②)后所得到的,即:

式中:Et为实际胶凝砂砾石材料的切线模量;E'为虚拟模型的切线模量;ED为虚加刚性弹簧的弹性模量,本文取实际应力-应变曲线的1 倍和2 倍最大负弹性模量的绝对值,分别为126 MPa 和252 MPa.
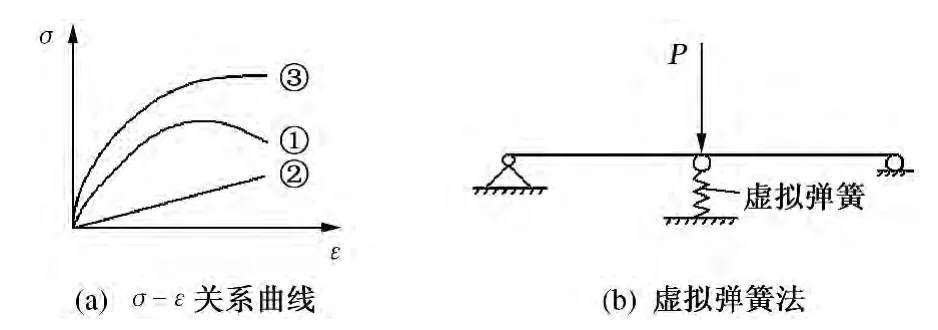
图2 虚加刚性弹簧法示意图
2.2.2 虚加弹簧法的应用
在图1 所示的应力-应变曲线上叠加一条如图2(a)所示的应力-应变直线②,得到如图3 所示的新应力-应变曲线.
从图3 可以看出,偏应力(σ1-σ3)随着轴向应变ε 的增大而增大,偏应力峰值及应变软化阶段都不存在,曲线可近似看作双曲线. 在同一配合比下,胶凝砂砾石材料的偏应力值随着围压的增大而增大,且在应变大于6%以后,呈现一组基本平行的、接近于直线的曲线组.
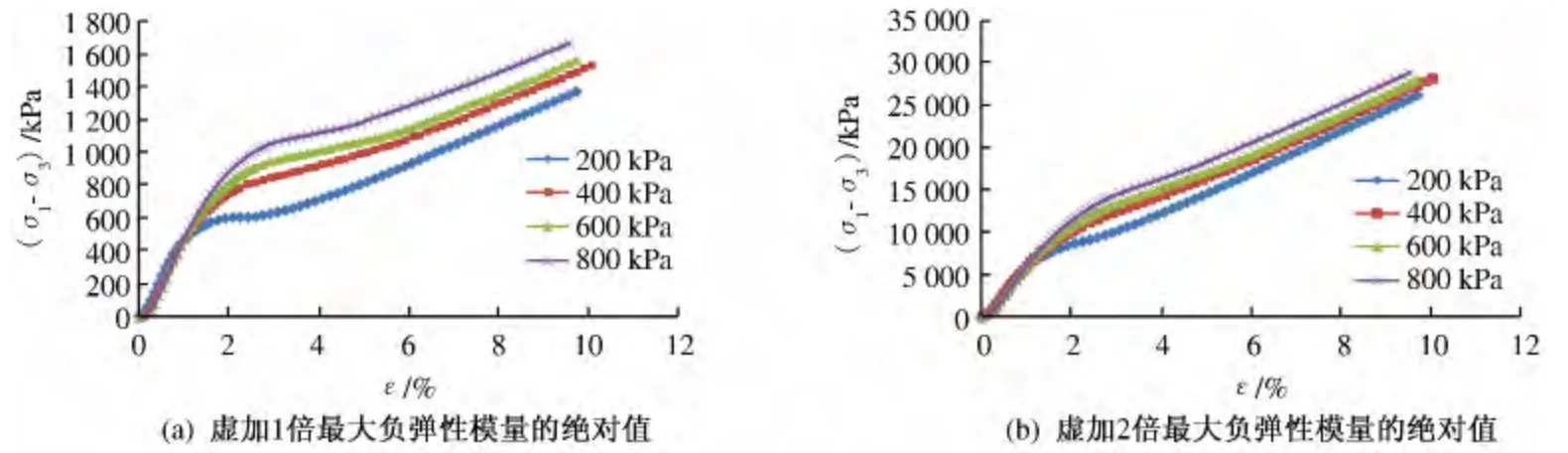
图3 虚加刚性弹簧后的应力-应变曲线
对于图3 中的应力-应变曲线,以ε 为横坐标,ε/(σ1-σ3)为纵坐标,在新的坐标系下的关系曲线如图4 所示.
由图4 可以看出,ε/(σ1-σ3)与ε 基本满足直线关系,用直线y =ax +b 进行拟合,其相关系数均在0.980 以上时,ε 对应的区间分别为1.58 ~3.74和1.50 ~4.08,在此区间内材料的抗剪强度达到最大值.
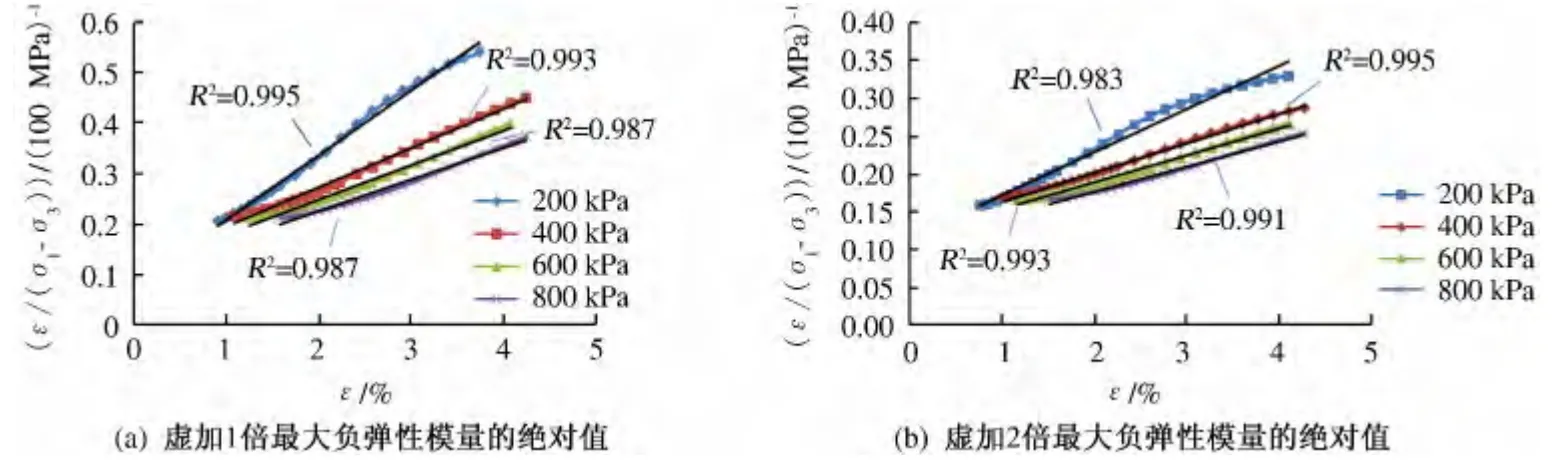
图4 ε/(σ1 -σ3)-ε 关系曲线
2.3 模型参数的确定
根据虚加刚性弹簧后的应力-应变曲线(图3),将模型参数的确定分为2 种情况:分别为虚加1 倍最大负弹性模量(情况1)和虚加2 倍最大负弹性模量(情况2),分析弹性模量对坝体应力及位移的影响,得到不同情况下坝体及坝基的参数,具体见表1.

表1 大坝模型参数
3 计算结果分析
3.1 应力分析
坝体的大主应力等值线如图5 所示,其中压应力为正,拉应力为负. 由图5 可以看出:大主应力分布趋势与一般堆石坝的大致相同,但高应力区略向下移动,在坝基面处;坝基面上的大主应力分布较为均匀,情况1 与情况2 的坝体的最大主应力σ1分别为1.13、1.14 MPa,出现位置均为坝底中部,说明弹性模量的大小对坝体大主应力的影响不大.
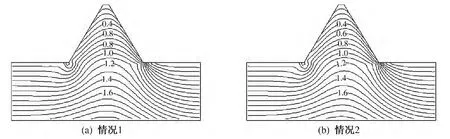
图5 坝体的大主应力σ1 的等值线图(单位:MPa)
坝体的小主应力等值线如图6 所示,其中压应力为正,拉应力为负. 由图6 可以看出,在不同情况下,小主应力分布趋势大致相同,在坝踵部位出现了局部拉应力,情况1 与情况2 下的坝体拉应力σ3分别为0.10、0.13 MPa,说明弹性模量的大小对坝体小主应力的影响不大.
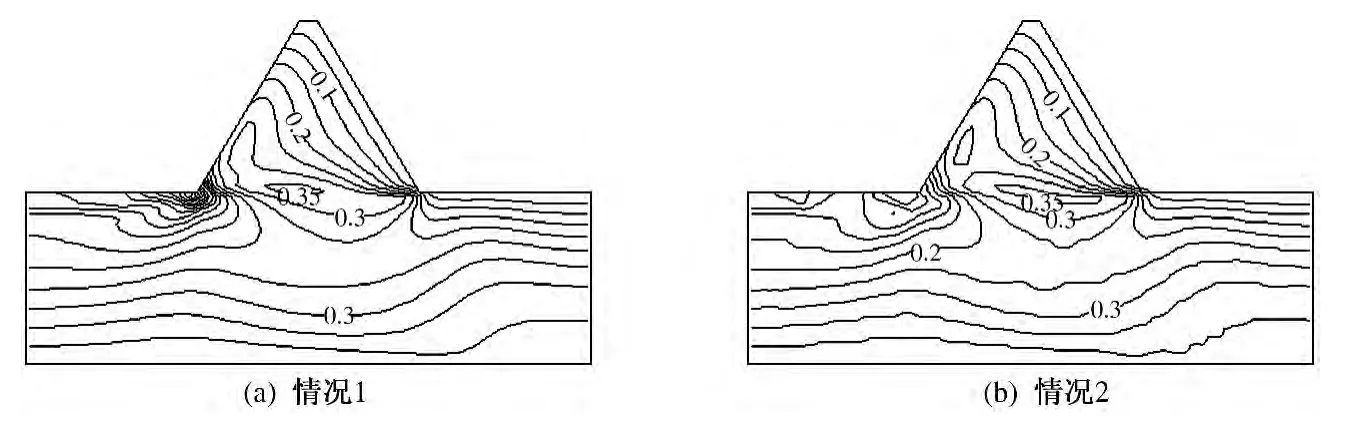
图6 坝体的小主应力σ3 的等值线图(单位:MPa)
3.2 位移分析
坝体的水平位移等值线如图7 所示.由图7 可以看出,在水压力的作用下,水平位移从坝基到坝顶呈逐渐增加的趋势,情况1 与情况2 下坝体的最大水平位移分别为3.93、5.13 cm,出现位置在坝顶上游侧.说明坝体的水平位移对弹性模量的影响比较敏感,但是对于坝高61.6 m 及坝顶宽6.0 m 来说,该影响还是比较小的.
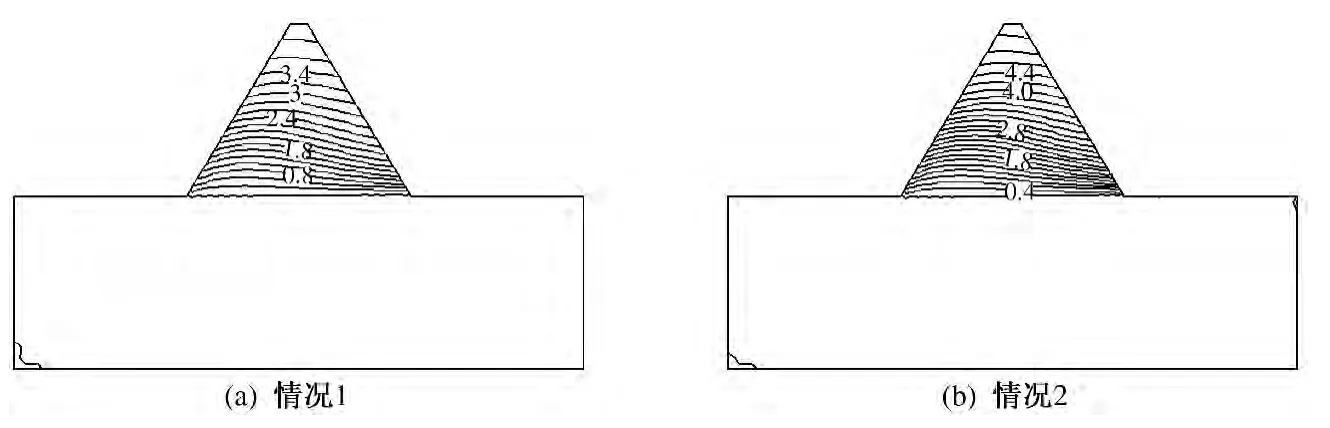
图7 坝体的水平位移的等值线图(单位:cm)
坝体的垂直位移等值线如图8 所示.由图8 可以看出,垂直位移等值线中心向下游方向移动,情况1 与情况2 下的坝体的最大垂直位移分别为2.84、3.65 cm,出现位置在1/2 坝高处.结合图7 可知,最大垂直位移大约为最大水平位移的60%,两者的大小与坡比有很大的关系.
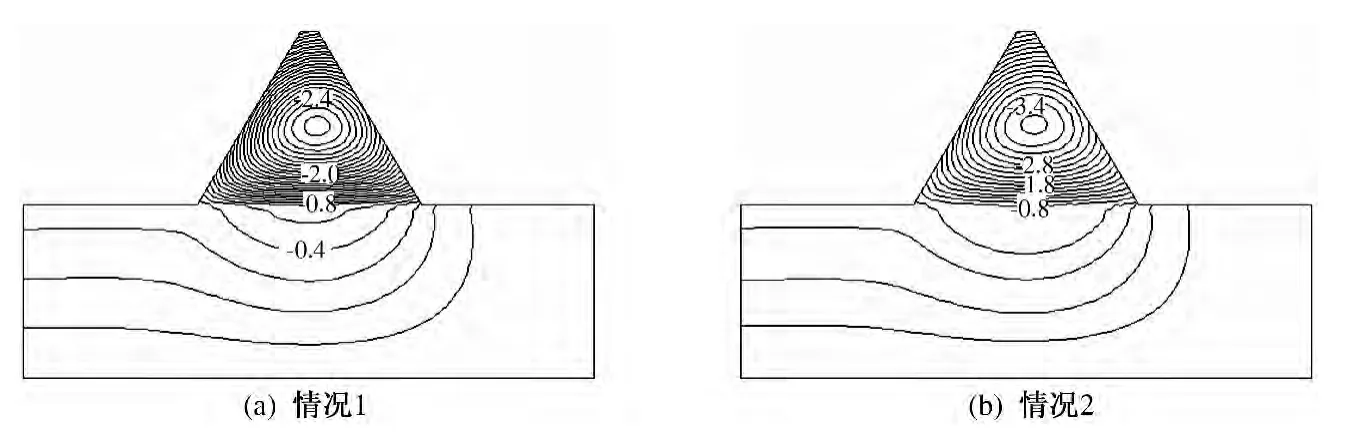
图8 坝体的垂直位移的等值线图(单位:cm)
4 结 语
在基于虚加刚性弹簧法建立的本构模型的基础上,对胶凝砂砾石坝体进行有限元分析,得到坝体的应力与位移等值线图. 由不同情况下的等值线图的对比分析可知,虚加最大负弹性模量绝对值的1 倍或2 倍,对坝体的应力和位移的总体影响不大,说明虚加刚性弹簧的弹性模量大小对坝体有限元分析结果的影响不大,虚加不同的弹性模量的目的在于解决应力-应变曲线的软化问题. 故基于虚加刚性弹簧法对胶凝砂砾石坝的有限元分析具有一定的可靠性.该成果为拟定合理的胶凝砂砾石坝剖面形式和控制标准提供参考.
[1]孙明权,刘运红,陈娇娇,等.胶凝砂砾石材料本构模型研究[J]. 华北水利水电学院学报,2012,33(5):13-15.
[2]孙明权,杨世锋,张镜剑. 超贫胶结材料本构模型[J].水利水电科技进展,2007,27(3):35 -37.
[3]孙明权,彭成山,陈建华,等.超贫胶结材料坝非线性分析[J].水利水电科技进展,2007,27(4):42 -45.
[4]吴梦喜,杜斌,姚元成,等.筑坝硬填料三轴试验及本构模型研究[J].岩土力学,2011,32(8):2241 -2250.
[5]李永乐,侯进凯,孙明权,等.超贫胶结混凝土力学特性试验研究[J].人民黄河,2007,29(3):59 -60.
[6]罗汀,姚仰平,侯伟. 土的本构关系[M]. 北京:人民交通出版社,2010.
[7]孙明权,杨世峰,柴启辉. 胶凝砂砾石坝基础理论研究[J].华北水利水电大学学报(自然科学版),2014,35(2):43 -46.

