基于GEO－Slope/W的土质高边坡稳定性分析

李风增

(1．郑州市公路管理局，河南 郑州 450003;2．河南省交通科学技术研究院有限公司，河南 郑州 450003)

对于天然或人工边坡，常由于自然或人为因素破坏其力学平衡，造成滑坡等地质灾害，严重威胁道路、建筑物或构筑物的安全，而任何有效的边坡加固措施均需确定边坡稳定系数和临界滑动面位置． 通常采用试算方法，根据工程区域所处的地质情况，假定若干可能滑动面，并逐个进行数值计算，确定最小稳定系数所对应的滑动面．近年来，业内学者采用多种数值模拟软件对边坡稳定性进行了深入分析，如邬爱清等［1－4］基于DDA 方法计算块体岩质边坡稳定;郑颖人等［5－9］通过有限元强度折减法，进行节理岩质边坡的稳定性计算;余志雄等［10－13］提出基于一种改进支持向量机算法(ν－SVR)的边坡稳定性预测方法，直接利用边坡特征参数快速预测边坡稳定性．上述已有成果中，以分析岩质边坡稳定性为主，且搜索潜在滑动面以折线居多．

GEO－Slope/W 软件是一个功能强大的边坡稳定性分析程序，其应用极限平衡理论，综合考虑地下水、土体裂缝、坡顶堆载等影响因素，能够对复杂土层、任意滑动面形状及多种孔隙水压力状况建立二维计算模型，用于研究土质高边坡的稳定性问题［14－16］．笔者应用GEO－Slope/W 软件对河南航空港区某办公区域土质高边坡进行稳定性分析，以确定其边坡稳定安全系数和滑动面位置，为边坡治理提供科学依据．

1 工程概况

某土质高边坡位于河南航空港区一老旧办公区域内，该边坡长约300 m，坡高约13 m，距塌方段约50 m 处修建有办公用房及停车场，外侧布置有一处幼儿园．原边坡支护措施为砖砌式挡墙，现已塌方，曾造成重大财产损失;墙体变形严重，分布有大面积贯穿性裂缝，上方土体主要为黄土状粉土．边坡顶部3 ～15 m 宽度范围内为长期堆积土，呈松散状态，孔隙较大．由于常年遭受雨水入渗，边坡土体含水量增大，土体抗剪强度大幅降低．在降雨冲刷和日照暴晒下，边坡表面沟壑丛生，雨水通过孔隙向纵深渗透，使得堆载土体随时有塌滑危险．该边坡为土质边坡，根据《建筑边坡工程技术规范》(GB 50330—2013)，边坡工程安全等级为一级．

2 模型建立

2．1 计算假设

由于坡体出现大量较长的纵向裂缝，经现场踏勘发现，可能存在潜在滑移面．根据边坡地质条件及滑动破坏特征，采用GEO－Slope/W 程序的Morgenstern－Price 法［17－18］建立计算模型，如图1 所示．

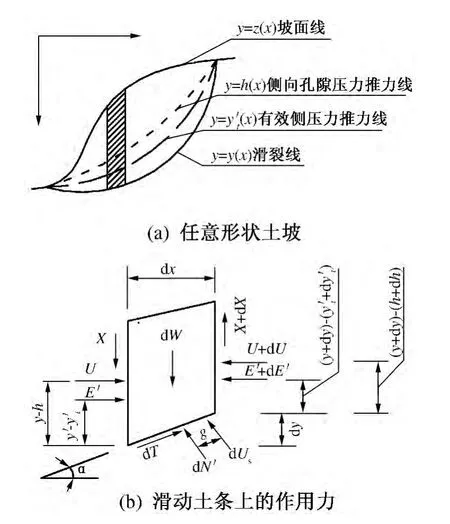
图1 Morgenstern－Price 法计算图式

图1(a)为任意形状的土坡，存在有自然坡面线y=z(x)、侧向孔隙水压力推力线y =h(x)和有效侧压力推力线y=y't(x)及潜在滑裂线y =y(x)．图1(b)为其中一个滑动土条dx，垂直方向作用有:滑条重力dW、切向条间力X、X +dX;水平方向作用有:土条两侧孔隙水压力U 及U+dU、土条两侧有效法向条间力E'、E' +dE';滑动土条底面作用有:有效法向反力dN'、切向阻力dT 以及孔隙水压力dUs．

Morgenstern－Price 法可对任意形状的滑裂面进行分析，故作如下假设:

1)假定滑裂面为任意形状，且两滑动土条的法向条间力和切向条间力之间存在关于水平方向坐标的函数关系．

2)每个土条均与土坡具有相同的稳定系数，当土坡处于稳定状态时，任一土条在滑动面上的抗剪力只发挥了一部分，并与此时的滑动力相平衡．

3)以滑动土条底部法向力和平行方向力以及土条底部中心点的力矩平衡建立力学方程．

2．2 计算参数

在综合分析土的物理力学参数的基础上，考虑在自然状态和饱和状态两种工况下建立计算模型，搜索计算出该剖面在此模型下的最危险圆弧滑动面及稳定系数．边坡地理位置及A'—A'、B'—B'剖面示意如图2 所示．

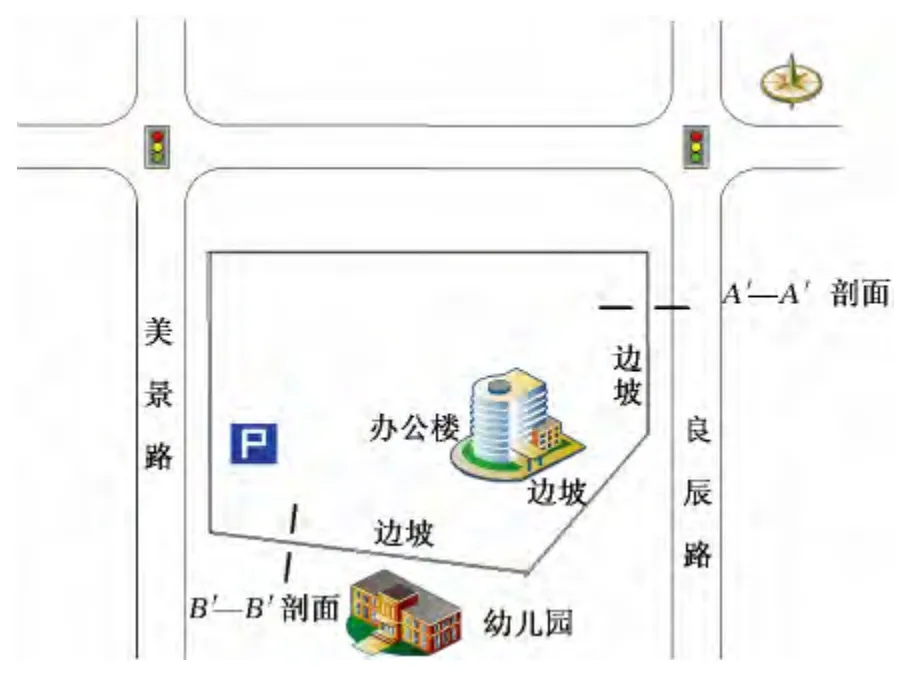
图2 边坡位置剖面示意图

取垂直于坡向的A'—A'、B'—B'剖面为边坡区域内的两个典型坡面，经现场勘察、取土样及室内试验，得出边坡土体的物理力学参数，见表1．

表1 土体物理力学参数表

2．3 计算模型

根据滑坡特点，设定一个可能产生圆弧滑裂面的圆心范围，画成正交网格，网格长可根据精度要求而定，网格交点即为可能的圆弧滑裂面的圆心，再设定滑弧深度在相对应的可行域范围内． 计算模型除坡面设为自由边界外，模型底部设为固定约束边界，模型四周设为单向边界，本构模型为Mohr －Coulomb模型的极限平衡求解．

边坡 A'—A' 剖面计算模型范围选取为15．0 m×7．5 m(长× 宽)，B'—B'剖面计算模型选取为36 m×13 m(长×宽)，其模拟的最危险滑动面均为圆弧面，其剪切口位于靠近滑坡坡脚附近．

3 GEO－Slope/W 模拟计算

GEO－SLOPE/W 程序的可视图形化界面可以清晰地看到最危险滑动面、对应的滑动中心位置(圆心)和相应的稳定系数，计算边坡稳定系数的效率高．

采用GEO－Slope/W 程序的Morgenstern－Price法，分析在自然状态和饱和状态两种工况下土质高边坡两个典型剖面A'—A'和B'—B'的最危险滑动面．

在两种工况下，A'—A'边坡剖面最危险滑动面、对应滑动中心位置和相应稳定系数模拟结果分别如图3 和图4 所示，计算所得两种工况下最小安全系数分别为0．840 和0．746．

图3 自然状态下A'—A'剖面最危险滑动面及稳定系数

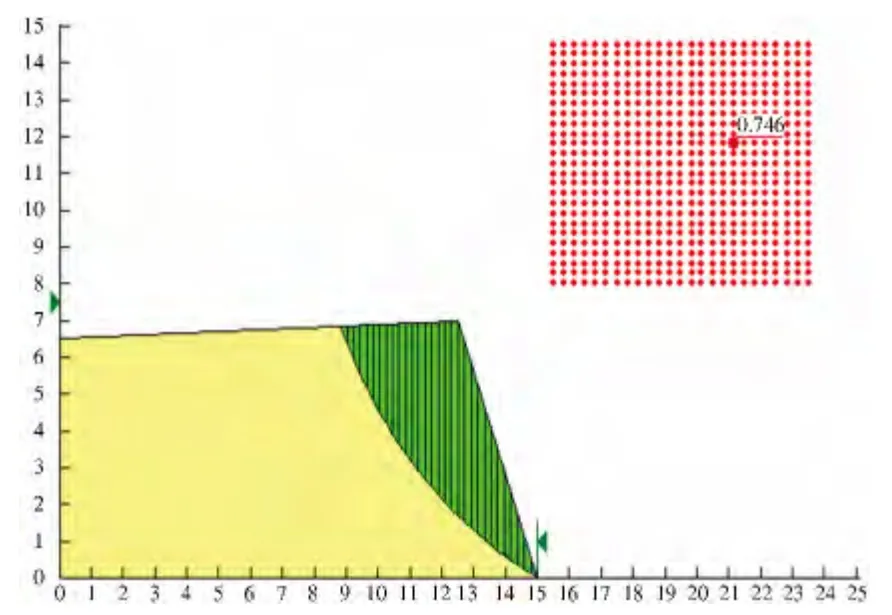
图4 饱和状态下A'—A'剖面最危险滑动面及稳定系数

在两种工况下，B'—B'边坡剖面最危险滑动面、对应的滑动中心位置(圆心)和相应安全系数模拟结果分别如图5 和图6 所示，计算所得两种工况下最小安全系数分别为0．721 和0．625．

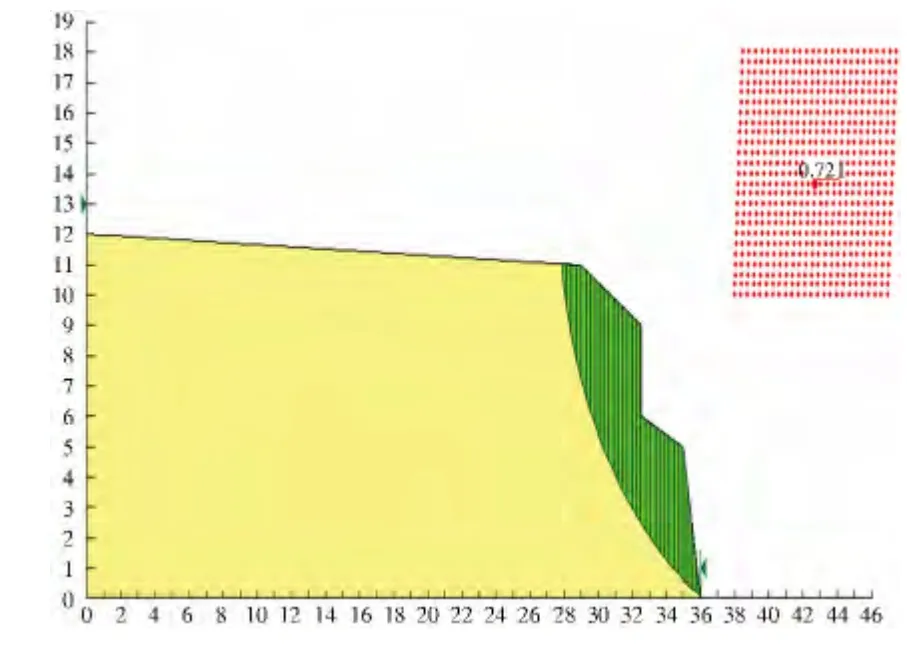
图5 自然状态下B'—B'剖面最危险滑动面及稳定系数

图6 饱和状态下B'—B'剖面最危险滑动面及稳定系数

边坡稳定性评价必须有一定的安全储备，考虑到国内稳定系数取值范围以及一级防护边坡安全需要，确定最终边坡的允许稳定系数为1．2 ～1．3．

由图3—6 可知，最危险滑动面为浅层滑动面，滑面近似圆弧形，在自然状态和饱和状态两种工况下，对于A'—A'剖面和B'—B'剖面所计算的稳定系数均小于边坡允许稳定系数，且饱和状态下的边坡稳定系数普遍比自然状态下降低0．10 ～0．11．说明土体含水量的增大加剧了边坡失稳的危险，边坡处于极不稳定状态．结合现场踏勘情况，该区域边坡出现顶部拉裂，坡角护墙变形、裂缝和大面积坍塌现象，所以急需实施混凝土挡墙加喷锚支护进行治理．

4 结 语

1)根据边坡稳定验算结果，两种工况下(自然状态下最小稳定系数为0．721、饱和状态下最小稳定系数0．625)边坡稳定系数均小于边坡允许稳定系数1．2 ～1．3，处于不稳定状态，该模拟状况与现场查勘的情况一致．

2)由于常年雨水的入渗增加了边坡的含水量，降低了土体的抗剪强度，增加了坡体自重和孔隙水压力，使边坡滑动面的抗滑能力降低;而边坡在饱和状态下的最小稳定系数比自然状态下降低0．10 ～0．11，也验证了含水量增大会加剧边坡的失稳危险．

3)从经济性和安全性方面来考虑，必须尽快对该边坡进行治理． 考虑到边坡高度、坡脚大小、坡度陡峭等因素，建议对A'—A'剖面所在边坡实施坡顶修建截水沟、坡体埋设排水管和坡脚修筑排水沟等防护措施;同时，用浆砌石加固坡脚，在坡面进行人工植草，防止雨水冲刷，杜绝土体达到饱和状态，降低土体含水量，以防边坡失稳．建议对B'—B'剖面所在边坡采用修建混凝土挡墙、加固边坡坡脚来提高土体抗滑力;在挡墙上部进行喷锚支护，防止雨水浸润;或者减载边坡顶部土体，在安全区域设置绿化景观，不仅提高边坡稳定性、防止黄土裸露污染空气，而且增加绿地、美化环境．

［1］邬爱清，丁秀丽，卢波，等．DDA 方法块体稳定性验证及其在岩质边坡稳定性分析中的应用［J］．岩石力学与工程学报，2008，27(4):664 －672．

［2］邬爱清，丁秀丽，李会中，等．非连续变形分析方法模拟千将坪滑坡启动与滑坡全过程［J］．岩石力学与工程学报，2006，25(7):1297 －1303．

［3］张润峰，张献民，陈国明． 基于DDA 的强度折减法求土坡安全系数［J］． 中国民航大学学报，2007，25(3):45－48．

［4］付晓东，盛谦，张勇慧． DDA 方法中的人工边界问题研究［J］．岩石力学与工程学报，2015，36(5):986 －993．

［5］郑颖人，赵尚毅．有限元强度折减法在土坡与岩坡中的应用［J］． 岩石力学与工程学报，2004，23(19):3381－3388．

［6］赵尚毅，郑颖人，邓卫东．用有限元强度折减法进行节理岩质边坡稳定性分析［J］．岩石力学与工程学报，2003，22(2):254 －260．

［7］江锋，李晓丽．非均质边坡稳定性分析的有限元强度折减法［J］．路基工程，2014(3):139 －142．

［8］吴应祥，刘东升，宋强辉，等．基于有限元强度折减法的边坡动力稳定性可靠性分析［J］． 岩土力学，2013，34(7):2084 －2089．

［9］陈寅春，胡文亮．基于有限元强度折减法多级边坡稳定性研究［J］．重庆交通大学学报(自然科学版)，2014，33(6):100 －103．

［10］余志雄，周创兵，李俊平，等．基于ν－SVR 算法的边坡稳定性预测［J］．岩石力学与工程学报，2005，24(14):2468 －2475．

［11］赵洪波，冯夏庭．支持向量机函数拟合在边坡稳定性估计中的应用［J］． 岩石力学与工程学报，2003，22(2):241 －245．

［12］李胜，韩永亮．基于MFOA－SVR 露天矿边坡变形量预测研究［J］． 中国安全生产科学研究，2015，11(1):11－16．

［13］漆祖芳，姜清辉，周创兵，等． 基于ν －SVR 和MVPSO算法的边坡位移反分析方法及其应用［J］． 岩石力学与工程学报，2013，32(6):1185 －1196．

［14］张丽珍，刘海欣．港珠澳大桥岛隧工程大圆筒结构边坡稳定性分析［J］．中国港湾建设，2015，35(6):9 －13．

［15］马恩帅，程建军，刘毅，等． 基于Quake/W 和Slope/W耦合方法的地震作用下水库边坡稳定性的分析［J］．石河子大学学报(自然科学版)，2015，33(2):244－251．

［16］吴启红，李文渊，明承林． 基于折现法滑动和Slope/W模拟的滑坡稳定性对比分析［J］．成都大学学报(自然科学版)，2011，30(2):134 －138．

［17］陈祖煜．土质边坡稳定分析:原理·方法·程序［M］．北京:中国水利水电出版社，2003．

［18］加拿大GEO－SLOPE 国际有限公司．边坡稳定分析软件SLOPE/W 用户指南［M］．中仿科技(Cn Tech)公司译．北京:冶金工业出版社，2011．