T－拟凸函数与严格T－拟凸函数的关系

胡 芳

( 武汉商贸职业学院 通识教育学院，湖北 武汉430205)

凸函数涉及很多数学命题的讨论证明和应用，在数学分析、函数论、泛函分析、最优化理论等应用研究方面应用非常广泛，具有重要的研究价值．随着凸性研究进一步深入发展，许多学者提出了弱化凸性的约束，构造更为广泛的凸性函数．拟凸函数是一类特殊的广义凸函数，1999 年，E．A．Youness 最先在Journal ofOptimization Theory and Application 上通过弱化凸集与凸函数的定义条件对它们进行了推广，定义了T－凸集，T－凸函数等概念［1］，得出了相关结论，并且提出了T－凸规划问题并对其进行了研究，虽然其中有一些结论是不正确的，但是其思想影响是非常深远的．2003 年，王建勇等人把T－凸函数推广到T－拟凸函数，并讨论了T－拟凸函数的一些性质［2］;2007 年，吴欧等人对文献［1］中的部分错误结论提出了反例，并进行了相应的修正，同时得到了T－拟凸函数与T－水平集之间的等价关系［3］，同年，宁刚在文献［4］中讨论了T－凸函数与T－拟凸函数的等价条件;2009 年，钟超瑾给出了T－凸集上的函数的半连续性与T－拟凸性之间的关系［5］;2011 年，文献［6］中讨论了在上(下)半连续的假设条件下，T－凸函数与T－拟凸函数的等价条件．文章充分考虑拟凸函数和T－拟凸函数、严格拟凸函数和严格T－拟凸函数可能存在的联系，分析T－拟凸函数和严格T－拟凸函数的关系，得到了某些新的结论，推广了文献［2，4，5］的主要结论．有关T－凸集，T－凸函数，T－拟凸函数，T－凹数，T－拟凹函数等的定义见文献［1－6］．

1 主要结论

引理1［5］若D是T－凸集，则T(D)⊆D．

定理1 设D⊂Rn凸开集，若存在线性映射T:Rn→Rn使得D是T－凸集且T(D)是凸集，f是定义在D上的n元实值严格T－拟凸函数，若∃α0∈(0，1)，∀x，y∈D有:

则f是D上的T－拟凸函数．

证明 反证法 假设∃x，y∈D，λ0∈(0，1)有:f［λ0T(x)+(1－λ0)T(y)］＞max{f(T(x))，f(T(y))}，

不失一般性，设f(T(x))≥f(T(y))，并令z=λ0T(x)+(1－λ0)T(y)，可知:

由引理1 可知:T(D)⊂D，则存在z0∈D，使得:T(z0)=z，即得:T(z0)=λ0T(x)+(1－λ0)T(y)，

若f(T(x))＞f(T(y))，由f是严格T－凸函数有:f(z)=f(T(z0))=f［λ0T(x)+(1－λ0)T(y)］＜max{f(T(x))，f(T(y))}=f(T(x))有:f(z)＜f(T(x))，这显然与式(1)矛盾．

(i)若0＜λ0＜α0＜1，此时，取，即有:

由f是严格T－拟凸函数、式(2)及式(4)，有:f(z1)＜max{f(z)，f(T(x))}=f(z)与式(4)矛盾．

(ii)若α0≤λ0＜1，由定理条件可知:α0≠λ0，因此有:0＜α0＜λ0＜1，从而，令即可得

由f是严格T－拟凸函数和式(2)以及上式，有:f(z2)＜max{f(z)，f(T(y))}=f(z)．

这与式(5)矛盾，故假设不成立．反过来，T－拟凸函数也可在一定条件下成为严格T－拟凸函数，这就是下述结果:

定理2 设D⊂Rn凸开集，若存在线性映射T:Rn→Rn使得D是T－凸集且T(D)是凸集，f是定义在D上的n元实值T－拟凸函数，若∃α0∈(0，1)，∀x，y∈D，当f(T(x))≠f(T(y))时，有:

则f是D上的严格T－拟凸函数．

证明 反证法．假设结论不成立，则∃x，y∈D，λ0∈(0，1)，虽然f(T(x))≠f(T(y))，但是仍然有:

不失一般性，不妨设f(T(x))＜f(T(y))，并令z=λ0T(x)+(1－λ0)T(y)，可知:

则式(6)变形为:

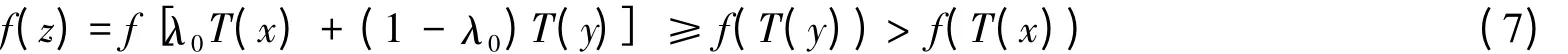
由f是T－拟凸函数有:

由D是T－凸集可知:z=λ0T(x)+(1－λ0)T(y)∈D，由定理条件及式(9)可得:

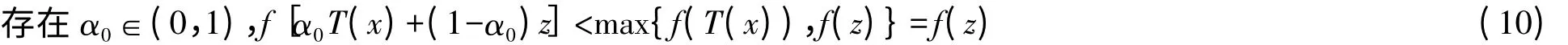
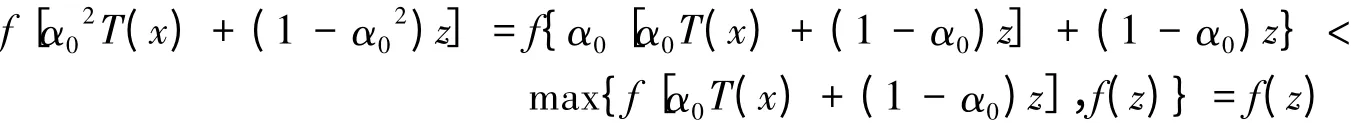
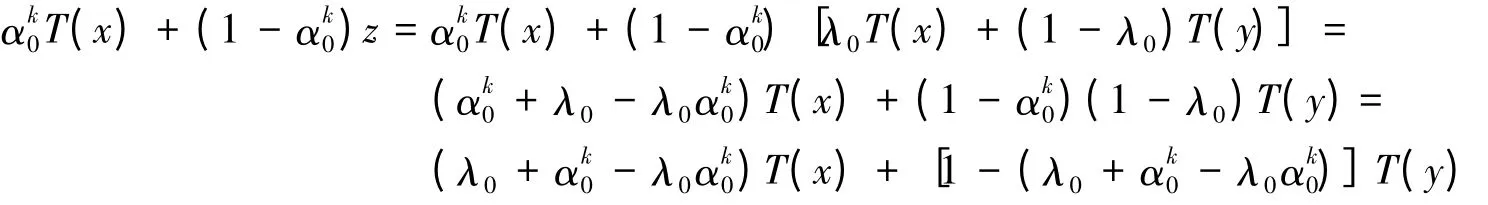
(i)若

由于

由式(14)及f是T－拟凸函数有)与式(13)矛盾．

(ii)若，由式(14)及定理条件，当)时有:

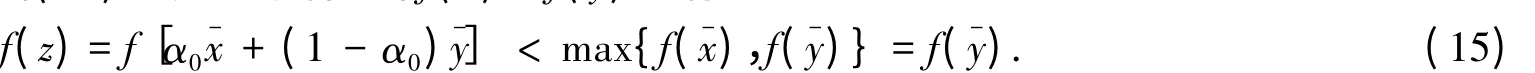
由f是T－拟凸函数有:

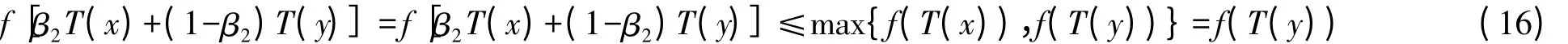
式(15)、式(16)可知:f(z)＜f(y－)≤f(T(y))与式(9)矛盾．

引理2［5］设D⊂Rn，若存在映射T:Rn→Rn使得D是T－凸集且T(D)是凸集，f是定义在D上的n元实值下半连续函数，且∃λ∈(0，1)使得:fλT(x)+(1－λ)T(y)

[]≤max{f(T(x))，f(T(y))，∀x，y∈D}．则f是D上的T－拟凸函数．

定理3 设D⊂Rn，若存在映射T:Rn→Rn使得D是T－凸集且T(D)是凸集，f是定义在D上的n元实值下半连续实值函数，并且存在λ0∈(0，1)，使得∀x，y∈D，f(T(x))＜f(T(y))均有:

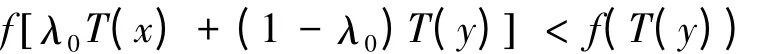
则f是D上的T－拟凸函数．

证明 由引理2，只需证明∀x，y∈D，存在相应的α∈(0，1)，使得:

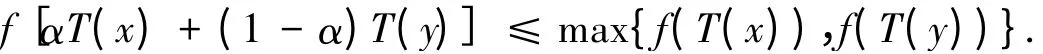
用反证法．假如存在x，y∈D，使得:

若f(T(x))≠f(T(y))，不妨设f(T(x))＜f(T(y))，由定理条件可知:

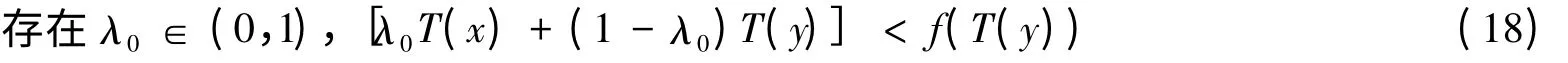
且在f(T(x))＜f(T(y))时，式(17)转化为存在x，y∈D，使得:f［λT(x)+(1－λ)T(y)］＞f(T(y))，∀λ0∈(0，1)，这与式(18)矛盾．

若f(T(x))=f(T(y))，式(17)变形为:存在x，y∈D，使得:

则有，选择合适的λ0可以有:

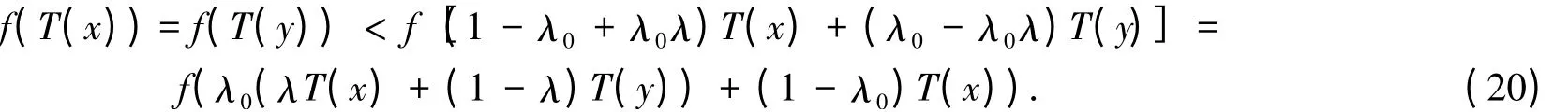
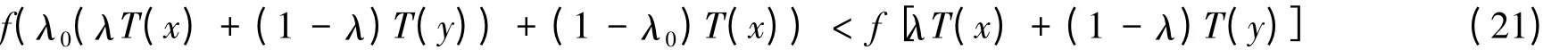
将式(20)运用定理条件可得:存在λ0∈(0，1)，

综合式(21)，式(22)可得:

定理3 的条件还可以进一步减弱，可得出定理4 如下．

定理4 设D⊂Rn，若存在映射T:Rn→Rn使得D是T－凸集且T(D)是凸集，f是定义在D上的n元实值下半连续实值函数，并且对∀x，y∈D，f(T(x))＜f(T(y))均有:

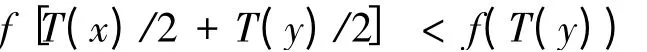
则f是D上的T－拟凸函数．

由定理3 和定理4 可以直接得出判定严格T－拟凸函数的另一种形式．

定理5 设D⊂Rn，若存在映射T:Rn→Rn使得D是T－凸集且T(D)是凸集，f是定义在D上的n元实值下半连续实值函数，并且存在λ0∈(0，1)，∀x，y∈D，当f(T(x))≠f(T(y))时，有:

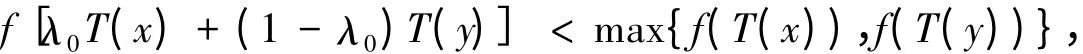
则f是D上的严格T－拟凸函数．

［1］ Youness E A．E－Convex Sets，E－Convex Function，and E－Convex Programming［J］．Journal of Optimization Theory and Application，1999，102(2):439－450．

［2］ 王建勇，宋颍，白咸伦．E－拟凸函数［J］．聊城大学学报:自然科学版，2003，16(3):17－19．

［3］ 吴欧，文乾英，杨玉红．关于E－拟凸函数几个错误命题的反例及修正［J］．重庆师范大学学报:自然科学版，2007，24(2):22－23．

［4］ 宁刚．E－凸函数的若干性质［J］．运筹学学报，2007，11(1):121－126．

［5］ 钟超瑾．E－凸集上的函数的半连续性与E－拟凸性［J］．广东教学学院学报，2009，29(3):48－51．

［6］ 韦丽，黄雪燕．E－凸函数和E－拟凸函数的等价条件［J］．数学的实践与认识，2011，41(15):191－197．

［7］ 杨新民．拟凸函数判别准则的一个注记［J］．运筹学学报，2001，5(2):55－56．