一个新超混沌系统的脉冲修正投影同步

程 杰，张 兰

( 重庆师范大学 数学学院，重庆401331)

混沌同步在物理、保密通信、生物系统、神经网络等领域中有着广泛的应用前景．近年来，脉冲控制被广泛应用于混沌系统的稳定与同步［1－5］，该种控制方法有以下优点:控制器的设计较简单，控制装置所需成本低，控制时所需能量少等．然而，在有关脉冲同步的文献中大多数是考虑脉冲完全同步和投影同步．2007 年，Li［6］把完全同步和投影同步推广到修正投影同步．当修正投影同步中的同步比例因子α1，α2，a3，α4分别取α1=α2=α3=α4=1 和α1=α2=α3=α4时即为完全同步和投影同步．

自1979 年以来一系列的超混沌系统被提出来，如超混沌Chen 系统、超混沌Lü 系统、超混沌Lorenz 系统等．2009 年，刘明华、冯久超［7］提出了一个新的超混沌系统:

其中x1，x2，x3，x4是状态变量，当参数a=35，b=3，c=35，而d∈(4．6，29．2］和d∈(33．5，53．7］时，系统(1)有两个正的Lyapunov 指数，是超混沌系统．

本文对超混沌系统(1)进行脉冲控制后得到脉冲微分系统，然后运用脉冲比较系统方法，得到了脉冲修正投影同步的充分判据．

1 基本定义与预备知识

一个脉冲微分系统如下描述［8］:

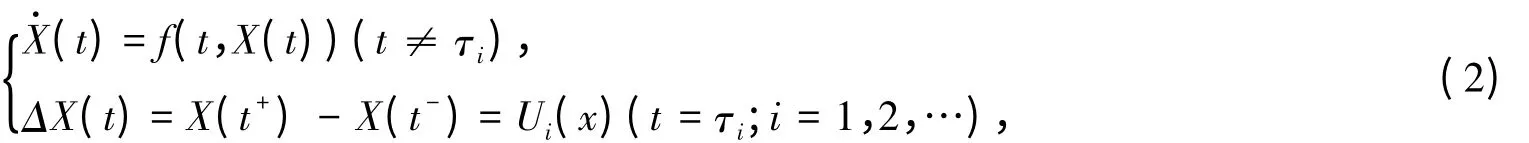
这里X∈Rn是状态变量，f:R+×Rn→Rn连续，Ui:Rn→Rn是状态变量在时间瞬时τi的改变换言之和分别定义为τi前后的瞬时．{τi:i=1，2，…}满足当i→∞时．

2 主要结果

把方程(1)所刻画的混沌系统的线性部分与非线性部分分开，重写如下:

这里x=(x1，x2，x3，x4)T，且:

在脉冲同步构造模型中，驱动系统由(3)式确定，由于在离散时刻τi(i=1，2，…)，驱动系统的状态变量被传送到响应系统，因此响应系统的状态变量会经历一个瞬时的跳跃．所以受控的响应系统为:

{τi:i=1，2，…}满足:

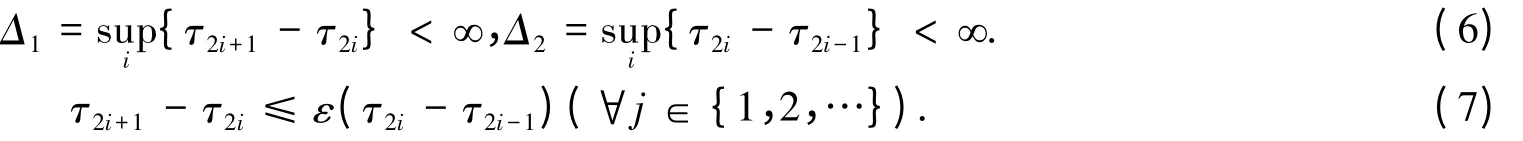
令φ(x，y)=φ(x)－αφ(y)，则:

则脉冲投影同步的误差系统为:

由于混沌系统的状态变量是有界的，因此存在正数Mi(i=1，2，3，4)使得|xi(t)|≤Mi，|yi(t)|≤Mi对所有的t成立，从而有如下定理．

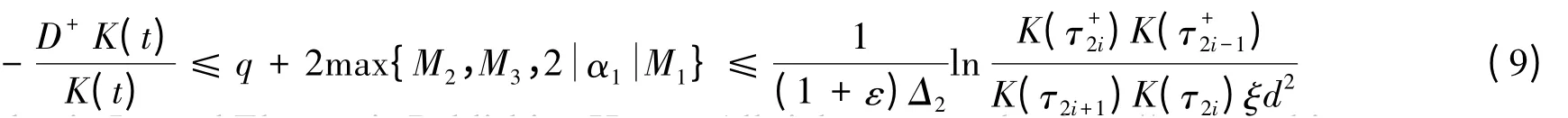
或者:

则误差系统(8)的平凡解是渐近稳定的，也蕴含着系统(3)与(5)的脉冲修正投影同步是渐近稳定的．

证明 取Liapunov 函数V(t，e)=eTe，当t≠τi时，有:

当t=τi时，有:

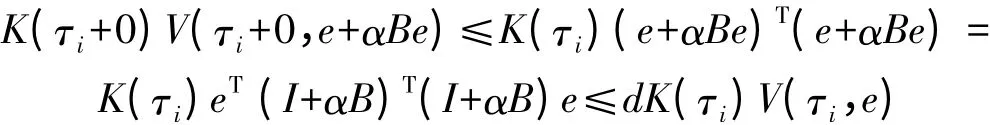
由文献［9］可知系统(8)的渐近稳定性可由如下比较系统来判定:

其中，上述两不等式成立的原因是因为定理中的不定式(9)和(10)，因此由文献［9］中的相应定理可知系统(8)的平凡解是渐近稳定的．

注1 :若令:

则可得:

这表明当同步因子α=diag(α1，α2，α3，α4)满足方程(12)时，不需要控制器U也能够实现脉冲修正投影同步，从而本文所给方法可以看做是脉冲完全同步的推广(α4≠0)．

注2:通过定理1，可估计出脉冲间隔Δ2的上界:

3 结论

本文研究了一个新超混沌系统的脉冲控制与修正投影同步问题，在脉冲间隔变化的情况下得到了保证脉冲控制系统修正投影同步的充分判据，也可得到脉冲区间Δ 的上界估计．

［1］ Yang T，Yang L B，Yang C M．Impulsive synchronization of Lorenz systems［J］．Phys Lett A，1997，226(6):349－354．

［2］ 罗润梓．一个新混沌系统的脉冲控制与同步［J］．物理学报，2007(56):5655－5660．

［3］ Zhao Y H，Yang Y Q．The impulsive control synchronization of the drive－response comples system［J］．Physics Letters A，2008，372:7165－7171．

［4］ Liu G M，Ding W．Impulsive synchronization for a chaotic system with channel time delay［J］．Commun Nonlinear Sci Numer Simulat，2011，16:958－965．

［5］ Sun Jitao，Wu Qidi．Impulsive control for the stabiliztion and synchronization of Lure system［J］．Applied Mathematics and Mechanics，2004，25(3):291－296．

［6］ Li G H．Modified projective synchronization of chaotic system［J］．Chaos Solitons Fractals，2007，32:1786－1790．

［7］ Liu Minhua，Feng Jiuchao．A new hyperchaotic system［J］．Acta Physica Sinica，2009，58(7):4457－4462．

［8］ Lakshmikantham V，Bainov D D，Simeonov P S．Theory of Impulsive Differential Equations［M］．Singapore:World Scientific，1989．

［9］ Sun J T，Zhang Y P，Wu Q D．Less conservative conditions for asymptotic stability of impulsive control systems［J］．IEEE Trans Automatic Contr，2003，48(5):829－831．