医学装备突发故障预测方法的研究

丛 晋 李丙所 马国平

医学装备突发故障预测方法的研究

丛 晋①李丙所①马国平①

目的：对医学装备突发故障预测方法进行研究，以保障远离基地的海上医疗需求。方法：根据医学装备的突发故障数据的表现，对医学装备出现突发故障的时间、随机变量及分布类型进行假设，并对其进行参数估计和分布拟合检验，确定医学装备的突发故障密度函数。结果：基于故障数据分布函数建立医学装备突发故障预测模型，获得医学装备未来一段时间内的突发故障概率。结论：通过医学装备突发故障实例分析，验证了突发故障预测模型的合理性。

医学装备；故障预测；故障数据；数理统计

DOI∶ 10.3969/J.ISSN.1672-8270.2015.11.011

[First-author’s address] Naval Hospital in Yantai, Yantai 264001, China.

随着海军远离基地依托的海上医疗保障任务的日益增多，保障在任务期内医学装备良好的运行状态是圆满完成海上医疗的重要环节。电子医学装备的故障通常是由其内在失效机制与外部环境因素综合作用所导致，其过程极为复杂。医学装备故障的发展进程可分为突发故障与退化故障两种[1-4]。突发故障表现为医学装备的各项监测参数数据在使用过程中一直保持在合格范围内，但在某一时刻则突然超出规定阈值。对于多数的电子设备而言，故障均属于突发故障。

1 医学装备突发故障数据分布类型

对于经常使用的医学装备，其故障数据可表现为设备出现故障的时间。由于医学装备突发故障其故障时间是一个随机变量，因此可以假设设备的故障时间t服从一维分布F(t，a)，其中a=(a1,a2…，ak)，是该分布的参数向量，且其一维密度函数f(t，a)存在，则为公式1：

由一般密度函数的性质及故障数据的物理特性可知，f(t，a)应满足对任意的t，。由于分布F(t，a)的自变量t为医学装备使用时出现故障的时间，根据故障数据得到的分布参数向量a为确定值，不随时间而变化。因此，如果确定了F(t，a)的分布类型，基于故障数据估算出参数向量a的估计量，即可确定故障数据的分布函数F(t，)。由于F(t，a)未知，因此可根据工程经验假定其可能分布类型，如指数分布、正态分布及 Γ分布等，并对其进行参数估计以确定F(t，a)的具体形式，同时尚需要进行分布拟合检验，以验证假设是否成立[5-6]。

对于医学装备的故障时间，根据工程经验通常假定其服从指数分布，分布密度函数可表示为公式2：

式中λ为医学装备的平均故障率，此时故障数据的分布参数向量a=(λ)。由指数分布的性质可知，平均故障率λ和平均寿命θ互为倒数。

2 医学装备突发故障数据分布统计推断

2.1 故障数据分布参数极大似然估计

如果根据工程经验对故障数据的分布类型进行假设，可以认为故障数据的分布类型是已知的，只是分布的参数未知，可根据样本的数据对总体的分布参数进行估算，即数理统计中的参数估计问题。为了确定分布参数的估计量，可以采用极大似然估计法[7]。

对于抽样的一批医学装备，由于采用修复性维修，因此每次测试时样品总数不变，可看作是有替换的定时截尾试验。假设对抽样的n台医学装备进行了m次测试，每次测试时设备的故障数为ri(i=1，…，n)，则该医学装备的总测试时间为n台设备测试m次的时间，可表示为公式3：

平均寿命θ的极大似然估计为公式4：

如果某医学装备的故障时间(平均寿命)服从指数分布，则故障率λ的极大似然估计量可表示为公式5：

式中λ为λ的无偏估计。

2.2 故障数据分布拟合检验

对于故障数据，根据工程经验假定其可能分布类型后，还需要对其进行假设检验，以验证假设是否成立。假设检验分为参数检验和非参数检验，当总体分布类型已知，只对某些参数的假设进行的检验称作参数检验，对其他假设作出的检验称作非参数检验。由于医学装备故障数据的分布类型未知，需根据工程经验对其假设，并利用样本数据进行检验，因此属于非参数假设检验。

判断总体是否为某种分布(如正态分布)的检验，统称为分布的拟合优度检验，简称分布拟合检验。常见的分布拟合检验有x2分布拟合检验和K-S拟合检验。当总体为一维且理论分布完全已知时，Копмогоров检验(K检验)优于x2检验，因此考虑采用K检验法。

2.2.1 K检验

K检验的原理是：首先考虑检验假设H0∶F(x) =F0(x)，式中F0(x)为完全已知的连续型分布函数。

当样本容量n充分大时，经验分布函数Fn(x)与总体分布函数F(x)相当接近。因此，当H0成立且n较大时，Fn(x)与F0(x)的差距不应太大。鉴于此，俄国数学家Копмогоров提出用统计量：

作为H0的检验统计量。

由于Fn(x)与F0(x)都是x的单调非降函数，所以偏差 Fn(x)-F0(x) 的上确界可在n个点X(i)处找，因而K检验是先在样本的每个顺序统计量X(i)上求经验分布函数和假设的分布函数之间偏差较大的一个，即为公式6：

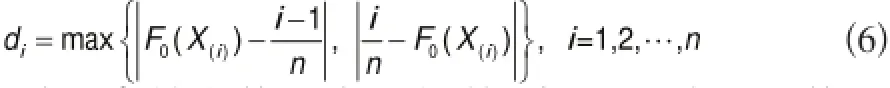
而这n个di中最大的一个，就是K检验统计量Dn的取值，即为公式7：

若Fn(x)与F0(x)拟合得好，则Dn的值应比较小；反之，当Dn较大时，Fn(x)与F0(x)拟合得不好。因此，K检验的规则是：对于给定的显著性水平a，若Dn＞Dn，a，则拒绝H0，否则接受H0。其中n＜100时，Dn，a可查K检验临界值表获得。

当样本X1，X2…，Xn中无重复数据时，可按公式(6)和公式(7)计算Dn的值。而当样本X1，X2…，Xn中有重复数据时，可如下进行：先将样本X1，X2…，Xn从小到大排列(重复数据合并为一个)X(1)＜…＜X(m)，(1≤m≤n)，设ni为对应X(i)在样本中出现的频数，则有ni≥1，n1+n2+…+nm=n其中Fn(X(m+1))=1。令其为公式8：

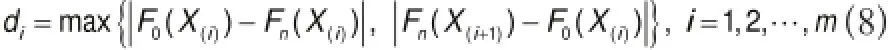
此时为公式9：

2.2.2 指数分布检验

假设对抽样的n台医学装备进行了m次测试，每次测试时样品的故障数为ri(i=1，…，n)，则医学装备的故障时间可表示为Tij(i=1，…，n；j=1，…，m)，因此检验该医学装备的故障时间是否服从指数分布，是根据测试得到的故障时间样本T1，…，Tp(p≤nm) (重复的数据合并为一个)检验总体的分布是否服从单参数指数分布。由于单参数指数分布函数F0(t)=1-e-λt，t＞0中包含未知参数λ，如果用λ的极大似然法估计来代替λ，则要检验的假设实际上为H0∶F(t)=F0(t；λ^)=1-e-λ^t，t＞0，同样可取检验统计量，其为公式10：

式中

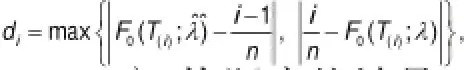
(T

(1)

，T

(2)

…，T

(p)

)是 (T

1

，T

2

…，T

p

) 的顺序统计量。当样本中有重复数据时，与前面的求法相同。

为提高检验功效，Finklestein和Schafer提出检验的统计量为公式11：

3 医学装备突发故障预测模型

随着使用时间的增加，医学装备可能会突发故障[8-11]。由于突发故障发生时间短且故障前无明显征兆，因此可以考虑利用故障数据来统计分析其故障规律。通过对医学装备历年测试、使用信息的整理，发现其故障数据均表现为设备出现突发故障的时间，因此可以基于故障数据对医学装备的突发故障进行预测。由于医学装备的突发故障时间是一个随机变量，因此根据工程经验对其可能分布类型进行假设，并对其进行参数估计和分布拟合检验，即可确定医学装备的突发故障密度函数，此时故障数据的分布参数是一个不随时间变化的常数。根据故障密度函数的定义，医学装备在0到t时间段内发生突发故障的概率即为该时间段内突发故障密度函数下所围的面积，如图1所示[12-13]。

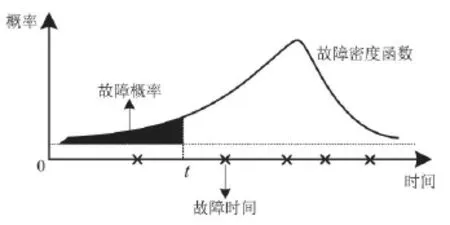
图1 突发故障密度函数曲线图

设医学装备突发故障密度函数为f(t，a)，T为医学装备突发故障前时间，则医学装备在0到t时间段内发生突发故障的概率为公式12：

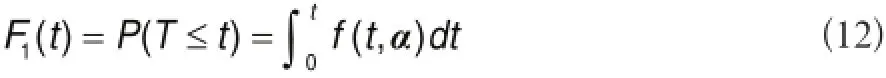
如果要预测医学装备在t到t+Δt(Δt＞0)时间段内的突发故障概率，则是一个条件概率事件，即在0到t时间段内医学装备未发生突发故障的条件下，对医学装备在t到t+Δt时间段内发生突发故障的概率进行预测，此时医学装备的突发故障概率为公式13：

如果医学装备的突发故障时间服从指数分布，则突发故障密度函数可表示为f(t，a)=λe-λt，t＞0，由公式(12)和公式(13)可知，医学装备在0到t时间段内发生突发故障的概率为F1(t)=P(T≤t)=1-e-λt，在t到t+Δt时间段内发生突发故障的概率为F1*(t)=P(t＜T≤t+Δt T＞t)=1-e-λΔt，即医学装备在任意Δt时间间隔内发生突发故障的概率等于在0到Δt时间段内发生突发故障的概率，体现了指数分布的无记忆性。

医学装备进行突发故障预测时，由于基于故障数据得到的分布参数向量为一确定值，不随时间变化，因此只需对医学装备的故障数据进行统计推断，确定其突发故障密度函数，即可根据公式(12)和公式(13)对医学装备的突发故障概率进行预测。同时，由于目前对某些大型医学装备需进行定期维护、测试，因此医学装备在未来某时刻的突发故障概率等于未来该时刻相邻两次维护、测试时间段内的突发故障概率[14-15]。

4 医学装备突发故障案例分析

以使用中的整批某种医学装备为研究对象，随机抽取10台医学装备作为样本进行分析。由于该批医学装备采取定期维护、检测方式，从2002年开始，每年维护、测试一次，维护、测试信息记录至2009年，因此可根据2002-2007年的故障数据，对该医学装备2008年和2009年的故障概率进行预测，并将预测结果与实际故障情况进行对比，以检验医学装备突发故障预测模型是否合理。

4.1 故障数据分布类型的确定

根据工程经验可假设医学装备的故障数据服从指数分布。通过对医学装备2002-2007年的故障数据进行整理，发现抽取的10台医学装备在2003-2007年使用时发生故障且均为突发故障，故障个数分别为1，1，1，2，2。由于对该批医学装备进行定期维护、测试，每年维护、测试1次，若以年为时间单位，则医学装备的突发故障时间可表示为2，3，4，5，5，6，6。设医学装备的故障数据为T，需检验T是否服从指数分布，即检验假设H0∶T～F(t；λ)=1-e-λt，t＞0是否成立。

由公式(5)可得该医学装备故障数据分布参数向量的极大似然估计量为：

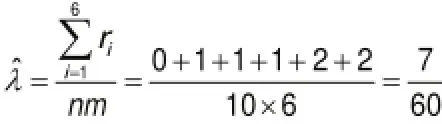
将该医学装备的故障数据按从小到大的顺序排列(重复的数据合并为一个)，对其进行K检验，计算过程见表1。

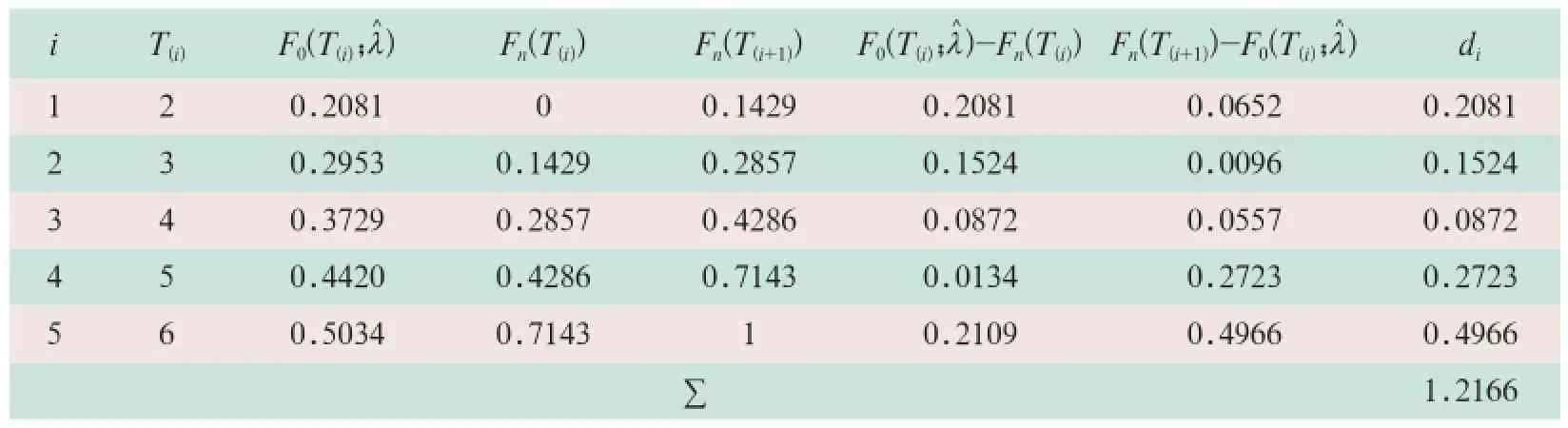
表1 医学装备故障数据的指数分布检验

4.2 故障预测结果分析

由故障数据分布类型计算可知，医学装备的故障数据服从指数分布，故障密度函数为分布参数。由于λ是一个常数，不随时间变化，因此根据公式(13)即可对该医学装备在2008年内发生突发故障的概率进行预测。由指数分布的无记忆性可知，医学装备在2008年内发生突发故障的概率即为2008-2009年内发生突发故障的概率(维护、测试时间间隔为1年)，即：

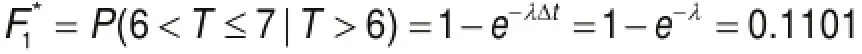
同理，对该批医学装备2009年的突发故障概率进行预测，结果为0.1247。根据实际观测记录结果，该批医学装备在2008年和2009年发生突发故障的概率均为0.1，预测结果和评估结果基本一致，可以认为医学装备突发故障预测模型合理。

5 结论

在一定置信度的前提下，基于故障数据的统计分布规律，对医学装备突发故障预测方法进行了研究，对医学装备的突发故障进行预测时，由于故障数据的分布参数为一常数，不随时间变化，因此通过统计推断确定故障数据的分布规律后，即可基于故障数据分布函数建立医学装备突发故障预测模型，对医学装备未来一段时间内的突发故障概率进行预测，其预测结果为医学装备离岸前维修保障提供了依据，且可对保证海上医疗保障任务期内设备的良好运行提供重要支撑。

[1]杨瑞峰.医学装备维修技法探讨[J].医疗卫生装备，2009，30(3)：131-132.

[2]刘鸾.医院医学装备的维护与使用[J].内蒙古中医药，2013(9)：113-114.

[3]崔骊，李向东，云庆辉.医学装备质量控制管理面临的问题与对策[J].中国医学装备，2013，10(1)：74-75.

[4]张红侠，刘勇，卢中凯.关于提高医学装备维修效能的探讨[J].中国医学装备，2013，28(3)：105-106.

[5]Baruah P，Chinnam RB.HMMs for diagnostics and prognostics in machining processes[J]. International Journal of Production Research，2005，43(6)：1275-1293.

[6]Chinnam RB，Baruah P.A neuro-fuzzy approach for estimating mean residual life in condition-based maintenance systems[J]. International Journal of Materials and Produce Technology，2004，20：166-179.

[7]吴翊，李永乐，胡庆军.应用数理统计[M].北京：国防科技大学出版社，2008：112-120.

[8]张红侠，刘勇，卢中凯.浅谈医学装备维修[J].医疗装备，2013，28(3)：105-106.

[9]黄鑫，刘尚军.现代医疗大型医院设备维修存在问题与对策探讨[J].医疗卫生装备，2012，33(12)：103-105.

[10]张宜江，焦明阳.浅谈医学装备管理中的预防性维护[J].中国医学装备，2012，9(11)：79-82.

[11]文彬，邱丹.医学装备维修方式进展[J].中国医学装备，2011，8(10)：92-94.

[12]Feldman K，Jazouli T，Peter A，et al.A Methodology for determining the return on investment associated with prognostics and health management[J].IEEE Transactions on Reliability，2009，58(2)：305-316.

[13]Ramakrishnan A，Pecht MG.A life consumption monitoring methodology for electronic system[J].Components and Packing Technologies IEEE Transactions on，2003，26(3)：625-634.

[14]韩承军.论医学装备维修技术要点[J].电子制作，2013，5(8)：233-234.

[15]陈锐新.浅谈医学装备维修管理模式与实践[J].医疗装备，2014，27(3)：82-83.

[16]张金堂，董霞.利用高科技手段开展维修提高医疗设备完好率[J].中国医学装备，2014，11(10)：114-116.

Research on prediction method of medical equipment sudden fault

CONG Jin, LI Bing-suo, MA Guo-ping
China Medical Equipment,2015,12(11)∶33-36.

Objective∶ To do research on prediction method of medical equipment sudden fault for the requirement of medical security at sea which is away from base. Methods∶ Sudden fault data of the medical equipment is a random variable which often manifest as the time of sudden fault happening. The possible distribution type of fault data is hypothesized according to the engineering experience. In order to ensure the sudden fault density function of medical equipment, parameter estimation and distribution fit test are carried out for the fault data. Results∶ The sudden fault prediction model of medical equipment is established to get the future sudden fault probability of medical equipment based on the distribution function of fault data. Conclusion∶The results of case analysis validate the rationality of sudden fault prediction model.

Medical equipment; Fault prediction; Fault data; Mathematical statistics

丛晋，男，(1960- )，本科学历，副主任医师。海军烟台医院院长，从事医院管理工作。

1672-8270(2015)11-0033-04

R197.39

A

2014-12-15

①海军烟台医院 山东 烟台 264001