双无人机协同定位远程测距误差分析

胡天翔

摘 要：该文通过安置相差定位设备近程观测站的方式，将所测得低精度的测距数据应用几何关系转换到后方观测站，当前哨观测站和后方观测站之间的距离满足数据计算需要时，可实现后方观测站对目标的远程高精度测距，从而实现双机协同侦察与测绘的工作。

关键词：无人机 双站定位 相差定位 测距

中图分类号：TP273 文献标识码：A 文章编号：1674-098X（2015）09（c）-0044-02

Double UAV Cooperative Localization and Remote Location Error Analysis

Hu Tianxiang

（College of Mechatronic Engineering，Nanjing Institute of Industry Technology，Nanjing Jiangsu，210023，China）

Abstract：In this paper，through the placement phase positioning equipment short-range observation station， the measured data of the geometric relationship of low precision ranging applications into the rear observation station，the current post observation station and the distance between the rear observation station to meet data calculation need，can realize the rear observation station of the remote high precision ranging targets，so as to achieve double cooperative reconnaissance and mapping work.

key Words：UAV；Double station location；Difference location；Distance Measurement

机载电站无源定位技术在定位测星精度等方面还有待改善，尤其为实现远程高精度定位目前可能还有困难，即使是采用多机协同时差定位方法也具有一定的技术难度。根据现有的误差分析理论，多站时差定位系统站间的基线长度至少必须大于十几公里，为获得较好的定位精度，往往需要几十公里长。由此就会产生诸多的问题：（1）对高重频信号的定位模糊性；（2）多站不能同时探侧获得目标的窄波束信号。

与相差干涉测向不同，利用短基线的相差定位是难以得到好的定位精度的。尽管采用较长基线的多站相差定位能够实现远距高精度定位，但要應用于机载系统还有许多技术难题需要解决。作为一种探讨，本文提出了一种前后相隔较大距离的双机协同无源定位方法，其中，近程接近敌方目标的前方观测站可以是采用简单的短基线相差测量技术的无人机。后方观测站的可以是有人战斗机，现有的数学模型已证明，借助于前后双站间的长基线，可实现后方观测站对目标的远程高精度测距。但远程高精度测向问题还有待研究。

1 相差定位

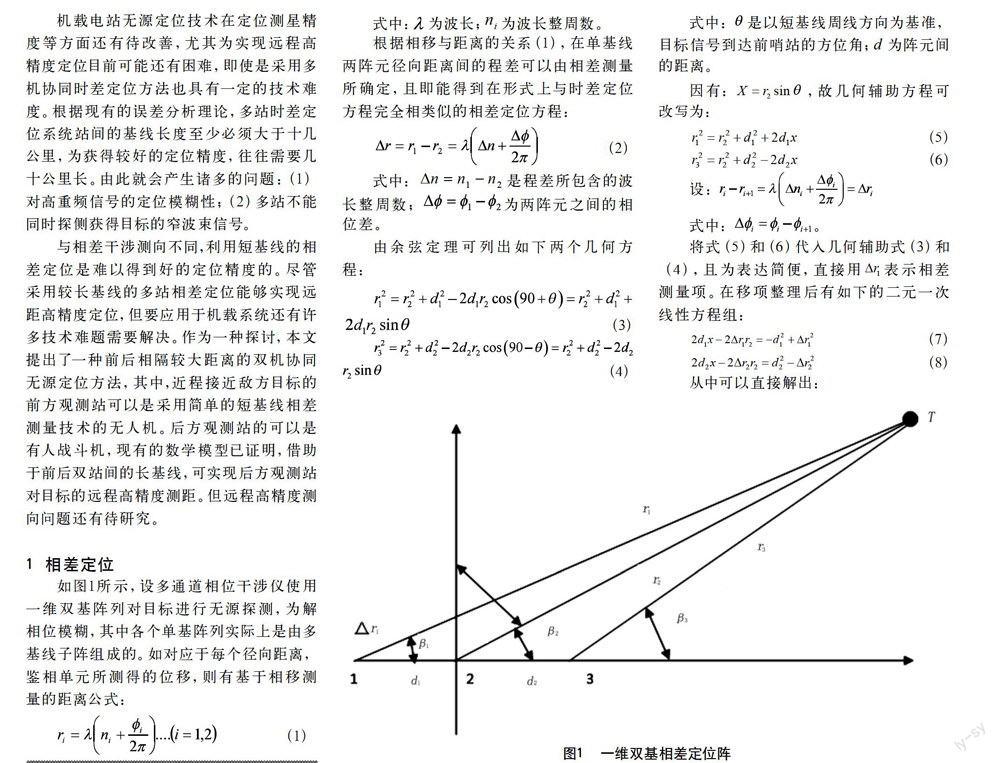
如图1所示，设多通道相位干涉仪使用一维双基阵列对目标进行无源探测，为解相位模糊，其中各个单基阵列实际上是由多基线子阵组成的。如对应于每个径向距离，鉴相单元所测得的位移，则有基于相移测量的距离公式：

（1）

式中：为波长；为波长整周数。

根据相移与距离的关系（1），在单基线两阵元径向距离间的程差可以由相差测量所确定，且即能得到在形式上与时差定位方程完全相类似的相差定位方程：

（2）

式中：是程差所包含的波长整周数；为两阵元之间的相位差。

由余弦定理可列出如下两个几何方程：

（3）

（4）

式中：是以短基线周线方向为基准，目标信号到达前哨站的方位角；为阵元间的距离。

因有：，故几何辅助方程可改写为：

（5）

（6）

设：

式中：。

将式（5）和（6）代入几何辅助式（3）和（4），且为表达简便，直接用表示相差测量项。在移项整理后有如下的二元一次线性方程组：

（7）

（8）

从中可以直接解出：

（9）

（10）

由求得的目标位置参数，即能得到目标的到达角：

（11）

注意，符号实际上表示的是相位测量项：，即到达角是由相差测量得到的。当相邻基线相等时有：

（12）

（13）

2 远程测距方程

设基于一维双基相差前方进近探测站为后方远程探测站，前后两站间的几何关系如图1所示，直接利用余弦定理可得到远程观测站到目标的距离：

（14）

式中：是前后两观测站之间的距离；是前观测站短基线轴向与前后两观测站之间的基线方向的夹角。

将式（12）代入（14）后可得目标与远程观测站之间的径向距离的计算式：

（15）

式中：β以前后两观测站之间的基线方向为基准，目标相对于远程观测站的方位角。

另由余弦定律可解出远程观测站相对目标的方位角：

（16）

或利用正弦定理可解出：

（17）

3 远程观测站的测距误差

3.1 距离对相差的偏微分

远程观测站测距式（15）对相差的偏微分可改写为如下的形式：

（18）

其中程差对相差的微分是一个常数：

（19）

远程测距式（15）对程差的偏微分是：

（20）

3.2 近测距式对程差的偏微分

如设：

（21）

，即有：

近测距式对程差的偏微分：

（22）

其中：，

3.3 近观测方位角对程差的偏微分

设：

（23）

即有：

近观测方位角对程差的偏差微分是：

（24）

其中：

3.4 远程距离对近观测站短基线夹角的偏微分

测距式（15）对夹角的偏微分是：

（25）

3.5 后站距离对双站基线的偏微分

测距式（15）对双站间基线D的偏微分是：

（26）

3.6 远程测距的相对量误差

根据误差估计理论，对r，的相对测量误差是

（27）

式中：、、分别是相差、短基线与双站基线之间的夹角和两站间基线的均方根测量误差，且根据现有的工程测量能力，分别取：，，（km）

若不加说明，则分析计算时取远程观测站到目标的距离km。对进近探测站、取km，m，。

通过数据的计算与分析可以较清晰的说明增大双站何的距离有利于提高测距精度。仿真分析表明，短基线夹角对远程测距误差的影响较大，通过减小前站对目标的进近探测距离，增大前后的短基线长度都能显著提高远程测距精度。

4 结语

数学分析表明，远程测距精度是同时由前方观测站的短基线和前后双站之间的长基线决定的，于是，通过增加双站间的基线就能适当的压缩前分玩测站的短基線长度。由此就能实现前方近程观测站的小型化。

参考文献

[1] 杨勇.无人机对移动目标实时动态定位研究与实现[J].四川兵工学报，2014，3（35）：137-140.

[2] 胡海洋，李海林.基于图像匹配的无人机目标定位方法[J].舰船电子工程，2012，6（12）：49-51.

[3] 孙超，都基焱，段连飞.一种空间两点交会无人机定位方法[J].兵工自动化，2011，30（6）：35-36.

[4] 李道凯，原达，王晓静.基于MeanShift 方法和轨迹预测的目标跟踪算法[J].计算机工程与设计，2012，33（6）：2278-2279.

[5] 邵军.一种合作目标轨迹的处理方法[J].舰船科学技术，2012，8（8）：625-626.