基于单一行业的Markow itz模型实证分析——以新材料行业为例

王世臻

（安徽财经大学金融学院，安徽蚌埠233030）

基于单一行业的Markow itz模型实证分析
——以新材料行业为例

王世臻

（安徽财经大学金融学院，安徽蚌埠233030）

本文主要实证分析了Markowitz资产组合模型。在单一行业股票的历史数据风险溢价和协方差已知的前提下，并借助Excel solver和Matlab等计量分析工具，论文分别得到了“允许卖空”和“不允许卖空”情况下的最优投资组合。

Markowitz模型；最优投资组合；实证分析

一、相关理论

“不要把鸡蛋放在一个篮子”代表的分散化投资理念早在现代金融理论建立之前就已存在。然而，直到1952年, Harry Markowitz在《Journalof Finance》上发表的《Portfolio Selection》一文，才正式提出包含分散化原理的资产组合选择模型。在该文中，作者提出了“均值——方差”的分析方法和资产组合有效边界模型，并认为最优的资产组合遵循在预定收益率的前提下把风险降到最小或者在一定风险的前提下使期望收益率最大的法则。更进一步地，该文强调了资产组合选择应当在风险资产有效边界上选择最优投资组合。Markowitz资产组合理论不仅具有完美的理论性，而且在实际中也得到了有效的利用（包括我国的证券市场）。在文献[1]中，基于Markowitz资产组合理论，李善民和陈剑利等从沪深两股选取样本股票，对我国证券市场进行实证研究，结果表明该理论能够有效的分散风险。[1]而曹兴等为保证该模型预测的准确性，选择股本大的股票作为样本进行实证研究。[2]更进一步地，苏敬勤等在文献[3]中，以西部地域为背景，对涵盖西部各个行业的样本股进行实证分析。[3]但是，到目前为止，鲜有学者基于单一行业对Markowitz模型进行实证研究。本文以我国证券市场上新材料行业为基础，从一个全新的角度，对Markowitz模型进行了实证分析。

（一）Markow itz资产组合模型

1.Markowitz模型依据的假设。

（1）认为证券市场是有效的，资产的价格能够反映其内在价值。股价反映了全部的市场信息，投资者都知道各种资产的期望收益和标准差；（2）所有投资者都是理性的，都追求资产组合的方差最小；（3）各资产的收益之间存在相关性，可以用相关系数或协方差来表示；（4）投资者可以无限制地向银行借贷，且存贷利率一致；（5）交易是无摩擦的，即不存在交易费用以及税赋。

2.Markowitz模型的建立

根据上述假设，Markowitz模型建立了利用期望收益、风险度量的计算方法和有效边界理论，建立了用以选择最优资产组合的均值－方差模型：[4]

组合的期望风险溢价为：

整体的标准差为：

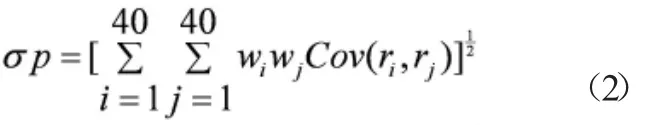
限制条件：

其中第i只股票的期望风险溢价为E(ri)，第i只股票的权重为，整体的期望风险溢价为E(rp)，标准差为σp，夏普比率为Sp，Cov(ri，rj)为两个证券之间的协方差。第一步，确定投资者面临的风险收益机会，得到最小方差边界（有效边界），进而确定最小方差组合。第二步，寻找报酬-波动性比率最高的资产配置线（夏普比率）。与有效边界相切，其切点就是最优风险组合。为了找到最小的方差组合，以(2)式为目标函数，为约束条件，运用Excelsolver求解可以得到最小的标准差和风险溢价。在边界上找到夏普比率最高的点，即有效边界上的最优的风险组合。把作为(4)式为目标函数，为约束条件运用Excelsolver求解可以得到最优风险组合的标准差。除此之外，本文根据资产是否能卖空，分别对允许卖空和不允许卖空两种进行情况讨论。

二、Markow itz资产组合选择模型实证分析

（一）样本股票的选取和来源

本文以新材料行业为背景，选取的研究时期为2011年1月至2014年12月,从A股中新材料行业中选取40只具有代表性的股票。并从RESSET数据库提取了方大集团等40只样本股票自2011年1月至2014年12月的日收盘价和月无风险收益率。

（二）样本的说明

本文选择2011年1月1日至2014年12月31日作为证券组合的样本时限,期间共计967个交易日。收益率计算所用的时间间距，一般可有年、月、周、日。由于本文主要在于分析股票的投资风险和收益，所以用代表中长期的投资收益率的月收益率。为了保持数据的连贯性，本文选择的

股票都是四年间没有停牌的。

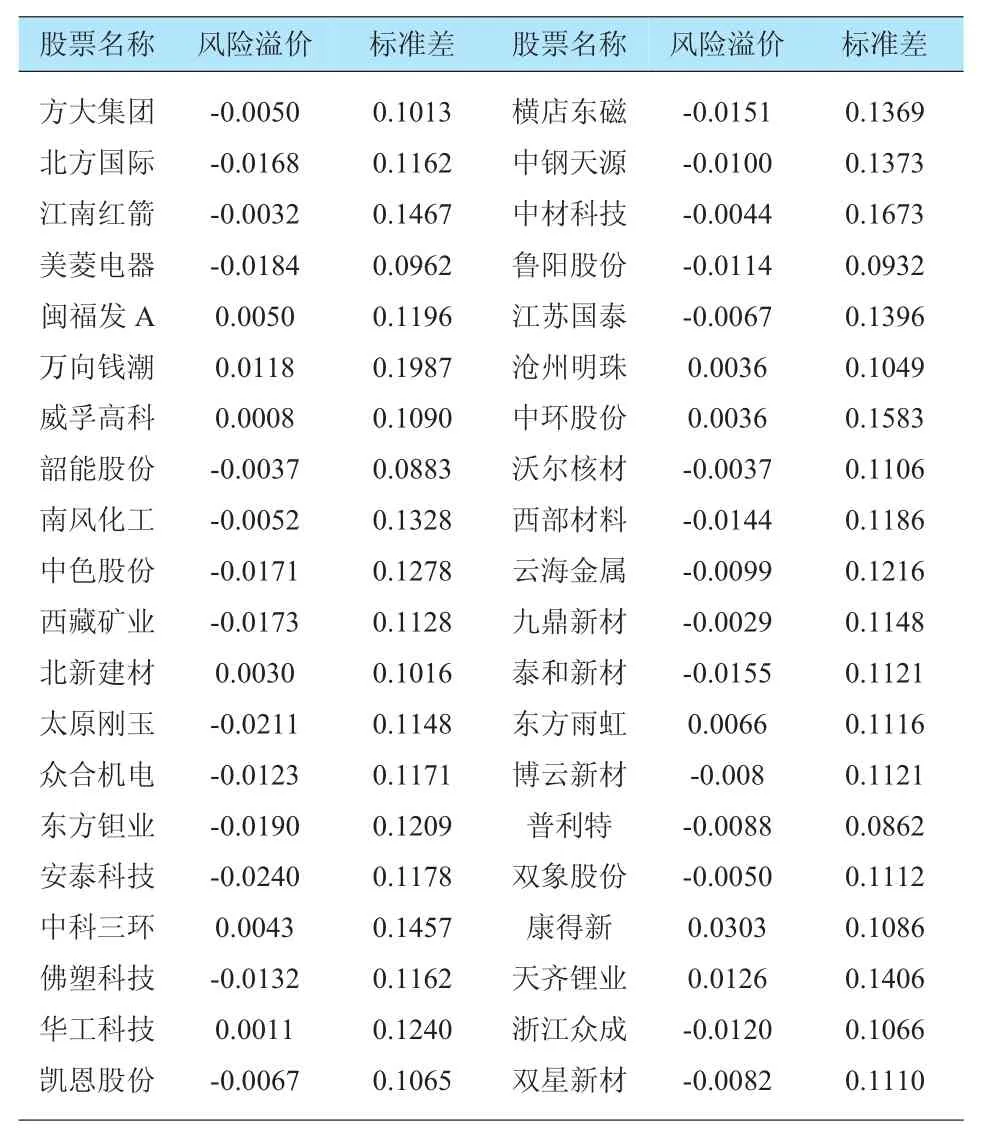
表1 样本股票风险溢价及标准差

（三）样本数据的处理

1.在RESSET金融数据库导出的每日收盘价的基础上，整理出月收益率，借助对应的月无风险收益率容易得到40只股票的风险溢价。（如表1）

2.通过计算，同时我们由2011年至2014年的月收益率可以得到这40只股票的标准差。（如表1）

3.为了找出最优风险组合，我们分允许卖空和不允许卖空两种情况进行讨论：

（1）允许进行卖空：

在有效边界的基础上，寻找边界上夏普比率最高的组合，即有效边界上的最优的风险组合。以(4)式为目标函数，以为约束条件，运用Excelsolver求解可以得到最优风险组合的标准差为0.0573，此时的风险溢价以及夏普比率分别为0.1009和1.7589，同时可以得到此时的风险组合。画出最优的资本配置线（如图1）。

（2）不允许卖空：

同理，在这种情况下，有了有效边界之后，寻找有效边界上的最优的风险组合。以(4)式为目标函数，以为约束条件运用Excel solver求解可以得到最优风险组合的标准差为0.1072，此时的风险溢价以及夏普比率分别为0. 0303和0.2825，同时可以得到此时的风险组合。画出最优的资本配置线（如图2）。

图1 卖空下的有效边界及最优配置线

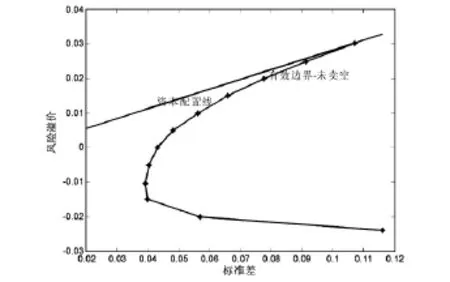
图2 未卖空下的有效边界及最优配置线

表2 两种情况下的标准差、风险溢价

4.结果分析

运用Markowitz均值-方差模型，采用历史数据得到的风险溢价、协方差，可以计算其最小方差集。借助有限边界和夏普比率得到最优资产投资组合。通过以上的运算结果表明，允许卖空机制下，最小标准差为0.0013，风险溢价为-0.0489；最优投资组合的最小标准差和风险溢价分别为0. 0573和0.1009。表明一味追求风险最小即标准差最小，所得到的风险收益甚至不及投资无风险收益资产，这样就表明投资活动是没有意义的，考虑交易等成本情况下收益更低。其次，最优投资组合较最小标准差组合而言，风险溢价增加的幅度显然比标准差增加的幅度大，单位收益承担的风险增加。但表明模型的优化配置的效果明显。由于交易机制的制约，在不允许卖空机制下，最小标准差为0.1163，风险溢价为-0.0240；最优投资组合的最小标准差和风险溢价分别为0.1072和0.0303。同样可以看出最优投资组合较最小方差组合，在风险和收益上均优于最小标准差组合。在不允许卖空机制下，受卖空机制约束，最优投资组合风险加大，收益降低。由“允许卖空”和“不允许卖空”情况下的夏普比率，我们可知，受不得卖空的交易机制影响，后者的夏普比率较低，单位收益承受的风险较大。

三、实证结论

实证分析结果表明，Markowitz资产组合理论在我国证券市场存在显著的应用价值。这表明该理论引导我国股民正确理性投资和促进证券市场健康稳定发展具有重要的意义。

（一）最优组合收益优于单个基础资产

表明虽然目前我国证券市场还不够规范，但资产组合理论已在我国股市还是具有一定的利用价值。通过表1和表2对比可知，在相同风险或者风险溢价条件下，有效组合的预期收益或风险较单个基础证券具有明显的优势。

（二）市场机制能在很大程度上影响优化投资组合

通过对允许卖空和不允许卖空两种机制比较分析得到，较为严格的市场机制一定程度上会使得投资者投资风险增加、投资收益减少。表明创新金融更加灵活的金融工具对于增加投资收益、激发投资热情大有裨益。

（三）Markow itz最优资产组合中基础证券分布集中

通过实证可知，在当前股市不允许卖空的机制下，最优组合内包括有三只股票，且主要集中在其中两种股票上。这种情况下，投资者可以把精力集中在最优组合内的少数股票上，不会把精力分散在各个单一的股票上，从而有效管理。

（四）在我国股票市场上运用Markow itz资产组合理论能得到比整个证券市场平均表现更好的证券组合

说明了市场并非有效的，对投资组合进行优化配置有达到击败市场的效果。但是，需要指出是，Markowitz理论是在一系列的假设下构建的，这些假设与真实的证券市场存在很大差异。所以，运用该理论进行真实的投资时，需要清醒地认识到理论本身所存在的缺陷以及模型与现实的差距。在实际投资过程中还应该结合实际的情况，进行适当的调整，避免不必要的损失。

[1]李善民，徐沛.Markowitz投资组合理论模型应用研究[J].经济科学，2000(1)：42～51.

[2]曹兴，彭耿.Markowitz投资组合理论在中国证券市场的应用[J].中南大学学报：社会科学版，2003(12)∶785～788.

[3]苏敬勤，陈东晓.Markowitz投资组合理论与实证研究[J].大连理工大学学报：社会科学版，2002(6)∶31～32.

[4]赵彦芬.修正的Markowitz投资组合模型在金融市场中的应用研究[D].大连：大连理工大学，2013(6)∶7～10.

［责任编辑：文筠］

F830.59

A

1005-913X（2015）12-0123-02

2015-09-22

王世臻(1992-)，男，安徽安庆人，本科学生，研究方向：金融市场。