基于一类超图的理想存取结构

李志慧，张娜娜

（陕西师范大学数学与信息科学学院，西安710119）

·安全技术·

基于一类超图的理想存取结构

李志慧，张娜娜

（陕西师范大学数学与信息科学学院，西安710119）

具有n个参与者形成的存取结构集合与具有n个顶点的超图集合之间存在一一对应关系。定义一类超图，即r-一致完全k分超图，运用向量空间构造法证明该类超图对应的存取结构是理想的，进而利用组合数学知识计算出该类超图存取结构的数目。在有限域F7上给出参与者人数为4，5，6的所有r-一致完全k分超图存取结构。验证结果表明，相比（r，n）门限存取结构和完全k分图存取结构，该类理想的超图存取结构更为一般化，应用更为广泛。

超图；完全k分超图；存取结构；理想存取结构；向量空间构造

1 概述

秘密共享在提供重要数据的安全性、防止秘密信息丢失等方面有着重要的作用，它被广泛地应用于通信密钥管理、电子拍卖、电子选举等实践中。设n是一个正整数，令参与者集合P=｛P1，P2，…，Pn｝，在一个秘密共享体制中，对于主密钥s，参与者集合P中只有那些事先授权的子集中的参与者，利用他们所持有的秘密份额才能恢复秘密，这些子集组成的集合Γ称为存取结构，其中的子集叫授权子集。如果一个授权子集的任意真子集均不能恢复秘密，称这个授权子集为极小授权子集，由所有极小授权子集组成的集合称为极小存取结构。

一个秘密共享体制称作完善的，如果参与者中的非授权子集不能得到关于密钥的任何信息。文献［1］利用熵的概念，证明了在任何完善门限秘密共享方案中，参与者得到的共享一定至少和密钥一样长，随后，文献［2］把这个结果推广到任何完善秘密共享方案中。这意味着在完善秘密共享方案中有数据扩散。出于安全性考虑，主密钥空间通常取得较大，以防止攻击者的穷搜索。但是另一方面，数据扩散增加了子密钥的长度，给子密钥的保管带来了困难，因此，希望找到没有数据扩散的完善秘密共享方案。针对这种想法，文献［3］引进了理想秘密共享体制的概念。对于任意一个存取结构Γ来说，都存在一个实现该结构的秘密共享方案，当存在一个理想的秘密共享方案实现了存取结构Γ，即存取结构Γ是理想的。

Sham ir［4］和B lak ley［5］于1979年分别独立地提出了秘密共享的概念，并给出了Sham ir（k，n）门限秘密共享方案。这类方案对应的门限存取结构是理想的，但结构比较单一。文献［6-8］研究了图存取结构的秘密共享方案，证明了完全k分图（也称作完全多划分图）所对应的存取结构均是理想的，但是这类方案的存取结构的秩只能为2。

本文对完全k分图的定义给予推广，提出r-一致完全k分超图的概念，证明了该类超图对应的存取结构，进而计算这类理想超图存取结构的数目。

2 预备知识

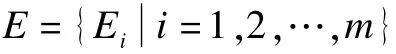
定义2 在超图H（V，E）中，设Ei，Ej是它的任意两个超边，若满足Ei⊆Ej，则必有Ei=Ej，称H（V，E）为一个简单超图［9］。秩为r的简单一致超图称为r-一致超图。

注1 秩为2的超图，即将超图H（V，E）记为G（V，E）。

定义3 在超图H（V，E）中，如果对任意2个顶点u，v∈V都存在从u到v的一条超径，则该超图被称作是连通超图［10］，即存在一个超边序列Ei1，Ei2，…，Eis使得：

其中，j=1，2，…，s-1。

定义4 在图G（V，E）中，若每对互异顶点恰有一条边相连接，则称此图为完全图［11］。阶为n的完全图记为Kn。

定义5 在超图H（V，E）中，若每r个互异顶点恰有一条边相连接，则称此超图为r-一致完全超图，阶为n的r-一致完全超图记为。

定义6 在图G（V，E）中［11］，若V=V1∪V2，V1∩V2=φ，且Vi中任意2个顶点都不相连接（i= 1，2），则称H（V，E）为二分图；若V1中每个顶点都与V2中的每个顶点相连接，则称H（V，E）为完全二分图，记为Km，n，其中，。

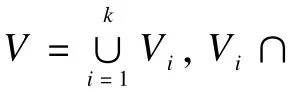
注2 当k=n时，r-一致完全k分超图可以看作r-一致完全超图。

例1 在超图H（V，E）中，令V=｛1，2，3，4，5｝，E=｛123，124，125，134，135，234，235｝。令V1=｛1｝，V2=｛2｝，V3=｛3｝，V4=｛4，5｝，则这时该超图H（V，E）可看作一个3-一致完全4分超图。

定义9 超图H（V，E）与H′（V′，E′）称为同构的［9］，当且仅当存在一一映射f：V→V′和g：E→E′。且这2个映射保持关联关系，即：g（e）=f（v1）f（v2）…f（vt），∀e=v1v2…vt∈E，vi∈V，i=1，2，…，t。

引理1 如果2个超图同构，那么这2个超图的顶点数相同，超边数相同，秩相同，且顶点在超边中出现的次数相同［12］。

在秘密共享中，极小存取结构Γ0，Γ0⊆2P，可以表示为一个超图H（P，Γ0），其中每个参与者表示这个超图H（P，Γ0）的一个顶点，每个极小授权子集表示这个超图H（P，Γ0）的一个超边。显然，H（P，Γ0）是一个简单超图。将极小存取结构Γ0看作超图H（V，E）中的超边集E时，这个极小存取结构Γ0就为超图存取结构。

注3 （r，n）门限存取结构是r-一致完全k分超图存取结构的特殊情况，设参与者人数为n，可看作超图的n个顶点，只需把顶点n划分，那么对应的r-一致完全k分超图就是（r，n）门限存取结构。

定义10 如果2个参与者u和v在存取结构中的作用是一样的，即对任意包含u但不包含v的授权子集W和任意包含v但不包含u的授权子集V，W′=（W｛u｝）∪｛v｝和V′=（V｛v｝）∪｛u｝都是授权子集，那么这2个参与者称为等价的。

由定义8知，r-一致完全k分超图中的任一个顶点集合Vi（i=1，2，…，k）中的顶点都是等价的。

引理2 设G（V，E）是一个完全k分图，则存在一个理想秘密共享方案实现了参与者集合V上的极小存取结构E［13］。

引理3 设不定方程组［14］：

令B（n，k）为式（1）的正整数解的个数，则有：

（1）B（n，1）=B（n，n-1）=B（n，n）=1；

（3）当k＞n时，B（n，k）=0；

（4）B（n，k）=B（n-1，k-1）+B（n-k，k），n，k∈N；

（5）B（n+k，k）=B（n，1）+B（n，2）+…+B（n，k），n，k∈N。

3 理想存取结构

设Γ是一个存取结构，（Fp）d是Fp上所有的d元组组成的向量空间，其中，p是素数，d≥2。假定存在函数：

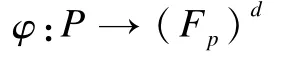
满足性质：

若找到满足式（2）的向量的集合，则可建立实现存取结构Γ的理想秘密共享方案。这个方案被称为基于向量空间秘密共享方案［13］。

定理1 设H（V，E）是一个r-一致完全k分超图（2≤r≤k），则存在一个理想秘密共享方案实现了参与者集合V上的极小存取结构E。

证明：易知H（V，E）的秩为r，设参与者人数为n，令V1，V2，…，Vk是顶点集合V的划分，x1，x2，…，xk是有限域Fp中互不相同的非零元素，其中，p＞k，令d=r。设，其中，i=1，2，…，k，l1+ l2+…+lk=n。为了简便起见，不妨设V1=｛v1，v2，…，vl1｝，…，Vk=｛vl1+…+lk-1+1，…，vl1+…+lk｝，对于每个参与者v∈V，构造φ函数如下：

其中，vi1，vi2，…，vir表示顶点集V中任意r个不同的顶点，当vi1，vi2，…，vir是一个极小授权子集时，由该类超图存取结构以及φ函数定义代入式（3）。式（3）对于mod p运算有且仅有一个解，且各分量都是非零的；对任何非授权子集代入相应的φ函数，此时式（3）的系数矩阵与其增广矩阵的秩不等，故对于mod p运算无解，从而得不到主密钥的任何信息，显然满足式（2）。根据基于向量空间秘密共享方案是理想秘密共享方案知，r-一致完全k分超图存取结构是理想的存取结构。

注4 当r=2时，就是完全k分图，由引理2知存在一个理想秘密共享方案实现了该图存取结构。

例2（接例1） 令k=4，r=3，在有限域F7上定义函数φ如下：

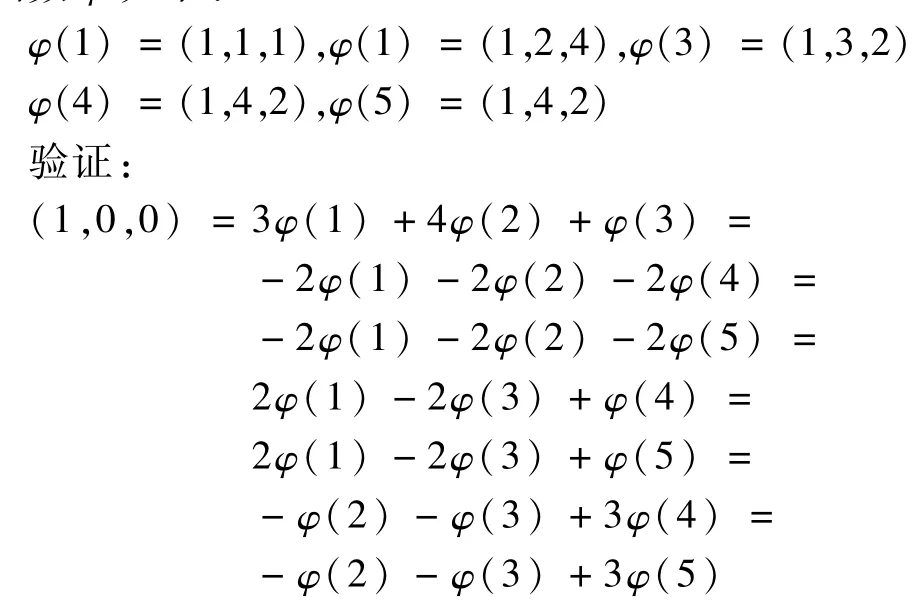
如果B是最大非授权子集，只需证明（1，0，0）∉〈φ（pi）：pi∈B〉。一共有6个这样的子集B需要考虑：｛12｝，｛13｝，｛23｝，｛145｝，｛245｝，｛345｝。对每种情况需建立一个特定的线性方程组，易知这些方程组均无解。例如，假设（1，0，0）=xφ（1）+yφ（2），其中，x，y∈F7，容易看出，此方程组无解。其余情况类似验证。所以该存取结构是理想的。

定理2 设H（V，E）是一个含有n个顶点的超图，将顶点集V划分成k个非空子集的并，则这种划分共有B（n，k）种。

证明：由于n个顶点与k个非空集合均是无区别，因此可以将这个顶点集的划分问题可以看成式（1）的整数解的个数问题，从而顶点集合的这种划分有B（n，k）种。

例3 在超图H（V，E）中，令n（H）=9，k=5，那么这种情况下顶点集V的5划分的个数为：B（9，5）=B（4+5，5）=B（4，1）+B（4，2）+ B（4，3）+B（4，4）+B（4，5）=1+2+1+1+0=5。

定理3 设H（V，E）是一个含有n个顶点且秩为r的超图，则r-一致完全k分超图存取结构有（k-1）B（n，k）个，其中，2≤r≤k≤n。

证明：由r-一致完全k分超图的定义知：2≤r≤k，2≤k≤n。当k=2时，由定理2知顶点集V的划分有B（n，2）种，此时r只能有一种取值，即r=2，故对应的r-一致完全k分超图有1·B（n，2）= B（n，2）个；当k=3时，顶点集V的划分有B（n，3）种，此时r有2种可能取值，即r=2，3，故对应的r-一致完全k分超图有2·B（n，2）=2B（n，2）个；依次类推，当k=n时，顶点集V的划分有B（n，n）种，此时r的n-1个可能取值为2，3，…，n，故对应的r-一致完全k分超图有（n-1）·B（n，n）个。故顶点数为n时，所对应的r-一致完全k分超图有B（n，2）+2B（n，3）+…+（n-1）B（n，n）=B（n，k）个，故这类超图存取结构有B（n，k）个。

例4 设H（V，E）是一个含有6个顶点的超图，则所对应的r-一致完全k分超图存取结构的个数为∑6

k=2（k-1）B（6，k）=B（6，2）+2B（6，3）+ 3B（6，4）+4B（6，3）+5B（6，6）=24。

4 实例验证

根据定义8中r-一致完全k分超图的概念，给出了有限域F7上顶点数为4，5，6的所有r-一致完全k分超图（2≤r≤k）及相对应的理想存取结构，如表1所示。

表1 F7上顶点数为4，5，6的r-一致完全k分超图存取结构（2＜r≤k≤n）

根据引理1及定义9，在表1中给出了所有互不同构的r-一致完全k分超图，即表中这些理想存取结构是互不同构的。在表1中，当n=4，5，6时，相对应的这类理想存取结构的数目分别为7，13，24。分析表明，当顶点数n增大时，这类理想存取结构的数目明显增多。从表1中看到，这类新的理想存取结构比较丰富，且理想的（r，n）门限存取结构和完全k分图对应的理想的存取结构均是这类超图存取结构的特殊情况。

5 结束语

本文定义了一类特殊超图-r，即一致完全k分超图，利用向量空间构造法证明了基于该类超图的存取结构是理想的，给出了这类超图存取结构的计数，本文构造的这类特殊超图存取结构在结构上是丰富的。相比理想的（r，n）门限存取结构和完全k分图对应的理想的存取结构，r-一致完全k分超图对应的理想存取结构更为一般化，不局限于一个（r，n）门限存取结构中极小授权子集的个数为以及一个完全k分图存取结构中秩一定为2的情况。在实际应用中，由于这类超图存取结构还具有向量空间秘密共享方案的（+，+）同态性质［15］，且结构丰富，因此这类超图存取结构可用于替代许多电子协议中曾使用的存取结构，能克服这些方案存在的不足。如在文献［16-17］的电子投票协议中计算选票时，唱票人所在的存取结构不具有灵活性或存取结构是非完善的，均可用这类存取结构替代，以提高方案的效率及使用时的灵活性。

［1］ Karnin E D，Greene J W，Hellman M E.On Secret Sharing System s［J］.IEEE Transactions on Information Theory，1983，29（1）：35-41.

［2］ Capocelli R M，Santis A D，Gargano L.On the Size of Shares for Secret Sharing Schemes［J］.Journal of Cryptology，1993，6（3）：157-167.

［3］ Brickell E F，Davenport D M.On the Classification of Ideal Secret Sharing Schemes［J］.Journal of Cryptology，1991，4（1）：123-134.

［4］ Sham ir A.How to Share a Secret［J］.Communications of the ACM，1979，22（11）：612-613.

［5］ Blahley G.Safeguarding Cryptographic Keys［C］// Proceedings of National Computer Conference.New York，USA：ACM Press，1979：313-317.

［6］ Hsu Changfang，Qi Cheng，Tang Xueming，et al.An Ideal Multi-secret Sharing Scheme Based on MSP［J］. International Journal of Information Sciences，2011，181（7）：1403-1409.

［7］ Jackson W，M artin K M.Pefect Secret Sharing Schemes on Five Participants［J］.Journal of Designs，Codes and Cryptography，1996，9（3）：267-286.

［8］ 刘木兰，张志芳.密钥共享体制和安全多方计算［M］.北京：电子工业出版社，2008.

［9］ 法C.贝尔热.超图-有限集的组合学［M］.卜月华，张克民，译.南京：东南大学出版社，2002.

［10］ Crescenzo G D，Galdi C.Hypergraph Decomposition and Secret Sharing［J］.Discrete Applied Mathematics，2009，157（5）：928-946.

［11］ 王树禾.图论［M］.北京：科学出版社，2004.

［12］ 杨丽杰，李志慧，李 婧.一类超图存取结构的秘密共享方案的信息率［J］.计算机应用研究，2013，30（7）：2115-2119.

［13］ Stinson D R.密码学原理与实践［M］.3版.冯登国，译.北京：电子工业出版社，2009.

［14］ 潘永亮，徐俊明.组合数学［M］.北京：科学出版社，2006.

［15］ 张倩倩，李志慧，雷 娟.基于向量空间上的无分发者的秘密共享方案［J］.计算机应用研究，2011，28（6）：2230-2232.

［16］ Benaloh J.Secret Sharing Homomorphisms：Keeping Shares of a Secret Secret［C］//Proceedings of CRYPTO'86. Berlin，Germany：Springer，1987：251-260.

［17］ Iftene S.General Secret Sharing Based on the Chinese Remainder Theorem with Applications in E-Voting［J］. Elctronic Notes in Theoretical Computer Science，2007，186：67-84.

编辑索书志

Ideal Access Structure Based on a Type of Hypergraph

LI Zhihui，ZHANG Nana
（College of Mathematics and Information Science，Shaanxi Normal University，Xi'an 710119，China）

There exists a one-to-one correspondence between the set of access structures with n participants and that of hypergraphs with nvertices.This paper proposes a type of hypergraph，i.e.，r-uniform hypergraphs with complete kpartition.It proves that the type of hypergraph access structures is ideal by using vector space construction.The paper gives the number of this type of ideal hypergraph access structures using combinatorial mathematics，and gives all the ideal access structures w ith the number of participants（or vertices）4，5，6 over a finite field F7based on the r-uniform hypergraph with complete k-partition.Test results show that，com pared with（r，n）threshold access structures and complete k-partition graph access structures，the proposed ideal access structures are more vivid，and can be extensively applied in practice.

hypergraph；complete k-partition hypergraph；access structure；ideal access structure；vector space construction

李志慧，张娜娜.基于一类超图的理想存取结构［J］.计算机工程，2015，41（11）：165-169.

英文引用格式：Li Zhihui，Zhang Nana.Ideal Access Structure Based on a Type of Hypergraph［J］.Computer Engineering，2015，41（11）：165-169.

1000-3428（2015）11-0165-05

A

TP391

10.3969/j.issn.1000-3428.2015.11.029

国家自然科学基金资助项目（61373150）；陕西省科学技术研究发展计划工业攻关基金资助项目（2013K 0611）。

李志慧（1966-），女，教授、博士，主研方向：有限域，密码学；张娜娜，硕士研究生。

2014-10-24

2014-12-03 E-m ail：lizhihui@snnu.edu.cn