fGn模型在结肠癌基因表达数据集去噪中的应用
艾玲梅,李 科,马 苗
(陕西师范大学计算机科学学院,西安710119)
fGn模型在结肠癌基因表达数据集去噪中的应用
艾玲梅,李 科,马 苗
(陕西师范大学计算机科学学院,西安710119)
基因表达数据集获取过程中容易掺杂噪声成分,噪声会干扰数据的正确表达从而影响其后期的分析与研究。基于中值计算法估计噪声标准差的经验模态分解(EMD)去噪存在一定的不足,从而影响去噪效果。分数阶高斯噪声(fGn)模型可提供EMD下较为准确的噪声标准差估计方法,在该模型下去噪可减少白色及有色噪声,进而增强去噪效果。因此在中值计算EMD去噪基础上,提出一种基于fGn模型的去噪方案,并对结肠癌基因表达数据集做去噪分析。实验结果表明,相比中值计算EMD去噪方法,改进方法的信噪比、噪声抑制比、t检验等值具有一定的优势,可作为基因表达数据集去噪的一种参考方案。
基因表达数据集;经验模态分解去噪;噪声标准差;分数阶高斯噪声;结肠癌
1 概述
基因表达数据集是由生物芯片经后期计算机辅助技术的加工处理而获得,其最大的优势在于能够同时反映成千上万个基因在样本中的存在情况[1-3],但是数据集的制备过程容易受电子、荧光等外在干扰的影响形成噪声,噪声的存在使基因无法准确反映其在样本中的表达值,进而影响进一步的分析,因此,数据集去噪成为数据预处理的一项重要任务[4]。
目前基因表达数据集去噪的文献相对较少,常用方法是小波分析去噪。该方法计算简便且在信号的时域和频域都具有较好的局部分析能力,但是小波去噪中母函数和分解层数的确定较为困难,通常将以往经验作为选择依据,加之小波去噪对母函数及分解层数的选择较为敏感,因此,小波分析用于信号去噪时也存在一定缺陷。相比之下,经验模态分解(Empirical Mode Decomposition,EMD)在信号分解时无需考虑母函数及分解层数,可以根据信号特点自适应地迭代分解,除此之外EMD还具有较好的近似正交性、完备性等诸多优点,可作为去噪研究的基本工具[5]。文献[5]中值计算EMD去噪方案使用中值计算法估计噪声标准差具有一定的局限性,去噪效果不甚理想,针对该问题尝试做进一步分析与改进。文献[6]中,在分数阶高斯噪声(fractional Gaussian noise,fGn)模型下,有一种较为合理的噪声标准差计算方式,可以较准确地反映噪声在EMD下的分布。由于该模型是离散高斯白噪声的一种广义化模型,涵盖有白色及有色噪声,因此在该模型下去噪可以减少白色及有色噪声成分,进一步增强去噪效果[6-7]。因此本文在中值计算EMD去噪基础上,结合fGn模型下改进的噪声标准差计算方式,对结肠癌基因表达数据集做去噪处理,以期提升去噪效果。
2 EMD去噪
经验模态分解(EMD)[8]的实质是将信号分解为有限个本征模态函数(Intrinsic Mode Function,IMF)分量和一个余项:
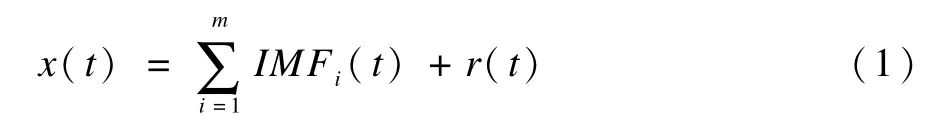
EMD去噪[5]需要首先对带噪信号EMD分解求得各个IM F分量和余项;其次对带噪IM F分量做阈值去噪处理;最后将去噪后的IMF分量和剩余IMF分量及余项求和重构即完成信号去噪。该过程第2个环节可借助归一化自相关函数[5]判断哪些IM F分量需要去噪。
图1(a)仿真序列归一化自相关函数在不同时间差内均有数值相对应,图1(b)的仿真噪声序列归一化自相关函数除了在零点处有最高值外,整个时间差内取值均在零处徘徊。因此求取IMF分量的归一化自相关函数,根据各个函数的分布特点可大致判断哪些IMF分量中含有噪声及强度,又因IMF分量中噪声成分逐级呈递减趋势,因此可判断IM F分量中噪声和信号的分离点,分离点之前的IMF分量需要去噪,之后的IM F分量中信号的有用成分较多要保留[5]。
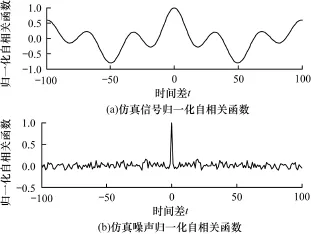
图1 仿真序列和噪声归一化自相关函数
3 噪声标准差估计
3.1 中值计算法
EMD去噪实质是对IM F分量做阈值去噪,阈值的选择极其重要,阈值计算如下[9]:
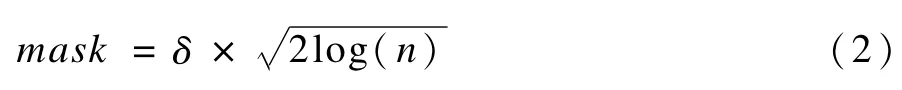
其中,mask表示阈值;n表示信号长度;δ表示信号噪声标准差,对于既定信号而言噪声标准差是阈值计算的唯一参量,因此,噪声标准差是决定阈值去噪的关键。文献[5]中值计算EMD去噪使用中值计算法估计噪声标准差:

其中,x表示任意带有噪声的信号序列;C为固定值,一般取0.674 5;Median是中值函数[9-10]。中值计算法[11]以其较好的鲁棒性适用于大部分信号,是计算噪声标准差较为常用的方式。
3.2 fGn模型下计算方法
文献[6]中,在分数阶高斯噪声(fGn)模型下,带噪信号EMD分解后各个IMF分量间噪声方差的代数关系可表示如下:

其中,H指信号Hurst值[6,12-14];ρH通过式(5)求出;V(K′)为第K′阶IMF分量的方差;V(K)指第K阶IMF分量的方差(K′>K≥2),而IMF分量的噪声标准差只需对噪声方差做开方即可。
4 fGn模型下改进的EM D去噪算法
中值计算EMD去噪方案对信号EMD分解得到各阶IM F分量并计算其归一化自相关函数,根据信号与噪声归一化自相关函数分布的不同找出IM F分量中噪声和信号的分界点M,位于M阶之前的IMF分量阈值去噪处理,位于M阶之后的IMF分量中有用成分较多保持不变,最后将去噪后的IMF分量与剩余IMF分量及余项求和完成信号重构即可[5]。整个去噪过程的关键在于阈值的确定,而阈值中有个重要变量,即噪声标准差,可见噪声标准差估计是个不可忽视的环节。
中值计算EMD去噪[5]采用中值法计算噪声标准差,虽然具有广泛的适用性,但是缺乏针对性。首先中值计算主要适用于小波域下计算噪声标准差,而本文的去噪是以EMD为基础的;其次中值计算法在进一步的研究中发现,噪声偏小时中值计算噪声标准差的准确度会下降[11]。因此,本文针对该问题联合fGn模型下改进的噪声标准差计算方法,从而改善中值计算EMD去噪。
fGn模型下噪声标准差的计算中,通过观察IMF分量的归一化自相关函数的分布找出噪声与信号的外分界点M,而在前M阶IMF分量中继续根据IMF分量噪声的强弱找出内分界点M′,因为前M′阶IMF分量里噪声成分较重,所以可以采用式(3)中值计算,而M′到M阶IM F分量噪声成分相对较少,则应该采用式(4)计算。
从式(4)可以看出信号EMD分解后各阶IMF分量间噪声方差的关系,V(K)可作为初始方差,V(K′)是第K′阶IMF分量的方差(K′>K),H代表信号的Hurst值[6-7]。为了更加准确估计IM F分量的噪声标准差,H将表示各阶IMF分量的Hurst值,然而IM F分量的Hurst值相比于整体信号的Hurst值有偏小的趋势,因而尝试将初始方差增大。信号EMD分解后IM F分量的阶数越小,其分量中带有的噪声成分越大,噪声标准差也会越大,文献[6]中初始方差定在第二阶IMF分量,因此将式(4)稍加修改如下:

其中,H指第j阶(j>M′)IM F分量Hurst值;ρH值可以通过式(5)求出;M′指IMF分量里的内分界点;V(j)指第j阶IM F分量的噪声方差;V(2)指第二阶IM F分量的噪声方差。针对本研究基因信号的去噪处理,阈值计算式(2)稍作修改如下:
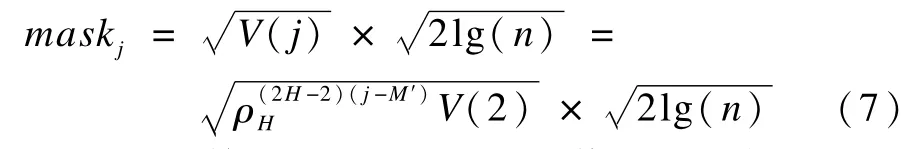
其中,maskj为第j阶IM F分量阈值;H指该分量的Hurst值;ρH值可以通过式(5)计算;M′为IMF分量的内分界点;V(2)为第二阶IMF分量的噪声方差;n为IMF分量长度。
阈值确定后只需要将IMF分量做软阈值处理即可,软阈值函数[15]如下:
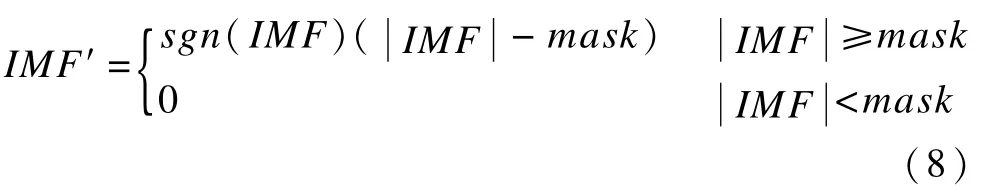
其中,mask为对应IM F分量的去噪阈值;去噪后的IMF分量与其余的IMF分量及余项求和即完成去噪。
综上所述,本研究基于fGn模型的EMD去噪算法如下:
(1)基因样本信号做EMD处理得到各个IMF分量;
(2)根据各个IMF分量的归一化自相关函数的分布特点找出噪声和信号的外分界点M;
(3)在前M阶IMF分量中根据噪声强度进一步找出内分界点M′;
(4)1到M′阶IMF分量的噪声标准差采用式(3)计算,M′+1到M阶IMF分量的噪声标准差采用式(6)做算术开方即可;
(5)根据式(7)计算M阶之前的各个IMF分量的去噪阈值并且按照式(8)进行去噪处理;
(6)去噪处理后的IM F分量与剩余IMF分量及余项求和重构信号。
5 实验结果与分析
5.1 仿真实验
为了验证本文方法在减少白色及有色噪声上的有效性,首先进行仿真实验,该实验的运行平台是M atlab(R2008b)。实验在原始仿真信号x=sin(2× pi×30×t)+cos(2×pi×10×t)中分别加入仿真白噪声[5]和有色噪声(Hurst值不等于0.5时的分数阶高斯噪声),在中值计算EMD去噪和本文方法下做去噪处理,量化指标使用信噪比(Signal Noise Ratio,SNR)sSNR和均方根误差(Root M ean Squared Error,RMSE)rRMSE定义如下[16]:
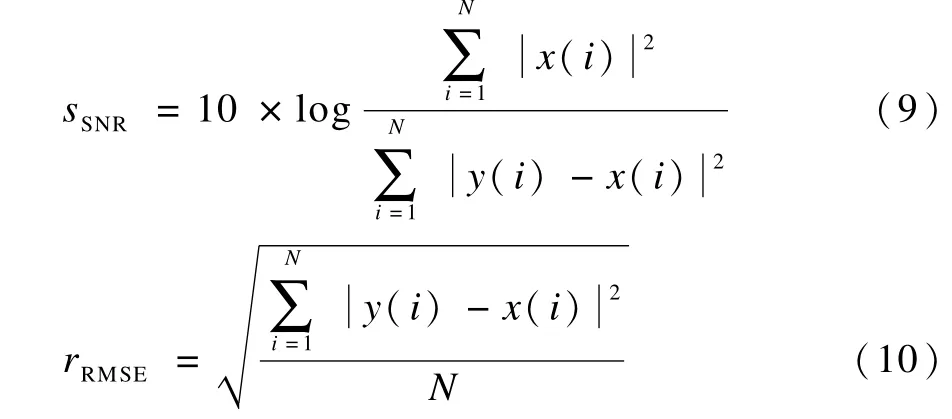
其中,N为信号长度;x为初始信号;y为去噪后的信号。根据如上定义可以看出,去噪后信号中含有的噪声越小,SNR越大,去噪效果越好,去噪后信号与初始信号越接近,RMSE越小,去噪效果越好。
带噪信号为仿真信号x=sin(2×pi×30×t)+ cos(2×pi×10×t)[5]加入仿真白噪声,中值计算EMD去噪与本文方法去噪效果如图2所示。
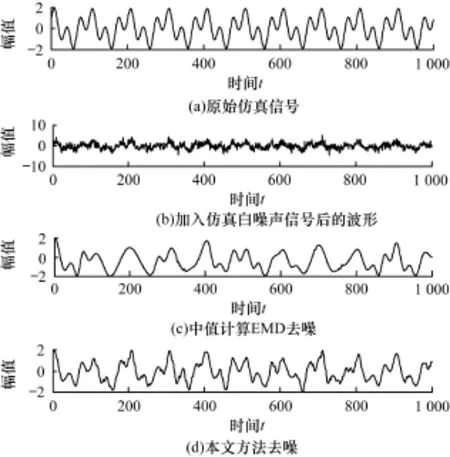
图2 带有仿真白噪声的信号去噪效果对比
从图2(c)和图2(d)可以看出,由于中值计算EMD去噪方法存在的不足,导致去噪后信号虽然光滑却丢失原始仿真信号诸多细节信息,而使用本文去噪方法可以较好恢复原始仿真信号,去噪效果得到了很大提升。针对有色噪声的去噪实验,需要在信号中添加有色噪声,仿真信号x=sin(2×pi× 30×t)+cos(2×pi×10×t)[5]加入Hurst=0.7的fGn即可仿真为带有有色噪声的信号[7]。从表1白色及有色噪声去噪效果量化对比可以看出,本文去噪方法的SNR和RMSE值明显优于中值计算EMD去噪。
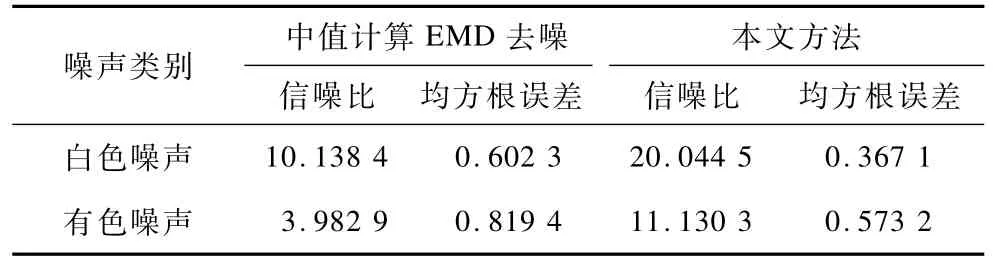
表1 白色及有色噪声去噪效果量化对比
5.2 基因表达谱信号去噪
本文所用数据来自于结肠癌基因表达数据集[17],其中含正常和病变样本共62例,每例样本均包含2 000个基因。该数据集模型化后为一个62行2 000列的矩阵X,矩阵中的每一个值Xij(i=1,2,…,62,j=1,2,…,2 000)表示基因j在样本i中的表达值。该数据集在去噪处理之前需要进行标准化处理,以消除数据量纲间的差异[18],矩阵中的数据Xik=(Xik-μk)/σk,其中,μk表示第k列的均值;σk表示第k列的标准差。
本数据集由于缺乏原始不带噪声的信号,所以去噪效果的量化指标不再选用SNR和RMSE,而是采用噪声抑制比(Noise Rejection Ratio,NRR),定义如下:
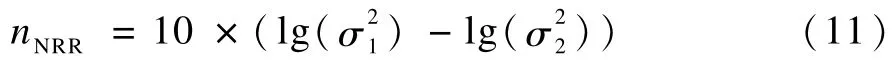
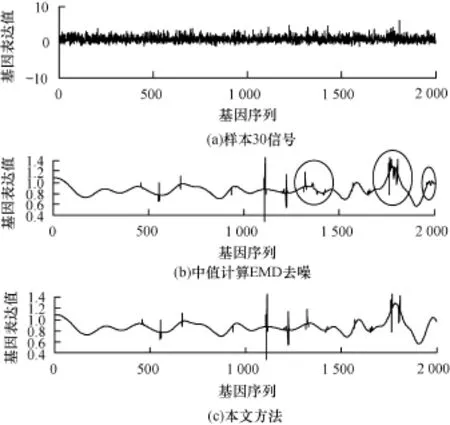
图3 样本30去噪效果对比
本文去噪方法相比于中值计算EMD去噪的改进之处在于噪声标准差的估计。表2对噪声标准差的2种算法进行了分析,由于本实验基因信号的长度为2 000,因此耗时是在该长度序列下测试的大约运行时间。可以看出,基于fGn模型的算法步骤多一个环节,但本文方法只对需要计算噪声标准差的IM F分量中的一部分采用该算法,另外从2种方法计算噪声标准差的耗时上可以看出其用时差异较小,综合来看本文方法在提升基因表达数据集去噪效果的同时并没有明显增加算法的计算复杂度。

表2 噪声标准差算法分析
6 结束语
针对中值计算噪声标准差在EMD去噪中存在一定局限性的问题,本文提出结合分数阶高斯噪声(fGn)模型计算噪声标准差的EMD去噪方案。该方案以fGn模型为基础,基因信号EMD分解后得到各阶IMF分量,以归一化自相关函数为判断依据,不同类的IMF分量采用对应的噪声标准差计算方式,最后做阈值去噪处理。fGn模型去噪不仅可以提升阈值计算的准确性,而且可以减少有色噪声。仿真实验及结肠癌基因表达数据集去噪结果表明,信噪比、噪声抑制比、t检验等指标整体优于中值计算EMD去噪,进一步提升了去噪效果。相关研究显示,基因信号中的噪声较重且来源较复杂,如何根据噪声源有针对性地去除噪声将成为未来的研究方向。
[1] 吴海霞,冯 伟,冉 维.时滞基因调控网络的全局渐进稳定性分析[J].计算机应用研究,2014,31(1):59-62.
[2] 刘庆山,陈小玉,庄述娟.基因表达谱芯片技术进展及其在中药网络药理学研究中的应用[J].时珍国医国药,2014,25(2):502-504.
[3] 阚海俊,唐 俊,苏亮亮.一种基于邻域不定性信息和记分准则相结合的肿瘤特征基因提取方法[J].安徽大学学报:自然科学版,2014,38(1):79-83.
[4] 许忠能.生物信息学[M].北京:清华大学出版社,2008.
[5] 王 婷.EMD算法研究及其在信号去噪中的应用[D].哈尔滨:哈尔滨工程大学,2010.
[6] Flandrin P,Rilling G,Gonçalves P.EMD Equivalent Filter Banks,from Interpretation to Applications[J]. World Scientific,2005,(12):67-87.
[7] Gan Yu,Sui Lifen,Wu Jiangfei,et al.An EMD Threshold De-noising Method for Inertial Sensors[J]. Measurement,2014,49:34-41.
[8] Huang N E,Shen Z,Long S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proceedings of the Royal Society of London,Series A:Mathematical,Physical and Engineering Science,1998,454(1971):903-995.
[9] Donoho D L,Johnstone J M.Ideal Spatial Adaptation by Wavelet Shrinkage[J].Biometrika,1994,81(3):425-455.
[10] Donoho D L,Johnstone I M.Adapting to Unknown Smoothness via Wavelet Shrinkage[J].Journal of the American Statistical Association,1995,90(432):1200-1224.
[11] 李淑霞,王汝霖,李春梅,等.基于噪声方差估计的小波阈值图像去噪新方法[J].计算机应用研究,2007,24(1):220-221.
[12] 徐 凌,刘嘉焜,李 亮.自相似网络流量Hurst指数估计算法[J].科学技术与工程,2013,13(20):5848-5854.
[13] 刘付斌,高相铭.基于EEMD与DFA的Hurst指数估计[J].测控技术,2013,32(10):98-101.
[14] 冶晓隆,兰巨龙,黄万伟.基于FRFT自相似参数估计的异常流量检测方法[J].计算机应用研究,2013,30(6):1783-1785.
[15] Donoho D L.De-noising by Soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.
[16] 陶 珂,朱建军.小波去噪质量评价方法的对比研究[J].大地测量与地球动力学,2012,32(2):128-133.
[17] Alon U,Barkai N,Notterman D A,et al.Broad Patterns of Gene Expression Revealed by Clustering Analysis of Tumor and Normal Colon Tissues Probed by Oligonucleotide Arrays[J].Proceedings of the National Academy of Sciences,1999,96(12):6745-6750.
[18] 张玉春,郝平波,王明宇,等.结肠癌基因表达谱的分类检测问题研究[J].计算机工程与应用,2011,47(17):244-248.
[19] 刘云鹏,律方成,李成榕,等.基于数学形态滤波器抑制局部放电窄带周期性干扰的研究[J].中国电机工程学报,2004,24(3):169-173.
编辑顾逸斐
Application of fGn Model in Colon Cancer Gene Expression Dataset Denoising
AI Lingmei,LIKe,MA Miao
(School of Computing Science,Shaanxi Normal University,Xi'an 710119,China)
The acquisition process of gene expression dataset mixed with noise easily,the noise can interfere with data expression correctly which w ill affect their further analysis and research.The Empirical Mode Decomposition(EMD)denoising of using median-calculation to estimate noise standard deviations that exists some drawbacks and affects the denoising effectiveness.Under the EMD,the fractional Gaussian noise(fGn)model can provide more accurate estimation way of noise standard deviations,denoising on this model can reduce white and colored noise,which w ill enhance the denoising effectiveness.So a denoising scheme based on fGn is proposed on the basis of median-calculation EMD denoising and done the denoising analysis on colon cancer gene expression dataset.Experimental results show that,the values of signal-to-noise,noise rejection ratio,t-test,etc.in advanced method have a certain superiority compared with median-calculation EMD denoising,which can be used as an reference means of denoising to the gene expression dataset.
gene expression dataset;Empirical M ode Decomposition(EMD)denoising;noise standard deviations;fractional Gaussian noise(fGn);colon cancer
艾玲梅,李 科,马 苗.fGn模型在结肠癌基因表达数据集去噪中的应用[J].计算机工程,2015,41(11):303-307.
英文引用格式:Ai Lingmei,Li Ke,M a Miao.Application of fGn Model in Colon Cancer Gene Expression Dataset Denoising[J].Computer Engineering,2015,41(11):303-307.
1000-3428(2015)11-0303-05
A
TP391
10.3969/j.issn.1000-3428.2015.11.052
陕西省重点实验室开放共享基金资助项目(SA IIP201202);陕西师范大学学习科学交叉学科培育计划基金资助项目。
艾玲梅(1965-),女,通讯作者,副教授、博士,主研方向:生物医学信号处理;李 科,硕士研究生;马 苗,教授、博士。
2014-10-15
2014-12-14 E-m ail:1427147182@qq.com

