基于灰度空间相关性最大类间方差的图像分割
贺建峰,符 增,相 艳,易三莉,崔 锐
(昆明理工大学信息工程与自动化学院,昆明650500)
基于灰度空间相关性最大类间方差的图像分割
贺建峰,符 增,相 艳,易三莉,崔 锐
(昆明理工大学信息工程与自动化学院,昆明650500)
一维最大类间方差1D-Otsu和二维最大类间方差2D-Otsu在目标和背景比较模糊时,图像分割效果较差。针对该问题,提出一种基于灰度空间相关性(GLSC)最大类间方差的图像分割算法。该算法使用各像素的灰度值与其邻域内相似像素的数目构建直方图,通过计算GLSC直方图的最大类间方差得到分割阈值,应用积分图的思想将运算复杂度由O((N2×L)2)降到O(N2×L),节省了运算时间。针对5幅大小不同和直方图类型不同的真实图像,与1DOtsu、2D-Otsu和灰度空间相关性熵算法进行分割实验比较,结果表明该算法具有较好的鲁棒性。
最大类间方差;灰度空间相关性;直方图;积分图;图像分割;熵算法
1 概述
一般来说,图像分割方法可以分成4类,即阈值分割、基于边界的分割、基于区域的分割和混合的分割技术[1]。在以上的分割技术中,阈值分割是最简单和有效的一种分割方法。它是在待处理图像中选择一个能够辨别图像背景和目标的阈值进行判别,若低于该阈值就作为图像的背景,高于该阈值则作为图像的目标。
在过去的几十年中,国内外学者提出了大量的阈值选取方法,如基于最大类间方差(Otsu)[2-4]、各种熵[5-7]和模糊集[8-10]等多种类型的阈值选取方法。Otsu方法是一种全局的自动非参数无监督的阈值选取算法,它是基于类间方差为最大的测度准则[11]。熵方法是运用信息论原理解决图像分割问题的一种方法。模糊集理论运用描述图像信息中的模糊性来分割图像。以上面3种原理为基础的阈值分割算法,其共同点是先构建图像直方图,然后选用适当的方法寻找最佳阈值[2,5,8]。
在构建图像直方图过程中,现有的一维阈值方法共同缺点是忽略了图像不同灰度层次的空间相关性。只有包含更多图像信息才能更好地分割图像。为此,在熵阈值方法中,以文献[5]为基础,文献[6,12-13]利用像素灰度和邻域平均灰度构建了二维直方图,然后再利用有关熵的阈值方法确定最佳阈值。在模糊集方法中,以文献[8]为基础,文献[9]将二维直方图方法运用于模糊集理论中。在Otsu阈值方法中,以Otsu[2]理论为基础,提出2D-Otsu算法[3]。在2DOtsu算法的基础上,在构建二维直方图的过程中,又加入了邻域灰度的中值作为特征,形成了三维直方图[4,14],并运用Otsu阈值方法来寻找最佳阈值。然而高维直方图理论存在算法复杂度高和可能丢失有用信息的缺点[15]。
近年来,许多学者提出了一些新的构建直方图的思想。文献[16-17]于2010年提出了灰度空间相关性(Gray-level Spatial Correlation,GLSC)直方图,即使用各像素的灰度值与其邻域内相似像素的数目所创建而成,并将该思想与熵阈值方法相结合来分割图像,得到了不错的分割效果。文献[10]于2011年在GLSC直方图中嵌入了人类视觉非线性特征(Human V isual Nonlinearity Characteristics,HVNC),并利用类型2模糊集的阈值方法来选择最佳阈值,也得到了很好的分割效果。2013年Yim it[18]引进了灰度和方向梯度来辨别像素的空间信息,提出了灰度-方向梯度熵算法,但是仅运用梯度方向很难描述图像的边缘属性。2014年Xiao[19]提出了灰度-梯度幅度直方图,并运用熵的阈值方法寻找图像的最佳阈值,该方法更依赖于图像轮廓的提取。当轮廓模糊时,其区分边缘的能力较差。
针对目标和背景比较模糊的图像,边缘被认为是比目标和背景更为重要的信息,GLSC直方图在突出边缘信息方面有其独特的优势[17]。X iao于2014年验证了Otsu的阈值方法比大多数熵的阈值方法对阈值分割有更好的效果[19]。为此,本文将GLSC直方图与Otsu算法相结合。提出一种新的基于灰度空间相关性最大类间方差的图像分割算法(GLSC-Otsu)。构建邻域为N×N的GLSC直方图,计算GLSC直方图的最大类间方差,将得到的类间方法值乘以关于m(在相同像素值中,其邻域的相似像素个数的总数)和N的加权非线性函数。最佳阈值为当GLSC直方图的类间方差与加权非线性函数乘积取最大值时所得到的解,同时还引进了V iola[20]提出的积分图思想对GLSC-Otsu进行快速阈值选择,降低算法运算复杂度。
2 灰度空间相关性直方图的创建
令f(x,y)为图像大小为Q×R即F={f(x,y)|x∈{1,2,…,Q},y∈{1,2,…,R}}位于(x,y)处的灰度值。构建GLSC直方图如下:对于位于(x,y)处的像素点而言,设g(x,y)表示像素相邻取N×N时,相似像素的个数,其中,N通常取奇数。g(x,y)的计算方法为:
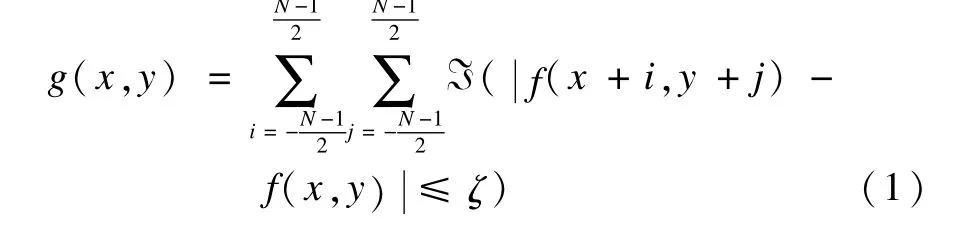
其中:
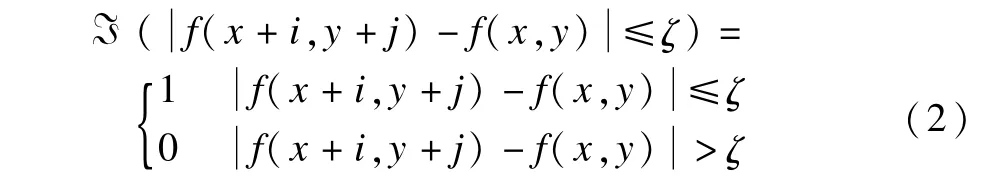
ζ表示归类为相似像素的幅度值(如:若ζ=3,表示在a±3的范围内的像素值都与像素a相似)。
本文运用图像灰度值f(x,y)和邻域像素相似个数g(x,y)来创建GLSC直方图,计算公式为:
p(k,m)=Prob(f(x,y)=k and g(x,y)=m)(3)其中,k为图像灰度值,k∈{0,1,…,255};m为邻域像素相似个数,m∈{1,2,…,N×N};p(k,m)为统计整幅图像中,以像素灰度值k为中心的N×N邻域内,及其像素值相似数目为m的像素个数与整幅图像的像素总数的比值,其具体的计算公式为:

其中,f(k,m)表示统计整幅图像中,以像素灰度值k为中心的N×N邻域内,与其像素值相似数目为m的像素个数;S×R表示整幅图像的像素总数。取ζ=3和N=17,所建的GLSC直方图如图1所示。
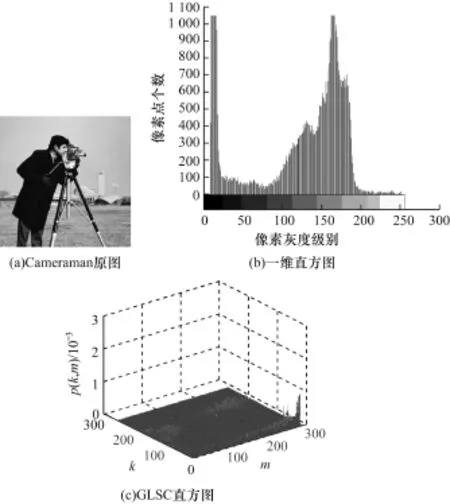
图1 Cam eram an原图、一维直方图和GLSC直方图
3 GLSC最大类间方差分割法
由图1(c)可得,将图像直方图划分成了256× 289的二维直方图,其平面简图如图2所示。
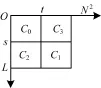
图2 GLSC直方图平面简图
假设图像的分割阈值为(s,t),可以将直方图划分成C0,C1,C2,和C34类,它们分别代表边缘、物体、噪声和背景,具有4个不同的概率密度函数分布。那么它们出现的概率分别为:
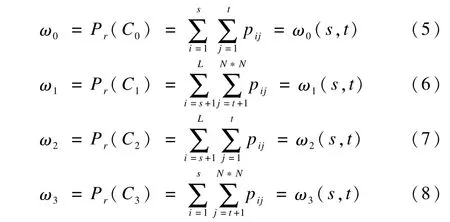
4类对应的均值矢量μ0,μ1,μ2和μ3分别为:

定义一个类间的离散矩阵如式(14)所示,矩阵SB的迹作为类间的离散度测量,且由式(9)~式(12)可得μ0i=μi0/ω0;μ1i=μi1/ω1;μ2i=μi2/ω2;μ3i=μi3/ω3;μ0j=μj0/ω0;μ1j=μj1/ω1;μ2j=μj2/ω2和μ3j=μj3/ω3。
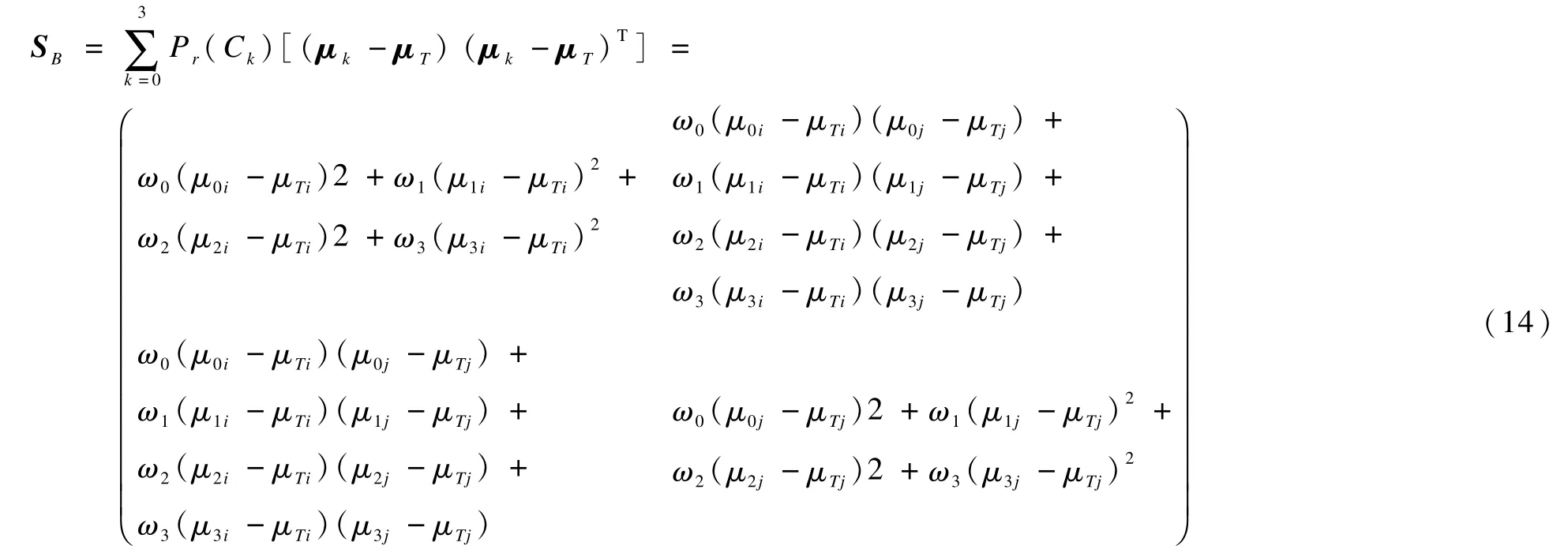
即trSB可得如式(15)所示:

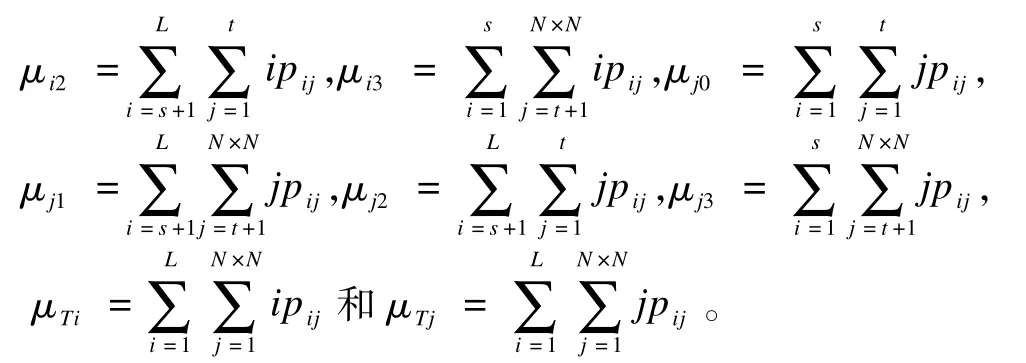
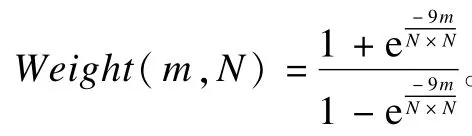
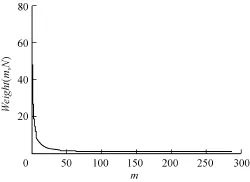
图3 N=17时的函数曲线
最佳阈值(s*,t*)满足下式:
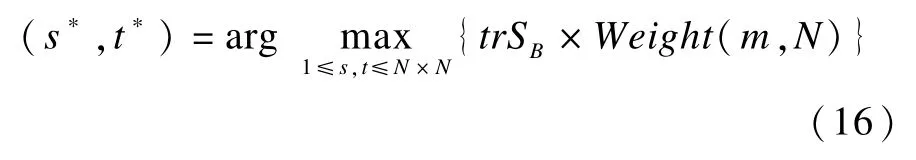
为了求得最佳阈值,需要在N2×L的投影平面内搜索。每一个阈值都会把投影平面划分成4个区域。因此,若忽略直方图的提取时间,灰度空间相关性最大类间方差法的计算复杂度性为:
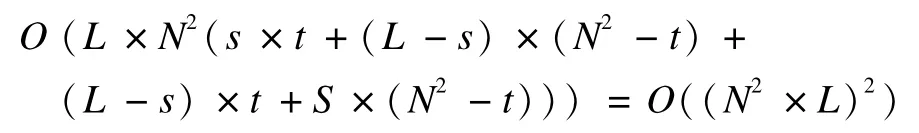
随着N值得增大计算复杂度呈指数增长,无疑限制了本文方法的运用。为此,本文提出了采用积分图快速选取阈值的方法。
4 积分图快速选取阈值方法
积分图是用来求图像特征值时提出的概念[20-21]。在积分图(x,y)的位置是在原图(x′,y′)位置左上角所有的像素之和。其示意图如图4所示,ii(x,y)为左上角阴影部分的像素之和。具体的定义为:

其中,ii(x,y)表示积分图;i(x′,y′)表示原图。
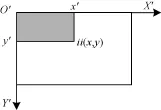
图4 积分图原理
从上一节算法公式可以看出,计算trSB需要计算ω0,ω1,ω2,ω3,μi0,μi1,μi2,μi3,μj0,μj1,μj2,μj3,μTi和μTj。对于同一副图像,μTi和μTj是固定的。对于每一个阈值(s*,t*),如果每次计算类间离散度测量trSB都必须重新从i=0,j=0开始计算。由上一节分析得计算复杂度为O((N2×L)2)。本文运用积分图的思想快速选择阈值。
设生成的GLSC直方图为ω对应的积分图为ω-ii,即ω0,ω1,ω2和ω3计算公式如下:
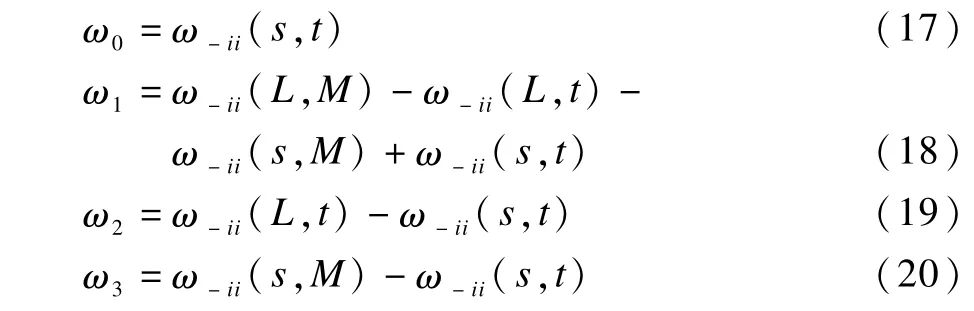
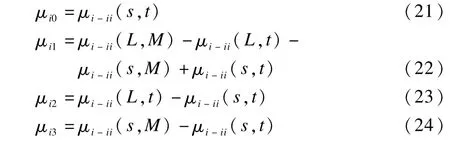
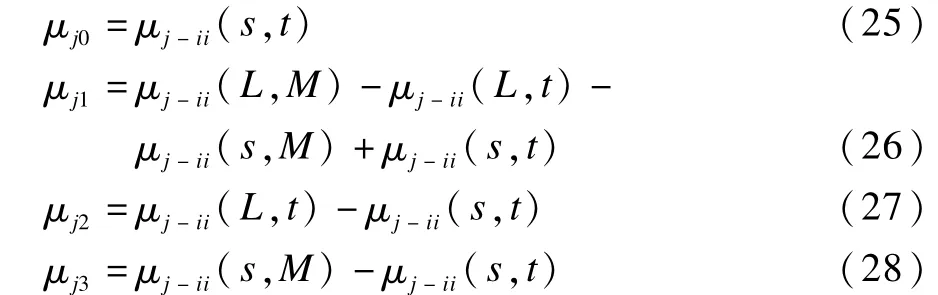
上述方法将求不同区域的概率,最多只要经过几步加减算法即可得到。计算μi0,μi1,μi2,μi3和μj0,μj1,μj2,μj3时,只需先进行一维的计算,然后经过加减法运算即可得到。这样就将时间复杂度L((N2×L)2)降到了L(N2×L)。大大的节省了运行时间和存储空间。
5 仿真结果与分析
在本文实验中,选取5幅不同大小和不同直方图分布类型的真实图像,来测试本文算法的有效性和鲁棒性。它们分别是Ant(357×370像素)、Bacteria(364×364像素)、Block(244×244像素)、Cameraman(256×256像素)和Laser(304×233像素)。
表1列出了当取N=17,而ζ=1,2,…,9时分割该5幅图像的最佳阈值。以分类错误率[10,19]为标准,当取ζ=3时,整体能产生最好的分割效果。本文针对邻域大小为3×3,5×5,7×7,9×9,11×11,13×13,15×15和19×19用相同的方法进行实验,实验表明当N=17,ζ=3时分割效果最佳。下面的实验本文方法的参数取N=17和ζ=3。实验是在3.20 GHz CPU和4 GB内存的PC机,M atlab7.1环境中进行的。

表1 不同ζ所得的最佳阈值
如图5~图14所示,本文算法与1D-Otsu理论[2]、2D-Otsu理论[3]和GLSC KSW熵理论[16-17]进行比较。

图5 Ant的分割结果

图6 Ant的直方图

图7 Bacteria的分割结果
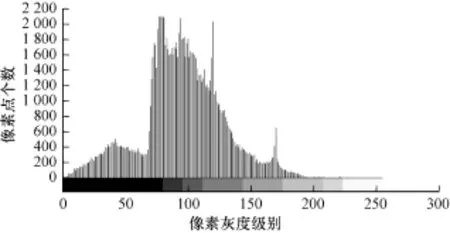
图8 Bacteria的直方图

图9 Block的分割结果
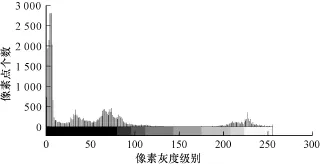
图10 Block的直方图

图11 Cam eram an的分割结果
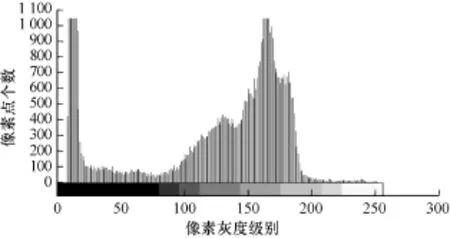
图12 Cam eram an的直方图

图13 Laser的分割结果
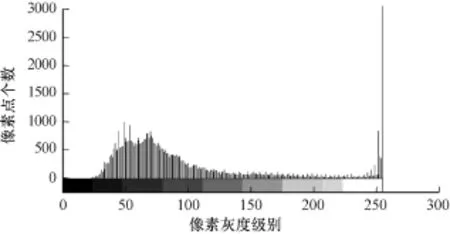
图14 Laser的直方图
本文运用分类错误率来判断分割的性能[10,19]。给出如下公式:
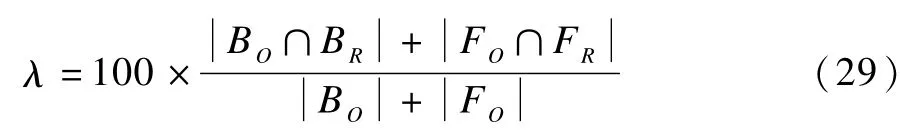
其中,λ∈[0,1],其值越接近1,表明分割效果越好;BO和FO分别代表分割后标准图像的前景和背景;BR和FR分别代表分割后图像的前景和背景;表示一组基数。
不同算法依据上述评价所得的分割精度如表2所示,其中,加粗的数据表示最优数据。表2中的平均分割精度()和标准差(σ)用于评估不同算法整体的有效性和鲁棒性。
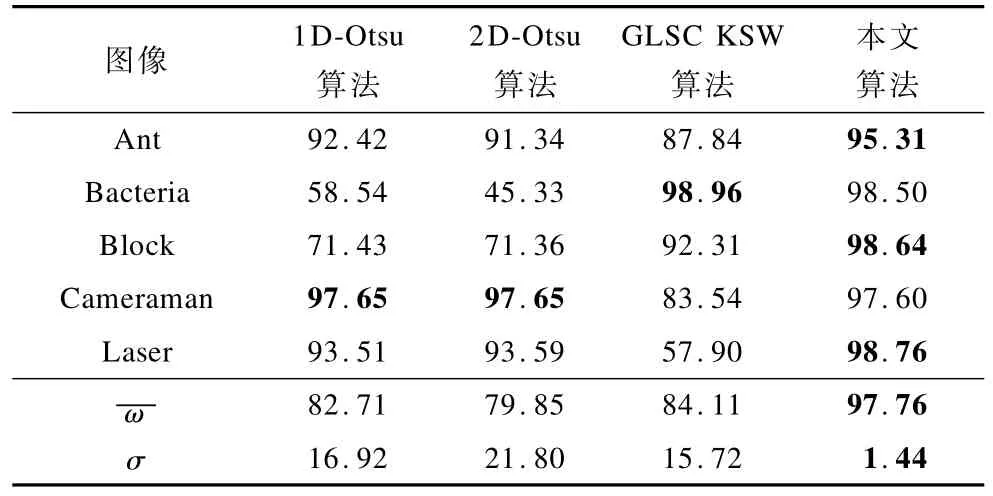
表2 不同算法所得分割精度%
表3和表4分别显示了不同算法的阈值和不同算法所消耗的时间。
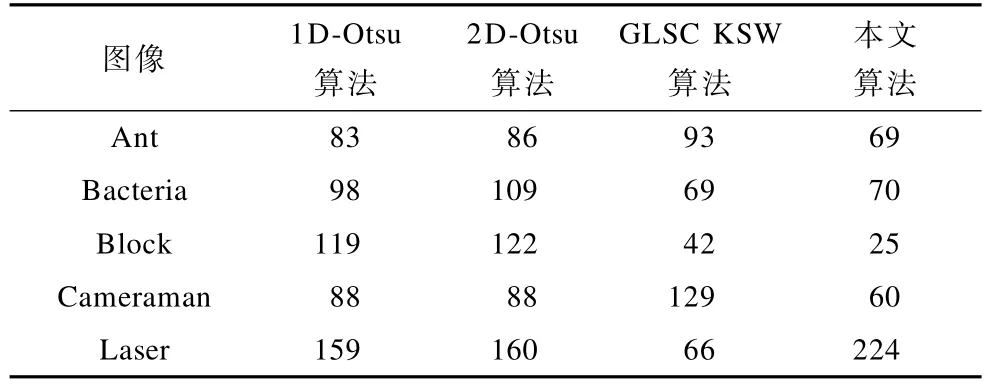
表3 不同算法所得的分割阈值
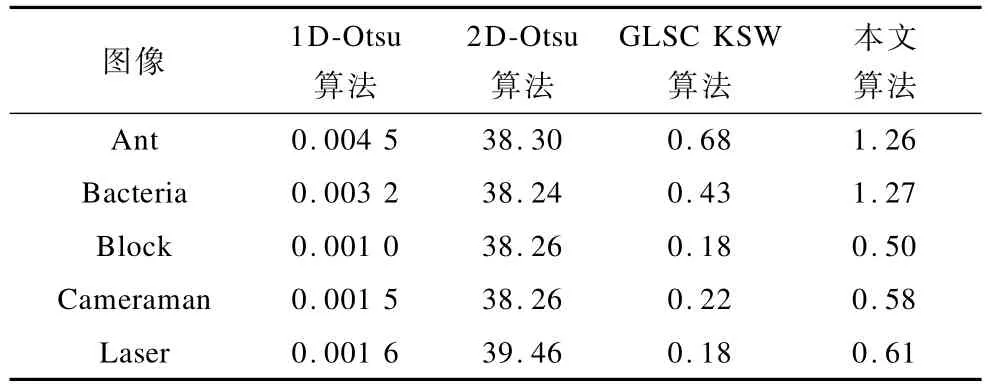
表4 不同算法所消耗的时间s
可以看出:
(1)1D-Otsu和2D-Otsu对图Bacteria和Block的分割效果都比较差,因为这3幅图的目标和背景界限模糊,这2种算法很难区分背景和目标的边缘,导致了分割效果不佳。
(2)GLSC KSW熵算法虽然针对Bacteria最好的分割效果,但是其他图像都不如本文算法的效果。因为关于熵的阈值方法原理不同于Otsu的阈值方法,该方法在大多数情况下分割图像比Otsu的阈值方法要差[19]。
(3)基于灰度空间相关性最大类间方差的图像分割算法在绝大多数情况下都能得到最佳的分割效果。该算法与其他3种算法比较,它具有最高平均分割精度(97.76%)和最低的标准差(1.44%)。
(4)表4对比了不同方法分割图像所消耗的时间,本文算法较1D-Otsu慢,但是比2D-Otsu快了很多。与GLSC KSW算法速度相差不大,因为算法复杂度都是O(N2×L),但是由于本文算法的N值为17,而GLSC KSW熵算法的N取3,这样导致了本文算法慢于GLSC KSW熵算法。因此,以上实验数据都证明了本文算法对分割自然图像具有较好的有效性和鲁棒性。
6 结束语
本文提出一种基于灰度空间相关性最大类间方差的图像分割方法。该算法比1D-Otsu和2D-Otsu算法在构建直方图方法上具有更强的分辨边缘的能力,比GLSC KSW熵算法具有更好的寻找阈值的能力。本文通过使用5幅大小不同和具有不同直方图类型的自然图像进行分割实验比较,结果表明,该算法较其他算法具有更好的有效性和鲁棒性,时间消耗介于2D-Otsu算法与1D-Otsu算法之间,且与GLSC KSW熵算法的计算复杂度相当。另外,本文在寻找参数时做了大量实验,针对不同类型图像,其最佳参数的取值可能会不同。因此,下一步的工作内容是在构建灰度相关信息直方图前,分析待分割图像的先验信息,并将其嵌入到直方图中寻找最佳参数。
[1] Shih F Y.Image Processing and Pattern Recognition:Fundamentals and Techniques[M].Hoboken,USA:John Wiley&Sons,2010.
[2] Nobuyuki O.A Threshold Selection Method from Graylevel Histogram[J].IEEE Transactions on System M an and Cybernetics,1979,9(1):62-66.
[3] 刘建庄,栗文青.灰度图像的二维Otsu自动阈值分割法[J].自动化学报,1993,19(1):101-105.
[4] 景晓军,李剑锋,刘郁林.一种基于三维最大类间方差的图像分割算法[J].电子学报,2003,31(9):1281-1285.
[5] Kapur JN,Sahoo P K,W ong A K C A.New Method for Gray-level Picture Thresholding Using the Entropy of the Histogram[J].Computing Vision,Graphics,and Image Processing,1985,29(3):273-285.
[6] Ahmed A S.Automatic Thresholding of Gray-level Pictures Using Two-dimensional Entropy[J].Computer Vision,Graphics,and Image Processing,1989,47(1):22-32.
[7] 张书真.基于三维直方图修正和灰度熵分解的图像分割[J].计算机工程,2014,40(5):234-237,242.
[8] Huang Liangkai,Wang Maoyun.Image Thresholding by Minimizing the Measure of Fuzziness[J].Pattern Recognition,1995,28(1):41-51.
[9] W ang Qing,Chi Zheru,Zhao Rongchun.Image Thresholding by Maximizing the Index of Nonfuzziness of the 2-D Grayscale Histogram[J].Computer Vision and Image Understanding,2002,85(1):100-116.
[10] X iao Yang,Cao Zhiguo,Zhuo W en.Type-2 Fuzzy Thresholding Using GLSC Histogram of Hum an Visual Nonlinearity Characteristics[J].Optics Express,2011,19(11):10656-10672.
[11] 王海洋,潘德炉,夏德深.二维Otsu自适应阈值选取算法的快速实现[J].自动化学报,2007,33(9):968-971.
[12] Sahoo P K,Arora G A.Thresholding Method Based on Two-dimensional Renyi's Entropy[J].Pattern Recognition,2004,37(6):1149-1161.
[13] Sahoo P K,Arora G.Im age Thresholding Using Twodimensional Tsallis-Havrda-Charvát Entropy[J].Pattern Recognition Letters,2006,27(6):520-528.
[14] 张 健,沈春裕,卢 瑾.基于分解的三维Otsu运动车辆检测方法[J].计算机工程,2013,39(2):172-177.
[15] 陈 琪,熊博莅,陆 军,等.改进的二维Otsu图像分割方法及其快速实现[J].电子与信息学报,2010,32(5):1100-1104.
[16] Xiao Yang,Cao Zhiguo,Zhang Tianxu.Entropic Thresholding Based on Gray-level Spatial Correlation Histogram[C]// Proceedings of IEEE Conference on Pattern Recognition. Washington D.C.,USA:IEEE Press,2008:1-4.
[17] Xiao Yang,Cao Zhiguo,Zhong Sheng.New Entropic Thresholding Approach Using Gray-level Spatial Correlation Histogram[J].Optical Engineering,2010,49(12).
[18] Yim it A,Hagihara Y,Miyoshi T,et al.2-D Direction Histogram Based Entropic Thresholding[J].Neuro Computing,2013,120(23):287-297.
[19] Xiao Yang,Cao Zhiguo,Yuan Junsong.Entropic Image Thresholding Based on GLGM Histogram[J].Pattern Recognition Letters,2014,40(1):47-55.
[20] Viola P,Jones M.Rapid Object Detection Using a Boosted Cascade of Simple Features[J].Computing Vision and Pattern Recognition,2001,14(1):8-14.
[21] 傅红普,邹北骥.方向梯度直方图及其扩展[J].计算机工程,2013,39(5):212-217.
编辑 刘冰
Image Segmentation Based on G ray-level Spatial Correlation Maxim um Between-cluster Variance
HE Jianfeng,FU Zeng,XIANG Yan,YI Sanli,CUI Rui
(School of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China)
W hen processing an image with the blurred background and target,image segmenting effect by maximum between cluster variance 1D-Otsu and 2D-Otsu is not good.A method for image segmentation based on Gray-level Spatial Correlation(GLSC)maximum between-cluster variance is proposed.The proposed algorithm uses the gray value of the pixels and their similarity with neighboring pixels in gray value to build a histogram which is called GLSC histogram. Then threshold value is obtained by calculating GLSC histogram maximum between-class variance.Integrogram is introduced in order to make the time complexity reduced from original O((N2×L)2)to O(N2×L).Comparing the proposed algorithm wth 1D-Otsu,2D-Otsu and GLSC entropy algorithm for segmenting 5 different real images,the proposed algorithm show s better robustness.
maximum between-cluster variance;Gray-level Spatial Correlation(GLSC);histogram;integrogram;image segmentation;entropy algorithm
贺建峰,符 增,相 艳,等.基于灰度空间相关性最大类间方差的图像分割[J].计算机工程,2015,41(11):280-286.
英文引用格式:He Jianfeng,Fu Zeng,Xiang Yan,et al.Image Segmentation Based on Gray-level Spatial Correlation Maximum Between-cluster Variance[J].Computer Engineering,2015,41(11):280-286.
1000-3428(2015)11-0280-07
A
TP391.4
10.3969/j.issn.1000-3428.2015.11.048
国家自然科学基金资助项目(11265007);教育部留学回国人员科研启动基金资助项目(2010-1561)。
贺建峰(1965-),男,教授、博士,主研方向:图形图像处理,模式识别;符 增,硕士研究生;相 艳,讲师、硕士;易三莉,讲师、博士;崔 锐,硕士研究生。
2014-11-18
2014-12-18 E-m ail:jfenghe@qq.com

