基于集对势优势关系的变精度粗糙集模型

曹炳汝，刘 勇

（江南大学商学院，江苏无锡214122）

·先进计算与数据处理·

基于集对势优势关系的变精度粗糙集模型

曹炳汝，刘 勇

（江南大学商学院，江苏无锡214122）

针对不完备信息系统含有偏好信息、噪音数据、模糊性等属性的特点，利用集对分析、优势关系和变精度粗糙集，构建一种在集对势优势关系基础上的变精度粗糙集模型。对存在属性值缺失的序值信息系统，利用集对分析方法，定义基于α联系度系数的集对势优势关系，代替变精度粗糙集模型的等价关系，并给出一种新的变精度粗糙集模型。实例分析结果验证了该模型的有效性与合理性。

不完备信息系统；优势关系；集对势；粗糙集；属性集

1 概述

作为一种处理具有不精确性、不确定性和模糊性的方法［1］，粗糙集基于等价关系（即满足自反性、对称性和传递性的关系），定义对象集的下、上近似，由于其具有强大的并行计算和数据处理能力，被广泛地运用在知识发现、数据挖掘、决策分析和模式识别等领域［2-4］。粗糙集的研究对象是属性值已知且离散的完备信息系统，然而由于现实世界的复杂性、不确定性以及人类认知的有限性，信息系统属性值并不是都是已知的，一些属性值存在缺失等问题，这样一些信息系统往往是不完备序值信息系统。

为了处理不完备序值信息系统，一些专家、学者尝试利用不同的方式、方法从填补构造完备信息系统和直接处理不完备信息系统2个方面着手展开研究。在填补和构造完备信息系统方面，目前的研究主要是对不完备信息系统进行预处理，即根据不同的规则和属性值特性，补全属性值，使不完备序值信息系统变成完备信息系统，而后再利用粗糙集方法进行决策分析、模式识别等［5］。此类处理不完备序值信息系统的方法容易造成不完备信息系统信息丢失。在直接处理不完备信息系统方面，主要是基于模糊集、灰色系统、集对分析等方法构建模糊关系［6-7］、容差关系［8-10］、相似关系［11-12］、优势关系［13-16］的粗糙集模型，并利用其识别不完备信息系统中影响粗糙集分类的因素，获取决策规则，而单单基于容错关系、相似关系、优势关系的粗糙集在处理不完备信息系统进行分类时，当条件属性较多时，粗糙集集合的定义便会过于宽松，以致于难以满足实际需要，鉴于此，一些专家、学者尝试利用集对分析方法对不完备信息系统进行处理［17］，构建基于分析的粗糙集模型［18-20］。通过比较基于集对分析的粗糙集模型［21-23］，可以发现，其大多是从同一度、不确定性、对立度某一方面考虑对象的分类效果［24-25］，而缺乏从整体考虑所有对象整体分类性能，使得分类结果与实际存在着偏差［26-27］。鉴于此，在借鉴和比较文献［19，22，26-27］的集对势相关研究成果的基础上，本文针对不完备信息系统中含有偏好信息、噪音数据、模糊性等属性的信息，构建一种新的优势变精度粗糙集模型。

2 集对势优势关系

为了处理不完备序值信息系统的偏好属性，Greco等学者提出了优势粗糙集理论，该理论能够处理多标准决策分析中典型事例决策的不一致性问题，其利用优势关系代替粗糙集的不可分辨关系，并根据逻辑语句“if，…，then”表示的决策规则，由事例决策导出偏好模型［28-29］。借鉴优势粗糙集信息系统，下面定义不完备序值信息系统下的优势关系。

2.1 不完备序值信息系统

定义1 设序值信息系统为S=（U，A，V，f），其中，U=｛x1，x2，…，xn｝为有限非空集合，亦称论域；A=｛AT∪D｝为有限非空属性集合，AT=｛a1，a2，…，am｝为条件属性集合；D=｛d1，d2，…，dp｝为决策属性集合；V=∪Va，对于a∈A，Va为属性a的值域；f：U×A→V为信息函数，对于∀a∈A、∀x∈U，f（x，a）∈Va，它指定了U中每一个对象的属性值。对于序值信息系统S=（U，A，V，f），若至少一个对象x关于属性a，使得f（x，a）∈Va为空值（用*表示），则称序值信息系统S为不完备序值信息系统，记作S*=（U，A，V，f），否则称完备序值信息系统［18］。

定义2 在不完备序值信息系统S*=（U，A，V，f）中，令x，y∈U，B⊆AT，对于∀a∈B，一般意义下的优势关系为：

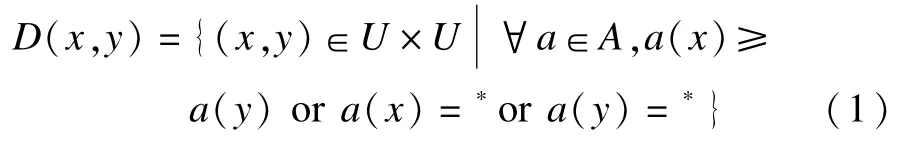
定义3 在不完备序值信息系统为S*=（U，A，V，f）中，给定B⊆AT且x∈U，y∈U，关于x的B-优势集和B-劣势集分别定义如下：

假设根据决策者，将对象集U分为有限数量的决策类，令Cl=｛Clt，t∈｛1，2，…，n｝｝，则：Cln≻…≻Clt≻…≻Cl1，将这些类别向上合并及向下合并可以得出：

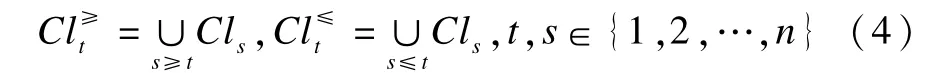
2.2 基于阈值α的集对势优势关系与优势类

作为一种刻画确定性与不确定性及其转化规律的一种系统分析工具，集对分析将被研究的客观事物之确定性联系和不确定性联系作为一个整体来分析和处理。为有效描述和刻画不完备序值信息系统的不确定性，在文献［18-27］研究成果的基础上，重新定义了集对势优势关系及其优势类。

定义4 在不完备信息系统S*=（U，A，V，f）中，对于B⊆A，且，如果X，Y表示任意两对象x，y∈U关于属性集B所构成的集合，H（X，Y）表示在优势关系下集合X，Y所构成的集合对，则称：

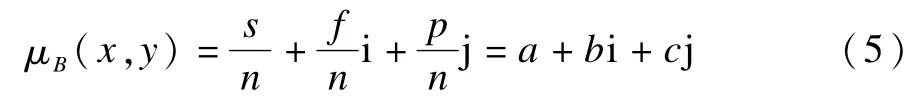
为y在属性集合B上优于x的联系度。

定义5 在不完备信息系统S*=（U，A，V，f）中，对于B⊆A，如果μB（x，y）=a+b i+c j表示x，y关于属性集B的联系度，则称优势度a与对立度c的比值：

为对象x，y关于属性集B在优势关系下的集对势。

若c=0，shi（H）B→∞，则称集对H（X，Y）中对象x，y关于属性集B在优势关系下具有无穷大势，即x关于属性集B远远优于对象y，可简记为shi（H）B→∞。

通过比较文献［18-27］基于集对分析的粗糙集模型，可以发现，其大多是利用集对联系度从同一度、不确定性、对立度某一方面考虑对象的分类效果，而缺乏从整体考虑所有对象整体分类性能。当在处理存在大量空值的不完备序值信息系统时，容易造成分类结果与实际存在偏差。鉴于此，在借鉴文献［19，22，26-27］的集对势相关研究成果的基础上，并针对基于集对粗糙方法上下近似运算性质不完善等问题，利用集对势来定义集对势优势关系。

定义6 在不完备序值信息系统S*=（U，A，V，f）中，对于∀a∈A，∀x，y∈U，B⊆AT，0.5≤α≤1，称：

为对象x，y基于阈值α的集对势优势关系，相应地称D-α（B）对象x，y基于阈值α的集对势劣势关系。

通常同一度阈值0≤α≤1，这里0.5≤α≤1是由同一趋势的无穷大势所满足的条件推出，即a+b+c=1，a＞b，c=0，所以a≥0.5，因为定义a≥α，所以0.5≤α≤1。显然集对势优势关系满足自反性、对称性、传递性。

定义7 在不完备序值信息系统为S*=（U，A，V，f）中，对于∀a∈A，∀x，y∈U，B⊆AT，0.5≤α≤1，称：

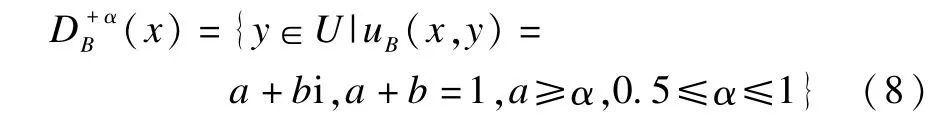
为对象x，y基于阈值α的集对势优势类。

3 变精度粗糙集模型

为有效处理信息系统的噪声数据，Ziarko在粗糙集里通过引入一个阈值β来近似空间，提出了变精度粗糙集模型［30-32］。基于变精度模型，将集对势优势关系替代变精度粗糙集模型的等价关系，构建优势变精度粗糙集。相应地，基于集对势的优势变精度粗糙集的下近似和上近似可以做如下定义。

3.1 模型构建

定义8 在不完备序值信息系统S*=（U，A，V， f）中，给定阈值0.5≤α≤1，0.5＜β≤1，集合D，B⊆AT，则：

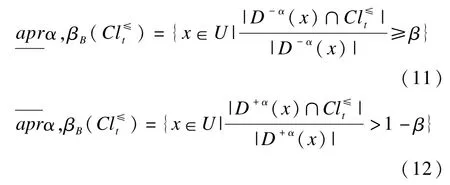
定义9 在不完备序值信息系统S*=（U，AT∪D，V，f）中，基于集对势优势关系的变精度粗糙集的分类质量为：

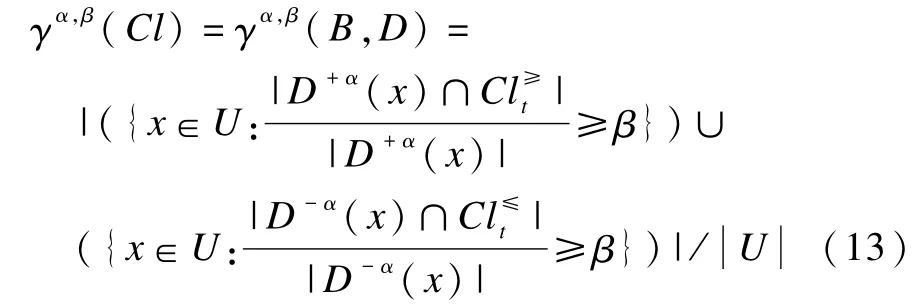
其中，γα，β（B，D）度量了论域中给定阈值α，β可能正确的分类知识在现有知识中的百分比。

3.2 模型性质

定理1 在不完备序值信息系统S*=（U，A，V，f）中，给定任意阈值0.5≤α≤1，0.5＜β≤1，对于集合，∀B⊆AT，则有：

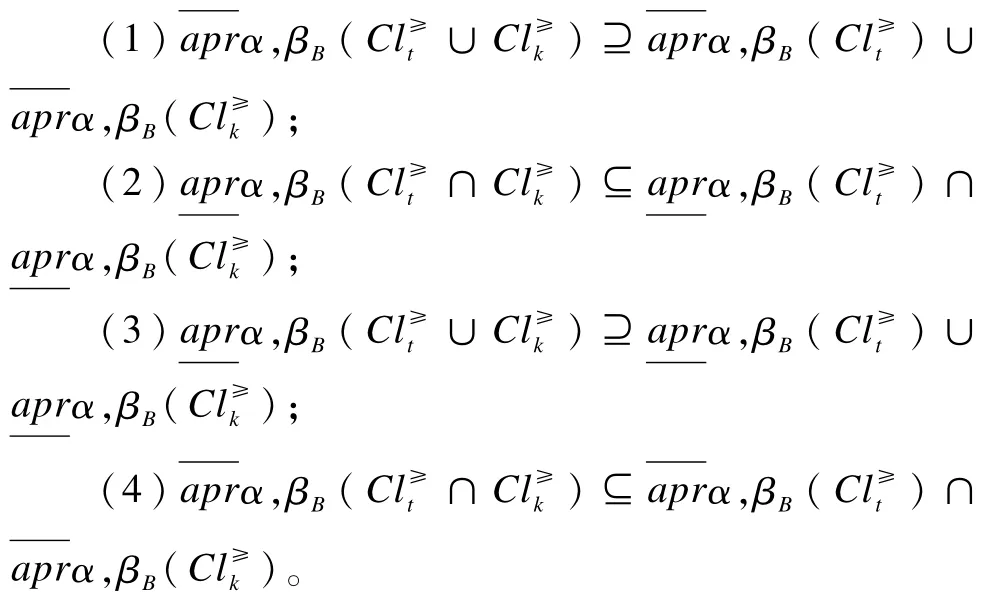
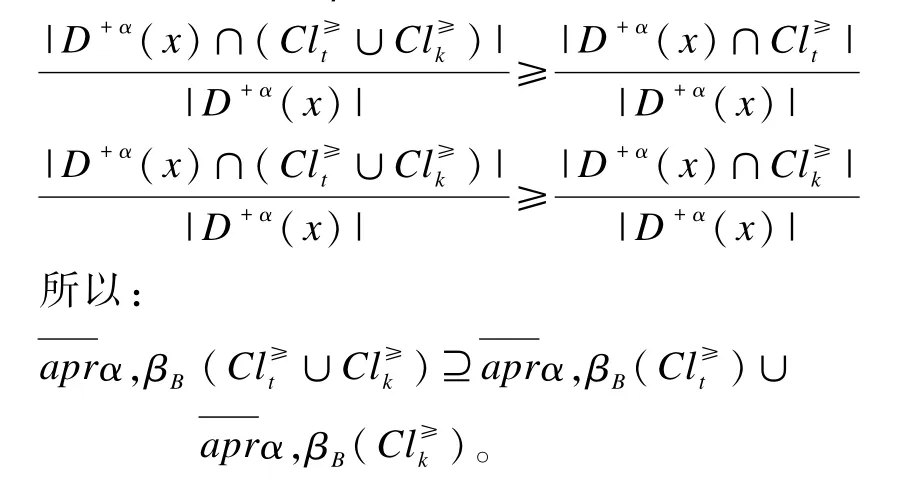
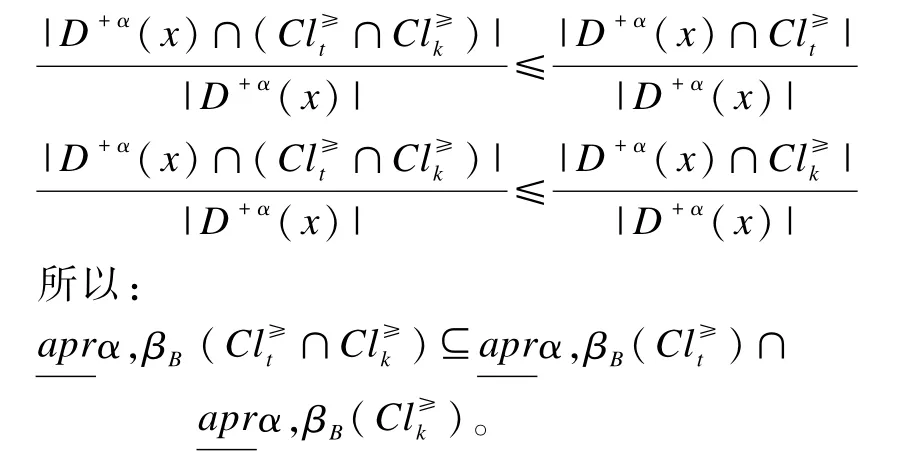
（3）的证明同（1），（4）的证明同（2）。

定理2 在不完备序值信息系统S*=（U，A，V，f）中，给定阈值0.5≤α≤1，0.5＜β≤1，对于集合，则有：

（2）类似（1）证明，略。

定理3 在不完备序值信息系统S*=（U，A，V，f）中，对于∀B⊆C，Clt⊆D，∀t∈｛1，2，…，n｝，及0.5≤α≤1，0.5＜β≤1，则下列关系成立：

定理4 在不完备序值信息系统S*=（U，A，V，f）中，给定任意阈值0.5≤α≤1，0.5＜β≤1，对于集合，则有：

（3）的证明类似于（1），（4）证明类似于（2）。

3.3 属性约简方法

属性约简方法步骤如下：

输入 不完备信息系统S*=（U，A，V，f），集对势阈值α和置信阈值β

输出 不完备信息系统S*=（U，A，V，f）的一个约简B

步骤1 令B=AT；

步骤2 求出系统分类质量γα，β（B，D）；

步骤3 对于每个属性a∈B，计算γα，β（B-a，D）和属性a的重要度Sigα（a）；

步骤4 对于所有满足γα，β（B-a，D）≥γα，β（AT，D）且Sigλ（a）最小，则B=B-｛a｝；若γα，β（B-a，D）＜γα，β（AT，D）且Sigλ（a）都相同，则选择在所有对象取值中空值最多的属性a，B=B-｛a｝；

步骤5 如果对于每个属性a∈B，γα，β（B-a，D）＜γα，β（AT，D），转步骤6，否则转步骤3；

步骤6 输出B，即不完备信息系统S*=（U，A，V，f）的一个约简B。

4 案例分析

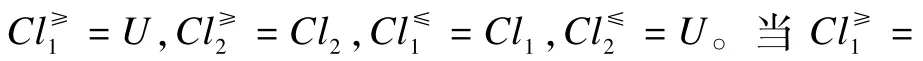
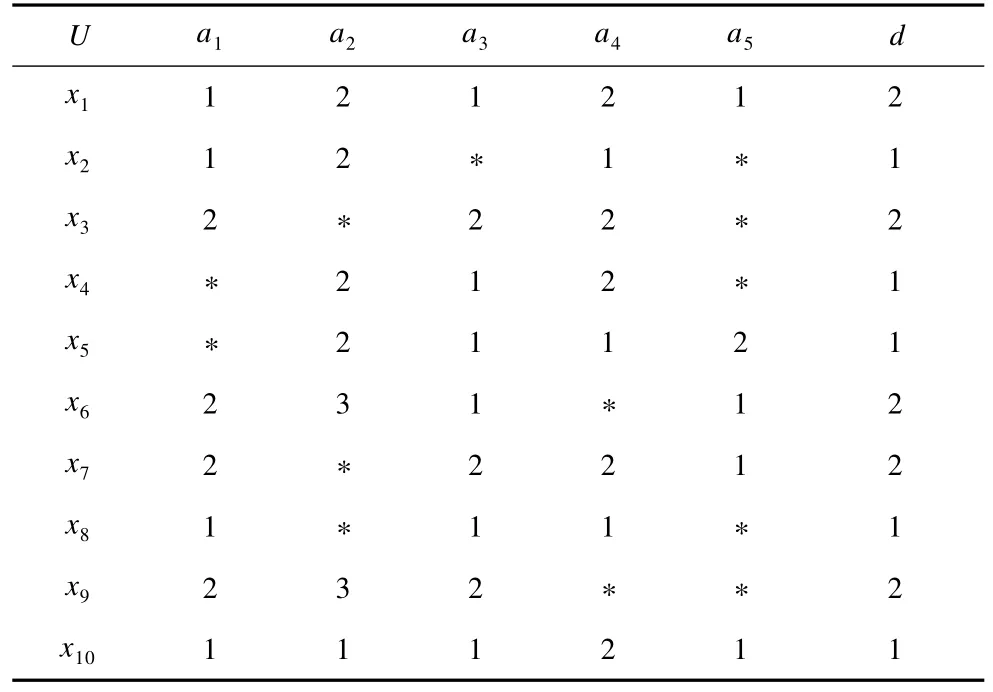
表1 不完备信息系统

当α=0.6时，基于优势关系，根据决策类对论域进行划分，可得如下类别：

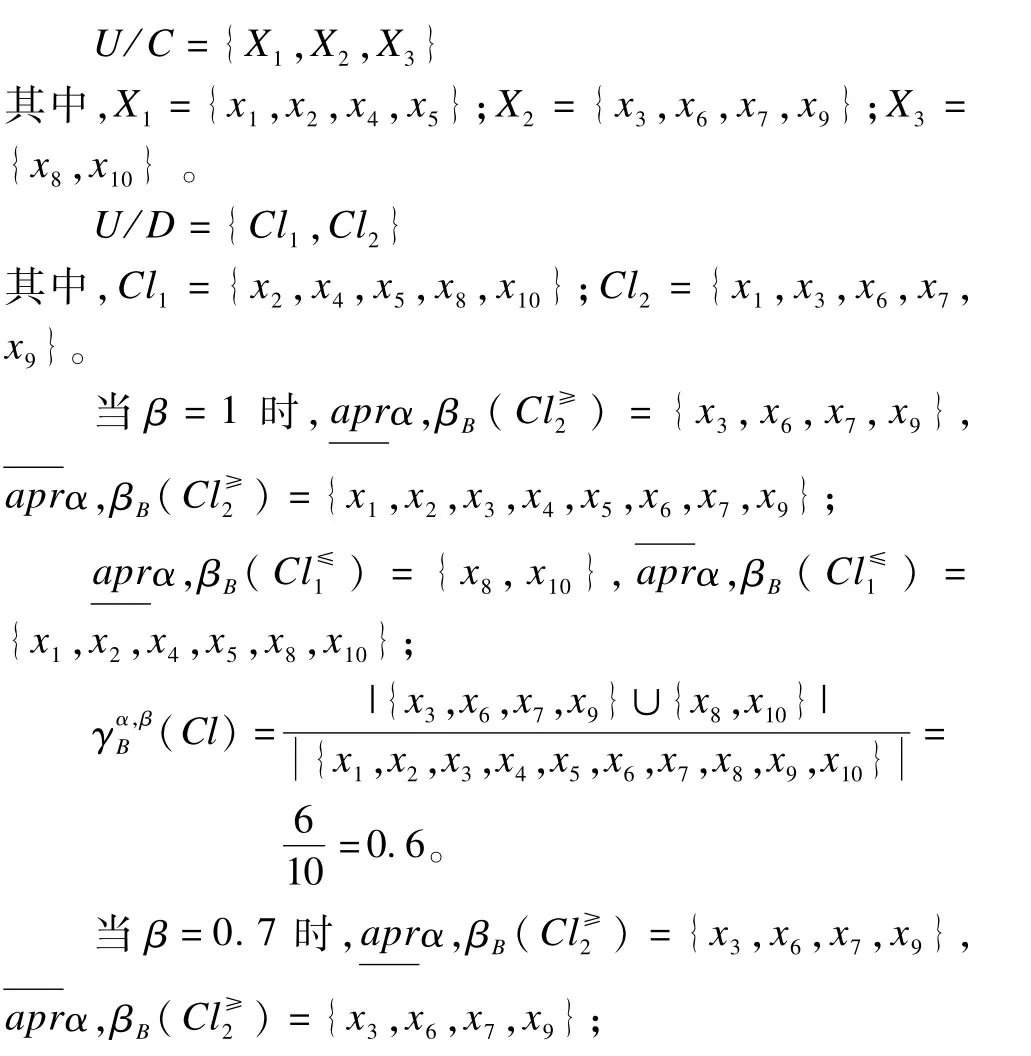
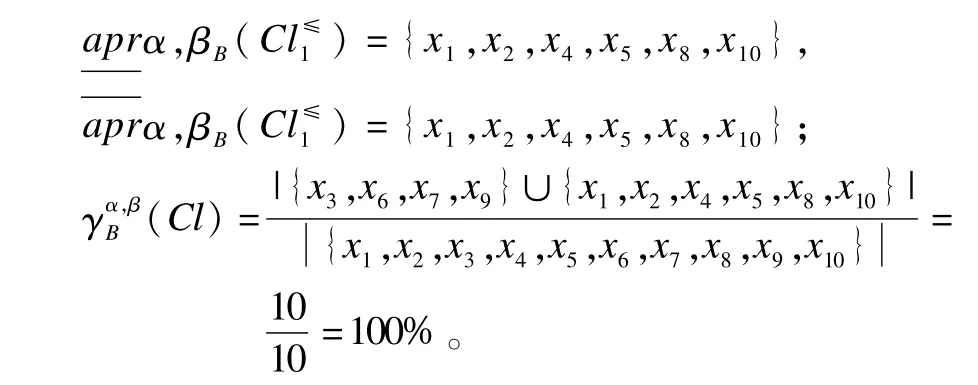
当α=0.6，β=0.7时，根据所设计的属性约简方法，可得其中一个属性约简为｛a1，a2，a3｝，由此约简可得导出的相应的决策规则。由以上计算可知，10对象全部被正确分类，即它们的分类质量为100%。

为进一步说明模型的有效性与合理性，将文献［6，16，19，26-27］所构建的粗糙集模型分别记为模型1～模型5，当α=0.6，β=0.7时，利用这5个模型计算，其计算结果如表2所示。根据表2的计算结果可知，基于这几个模型得到的属性约简一致，而这所构建的模型的分类质量确是最高的。

表2 不同模型计算结果

根据上面的计算和分析可以看出，基于集对势的优势变精度粗糙集模型通过调整参数α和β，具有一定的容错性，并能够实现对对象的正确分类，挖掘决策信息表的知识，提取决策规则。

5 结束语

由于客观世界的复杂性、不确定性以及人类认知的有限性，所获得信息系统往往为不完备信息系统。为此，本文构建了一种基于集对势的优势变精度粗糙集模型。实验结果表明，本文模型能够有效处理含有噪声数据、偏好信息的不完备序值信息，提取决策规则，并且模型通过调整参数α，β具有一定的容错能力。而对于含有灰色信息、模糊信息等不完备信息系统，构建基于集对势的优势灰色变精度粗糙集模型，探讨其适用范围将是下一步研究的内容。

［1］ Pawlak Z.Rough Sets［J］.International Journal of Information and Computing Sciences，1998，49（5）：415-422.

［2］ Pawlak Z，Skowron A.Rudiments of Rough Sets［J］.Information Sciences，2007，177（1）：3-27.

［3］ Pawlak Z，Skowron A.Rough Sets：Some Extensions［J］. Information Sciences，2007，177（1）：28-40.

［4］ Pawlak Z，Skowron A.Rough Sets and Boolean Reasoning［J］.Information Sciences，2007，177（1）：41-73.

［5］ Kryszkiewicz M.Rough Set Approach to Incomplete Information System s［J］.Information Sciences，1998，112（1）：39-49.

［6］ Liu Y，Lin Y，Zhao H H.Variable Precision Intuitionistic Fuzzy Rough Set Model and Application Based on Conflict Distance［J］.Expert System s，2015：32（2）：220-227.

［7］ 刘 勇，菅利荣.杂合灰色聚类与变精度粗糙模糊集的概率决策方法及应用［J］.管理工程学报，2013，27（3）：110-117.

［8］ Kryszkiewicz M.Rough Set Approach to Incomplete Information System s［J］.Information Sciences，1998，112（1）：39-49.

［9］ Stefanow ski J，Tsoukias A.Incomplete Information Tables and Rough Classification［J］.Computational Intelligence，2001，17（1）：545-566.

［10］ 王国胤.Rough集理论在不完备信息系统中的扩充［J］.计算机研究与发展，2002，39（10）：1238-1243.

［11］ 颜锦江，黄 兵.不完备信息系统中基于相似度的变精度粗糙集模型［J］.系统工程理论与实践，2006，（10）：67-72.

［12］ Slowinski R，Vanderpooten D.A Generalized Definition of Rough Approximations Based on Similarity［J］.IEEE Transactions on Know ledge and Data Engineering，2000，12（2）：331-336.

［13］ Greco S，Matarazzo B，Slowiski R.Rough Approximation by Dominance Relations［J］.International Journal of Intelligent Systems，2002，17（1）：153-171.

［14］ Greco S，Matarazzo B，Slowiski R.Rough Sets Theory for Multi-criteria Decision Analysis［J］.European Journal of Operational Research，2002，129（1）：1-47.

［15］ Shao M W，Zhang W X.Dom inance Relation and Rules in an Incomplete Ordered Information System［J］.International Journal of Intelligent Systems，2005，20（2）：13-27.

［16］ Yang X B.Dominance-based Rough Set Approach and Know ledge Reductions in Incomplete Ordered Information System［J］.Information Sciences，2008，178（4）：1219-1234.

［17］ 赵克勤.集对分析及其初步应用［M］.杭州：浙江科学技术出版社，2000.

［18］ 谢 军，宋余庆.不完备序值决策系统中的拓展粗集模型及集对分析［J］.计算机科学，2008，35（12）：154-157.

［19］ 黄 兵，周献中.基于集对分析的不完备信息系统粗糙集模型［J］.计算机科学，2002，29（9）：1-3.

［20］ 黄 兵，周献中.不完备信息系统中基于联系度的粗集模型拓展［J］.系统工程理论与实践，2004，（1）：88-92.

［21］ 刘富春.基于限制容差关系的集对粗糙集模型［J］.计算机科学，2005，32（6）：124-128.

［22］ 刘富春.变集对联系度的扩充粗糙集模型及其属性约简［J］.计算机科学，2006，33（3）：185-187.

［23］ Zhou Lei，Shu Lan.Rough Set Model Based on New set Pair Analysis［J］.Fuzzy System s and Mathematics，2006，20（4）：111-116.

［24］ 徐 怡，李龙澍.基于（α，λ）联系度容差关系的变精度粗糙集模型［J］.自动化学报，2011，37（3）：303-308.

［25］ 陶 志，戴慧君，张 艳.不完备信息系统中集对粗糙集模型［J］.计算机应用，2008，28（7）：1684-1685，1691.

［26］ 徐 怡，李龙澍，李学俊.基于集对势的扩充粗糙集模型［J］.系统仿真学报，2008，20（6）：1515-1518.

［27］ 徐 怡，李龙澍.变精度集对势粗糙集模型［J］.控制与决策，2010，25（11）：1732-1736.

［28］ Greco S，Matarazzo B，Slowiski R.Rough Approximation by Dominance Relations［J］.International Journal of Intelligent Systems，2002，17（2）：153-171.

［29］ Greco S，Matarazzo B，Slowiski R.Rough Sets Theory for Multi-criteria Decision Analysis［J］.European Journal of Operational Research，2001，129（1）：1-47.

［30］ Ziarko W.Variable Precision Rough Set Model［J］. Journal of Computing and System Sciences，1993，46（1）：39-59.

［31］ Ziarko W.Analysis of Uncertain Information in the Framework of Variable Precision Rough Sets［J］. Foundations of Computing and Decision Sciences，1993，18（1）：381-396.

［32］ Ziarko W.Rough Sets，Fuzzy Sets and Know ledge Discovery［M］.Singapore：Springer，1999.

编辑索书志

Variable Precision Rough Set Model Based on Set Pair Situation Dominance Relationship

CAO Bingru，LIU Yong
（School of Business，Jiangnan University，Wuxi214122，China）

In order to deal with the incomplete information system with a variety of noise data，dominance information and other information，and acquire decision rules，the thought and method of the set pair theory，dominance relationship and variable precision rough set are used to construct a novel dominance variable precision rough set model based on set pair situation.With respect to the incomplete information system containing the missing attribute values，by utilizing the set pair analysis method，a set pair situation dominance relationship based on the threshold α connection degree is defined，and it is used to substitute the equivalence relationship of the variable precision rough set model，so that a novel variable precision rough set model based on the set pair situation is established，and its properties are researched.An example show s the feasibility and effectiveness of the proposed model.

incomplete information system；dominance relationship；set pair situation；rough set；attribute set

曹炳汝，刘 勇.基于集对势优势关系的变精度粗糙集模型［J］.计算机工程，2015，41（11）：35-40.

英文引用格式：Cao Bingru，Liu Yong.Variable Precision Rough Set Model Based on Set Pair Situation Dominance Relationship［J］.Computing Engineering，2015，41（11）：35-40.

1000-3428（2015）11-0035-06

A

TP18

10.3969/j.issn.1000-3428.2015.11.007

江苏省社会科学基金资助项目（14GLC008）。

曹炳汝（1960-），男，教授，主研方向：粗糙集，软计算；刘 勇（通讯作者），副教授、博士。

2015-05-05

2015-07-11 E-m ail：clly1985528@163.com