基于改进光滑l0范数的块稀疏信号重构算法

祁 锐，李宏伟，张玉洁

（1.中国地质大学a.地球物理与空间信息学院；b.数学与物理学院，武汉430074；2.海军工程大学理学院，武汉430033）

·开发研究与工程应用·

基于改进光滑l0范数的块稀疏信号重构算法

祁 锐1a，2，李宏伟1b，张玉洁1b

（1.中国地质大学a.地球物理与空间信息学院；b.数学与物理学院，武汉430074；2.海军工程大学理学院，武汉430033）

光滑l0范数算法用带参数的高斯光滑函数序列逼近l0范数，可以用于压缩感知信号重构。块稀疏信号是一种典型的稀疏信号，它的非零元素成块出现。为此，基于改进的光滑l0范数提出一种块稀疏信号重构算法。利用反正切函数取代高斯函数序列，通过对下降因子的优化处理进一步提高收敛效果。仿真实验结果表明，相比块光滑l0范数算法、光滑l0范数算法以及正交匹配追踪算法，该算法具有更好的鲁棒性和更高的信噪比。

压缩感知；块稀疏；光滑l0范数；信号重构

1 概述

文献［1］提出一种新的信号采样理论——压缩感知（Compressed Sensing，CS）。CS在采样的同时完成了信号的压缩，它可以突破Nyquist采样定律的限制对信号进行采样，并完成精确重构。

针对组合优化问题，众多学者已经提出了很多有效的重构算法，包括经典的基追踪（Basis Pursuit，BP）算法［2］和正交贪婪（Orthogonal Greedy A lgorithm，OGA）算法［3-4］，以及光滑l0范数（Smoothed l0Norm，SL0）算法［5］等，但是这些算法是针对传统的稀疏信号，没有考虑到源信号的结构特性。

不同于一般传统信号，有些信号呈现出一种特殊的结构，比如，非零元素成块形式出现，这种信号称为块稀疏信号。针对这种块稀疏信号的特点，学者们进行了深入的研究，提出了许多有效的算法［6-10］。此外，文献［11］将SL0算法推广到块稀疏信号重构问题中，提出了块光滑l0范数（Block Smoothed l0Norm，BSL0）算法.本文结合贪婪算法的快速性和凸优化算法的准确性，研究基于BSL0算法的一种改进算法，用一系列含参数的反正切函数来逼近l0范数，并结合对下降因子σ的处理，使得算法在信噪比和重构时间上取到平衡，称为改进的块光滑l0范数（Improved Block Smoothed l0Norm，IBSL0）。

2 压缩感知与块稀疏信号

2.1 组合优化问题

假定s∈Rm×1是一个未知的源信号，经过测量矩阵A∈Rn×m（n＜m）并满足x=As，得到观测信号x∈Rn×1，由于方程x=As本身是欠定的，因此它存在无穷多个解，于是必须添加一些附加条件以保证解的唯一性。在源信号s稀疏的假设下，恢复源信号s可以通过求解如下的组合优化问题：

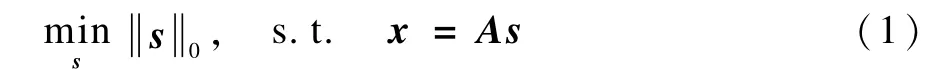
2.2 块稀疏信号压缩感知模型

块稀疏信号压缩感知模型如下：

其中，A∈Rn×m称为测量矩阵，它的元素服从高斯分布或伯努利分布，n＜m；x∈Rn×1是观测信号；s∈Rm×1是块稀疏源信号，具体形式如下：

其中，si（i=1，2，…，N）是源信号s的第i块；d是每块的大小，且满足m=Nd。一个块稀疏信号s称为k-稀疏是指N个块中至多有k个非零块，即有k个不为0，可以看到，如果d=1，这种块稀疏模型退化成传统的稀疏信号模型。

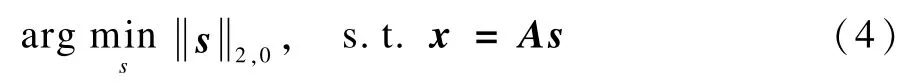
I（x）是示性函数，且满足：

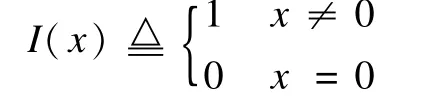
2.3 重构算法

目前块稀疏信号的重构主要基于以下4种算法：

（1）L-OPT算法。由于求解式（4）是一个NP-难问题，因此文献［6］利用信号的块稀疏特性，将l1范数最小化的思想移植到问题式（4），将其转化为如下的混合l2/l1范数凸优化问题来求解：

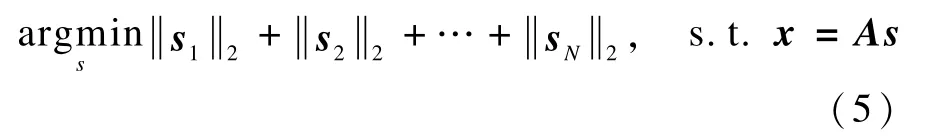
文献［12］进一步证明了在满足一定条件下，可以用式（5）精确地恢复任意的块稀疏源信号。

（2）针对块稀疏信号的贪婪类算法［7］。将经典的贪婪类算法——正交匹配追踪（Orthogonal M atching Pursuit，OMP）算法拓展到块稀疏信号中，得到针对块稀疏信号的块正交匹配追踪（Block OMP，BOMP）算法。以BOMP为例，该算法主要由3个部分构成：相关最大化，更新信号支撑块，更新残差。其中，算法在每次相关最大化操作时只找到一个信号支撑块，对于块稀疏度为k的信号，至少需要k次迭代才能恢复源信号，算法效率偏低。

（3）基于混合l2/lp范数的非凸优化算法［8］。它的主要思想是将块稀疏信号的范数最小化问题转化为如下的非凸优化问题：

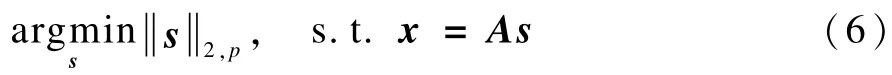
其中：

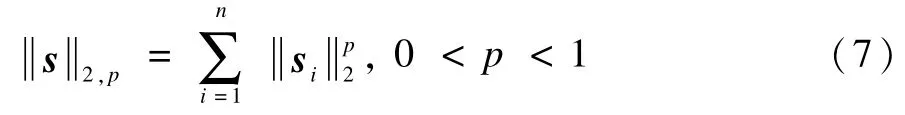
实验结果说明该算法要优于混合l2/l1范数凸优化算法。

（4）将SL0算法推广到块稀疏信号中的BSL0算法［11］。BSL0相当于将SL0算法应用到块稀疏信号中，将块稀疏信号的范数最小化问题用一系列高斯函数序列去逼近。

3 本文算法

假定源信号s是一个k-稀疏信号，求解式（1）的l0范数最小化问题需要穷举所有的Ckm种可能，随着源信号维数m的增大，它将会非常难以实现。文献［5］提出了光滑l0范数（SL0）算法，该算法的主要思想是用连续的高斯函数序列去逼近不连续的l0范数，考虑高斯函数，很明显有：

因此，定义：

将SL0算法应用到块稀疏信号的重构问题中［11］，定义：

由于块稀疏信号重构问题可以转化为如下的优化问题：

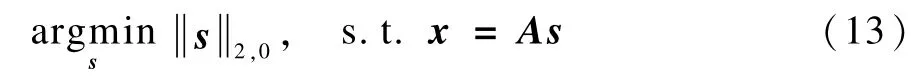
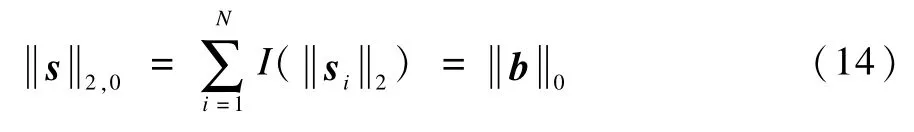
其中，b=［b1，b2，…，bn］T，取反正切函数，可以得到：

于是式（13）转化为如下的优化问题：

式（16）的目标函数是一个凸函数，可以通过梯度下降法求得它的最值。令Δσ表示函数Hσ（s）的梯度，考虑到源信号s的块稀疏特性，Hσ（s）的梯度可以用如下的分块形式表示：

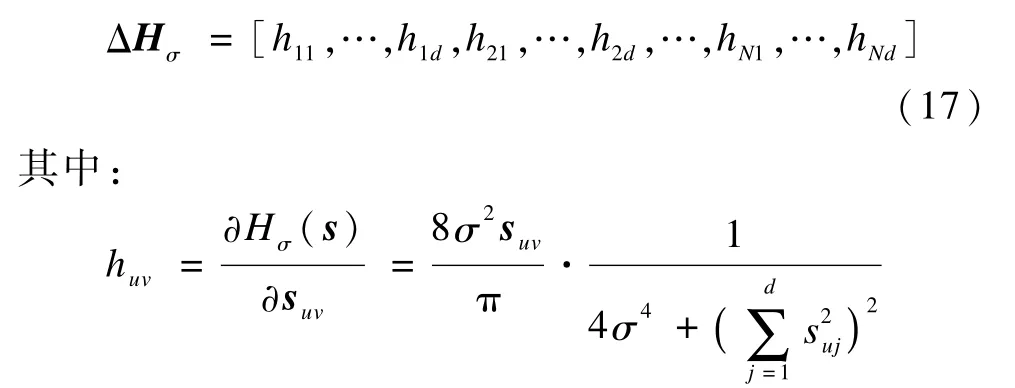
由于σ的取值对Hσ（s）的取值和平滑度有很大影响：σ越大，Hσ越平滑，但是与l0范数的近似程度越差；σ越小，Hσ越不平滑，但是与l0范数越近似。为此，在σ迭代下降的过程中，设置新的动态σ，使得σ在Hσ（s）接近真值时逐渐变小，减慢了速度，但是提高了精度，新的算法在信噪比和重构时间上取到平衡，重构时间上稍作牺牲，却在重构精度上优化效果显著。

具体算法流程如下：

Step1 初始化

（2）选择合适值σ1，σmin，c，cmax，ρ，L，μ。

Step2 for j=1，2，…，J

（1）σ=σj，当σ＞σmin时；

（2）在可行域上使用最速下降算法最小化函数Hσ（s）（其次是投影到可行集）：

2）for l=1，2，…，L（循环L次）

①令ΔHσ如式（6）所示；

②s←s-（μσ2）ΔHσ，其中μ较为较小的整数；

③将s投影到可行集S：

s←s-AT（AAT）-1（As-x）

（3）σ=cσ；

（4）如果c＞cmax，则c=cmax；否则，c=ρc。

算法说明：

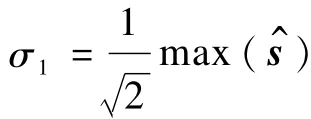
（2）算法Step2的（1）～（4）的作用在于σ迭代下降的过程中，设置新的动态σ，使得σ在Hσ（s）接近真值时逐渐变小，进而提高估计精度。在仿真实验中，取cmax=0.8，ρ=1.2。

4 仿真实验与结果分析

利用蒙特卡罗实验将IBSL0算法与BSL0算法、BOMP算法以及SL0算法进行比较，所有仿真结果都是在W indow s XP操作系统、内存2.00 GB，处理器Intel（R）Core（TM）2 CPU 2.80 GHz，软件M atlab 7.1平台上进行仿真的。

块稀疏信号是人工产生的，方法如下：块稀疏信号为m维向量，将其均匀分成N块，每块大小为d，在N个块中任意选取k块作为非零块，其中每个元素服从均值为0方差为1的标准正态分布N（0，1），其余N-k块所有元素均为0。混合矩阵A∈Rn×m服从均值为0方差为1的标准正态分布，且每列进行单位化。块稀疏信号模型可以表示为：

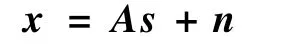
在以下实验中，取源信号维数m=1 000，观测信号维数n=400，内循环迭代次数L=3，μ=2，σmin= 0.000 1。用信噪比（Signal to Noise Ratio，SNR）sSNR来评价估计效果，SNR定义为：

实验1 考查分块大小d变化时，IBSL0算法在不同噪声方差情况下的信噪比变化情况。块稀疏信号的稀疏度为k（即N块中至多k块非零，源信号的整体稀疏度为k×d），改变k和d（块大小）的取值，分为以下2种情况：

（1）k×d=100，（k，d）的取值分别为（100，1），（50，2），（25，4），（20，5），（10，10），（5，20），（2，50），（4，25），（1，100）。

（2）k×d=200，（k，d）的取值分别为（200，1），（100，2），（50，4），（40，5），（25，8），（20，10），（10，20），（8，25），（5，40），（2，100），（1，200）。

图1、图2分别对应k×d=100，k×d=200=n/2（即源信号的总体稀疏度达到观测信号维数的一半），分块从小变大时，IBSL0算法在噪声方差逐渐变大时的信噪比变化情况。可以看出，IBSL0算法的信噪比随着噪声方差变大慢慢降低，当且块大小为20时，IBSL0算法的信噪比约为35 dB，总体来说具有不错的抗噪性能，特别是当k×d=时，IBSL0算法仍然具有不错的估计效果。

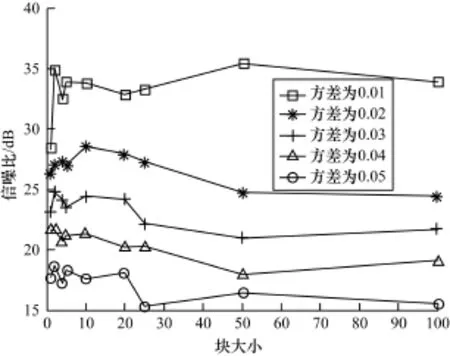
图1 噪声方差变大时IBSL0算法估计性能1

图2 噪声方差变大时IBSL0算法估计性能2

实验2 考查块大小d变化时，IBSL0算法与BSL0算法、BOMP算法以及SL0算法的信噪比变化情况，该实验重复进行50次（每次实验中参数相同，但混合矩阵A及块稀疏信号都随机产生），然后取平均，噪声方差取。

由图3可以看到，当k×d=100时，4种算法都随着分块大小变大时效果越来越好，IBSL0算法与BSL0算法性能相当，但明显好于BOMP算法以及SL0算法，SL0的效果最差。由于当源信号的稀疏度不超过观测信号维数的一半时，式（1）对应的稀疏解s是唯一的，事实上许多算法在源信号的稀疏度达到临界值时都不能很好地恢复源信号s。然而，图4表明，当k×d=200=n/2时，随着分块大小d增大，BOMP算法以及SL0算法信噪比只有10 dB不到，它们几乎不能恢复出原信号，而IBSL0算法信噪比仍然可以达到35 dB，高于BSL0算法信噪比30 dB，可见IBSL0算法相比其他算法具有很大的优势。

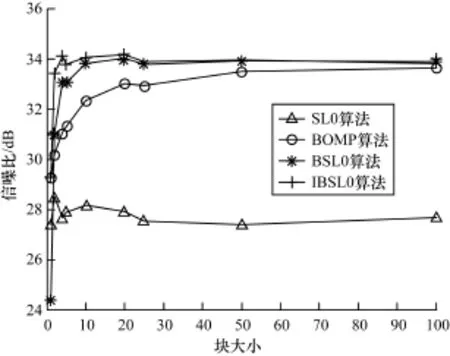
图3 k×d=100时算法性能比较

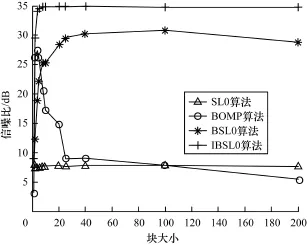
图4 k×d=200时算法性能比较

5 结束语

本文在块稀疏光滑l0范数（BSL0）算法的基础上，用反正切函数替代高斯函数，并对下降因子进行改进，提出了针对块稀疏信号的改进块光滑l0范数（IBSL0）算法。数值实验表明，IBSL0算法不仅具有不错的鲁棒性，而且相比BSL0算法、SL0算法，以及OMP算法，在不同的分块大小情况下，信噪比都有一定的提高，特别是，当源信号的稀疏度达到观测信号维数的一半时（即k×d=），IBSL0算法仍然具有不错的估计性能。然而，本文没有从理论上证明IBSL0算法是否能精确重构，今后的工作主要包括2个方面：（1）给出IBSL0精确的重构条件；（2）进一步研究在块稀疏度或者观测值增加的情况下，该算法与其他算法的重构成功率、运行时间及信噪比的比较。

［1］ Candes E.An Introduction to Compressive Sampling［J］. IEEE Signal Processing Magazine，2008，25（2）：21-30.

［2］ Chen Shaobing，Donoho D L，Saunders M A.Atomic Decomposition by Basis Pursuit［J］.SIAM Journal on Scientific Computing，1999，20（1）：33-61.

［3］ Tropp JA，Gilbert A C.Signal Recovery from Random Measurements via Orthogonal Matching Pursuit［J］.IEEE Transactions on Information Theory，2007，53（12）：4655-4666.

［4］ Dai Wei，Milenkovic O.Subspace Pursuit for Compressive Sensing Signal Reconstruction［J］.IEEE Transactions on Information Theory，2009，55（5）：2230-2249.

［5］ Mohimani H，Babaie-Zadeh M，Jutten C.A Fast Approach for Over-complete Sparse Decomposition Based on Smoothed l0Norm［J］.IEEE Transactions on Signal Processing，2009，57（1）：289-301.

［6］ Stojnic M，Parversh F，Hassibi B.On the Reconstruction of B lock-sparse Signals with an Optional Number of Measure-ments［J］.IEEE Transactions on Signal Processing，2009，57（8）：3075-3085.

［7］ Eldar Y C，Kuppinger P，Bolcskei H.Compressed Sensing of Block-sparse Signals：Uncertainty Relations and Efficient Recovery［J］.IEEE Transactions on Signal Processing，2010，58（6）：3042-3054.

［8］ Wang Yao，Wang Jianjun，Xu Zongben.On Recovery of Block-sparse Signals via Mixed l2/lq（0＜q≤1）Norm Minimization［J］.EURASIP Journal on Advances in Signal Processing，2013，76（1）：1-17.

［9］ 付 宁，曹离然，彭喜元.基于子空间的块稀疏信号压缩感知重构算法［J］.电子学报，2011，39（10）：2339-2342.

［10］ 田鹏武，康荣宗，于宏毅.非均匀块稀疏信号的压缩采样与盲重构算法［J］.电子与信息学报，2013，35（2）：445-450.

［11］ Ham idi-Ghalehjegh S，Babaie-Zadeh M，Jutten C.Fast Block-sparse Decomposition Based on SL0［C］// Proceedings of the 9th International Conference on Latent Variable Analysis and Signal Separation.Berlin，Germ any：Springer，2010：426-433.

［12］ EldarY，Mishali M.Robust Recovery of Signals from a Structured Union of Subspaces［J］.IEEE Transactions on Information Theory，2009，55（11）：5302-5316.

编辑顾逸斐

Block Sparse Signal Reconstruction Algorithm Based on Improved Smoothed l0Norm

QI Rui1a，2，LI Hongwei1b，ZHANG Yujie1b
（1a.Institute of Geophysics and Geomatics；1b.School of Mathematics and Physics，China University of Geosciences，Wuhan 430074，China；2.School of Science，Naval University of Engineering，Wuhan 430033，China）

Smoothed l0norm（SL0）algorithm utilizes a sequence of smoothed Gaussian function with parameter to approximate the l0norm，which can be used efficiently for the compressive sensing reconstruction.Block-sparse signal is a typical sparse signal whose non-zero coefficients occur in a few blocks.This paper proposes a block sparse signal reconstruction based on improved SL0 algorithm with respect to the block sparse signals.The smoothed Gaussian function is substituted by inverse tangent function，and the convergence equality is further improved by optimizing the decreasing factor.Simulation results show that，compared with Block Smoothed l0Norm（BSL0）algorithm，Smoothed l0Norm（SL0）algorithm，and Orthogonal Matching Pursuit（OMP）algorithm，the proposed method has better robustness and higher Signal to Noise Ratio（SNR）.

compressive sensing；block-sparse；Smoothed l0Norm（SL0）；signal reconstruction

祁 锐，李宏伟，张玉洁.基于改进光滑l0范数的块稀疏信号重构算法［J］.计算机工程，2015，41（11）：294-298.

英文引用格式：Qi Rui，Li Hongwei，Zhang Yujie.Block Sparse Signal Reconstruction Algorithm Based on Improved Smoothed l0Norm［J］.Computing Engineering，2015，41（11）：294-298.

1000-3428（2015）11-0294-05

A

TN911

10.3969/j.issn.1000-3428.2015.11.050

国家自然科学基金资助项目（61071188）；中央高校基本科研业务费专项基金资助项目（CUGL130247）；海军工程大学青年基金资助项目（HGDQNEQJJ15004）。

祁 锐（1981-），男，讲师、博士研究生，主研方向：盲信号处理，压缩感知；李宏伟，教授、博士；张玉洁，讲师、博士。

2014-10-28

2014-12-21 E-m ail：qqr0425@163.com