考虑成本上涨的多商品流问题

吴国涛，戚铭尧，张 莹，陈 吉

（清华大学 深圳研究生院物流与交通学部，广东 深圳 518055）

0 引言

多商品流问题出现在各个应用领域，如货物配送、信号传输、电力传输等领域。传统的多商品流问题（Multi-Commodity Network Flow，MCNF）描述的是多个商品在服务网络中共享一些弧段的同时也竞争共享弧段的容量［1］，该问题根据目标函数的不同主要分为最小化成本和最大化利润两类。在最大化利润的情况下，一般假设配送到终点的成本不变，但是在实际情况中商品的成本随配送路径的增加而增加，因此传统的多商品流模型不适合一些实际应用场景。通过运输，商品的成本价格都会有一定程度的上涨，上涨的比率称为成本上涨比率。本文研究在传统MCNF的基础上加入成本上涨因素，目的是最大化分销商的利润。考虑成本上涨的MCNF在实际中应用较多，例如在生鲜食品和农产品等分销过程中，分销商需要选择供应地与需求地之间利润最大的运输方案等。

带容量限制的MCNF已经被证明为NP-hard，目前对该类问题的求解算法主要分为启发式算法和精确算法两大类。启发式算法主要有禁忌搜索、邻域搜索等：文献［2］针对带容量限制的多商品流问题提出一种多层次合作的禁忌搜索算法，通过算例测试发现该算法适合商品数量较大的大规模MCNF；文献［3］针对考虑固定费用的容量限制MCNF，提出一种基于环路的邻域结构，实验表明基于该邻域结构的禁忌搜索算法比其他启发式算法有更好的效果；文献［4］针对整车物流网络规划问题，提出一种流预测与遗传算法相结合的算法，实验表明该算法可以很好地解决整车网络规划问题；文献［5］针对企业分销网络设计问题，提出0-1和优先权混合编码的遗传算法，很好地解决了分销网络设计问题；文献［6］用二阶段优化方法解决了B2C模式下城市配送物流的网络选址问题。一般的MCNP 规模都比较大，精确算法主要集中在分解或列生成算法等：文献［7］针对通信领域的一些附加约束，建立了针对该领域的多商品流模型，并提出对应的列生成算法，测试结果表明该算法可以很好地解决通信领域的多商品流问题；文献［8］针对MCNP提出一种内点算法，以克服传统内点算法求解效率低的缺陷，得到了很好的效率；文献［9］运用三阶段分解算法解决了大规模货物运输问题。列生成算法在大规模线性规划或整数规划方面都表现出很大的潜力，具体见文献［10-11］。

1 模型建立

1.1 问题描述

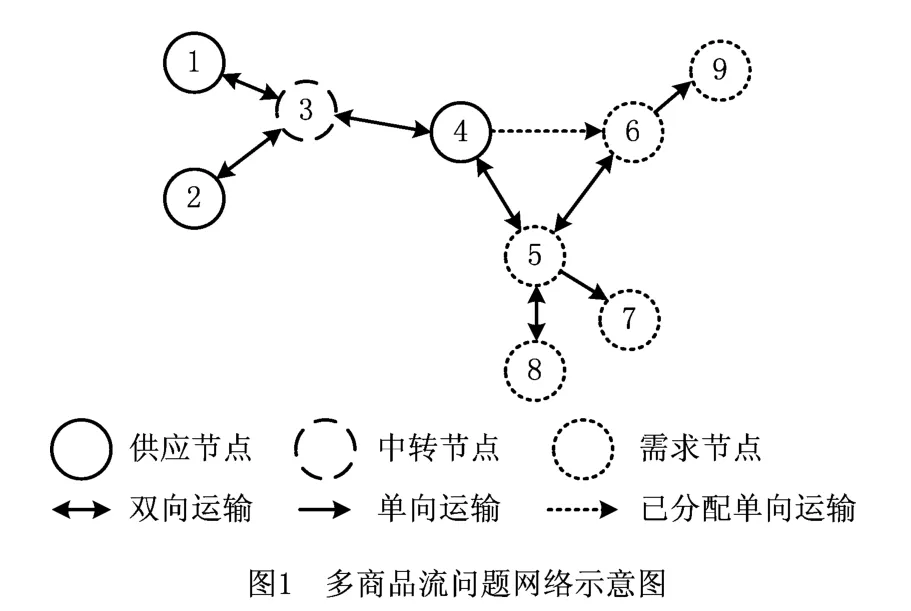
考虑成本上涨的MCNP 可描述为：假设G=（N，A）为一个运输服务网络，N为节点集合，A为有向弧段集合，如图1所示。对于所有的节点，按照运输目的划分为供应节点、需求节点和中转节点三类，其中：①供应节点提供货物，如图1中的节点1，2，4；②需求节点对货物有一定的需求，如图1中的节点5～9；③每一个节点都是一个中转节点，所有货物都可以在中转节点中转，因此供应、需求节点也是中转节点，除此之外还有一类中转节点，只有中转作用，既不提供货量也没有需求，如图1 中的节点3。商品定义为从供应节点到需求节点的供应货量，即每一个商品对应一个供应节点、需求节点和货量。每个商品都需要从供应节点开始，经过一定的中间节点最后达到需求节点，来满足需求节点的需求货量。每个商品的需求节点对应零售价格，供应节点对应基础成本价格。商品的成本价格沿配送路径逐步增加，每通过一弧段，成本价格都按成本上涨比率增加。商品的零售价格与其到达需求节点的成本价格的差值即为该商品的利润。另外，有弧段连接的两节点之间可以运输货物，但是有一定的容量限制。弧段集合A有双向弧段（如图1中节点1到节点3的弧段），表示可以双向运输，也有单向弧段（如图1中节点6到节点9的弧段），表示只能单向运输，除此之外还有一些弧段事先已经存在一定的运输量（如图1节点4到节点6的弧段），表示该弧段安排的运输量至少比已经安排的货量大，但是不超过该弧段的容量限制。在给定运输网络结构和商品需求的情况下，需要设计相应的配送路径，使分销商的利润最大。

1.2 非线性数学模型

为方便讨论，引入以下符号：K表示所有的商品集合；Rk表示第k个商品的所有路径集合；o（k）表示第k个商品的起点；d（k）表示第k个商品的终点；uij表示弧段（i，j）上的最大运输量；pij表示弧段（i，j）的成本上涨率；表示第k个商品第r条路径在弧段（i，j）上的运输量；如果第k个商品第r条路径在弧段（i，j）上有运输量，则，否则；dj表示第j个需求节点的需求量；si表示 第i个供应节点的供应量；aij表示弧段（i，j）的预分配量；demand表示需求节点集合；supply表示供应节点集合；assign表示预分配弧段集合。

考虑成本上涨MCNP的非线性模型如下：

2 列生成算法的设计

高次非线性规划的问题一直没有通用的求解算法。一般来说，小规模问题可以用LocalSolver等非线性求解器求解，大规模问题则采用线性化手段将其转化成线性规划问题或者直接用启发式算法求解。对于考虑成本上涨的多商品流问题，一般都希望得到最优解，一方面最大化其利润，另一方面根据市场实时调整自己的零售价格。因此，本文未用启发式算法而采用降低次数的手段，首先将高次非线性问题分解为主问题和二次非线性子问题，然后设计列生成算法迭代求解从而得到最优解。其中具体线性规划问题用Gurobi优化求解器计算。

列生成算法的基本流程：

步骤1 对于每个商品，求解从其供应节点到需求节点的考虑成本上涨的最短路问题，得到各自的最短路，从而形成初始运输方案，该方案有可能不是可行解，因为可能不满足预分配约束。

步骤2 求解主问题模型，得到当前的最优解及相应的对偶变量。

步骤3 每个商品根据主问题得到的对偶变量，求解对应的最大化检验数模型。如果有商品的最大检验数大于0，则添加相应的新路径和新变量，返回步骤2。

步骤4 输出主问题，得到最优解。

除此之外，由于一般列生成算法的效率比较低，还需要设计加速策略来提高列生成的效率，例如在初始解求解时剔除那些不可能的配送情况，用Gurobi的动态生成新变量功能来提高求解效率等。

2.1 初始解阶段

为了提高列生成的求解效率、使算法尽快得到最优解，在初始解阶段不采用人工变量的方法，而是设计相应的优化模型以获得最有可能存在于最优方案中的路径。对于第k个商品，存在一条路径，使得从供应节点到需求节点的成本价格最小，从而使货物运输商获得的利润最大，因此该路径最有可能存在于整体最优方案中，用它来产生初始解。

获得每个商品最短路径的具体步骤如下：

1）构建每个商品的考虑成本上涨的最短路模型；

2）消除存在的冗余圈。

对于非线性模型中的高次函数表达式，通过引入节点价格变量将其降低为二次函数表达式。对于第k个商品，只有一条成本价格最小的路径。假设弧段（i，j）在该路径上，则节点j的价格变量

式（9）表明，节点j的成本价格为节点i的成本价格与成本上涨率之乘积。通过引入节点价格变量，可以将高次函数表达式转化为二次函数表达式，从而降低求解难度。

第k个商品的考虑成本上涨的最短路模型如下：

其中：目标函数（10）为最小化到达需求节点的成本价格；约束（11）为起始节点的网络约束；约束（12）为中间节点的网络约束；约束（13）为终止节点的网络约束；约束（14）为中间节点的成本价格约束；约束（15）为起点成本的价格需求；约束（16）是为了防止出现自循环约束，加上该约束可以提高算法的效率；约束（17）为变量取值约束。

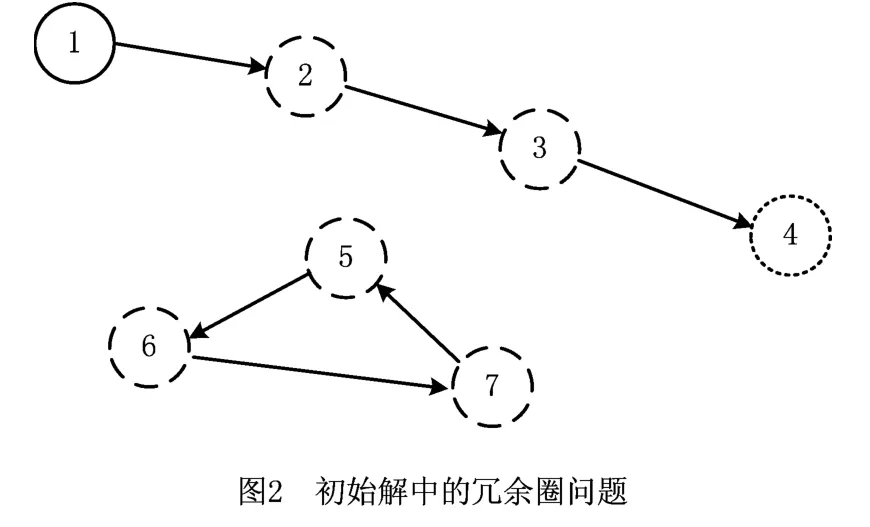
上述模型会出现冗余圈的情况（如图2）。假设节点1为供应节点、节点4为需求节点，则生成的路径中可能会出现与路径完全没有交集的冗余圈（如节点5～7），该冗余圈不会影响传入需求节点的成本价格，但是会对主问题的求解造成很大的影响。为了消除冗余圈，在目标函数中引入对弧段数量的统计，使结果中的弧段越少越好；同时为了减少该统计量对目标函数的影响，应该引入一个微小的统计量。因此将目标函数替换为式（18），其中ε为无穷小量，可取值0.01。

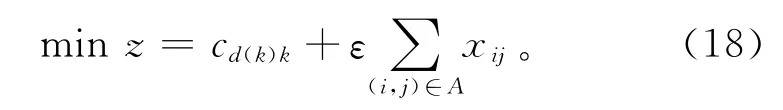
2.2 主问题阶段

根据初始解阶段得到的可行解设计相应的主问题，来获得当前最优解和对偶变量。由于得到的初始解不一定满足预分配约束，即对某一预分配的弧段来说，通过的货量不能保证都大于预分配值。为了保证问题的可行性，对每一个预分配约束引入一个人工变量yij，同时在目标函数中引入人工变量的惩罚成本，当所有人工变量都为0时，得到的解才是原问题的可行解。

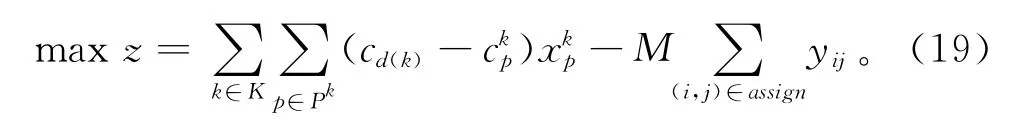
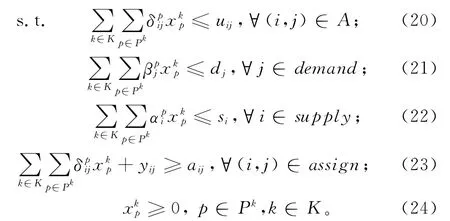
其中：目标函数（19）是最大化分销商的利润和违反预分配约束的惩罚成本之和；约束（20）限制所有经过某弧段的货量不超过其容量；约束（21）限定所有到达某需求节点的货量不超过其需求量；约束（22）限定某供应节点的供应货量不能超过其供应量；约束（23）限制通过某弧段的货量和人工变量之和要超过其预分配量；约束（24）为变量取值约束。

2.3 子问题阶段

子问题主要有两方面作用：①判断主问题得到的解是否为原问题的最优解；②如果没有得到最优解，则向主问题中添加新变量和新路径，使主问题的目标函数值增加。根据主问题得到的对偶变量，对每个商品构建一个优化模型，判断该商品的所有可行路径中是否存在一条路径，使得主问题中加入该路径后其总目标值可以增加，如果存在则将该路径作为新的变量加入主问题中。可以看出问题是一个最大化回路问题，对比初始阶段的模型，唯一不同的就是目标函数：初始阶段的模型是最小化需求节点的成本价格，子问题的目标函数是最大化每个商品对应的检验数。如果对偶变量π=（π1，π2，π3，π4）分别对 应主问题中的四个约束集，则该检验数的表达式为

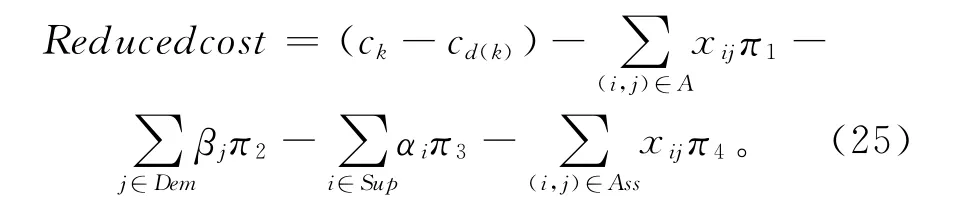
以式（25）为目标函数、以式（11）～式（17）为约束条件和变量取值约束，即为子问题的优化模型。然而该模型得到的最优解同样存在冗余圈问题（如图2），对主问题的求解造成很大的影响。由于子问题的目标函数中包含对弧段的统计，不能用类似初始解阶段的方法。为了消除冗余圈，根据切平面的思想设计相应的破圈约束。这种破圈约束有很多个，为了提高算法的求解效率，采用动态添加破圈约束的方式，具体方法为：当在子问题求解过程中回调函数发现存在冗余圈时，动态添加相应的破圈约束。假设X=｛x1，x2，…，xn｝为路径中存在的冗余圈，对应的冗余圈消除约束为

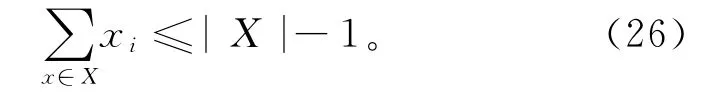
2.4 加速策略

对于大规模的MCNF，传统的列生成算法存在求解效率低下的问题，因此设计相应的加速策略来提高列生成算法的求解效率。加速策略如下：

（1）尽早剔除不可能的商品

由于列生成算法求解效率与商品数量存在正相关的关系，商品数量越大，求解时间就越多，如果能尽早识别那些不可能存在于最优方案中的商品，就可以加快算法的求解。因此可根据初始阶段得到的成本价格最小路径来剔除那些不可能的方案，即如果到达需求节点的成本价格大于需求节点的售价，则该商品绝对不会存在于最优方案中，因为这种商品对货物运输商来说是不盈利的，应该尽早剔除。

（2）利用Gurobi动态添加新变量的功能

列生成算法需要根据子问题的求解结果向主问题添加新的变量。在求解过程中，子问题需要求解很多次，如果重复新建子问题模型，则时间成本太大。采用Gurobi求解器提供的动态添加变量的功能可以消除重复新建模型的消耗，还可以保存之前模型的最优解结构，加速Gurobi求解器的再次求解。

3 算例结果

因为该问题缺少基准数据，所以在算法性能的分析上采用随机生成的测试算例。在实际算例（算例8）的基础上随机增加或减少弧段，通过弧段容量随机生成当前最大最小容量之间的数值并获取10组不同的测试算例，分别对应小、中、大规模算例。算例之间的主要区别为网络规模和商品数量。列生成算法采用C＃语言在VS 2010平台上编程实现，线性模型采用Gurobi 6.0求解器进行求解。算法在处理器为双核Pentium T4300（主频为2.1 GHz）、内存为4GB 的PC 机上运行。表1所示为不同算例的测试结果。

表1 不同算例的结果

表1表明，列生成算法可以很好地解决考虑成本上涨的多商品流问题，而且求解效率比较高。对于小规模问题，算法可以在1s内得到最优解；对于中等规模问题，算法可以在30s内得到最优解；对于大规模问题（算例10），网络规模和商品数都远远大于其他算例，算法可在几分钟内得到最优解。算例表明所设计的列生成算法可以高效地求解该问题。

另外，算例1～3和算例4～9对应着相同网络规模、不同商品数的算例，从运行时间可以看出，在同等网络规模下，商品数越多，算法的求解时间就越长；算例1和算例4（2和5，3和6）对应不同网络规模、相同商品数的算例，结果表明：在相同商品数的情况下，网络规模越大，算法的运行时间就越长。通过对比算例1和算例3（4和6）后发现，在相同网络规模下，商品数增加1倍，算法的求解时间增加3～5倍；通过对比算例1和算例4（2和5，3和6）后发现，在相同的商品数下，网络规模增加1倍，算法的求解时间增加6～13倍。因此，相对于商品数，网络规模对算法的性能影响更大。

表2所示为算例8 的计算结果。算例8 有23个网络节点、56个弧段、4个预分配弧段和104个商品，通过列生成算法得到问题最优解，即17条商品的配送路径和相对应的配送量。

表2 算例5的计算结果

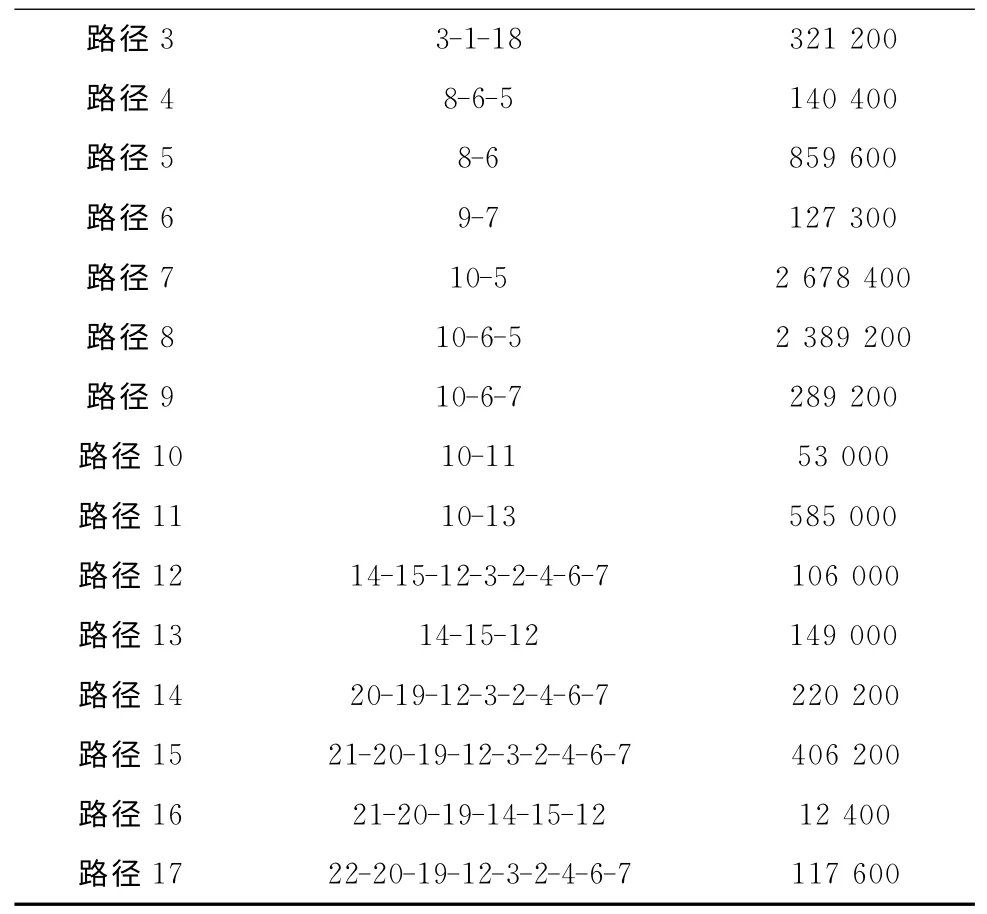
续表2

4 结束语

本文在传统的多商品流问题中引入成本上涨因素，建立了基于弧段的非线性模型，并提出列生成算法，为求解大规模的此类问题提供了一种新的方法。为了加快算法的求解效率，采用了成本价格最小化模型及尽早删除无意义商品的策略；为了消除冗余圈，对初始化模型和子问题模型设计了不同的消除冗余圈方法。测试结果表明，所设计的列生成算法在解决考虑成本上涨的多商品流问题时具有很大的潜力。后续研究可以在多商品流问题中考虑更多的约束，如时效要求等。

［1］JONES K，LUSTIG I，FARVOLDEN J，et al.Multi-commodity network flows：the impact of formulation on decomposition［J］.Mathematical Programming，1993，62（1-3）：95-117.

［2］CRAINIC T G，LI Y，TOULOUSE M.A first multilevel co-operative algorithm for capacitated multi-commodity network design［J］.Computers &Operations Research，2006，33（9）：2602-2622.

［3］GHAMLOUCHE I，CRAINIC T G，GENDREAU M.Cyclebased neighborhoods for fixed-charge capacitated Multi-commodity network design［J］.Operations Research，2003，51（4）：655-667.

［4］QIN Xuwei，FAN Yushun，YIN Chaowan.Research on integrated optimization for automobile logistics network design［J］.Computer Integrated Manufacturing Systems，2006，12（3）：364-370（in Chinese）.［秦绪伟，范玉顺，尹朝万.整车物流网络规划集成优化模型研究［J］.计算机集成制造系统，2006，12（3）：364-370.］

［5］LI Yu，ZHAO Jun，WU Gang.Model and algorithm for location-distribution problem in two-stage distribution network［J］.Computer Integrated Manufacturing Systems，2012，18（11）：2546-2553（in Chinese）.［李 愈，赵 军，吴 刚.两级分销网络选址—配送问题的模型及算法［J］.计算机集成制造系统，2012，18（11）：2546-2553.］

［6］ZHOU Xiang，XU Maozeng，LYU Qiguang.Two-stage layout optimization model for distribution center and terminal node under B2Cmode［J］.Computer Integrated Manufacturing Systems，2014，20（12）：3140-3149（in Chinese）.［周 翔，许茂增，吕奇光.B2C模式下配送中心与末端节点的两节点布局优化模型［J］.计算机集成制造系统，2014，20（12）：3140-3149.］

［7］HOLMBERG K，YUAN D.A multi-commodity network-flow problem with side constraints on paths solved by column generation［J］.Informs Journal on Computing，2003，15（1）：42-57.

［8］CASTRO J.A specialized interior-point algorithm for multicommodity network flows［J］.SIAM Journal on Optimization，2000，10（3）：852-877.

［9］TEYPAZ N，SCHRENK S，CUNG V.A decomposition scheme for large-scale service network design with asset management［J］.Transportation Research Part E，2010，46（1）：156-170.

［10］LUBBECKE M E，DESROSIERS J.Selected topics in column generation［J］.Operations Research，2005，53（6）：1007-1023.

［11］WILHELM W.A technical review of column generation in integer programming［J］.Optimization and Engineering，2001，2（2）：159-200.