基于分数阶偏微分的离散制造系统检测数据融合算法

左延红，程 桦，张克仁

（1.合肥工业大学 机械与汽车学院，安徽 合肥 230009；2.安徽建筑大学 机电工程学院，安徽 合肥 230601；3.安徽大学 资源与环境工程学院，安徽 合肥 230601）

0 引言

当前，人们对产品的需求日益呈现出多样化和个性化趋势，促使传统的少品种、大批量流水生产模式逐渐向多品种、小批量离散制造模式转变。据统计，离散型制造生产已成为机械工业生产的主体［1］，占机械工业总产值的75%～85%。与传统的集中式生产系统相比，离散制造系统是复杂的系统性工程，要想实现对离散制造过程和制造资源的有效控制，及时获得准确的生产数据是必不可少的前提。由于离散制造系统存在制造信息的不确定性和生产过程的多变性，制造执行系统（Manufacturing Execution System，MES）采集到的数据存在种类的多样性、性质的差异性和时间的滞后性等特点，很难为系统的决策提供可靠的依据。如何消除同类设备在生产中因设备性能和工作环境的不同给生产数据带来的差异性，是离散制造系统实现生产资源合理配置、生产调度优化设计和生产过程实时有效控制所面临的核心问题。

为保证离散制造中MES系统获取数据的准确性和实时性，目前多数MES采用数据融合的方法，消除系统在数据采集过程中由于设备性能（如传感器灵敏度）和工作环境（如传输距离）的不同带来的数据差异性。例如文献［2-4］在融合算法中采用数学计算方法，在数据融合中分别采用模糊集、模糊神经网络等理论，但该算法需要先通过离线训练网络建立模糊逻辑规则和动态模型。文献［5-6］在融合算法中采用概率模型方法，但该算法的融合效果依赖于模型的选取，而确定概率模型受主观因素的影响较大。文献［8］提出的方法中各离散型制造系统均采用自主数据处理的方法，注重单个节点的性能最优化，以至于各节点的数据之间很难有效融合并实现全局最优化。文献［9］提出的算法虽然改进了单个节点的最优化问题，但数据的差异导致离散型制造系统各节点间的物联网检测数据无法实现数据交互和融合。文献［10］提出的算法实现了相互离散制造系统物联网中各节点之间的数据交互和融合，但数据间的差异性严重制约数据间的融合有效度。文献［11-12］解决了数据差异给数据有效度带来的制约，但算法过程复杂，容易产生过多冗余信息，很难实现数据融合。

本文提出基于分数阶偏微分的离散制造系统差异数据融合算法，首先采用物联网技术统一收集离散分布于制造系统各检测终端的生产数据信息，汇总所有信息，然后采用分数阶偏微分算法对所获取的检测数据进行差异化分析与处理，从而实现检测数据的有效融合。限于篇幅，本文只选用某公司离散分布的4个车间中的10台数控车床作为实验对象，采用物联网技术收集各机床主轴箱油温的检测数据，最后使用分数阶偏微分算法对检测数据进行融合处理，测试系统的数据融合性能。

1 基于分数阶偏微分融合算法的数学模型

1.1 分数阶导数定义

分数阶微积分没有严格的定义，由于不同的应用领域可以得到不同的定义，到目前为止，在基本理论和工程应用研究中比较著名的有Grunwald-Letnikov、Riemann-Liouville和Caputo Riesz三种分数阶导数定义［13-14］。

（1）Grunwald-Letnikov定义

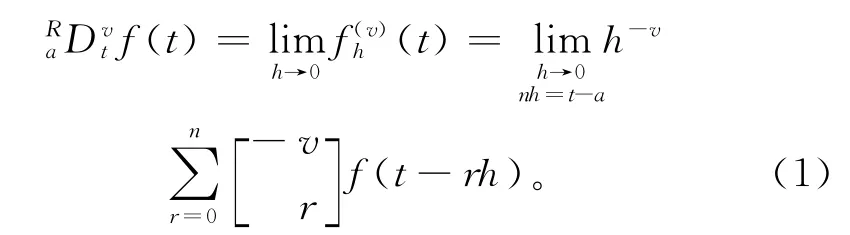
式中0≤n-1＜v＜n。

该定义是从研究连续函数整数阶导数的经典定义出发，将导数的阶数由整数推广到分数演变而来，主要应用于数值计算。

（2）Riemann-Liouville定义

式中0≤n-1＜v＜n。

该定义从分数阶微积分的基本性质出发，对Grunwald-Letnikov定义进行了改进，从而实现计算的简单化。

（3）Caputo定义

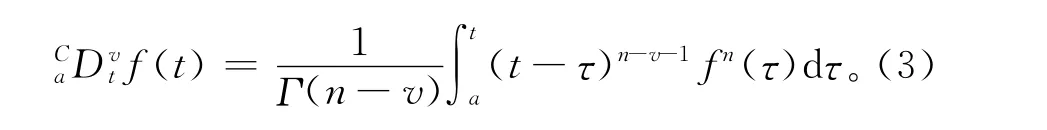
式中0≤n-1＜v＜n。

该定义是对Grunwald-Letnikov定义的另一种改进，由于以上两种导数进行某些变换时会产生一些余项，Caputo 定义可以使一些计算变得更加简洁，易于工程应用。

目前分数阶微积分理论已广泛应用于测量信号的处理中，研究发现：分数阶微分理论可以在增强测量信号的高频部分的同时非线性地保留信号的低频部分，但也在一定程度上加强了信号中的干扰成分。分数阶积分理论在加强检测信号低频部分的同时，部分保留了信号的最低频部分，但阶次的合理选用存在难题，阶次较小时去干扰效果不明显，阶次较大时信号容易出现模糊现象。因此，分数阶微积分理论在处理离散制造检测信号时，很难同时解决检测信号存在的工作环境干扰和远距离传输信号减弱的问题。本文将在检测信号的处理中引入分数阶偏微分理论，探讨应用分数阶偏微分理论建立检测信号融合算法模型，并分析基于分数阶偏微分理论的差异性数据融合的效果。

1.2 分数阶偏微分方程

分数阶微积分方程由整数阶偏微分方程演化而来，是用分数阶偏导数代替传统的整数阶偏微分方程中对函数影响因子的偏导数项而得到的。分数阶偏微分方程的基本形式为［15］：

式中：α和β为偏微分阶次；x和y为函数S（x，y，t）数值的影响因子。

近几年，国内外学者经过研究发现，分数阶微积分在信息领域的应用具有广阔的前景，如系统建模、曲线拟合、系统判别、模式识别、系统稳定性分析，特别是在信号的奇异性检测和提取方面具有特殊的作用［15-16］。

本文根据离散制造系统生产数据种类多样、信息量大，数据计算复杂的特点，决定采用Grunwald-Letnikov定义来简化系统数据的计算程序，从而减少系统数据的融合时间，提高MES的工作效率。

1.3 差异性数据融合算法模型

因为BV（Ω）空间建立在传统的梯度模值的基础上，而分数阶微积分的有界变差空间BVv（Ω）建立在传统的BV（Ω）变差空间的基础上，所以BVv（Ω）空间应该建立在分数阶梯度模值的基础上，从而可以用建立基于分数阶有界变差空间BVv（Ω）的能量泛函的方法来描述离散制造系统中的差异化数据信号。

已知离散MES中收集到的生产信息S（x，y），x，y∈Ω，将Rudin，Osher和Fatemi提出的去噪ROF（Rudin-Osher-Fateri）模型［17］的正则项梯度算子DS用分数阶梯度算子DvS代替，可以得到基于分数阶偏微分方程的去差异性数学模型的能量泛函：

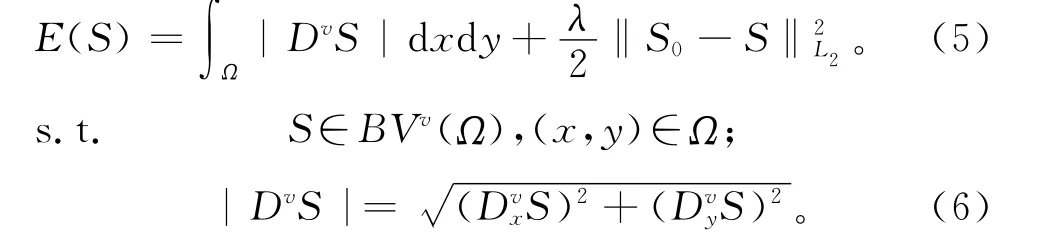
假设影响因子x、y对S（x，y）相互独立，因此只需考虑在x影响因子作用下的数据信号S（x，·）的分数阶微积分的计算即可。由分数阶微积分的G-L定义，可得生产数据检测信号S（x，·）的分数阶微分为：

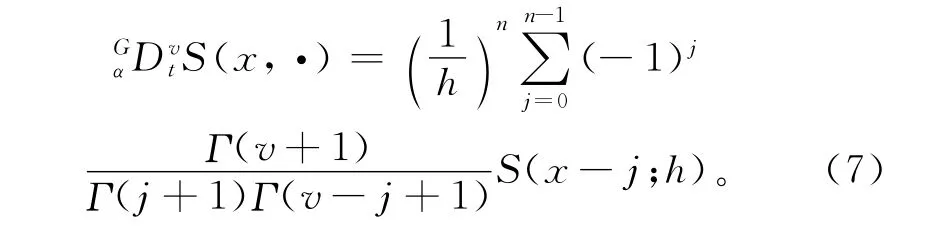
当步长h=1时，可得离散制造系统差异化数据融合系统的目标函数为：

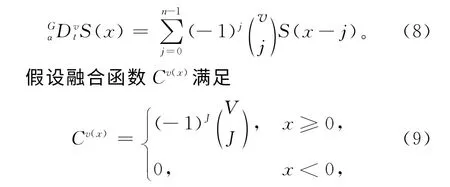
则差异化数据融合系统目标函数可以转化为数据信号S（x）与函数Cv（x）的卷积操作形式：

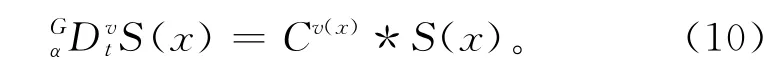
将上式代入基于分数阶BVv（Ω）空间的能量泛函（式（5）），可得基于分数阶微积分的离散MES差异化数据融合模型：

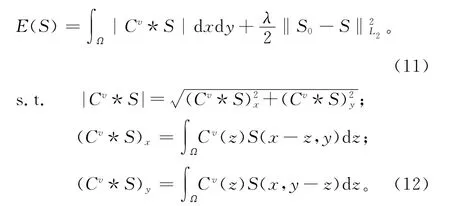
为了得到式（11）的Euler-Lagrange方程，需要对公式进行极小化处理。根据变分法的性质构造相应的能量泛函，假设存在任意函数φ，使其满足

根据泛函极值的基本性质，令g′（0）=0，则可得

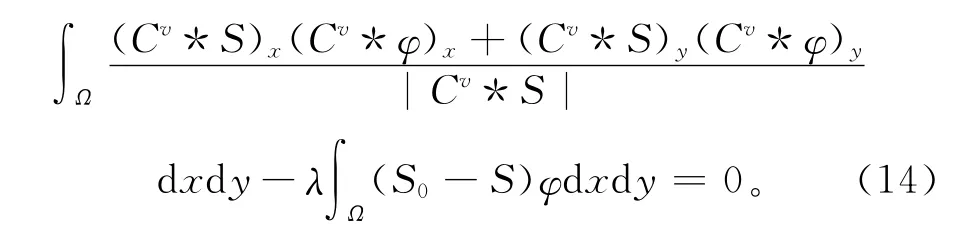
因为当生产数据检测信号影响因子（x，y）∉R时S（x，y）=0，所以当Ω→R2时，消除任意函数φ［18］，可得Parseval恒等式：

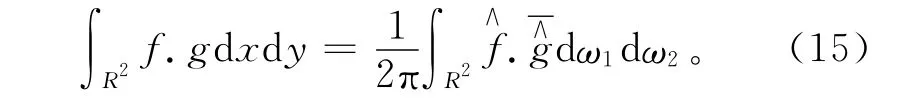
则可以根据Parseval恒等式，将式（14）变换为：

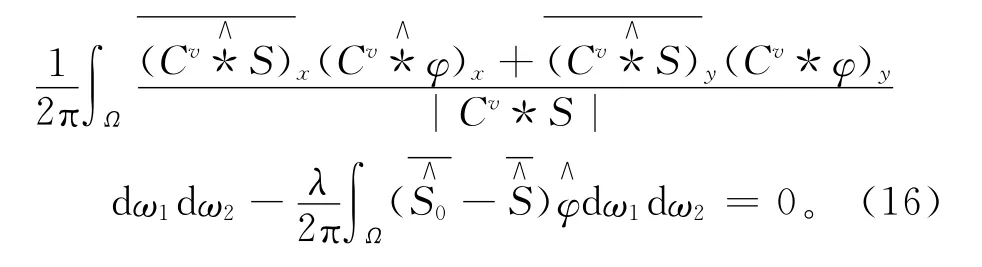
因此，利用梯度下降法，可以得到基于G-L 定义的差异性数据检测信号分数阶偏微分方程的融合算法模型：

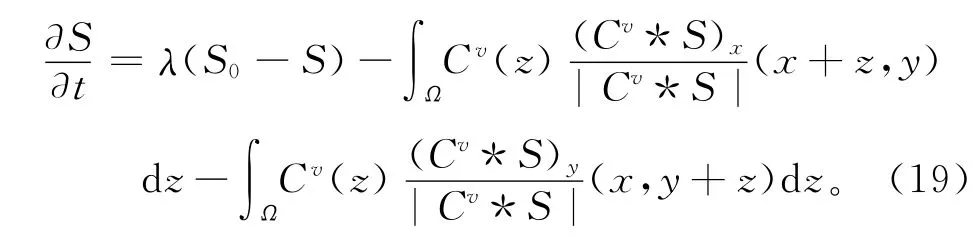
根据信号处理的基本运算性质，将上式进行化解，可得

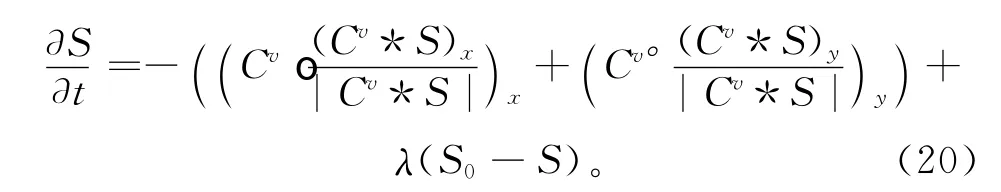
由上式可以看出，基于分数阶偏微分方程的融合算法模型是由分数阶微分算子与差异性数据检测信号进行相关和卷积操作，从而大幅度提高了融合模型的计算速度。

2 离散制造信号特点及其融合过程

2.1 离散制造信号特点

由于离散制造系统是一项复杂的系统工程，制造系统中的设备型号多样、布置分散，不同产品在制造过程中产生的信号数据各不相同，使系统检测到的信号存在较大差异。研究发现，通过物联网收集到的设备检测信号数值主要受内在因素和外在因素的影响。内在因素如设备的使用性能、检测仪器的分辨率等，直接影响检测数据的数值与精度；外在因素包括设备所处的工作环境和设备在信号传输距离等，直接给检测信号带来干扰和能量损耗。不准确的检测信息直接影响制造系统工作的可行性和可靠性，这是目前离散制造系统面临的一大难题［19］。

为减小因上述原因给离散制造系统中的同类检测数据带来的差异性，多数MES在数据处理时采用数据融合算法，如概率模型方法、矩阵特征向量的稳定理论法、最小二乘法、平均值法等，这些算法在数据的融合过程中各有所长，但是对于减小数据的差异性还是不太理想，本文拟应用分数阶偏微分方程理论对检测数据的差异性进行融合处理。

2.2 基于分数阶偏微分理论的差异性数据融合方法

为有效控制与管理制造系统，MES通过物联网收集检测网络所有节点的检测信号数据，采用分布式系统下的积分思想［9-10］，将所收集的数据进行分类，对各类数据间的差异性进行评判，如果数据的差异性超过系统设定的公差范围，则采用分数阶偏微分算法对数据进行处理，最终实现差异性数据的高效融合。

数据融合的基本步骤如下：

步骤1 收集检测网络各节点检测数据，并将其进行分类，判断同类检测数据间的误差是否在系统设定的范围内。

步骤2 根据各节点的多个测量值，计算影响该节点测量值的内在影响因子xi；根据各区域所有节点的测量值，计算该区域节点测量值的外在影响因子yi值。

步骤3 综合所有测量值，运用MATLAB 软件拟合出数据测量值S（x，y）的方程。

步骤4 参考式（20），构建方程S（x，y）的基于分数阶偏微分方程的差异数据融合模型。

步骤5 运用数据融合模型融合各检测节点的测量值，评价融合效果，如融合后的数据误差在系统设置的范围内，则向数据中心输送融合后的数据。

如上所述，离散MES 通过物联网安装在各制造资源上的数据终端收集各类制造信息数据，由于各制造设备的性能、数据终端检测仪器的分辨率和工作环境存在较大差异，使得物联网收集的信息数值也存在较大差异，很难为MES提供可靠的信息，因此融合离散制造系统的生产数据差异性是实现MES可靠性的前提。

基于分数阶微积分的数据处理技术是一门崭新的交叉学科分支，它融合了数学、物理学、电子信息学和计算机科学等多个领域的理论知识。分数阶微积分在现代工程分析与计算特别是在化学、电磁学、材料学和力学等学科中得到广泛应用和关注，并取得了可喜的科研成果。然而，如何将分数阶微积分用于现代信号的分析与处理，国内外还很少有人涉足。一方面是因为整数阶微积分已经广泛应用于传统的信号分析与处理技术中，另一方面是因为现代信号分析与处理的研究主要集中于研究信号的非线性、非因果性、非最小相位系统和非整数（分形）信号等领域。本文尝试将分数阶微积分理论应用于信号数据的差异性融合，打破传统的用整数阶微积分处理信号数据的方法，通过设定一个较小的分数微积分来构建数据融合模型，并利用迭代法来控制数据融合的效果。

3 仿真实验与分析

3.1 实验环境描述

为检验分数阶偏微分方程对于离散制造系统生产数据融合的效果，通过物联网技术收集分布于4个生产车间10台数控车床的主轴箱油温检测数据，其中甲车间数控车床3 台、乙车间2 台、丙车间2台、丁车间3台，4个生产车间与数据采集中心的距离存在较大差异，各机床和温度传感器的性能参数相近，但设备折旧率各不相同。由于存在传输误差、环境噪声、人为干扰、传感器自身的精度及机床自身性质等因素的差异性，测量数据将不严格服从正态分布。实验时，10台机床同时工作，生产任务基本相同，测温仪同时启动，且以每10秒钟采样1次的频率开始工作。在实际工作中，温度测量值的影响因子（xi，yi）和拟合方程S（x，y）随着采样数据的增加而更加精确，由于篇幅有限，本实验只取机床连续工作1h后1 min内的60个采样数据作为分析样本，设第i台车床的第j次测量值为Cij，采样数据如表1所示。

表1 离散分布数控车床主轴箱油温测量值Cij ℃

为了直观地显示各机床主轴箱油温测量值的特点，寻求测量值与设备仪器性能和环境因素之间的关系。求得各测量点温度的平均值分别为53.447℃，53.110 ℃，54.282 ℃，53.187 ℃，53.157 ℃，53.235 ℃，54.095 ℃，54.445 ℃，54.178 ℃，53.390 ℃，绘制各机床主轴箱油温示意图如图1所示。

从图1可以看出，各机床测量值的差异性较大，数据点的离散型较强。其主要原因是仪器设备的性能和数据的传输距离不同。如：与数据采样点近的老旧设备的油温较高，设备老旧且离数据采样点较远和设备较新且离数据采样点较远的油温与平均值较近，设备较新且离采样点较近的油温较低，从而使图1中的数据分为三类：①在平均值线以上且远离平均值线，②在平均值线附近，③在平均值线以下且远离平均值线。采样数据存在如此大的差异，无法给制造系统提供准确的数据信息，从而影响了制造系统对设备管理的可靠性和准确性。

3.2 差异数据融合处理

为获得准确的检测数据，需要减少因设备性能和外在环境对测量值的影响。文献［7］中融合算法的融合结果分别为53.485℃，53.302℃，53.868 ℃，53.263℃，53.215℃，53.154 ℃，53.751 ℃，54.155 ℃，53.827℃，53.532℃。本实验采用基于分数阶偏微分的方法对测量数据进行融合处理，融合过程如下：

（1）用标准温度计测得第i台机床主轴箱的油温，作为其标准测量值，利用机床工作过程中的100个采样值，运用MATLAB 软件求得该机床测量值的内部影响因子xi。再将各车间所有测量值的平均值作为标准测量值，根据10台机床的所有测量值，运用MATLAB软件求得各车间测量值的外部影响因子yi。

（2）由于采集的数据值与传感器的测量值为非线性关系，可用有限项的幂级数构造函数，公式为：

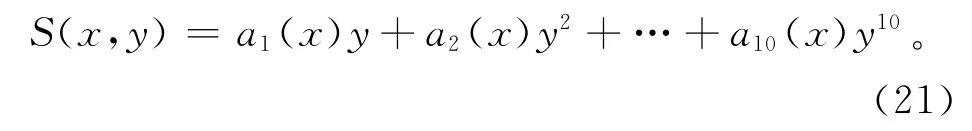
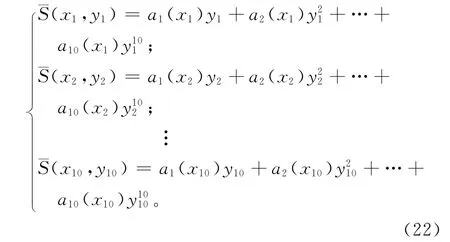
由式（22）可以解得a1，a2，…，a10的值，代入式（21）可得到S（x，y）的方程式。

（3）根据式（20），结合分数阶偏微分方程的Grunwald-Letnikov定义中偏微分次数的取值范围，为了方便计算，本实验取v=1／2，求解基于分数阶偏微分算法的离散制造系统中数控机床主轴箱的油温检测差异性数值融合数学模型。

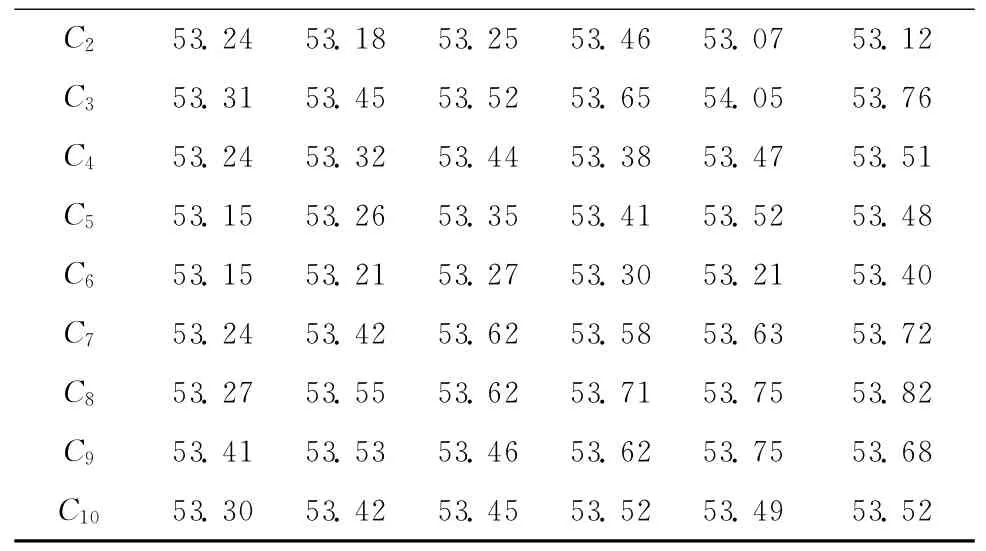
（4）将（1）中的计算结果（xi，yi）代入数据融合模型，即可获取融合后的数据，如表2所示。

表2 融合后数控车床主轴箱油温测量值 ℃

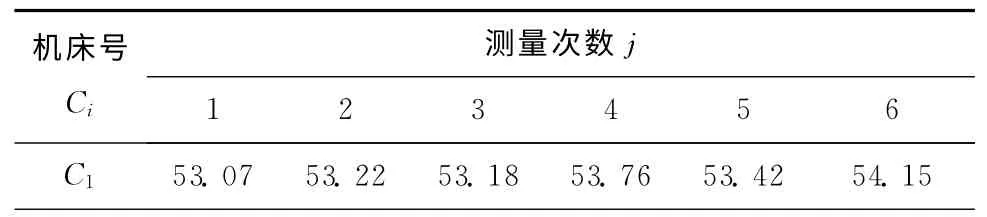
表2 融合后数控车床主轴箱油温测量值 ℃

续表2

由表2的数据可得，经过分数阶偏微分算法融合后各机床所测温度的平均值为53.467 ℃，53.22℃，53.623 ℃，53.393 ℃，53.362 ℃，53.257 ℃，53.535 ℃，53.620 ℃，53.575 ℃，53.45 ℃。综 合以上三种算法，各机床主轴箱温度测量值经不同算法融合处理的数据曲线如图2所示。

从图2可以看出，平均值融合算法数据的离散性在三种算法中最强，经文献［7］中的融合算法处理后，数据的离散性有所减弱，但效果还是不及本文所述的分数阶偏微分算法。三种算法的总绝对误差如表3所示。

表3 三种融合算法总绝对误差比较

实验结果表明，本文算法融合后的数据总绝对误差远小于平均值融合算法和文献［7］中采用的算法，而且融合后数值的波动性较小，融合的精度得到了显著提高。

4 结束语

本文引用分数阶偏微分数据融合算法对检测信号的作用进行了研究分析，提出了基于分数阶偏微分方程的离散制造管理系统差异数据融合算法，利用各生产设备的一组测量数据求出影响测量数据值的内在影响因子xi，利用同一车间同类生产设备的测量值求出影响测量数据值的外在影响因子yi，再利用分数阶偏微分方程建立了生产设备差异性检测数据的融合模型，从而得到融合后各生产设备的测量数据值。本文采用4 个离散分布的生产车间中10台数控车床的主轴箱油温测量值作为实验对象，测试本文算法的融合效果。实验结果表明，采用基于分数阶偏微分方程的差异性数据融合算法，数值总绝对值远小于其他算法，而且数值波动性小、融合精度高，为离散制造系统提供了准确的生产数据，从而提高了管理系统的可靠性。

［1］ZHOU Yanyou，CHEN Changnian.New settlement projects for multiple type，single part，smallbatch production and seldom type，large batch production［J］.Manufacturing Technology &Machine Tool，2007（5）：28-36（in Chinese）.［周延佑，陈长年.多品种、单件、小批量生产和少品种、大批量生产解决方案的新发展［J］.制造技术与机床，2007（5）：28-36.］

［2］LEBLANC K，SAFFIOTTI A.Multi-robot object localization：a fuzzy fusion approach［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2009，39（5）：1259-1276.

［3］GAO Hongyan.A simple multi-sensor data fusion algorithm based on principal component analysis［C］／／Proceedings of the 2009ISECS International Colloguium on CCCM'09.Washington，D.C.，USA：IEEE，2009.

［4］WAN Shuping.Vague set method for multi-sensor information fusion［J］.Computer Engineering，2009，35（12）：259-260，263（in Chinese）.［万树平.多传感器信息融合的Vague集法［J］.计算机工程，2009，35（12）：259-260，263.］

［5］ZHAO Jie，JIANG Jing，ZHOU Yangjing，et al.RLS-based registration algorithm for multi-sensors［J］.Trans-ducer and Microsystem Technologies，2007，26（8）：99-101.

［6］HEDJAZI M H，GHARI M，ABOLMAESUMI P.Distribution of fiducial registration error in rigid-body point-based registration［J］.IEEE Transactions on Medical Imaging，2009，28（11）：1791-1801.

［7］TU Guoping，YE Suping.Algorithm for the sensors data fusion［J］.Journal of Transducer Technology，2003，22（3）：30-32（in Chinese）.［涂国平，叶素萍.一种传感器数据的融合算法［J］.传感器技术，2003，22（3）：30-32.］

［8］HE R，WANG Y J，WANG Q，et al.An improved particle swarm optimization based on self-adaptive escape velocity［J］.Journal of Software，2005，16（12）：2036-2044.

［9］TRELEA I C.The particle swarm optimization algorithm：convergence analysis and parameter selection［J］.Information Processing Letters，2003，85（6）：317-325.

［10］STUTZLE T，HOOS H H.MAX-MIN ant system［J］.Future Generation Computer System，2000，16（8）：889-914.

［11］LIN Dan，LI Minqiang，KOU Jisong.A GA-based method for solving constrained optimization problems［J］.Journal of Software，2001，12（4）：628-632（in Chinese）.［林 丹，李 敏强，寇纪松.基于遗传算法求解约束优化问题的一种算法［J］.软件学报，2001，12（4）：628-632.］

［12］WU Jianping，LIN Song，XU Ke，et al.Advances in evolvable new generation internet architecture［J］.Chinese Journal of Computers，2012，35（4）：203-212（in Chinese）.［吴建平，林嵩，徐 恪，等.可演进的新一代互联网体系结构研究进展［J］.计算机学报，2012，35（4）：203-212.］

［13］OLDHAM K B，SPANIER J.The fractional calculus［M］.New York，N.Y.，USA：Academic Press，1974.

［14］PODLUBNY I.Fractional differential equations［M］／／Mathem-atics in Science and Engineering.Pittsburgh，Pa.，USA：Academic Press，1999.

［15］LIAO Ke.Digital filter design and analog circuit implementation of fractional calculus with its application［D］.Chengdu：Sichuan University，2006（in Chinese）.［廖 科.分数阶微积分运算数字滤波器设计与电路实现及其应用［D］.成都：四川大学，2006.］

［16］TAO Ran，QI Lin，WANG Yue.Theory and applications of the fractional Fourier transform［M］.Beijing：Tsinghua University Press，2004：23-49（in Chinese）.［陶 然，齐 林，王越.分数阶Fourier变换的原理与应用［M］.北京：清华大学出版社，2004：23-49.］

［17］RUDIN L，OSHER S，FATEMI E.Nonlinear total variation based noise removal algorithms［J］.Physica D，1992，60（1／2／3／4）：259-268.

［18］DING Zhiming，GAO Xu.A database cluster system framework for managing massive sensor sampling data in the Internet of Things［J］.Chinese Journal of Computers，2012，35（21）：213-229（in Chinese）.［丁治明，高 需.面向物联网海量传感器采样数据管理的数据库集群系统框架［J］.计算机学报，2012，35（21）：213-229.］

［19］ZUO Yanhong，ZHANG Keren.Discrete data fusion with integral discrete guidance in Internet of things［J］.Computers Science，2014，41（3）：149-152（in Chinese）.［左延红，张克仁.积分离散引导的物联网中离散系统差异数据融合［J］.计算机科学，2014，41（3）：149-152.］