板坯热轧计划编制的优化模型与算法

刘 健，王 彬，王柏琳，2，王 宝，邹草云，刘 青+

（1.北京科技大学 钢铁冶金新技术国家重点实验室，北京 100083；2.北京科技大学 东凌经济管理学院，北京 100083）

0 引言

热轧工序是钢铁生产最后的关键工序，热轧计划需要确定更换轧机的两工辊之间生产的板坯顺序，计划编制的好坏直接影响到板坯的热装率和产品的质量。一个热轧计划内的板坯由烫辊材和主体材两部分组成，其中烫辊材的数量一般为4～8块板坯，依靠人工编制就能够得到较好的结果，而主体材的数量较多，通过人工编制很难获得合理的方案。因此，在热轧计划编制中，笔者只考虑主体材的编制。

近年来，国内外学者对热轧计划编制开展了一定的研究。例如：Kosiba等［1］在研究热轧计划时，将热轧计划归为旅行商问题（Traveling Salesman Problem，TSP），并给出了钢卷宽度、厚度、硬度跳跃的惩罚表；Shu等［2］将热轧批量调度问题配制成一个多目标车辆与双倍时间窗问题，鉴于所提出的模型复杂性和在实际生产中考虑目标的优先级，分解为基础的分层优化算法来求解；Jia等［3］将热轧批量计划归为多目标奖金收集的车辆路径问题（Prize Collecting Vehicle Routing Problem，PCVRP）模型，为避免遇到选择权重系数的单目标优化，运用基于帕累托主导地位的多目标优化算法求解该模型；Tu等［4］将热轧计划归为奖金收集的车辆路径问题模型，该模型考虑温度的跳跃极限和卷取相邻平板的温度以及铸坯表面等级和混合轧制板坯，同时考虑合理安排的热材料和大宗材料；吕志民等［5］为提高热装批量计划的调度可行性，构建了一种集成批量计划类型及部分调度约束的批量计划约束满足模型，并采用显性基因的约束遗传算法进行优化求解；李铁克等［6］考虑面向冷装、温装、热装和直轧等多种生产工艺，建立了问题的约束满足模型；邹宗华等［7］通过研究得出结论：当轧制计划包含两种不同钢种时，不同钢种的板坯重量应大致相同，板坯交替排列；姚筱春等［8］针对1 880 mm 热轧线轧制计划编排进行优化，采用不同钢种进行交叉编排，并根据加热时间确定合适的交叉比，以达到提高轧制计划单重和热送热装水平的目的。

现有的研究成果存在以下不足：

（1）初始数据未考虑多钢种因素尤其不兼容钢种因素，建立热轧计划模型时很少考虑板坯出炉温度的跳跃惩罚值。

（2）运用所选择的算法时参数优选没有详细的分析，导致算法的计算效率和准确度有待提高。

针对上述不足，本文考虑不兼容钢种和出炉温度跳跃因素，使其更贴近实际生产要求，同时采用改进的遗传算法（Genetic Algorithm，GA）即单亲GA求解，探讨算法的基本参数和目标函数的惩罚值，改进算法的求解策略，以使其获得的热轧计划能够在保证可操作性的基础上实现进一步优化。

1 热轧计划的数学模型

在编制热轧计划时，除了考虑主体材的热轧规程外，还通过订单数据和库存数据优化、建立热轧计划数学模型来解决不兼容钢种热轧计划编制问题。另外，根据建立的热轧计划数学模型的特点，将其归结为车辆路径问题（Vehicle Routing Problem，VRP）模型。

1.1 热轧计划编制规程

热轧计划的编制是为了保证热轧计划数和相邻轧制宽度以及硬度和厚度跳跃的总惩罚值最小，在考虑轧制规程的条件下安排每个板坯的热轧顺序。主体材的热轧规程如下［9-11］：

（1）轧制宽度向非增的方向平滑变化；如果遇到同宽钢卷连续轧制，则要求总的轧制长度有一定的上限。

（2）轧制厚度最好是沿着非减的方向平滑变化。

（3）轧制硬度最好是向逐渐减小或增加的方向平滑变化且不允许反复跳跃。

（4）轧制宽度反跳时，跳跃差不能超过150mm。

（5）一个热轧计划内的钢卷总长度不能超过一定的千米数。

（6）一个热轧计划内的轧制宽度、厚度和硬度不能同时变化。

（7）当轧制宽度、硬度和厚度相互冲突时，优先级为硬度—厚度—宽度。

除了以上主体材的热轧规程外，还需要考虑钢厂生产钢种的多样性及特点，否则编制在同一个热轧计划内的钢种可能存在一定的冲突。热轧计划是根据钢厂的订单数据和库存数据编制的，在订单合同提前到位的基础上匹配库存数据，对计划周期内的合同数据和库存数据按品种、规格和轧制工艺进行分析。

例如，某钢厂生产的板坯包括不锈钢和碳钢，因为生产不锈钢的加热制度、轧辊辊系均与碳钢存在很大区别，按照目前的工艺技术水平不能实现碳钢和不锈钢混合轧制，所以要求不锈钢与碳钢分别编制轧制计划，表1针对这一情况给出了不兼容钢种热轧计划编制规程，据此对订单数据和库存数据进行优化。为避免不兼容钢种交叉排产的现象，将订单数据和库存数据中的钢种分为碳钢和不锈钢；对不能交错排产的B、D 和E钢种，集中生产且生产量和库存量满足一个或多个轧制单元；对于多个生产订单钢种规格相同或相近且热轧工艺允许大批量交叉排产的钢种，集中编制热轧计划。

表1 不兼容钢种热轧计划编制规程

因此，在初始数据优化的基础上，依据主体材的热轧规程，构建热轧计划的数学模型。

1.2 模型构建

VRP模型的描述如下：分别处于不同区域的客户有不同的订货需求，每辆车都有一定的载重要求，要求用最少的车辆数来满足不同地域客户的需求，并使总运费最少。若将一个轧制计划等价于一台车辆，板坯视为需要访问的客户，最小化热轧计划数和最小化惩罚值分别对应最少的车辆数和总运费最小，则本文所考虑的热轧计划问题可以归结为一类VRP模型。

根据以上描述，可以建立热轧计划问题的数学模型。首先定义如下参数：板坯i，j∈｛0，1，2，…，n｝，热轧计划k∈｛1，2，…，m｝；n为需要编制计划的板坯数量，其中，i=0 表示构造编号为0 的虚拟板坯，作为车辆路径问题（VRP）的源点，即车辆的中心点；m为热轧计划数；s为n块板坯中的某一块；为板坯i到j的惩罚值，其中分别为板坯i到板坯j的轧制宽度、厚度、硬度、出炉温度和交货期惩罚值，c0i=0，ci0=0，cii=∞，i=0，1，2，…，n；nk为热轧计划内的板坯数量；qi为板坯i的热轧长度；qi1为A钢板坯的热轧长度；Qk为热轧计划k内的板坯长度约束；R为相同轧制宽度板坯的热轧长度约束；Wi为第i块板坯的轧制宽度；Wmax为某热轧单元相邻板坯轧制宽度变化的最大值；Di为第i块板坯的轧制厚度；Dmax为某热轧单元相邻板坯轧制厚度变化的最大值；Hi为第i块板坯的轧制硬度；Hi2为难轧材第i块板坯的轧制硬度；Hmax为某热轧单元相邻板坯轧制硬度变化的最大值；Ti为第i块板坯的出炉温度；Tmax为某热轧单元相邻板坯的出炉温度变化最大值；

对于交货期差异引起的惩罚，定义为

则热轧批量计划的数学模型如下：

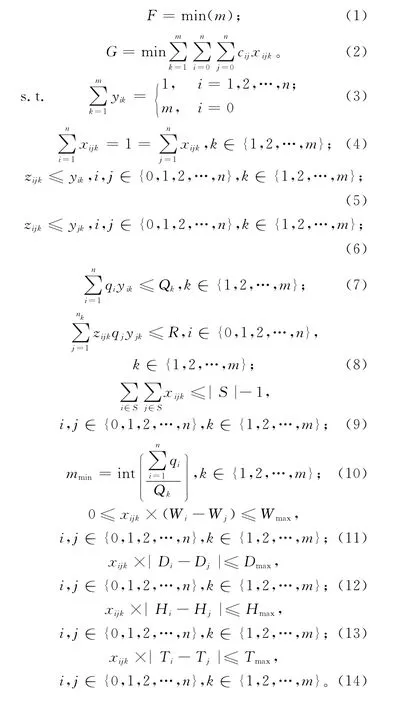
其中：目标函数式（1）为最小化热轧计划数；目标函数式（2）为最小化惩罚值，考虑到相邻板坯之间的出炉温度跳跃值大小会影响到加热炉加热板坯的质量、效率和轧机轧制质量，跳跃值越小，越有利于加热炉和轧机生产，因此本文增加板坯出炉温度跳跃的惩罚值，能够满足出炉温度相同或相近的板坯批量生产；式（3）保证所有板坯必须被分配且仅被分配到某一个热轧计划（除了被所有热轧计划所包括）；式（4）保证每一块板坯只能被处理一次；式（5）和式（6）保证只有在同一热轧计划内才考虑板坯热轧长度的限制；式（7）表示热轧计划的能力约束；式（8）表示板坯热轧同宽的限制；式（9）消除子回环；式（10）定义了热轧计划数的计算公式；式（11）～式（14）保证宽度下跳和宽度、厚度、硬度、出炉温度平滑变化。

2 热轧计划的单亲遗传算法

热轧计划编制问题是NP 难问题，而GA 可以有效地解决这类问题。传统的GA 在解决组合优化问题时会遇到一些问题，由于传统GA 编码影响交叉算子，文献［12］中提出在采用序号编码时，必须采用缺乏理论支持的部分匹配交叉（Partially Matched Crossover，PMX））、顺序交 叉（Order Crossover，OX）、循环交叉（Cycle Crossover，CX）等特殊的交叉算子；另外，传统遗传算法需要保持种群多样性且容易发生早熟收敛现象，文献［13-15］都对传统GA 的早熟收敛现象进行了研究。

目前，单亲GA 已成功运用到组合优化问题的求解过程中。文献［16］采用单亲GA 解决配电网络问题；文献［17］采用单亲GA 解决了作业车间调度问题；文献［18］采用单亲GA 解决了炉次计划编制问题。针对传统GA 的上述不足，本文采用一种改进算法即单亲GA，它取消了传统GA 的交叉算子，全部遗传操作都只在一个个体上进行。

2.1 算法参数确定

为提高单亲GA 的求解效率，本文对算法的交换方式、种群规模、进化代数进行优选。

（1）基因换位方式的确定

基因换位方式是将一条染色体上的基因相互交换，可以分为单点换位和多点换位。假设在规模为40、进化500代时，对单点交换、两点交换和三点交换的仿真实验结果（每种交换方式实验三次）进行对比，对比情况如图1所示。可以看出：单点换位能够快速收敛，而两点换位和三点换位在500代的收敛值仍然不够稳定。因此选择的搜索方式为单点换位。

（2）种群规模的确定

选择单点换位的方式，且暂定进化代数为500代，种群规模选择为10，20，30，40，50和60。设批量计划中的板坯数为［200，400］，对每个种群规模进行仿真实验，得到图2。由图2 可知：进化代数为500代、种群规模为40时，能够较快收敛且收敛值最低的，因此选择种群规模为40。

（3）进化代数的确定

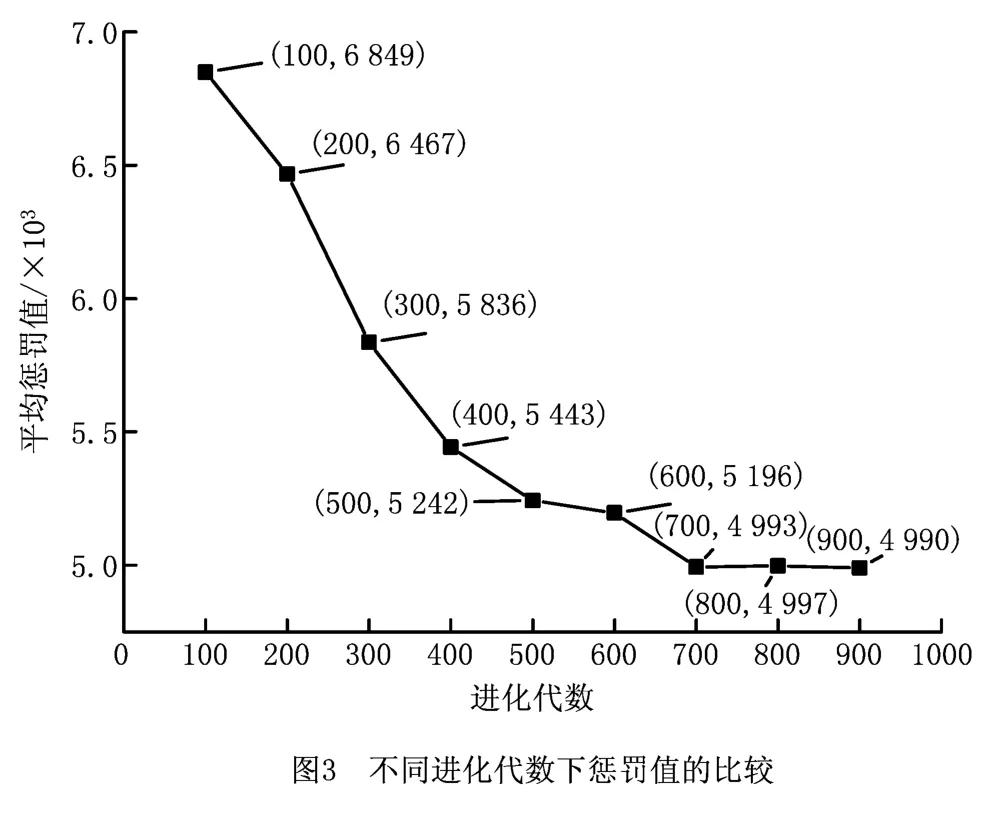
算法采用单点交换方式，种群规模为40，进化代数选择100，200，300，400，500，600，700，800 和900代，每一代实验三次，取三次结果的平均值，得到图3。从图3可知：随着进化代数的增加，平均收敛值在不断减少，直到700代以后，平均收敛值基本不变；在考虑单亲GA 结果的准确度和计算效率的情况下，确定进化代数为700代。

2.2 惩罚值确定

根据某钢厂的实际生产情况，并参考文献［1］，设定轧制宽度、硬度、厚度和出炉温度的跳跃惩罚值如表2～表5所示；根据从生产数据中提取出需要在交货期之前提前排产的订单的原则，取交货期的惩罚值pdij=0。轧制计划内的板坯轧制总长度和同宽板坯连续轧制长度根据编入轧制计划中的钢种特点而有所不同，例如C 钢系，设定一个热轧计划内的板坯总长度为100km，同宽板坯连续轧制的长度限制为40km。

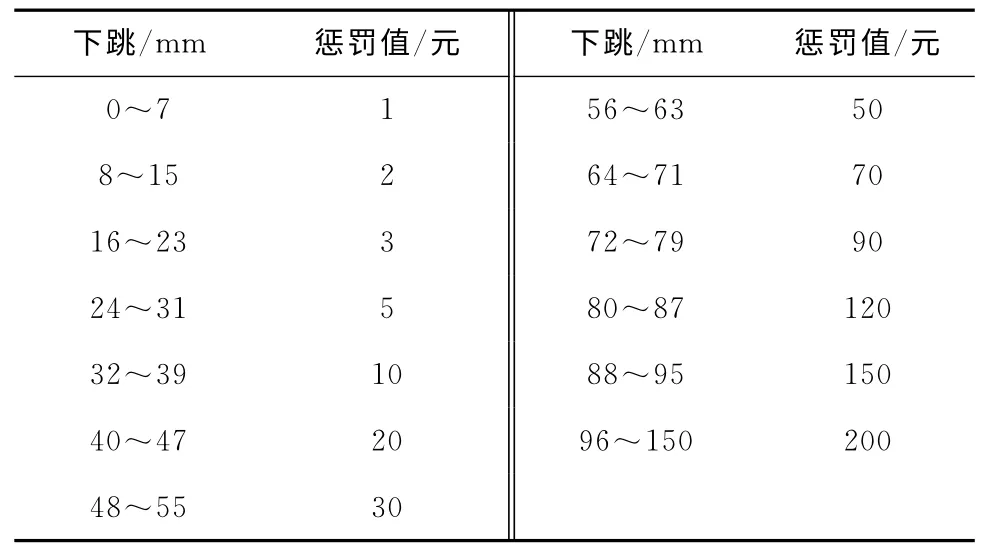
表2 宽度跳跃惩罚值

表3 硬度跳跃惩罚值

表4 厚度跳跃惩罚值

表5 出炉温度跳跃惩罚值

2.3 结合模型特征的求解策略

根据热轧规程构建热轧计划的数学模型，并运用单亲遗传算法求解。求解时，若能将模型特征知识嵌入单亲遗传算法中，则可以有效提高算法的求解性能。因此，下面结合模型特征给出如下求解策略：

（1）对于热轧计划数m的处理

热轧计划数m最小为热轧计划编制的优化目标之一。为保证最小化热轧计划数，算法作如下处理：

1）在算法初始阶段，首先提取单亲GA 的参数和待编制热轧计划的板坯数，应用式（10）对热轧计划数进行预估计，此时计算出热轧计划数的最小值，设热轧计划数m=mmin。

2）在迭代优化过程中，根据式（3）和式（4）可以避免某个板坯在某个热轧计划内或整个板坯序列不被重复计算，然后根据待编制热轧计划的板坯重新生成板坯序列，应用式（7）对热轧计划的能力进行累积，当超过给定的能力时，创建一个新的热轧计划。

3）当最后求出的惩罚值不满意时，令热轧计划数m=m+1，然后根据策略2）重新处理；若满意则结束计算。

（2）对于不可行解的处理

在算法求解过程中，每次迭代生成的热轧计划解可能存在不可行的情况。针对这一问题，本文通过设计惩罚值和适应度函数进行处理：

1）对于惩罚值的处理。在式（5）和式（6）条件的限制下，式（8）、式（11）～式（14）中热轧同宽的板坯超过最大长度，宽度、厚度、硬度、出炉温度变化不平滑，将惩罚值设定为一个极大正数（本文设定为50 000 元）。

2）对于适应度函数的设计。选择目标函数式（2）的倒数作为适应度函数，计算适应度函数的适应度值。若生成的解不可行，则根据惩罚值的处理方法，显然相应的适应度值为极小的值，远低于满足约束条件下的适应度值。根据轮盘赌选择方式，此时的适应度值不会被选择到，即可以避免计算结果跳出约束条件。

2.4 算法的求解步骤

在求解热轧计划编制问题时，采用单亲遗传算法，设计的步骤如下：

步骤1 编码。由于热轧计划编制问题是通过对板坯进行合理的排序来安排轧机生产，本文采用序号编码（通常所说的自然数编码），即以板坯号作为编码号。

步骤2 确定适应度函数。选择目标函数（1）和（2）的倒数为适应度函数，即f1=1／F，f2=1／G。

步骤3 根据初始种群个数，随机生成初始种群。

步骤4 分别计算种群各个体的适应度值，若达到终止条件，则得到最优解；若没有达到终止条件，则转步骤5。

步骤5 选择。采用较常用和有效的轮盘赌选择方式，即个体被选择的概率与所对应的适应度值成正比。首先选择f1最大的个体，当两个体的f1相同时，比较f2的大小，将较大者作为选择对象。每次选择十个最优结果保留到新种群。

步骤6 复制。按适应度大小进行复制，使下一代个体总数不变，即与初始种群规模相同。

步骤7 单点换位。对个体进行单点换位，产生新的个体，组成下一代种群，转步骤4。

3 仿真实验

采用Microsoft Visual C＃语言进行仿真，实验环境为Intel（R）Core（TM）2Duo CPU／2.80GHz／2.00GB／Windows7。求解过程中，采用某钢厂通过优化的订单数据与库存数据为初始数据，考虑小批量多品种和大批量少品种两类数据，对模型求解结果的正确性进行验证。

（1）优化的初始数据不存在B、D 和E钢种板坯

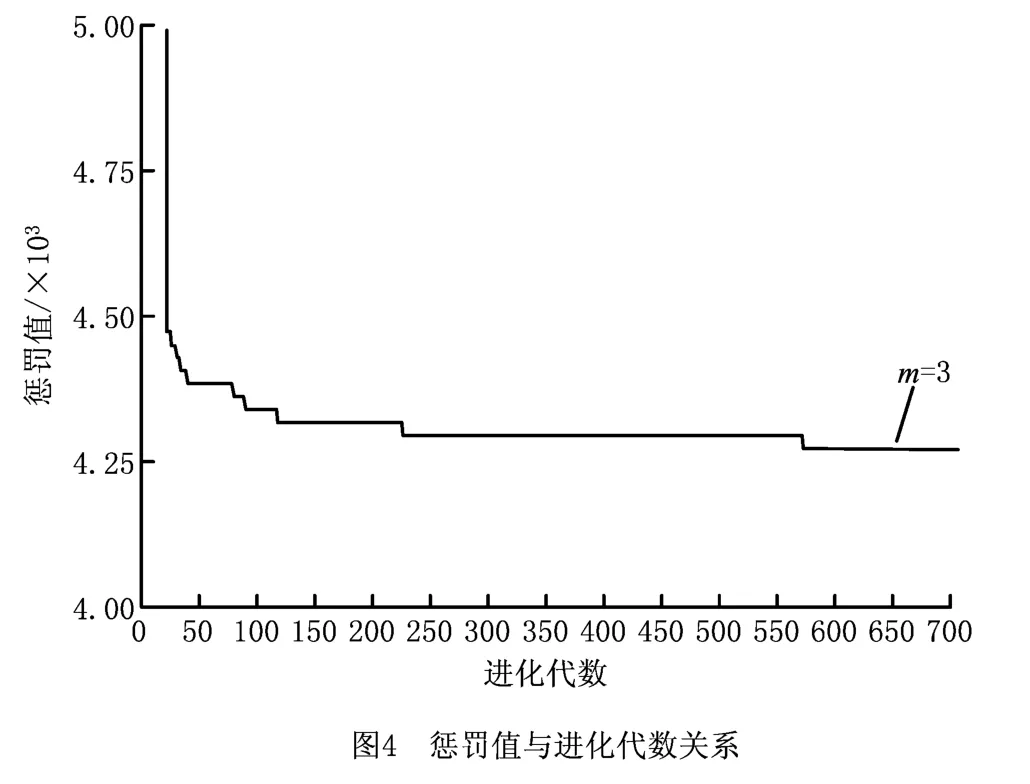
首先考虑小批量多品种的情况：选择200块板坯，其中有7 种钢种；然后考虑多批量少品种的情况：选择327块板坯，其中3种钢种。经过仿真实验得出的结果如表6所示。同时，给出大批量少品种情况下惩罚值与进化代数关系图，如图4所示，最后惩罚值都可以收敛到最低值，且最低值低于50 000元，说明单亲GA 和模型求解结果的正确性。

表6 仿真实验结果

从表6可以得出以下结论：

1）通过仿真实验，在小批量多品种或大批量少品种的情况下，目标函数的最低惩罚值分别为3 150元和4 270 元，都低于不合理解时目标函数惩罚值设定的50 000 元，说明了结果的有效性，从而验证了本文的模型和算法能够解决具有多品种小批量生产特征的热轧计划编制问题。

2）关于算法的计算效率，对于板坯数量在［200，400］规模的问题可以在10 min内获得问题的解，比人工编排热轧计划的效率提高了89%，而实际中一般的板坯数量规模是［100，300］，通常低于实验规模，因此本研究完全能够满足实际应用要求。

（2）优化的初始数据为B、D 和E钢种板坯

对B、D 和E钢种板坯分别进行仿真实验，得到的结果如表4～表7所示。从表4～表7可知：B、D和E钢种进行仿真实验后，可以分别得到相应最低且收敛的惩罚值802、980 和1 430，这些值都小于50 000，因此求解的热轧计划结果满足热轧规则。

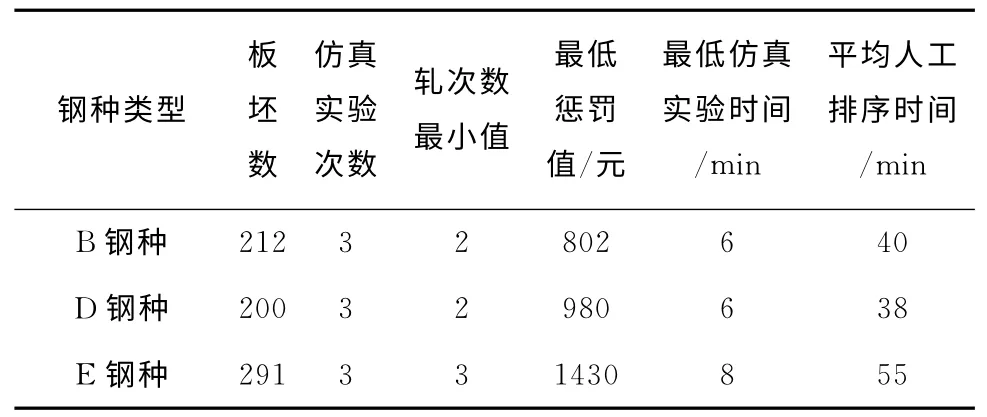
表7 仿真实验结果

从表7可以得出以下结论：

（1）在生产B、D 和E 钢种的情况下，目标函数的最低惩罚值分别为802 元、980 元和1 430 元，都低于不合理解时目标函数惩罚值设定的50 000元，说明问题模型以及针对该模型设计的算法能够有效解决不兼容钢种情况下的热轧计划问题；

（2）关于算法的计算效率，对于板坯数量在［200，300］规模的问题可以在8min内获得问题的解，比人工编排热轧计划的效率提高了85%，而实际中一般的板坯数量规模是［100，300］，因此本研究结果完全能够满足实际应用要求。

4 结束语

本文根据钢厂的实际生产要求，研究了考虑不兼容钢种和出炉温度跳跃因素的热轧计划编制问题。首先，针对存在不兼容钢种的情况，通过对板坯品种、规格和轧制工艺的分析，得出不兼容钢种热轧计划编制规程，避免编制在一个热轧计划内的板坯钢种冲突。在此热轧规程的基础上，进一步考虑了温度跳跃惩罚值，建立了热轧计划模型，将其归结为车辆路径问题（VRP），并设计了单亲遗传算法进行求解：通过对算法基本参数的实验分析，发现进化代数为700代，种群规模为40且单点交换方式有利于提高算法效率；结合模型特征给出求解策略，通过热轧计划的能力累积优化热轧计划数最小目标，惩罚值设定极大正数和目标函数的倒数为适应度函数来处理不可行解情况，由此来提高算法的求解性能。基于实际订单和库存数据的仿真实验表明，一方面，算法得到的最终惩罚值是收敛的，且小于50 000元；另一方面，模型和算法对于小批量多品种和大批量少品种两类情况均是适用的。

本文研究成果可为钢厂热轧计划编制尤其是订单和库存数据中存在多种钢种相互排斥情况下编制热轧计划提供一定的参考价值。今后将不断扩大热轧计划编制模型的适用范围，提高模型求解效率，构造更多、更复杂的应用情景来验证模型的准确性，进而在钢厂热轧计划实际编制过程进行大规模推广与应用。

［1］KOSIBA E D，WRIGHT J R，COBBS A E.Discrete event sequencing as a traveling problem［J］.Computers in Industry，1992，19（3）：317-327.

［2］JIA S J，ZHU J，YANG G K，et al.A decomposition-based hierarchical optimization algorithm for hot rolling batch scheduling problem［J］.International Journal of Advanced Manufacturing Technology，2012，61（5／6／7／8）：487-501.

［3］JIA S J，YI J，YANG G K，et al.A multi-objective optimisation algorithm for the hot rolling batch scheduling problem［J］.International Journal of Production Research，2013，51（3）：667-681.

［4］TU N，LUO X，HUANG H，et al.Method for hot rolling planning considering material requirements of downstream production lines［C］／／Proceedings of the 8th World Congress on Intelligent Control and Automation.Washington，D.C，USA：IEEE，2010：1690-1695.

［5］ZHANG Xujun，LYU Zhimin.Model and solution of integrated batch planning and scheduling for steelmaking-continuous casting-hot rolling［J］.Control and Decision，2013，28（8）：1257-1262（in Chinese）.［张旭君，吕志民.炼铸轧集成计划与调度组批模型 及算法［J］.控制与决策，2013，28（8）：1257-1262.］

［6］ZHANG Wenxue，LI Tieke.Batch plan optimization of steel integrated production with multiple processes［J］.Computer Integrated Manufacturing Systems，2013，19（6）：1296-1303（in Chinese）.［张文学，李铁克.面向多种生产工艺的冶铸轧一体化批量计划优化［J］.计算机集成制造系统，2013，19（6）：1296-1303.］

［7］ZOU Zonghua，LI Tieke.The model and algorithm for the CSP rolling planning［J］.Metallurgical Industry Automation，2003，27（2）：18-22（in Chinese）.［邹宗华，李铁克.CSP生产线轧制计划模型及算法［J］.冶金自动化，2003，27（2）：18-22.］

［8］YAO Xiaochun，HUANG Jianfeng.Cross-scheduling techniques for hot rolling planning of 1 880 mm hot mill of Baosteel［J］.Steel Rolling，2011，28（4）：71-72（in Chinese）.［姚筱春，黄剑峰.宝钢1 880mm 热轧机组轧制计划交叉编排技术［J］.轧钢，2011，28（4）：71-72.］

［9］HUANG Kewei，GU Yuming，DU Bin.Research and application of stainless steel hot rolling scheduling optimal system［C］／／Proceedings of the 7th China Steel Meating.Beijing：China Society for Metals（Ⅱ）.Beijing：The Chinese Society for Metals，2009：460-465（in Chinese）.［黄可为，顾玉明，杜 斌.不锈钢热轧生产排程模型优化系统［C］／／第七届（2009）中国钢铁年会论文集（下）.北京：中国金属学会，2009：460-465.］

［10］TANG Lixin，YANG Zihou，SHEN Hongyu，et al.Analysis of modeling factor of integrated lot planning for SM-CC-HRM［J］.Iron and Steel，2000，35（5）：74-76（in Chinese）.［唐立新，杨自厚，沈宏宇，等.炼钢-连铸-热轧集成批量计划因素分析［J］.钢铁，2000，35（5）：74-76.］

［11］ZHENG Zhong，LIU Yi，CHEN Kai，et al.Unifled modeli-ng and intelligent algorithm of production planning for the process of steeling-continuouscasting-hot rolling［J］.Journal of University of Science and Technology Beijing，2013，35（5）：687-693（in Chinese）.［郑 忠，刘 怡，陈 开，等.炼钢—连铸—热轧生产计划编制的统一模型及智能算法［J］.北京科技大学学报，2013，35（5）：687-693.］

［12］LARRANAGA P，KUIJPERS C M H，MURGA R H，et al.Learning Bayesian network structures by searching for the best ordering with genetic algorithms［J］.IEEE Transactions on Systems，Man &Cybernetics，Part A（Systems &Humans），1996，26（4）：487-493.

［13］REN Qingsheng，ZENG Jin，QI Feihu，et al.Self-crossover operator［J］.Control Theory and Applications，2001，18（4）：525-528（in Chinese）.［任庆生，曾 进，戚飞虎，等.自交叉算子［J］.控制理论与应用，2001，18（4）：525-528.］

［14］YE Yongfang，DU Yongqing，XING Xiaoshuai.An improved genetic algorithm of suppressing premature convergence［J］.Journal of Shanxi Normal University：Natural Science Edition，2010，24（2）：24-28（in Chinese）.［曳永芳，杜永清，行小帅.一种抑制早熟收敛的改进遗传算法［J］.山西师范大学学报：自然科学版，2010，24（2）：24-28.］

［15］POTTS J C，GIDDENS T D，YADAV S B.The development and evaluation of an improved genetic algorithm based on migration and artificial selection［J］.IEEE Transactions on Systems，Man and Cybernetics，1994，24（1）：73-86.

［16］ZHANG Wenjun，CHENG Haozhong，WANG Yi，et al.Distribution network optimal planning based on tree structure encoding partheno-genetic algorithm［J］.Transactions of China Electrotechnical Society，2009，24（5）：154-160（in Chinese）.［章文俊，程浩忠，王 一，等.基于树形结构编码单亲遗传算法的配电网优化规划［J］.电工技术学报，2009，24（5）：154-160.］

［17］LIU Shenghui，ZHANG Shuli，WANG Bo，et al.Partheno genetic algorithm for solving job-shop scheduling problem［J］.Computer Engineering，2009，35（5）：188-190（in Chinese）.［刘胜辉，张淑丽，王 波，等.一种求解单件车间调度问题的单亲遗传算法［J］.计算机工程，2009，35（5）：188-190.］

［18］WANG C，LIU Q，LI Q Y，et al.Optimal charge plan model for steelmaking based on modified partheno-genetic algorithm［J］.Control Theory &Applications，2013，30（6）：734-741.