作业车间类型多机器人制造单元调度算法

杨煜俊，龙传泽，陶 宇

（广东工业大学 广东省计算机集成制造重点实验室，广东 广州 510006）

1 问题的提出

随着计算机集成制造技术的快速发展，传统的制造业发生了重大而深刻的变革。社会的发展使人工成本越来越昂贵，为了应对市场环境的变化，企业开始大量采用工业机器人与自动化技术提高生产效率、降低人工成本。搬运机器人是工业机器人的一种，它能灵活快速地实现物体的转运，因而被广泛应用于制造业。机器人制造单元是由搬运机器人、机床、搬运导轨等硬件和控制软件组成的新型智能制造系统（如图1），它能显著提高生产效率。近年来智能柔性制造单元也成为学术研究和工业应用的热点，特别是单元调度问题。目前，国内外大多相关研究集中在制造单元流水车间类型调度问题［1-2］，文献［3］研究了带搬运约束的流水车间作业调度问题，文献［4］使用一种新的编码方法设计了两种解决经典作业车间调度问题的粒子群算法，该方法在求解传统作业车间调度问题上有较好的效果，但没有考虑搬运时间。文献［5］构造了一个新的领域结构，使用改进禁忌搜索算法解决带单台搬运机器人的作业车间调度问题，但没有扩展考虑带多台搬运机器人情况下搬运任务的分配，在较大规模的制造单元内往往有多台搬运设备，而任务的分配策略将影响制造单元的生产效率。文献［6］探讨了使用混合整数线性规划方法来解决含自动导向小车（Automated Guided Vehicle，AGV）的柔性制造系统（Flexible Manufacturing System，FMS）调度问题，这种整数规划方法只能解决较小规模的作业车间调度问题。文献［7-8］研究了考虑单元布局影响的三台机床组成的柔性制造单元纯周期时间优化调度问题，该方法局限于由三台机床与一台搬运设备组成的制造单元。文献［9］用遗传算法解决了带单台搬运机器人、有限缓存区的作业车间制造单元调度问题，但传统的遗传算法收敛速度慢、局部搜索能力差，难以在有限时间内找到全局最优解。文献［10］提出一种并行策略来提高优化效率，按照顺序和倒序规则构建两个初始解，使用并行禁忌搜索算法求解单台机器人制造单元调度问题，但禁忌搜索算法对初始解的要求较高，单一的局部搜索算法很难跳出局部最优解。西北工业大学车阿大教授课题组主要针对流水车间调度问题，对机器人制造单元调度模型与算法进行了深入研究［11-12］。

总体来看，国内外学者大多的研究集中在经典的流水车间和作业车间问题上，这类研究大部分建立在不考虑搬运时间的假设基础上，只有少数研究考虑了搬运时间，但也只考虑了单台搬运设备的情况。为此，本文将重点研究考虑搬运时间的作业车间多机器人制造单元调度问题。

2 问题描述

作业车间多机器人制造单元的调度问题可描述为：n个加工工件J=｛J1，…，Jn｝在m台机床M=｛M1，…，Mm｝上加工。有r台搬运机器人R=｛R1，…，Rr｝为加工工件在机床间提供搬运。满足以下约束条件：

（1）每个加工工件Ji有ni道加工工序，用Oi1，Oi2，…，Oin表示，每道加工工序的加工时间已知且只能在指定的机床上加工，每个工件在每台机床上只加工一次。

（2）每台机床同一时间只能加工一个工件，每台机器人同一时间只能搬运一个工件。

（3）如果工序Oij与工序Oij+1不在同一台机床上加工，则当工序Oij加工完成时，在执行下一道工序Oij+1之前，必须由指定的一台机器人完成搬运工序，机器人搬运时间与机床间距离成正比。

（5）开始调度时，每个工件都处于其第一道加工工序机床的输入缓存区。

另外，假设机床的输入输出缓存区的负载能力是无限的。即：

（1）机床的输入缓存区有足够多的位置存放机器人搬运过来的待加工工件。

（2）机床的输出缓存区有足够多的位置存放加工完成后待搬运的工件。

（3）工件在输入缓存区、加工工位、输出缓存区之间的切换自动完成，且不考虑其切换时间。

本问题目标是求解一个可行的调度方案，使最大完工时间最小，目标函数可表示为Cmax=min｝，其数学模型表示如下：

其中：

式（1）为目标函数，Cik为工件Ji的最后一道工序在机床Mk的完工时间；

式（2）表示在同一台机床上加工的工件的时间约束，Pjk为工件Jj在机床Mk上加工的一道工序的加工时间，Cjk为工件Jj在机床Mk上的完工时间，A为一个足够大的整数；

式（3）表示同一个工件不同工序的加工时间约束，Cik为工件Ji在机床Mk上的加工完成时间；

3 析取图模型

作业车间多机器人制造单元调度问题析取图模型可以用公式G=（VM∪Vr，E∪DM∪DR）表示。其中：VM为加工工序节点集合（包括0和＊两个虚节点）；VR为机器人搬运工序TRrij的集合；E为工件的加工工序约束；DM为机床的析取弧集合，DR为搬运机器人的析取弧集合。机床与机器人的所有析取弧都确定方向后组成完全选集S=SM∪SR，其中：SM为机床选集，SR为机器人选集。完全选集S可通过三个向量MS，TS和RA表示。

机床选集SM用向量MS表示，一个工件Jj有nj道加工工序，因此MS包含nj次工件号j。MS中第一次出现的工件号j代表工件Jj的第一道加工工序Oj1，下一次出现的工件号代表工件Jj的第二道加工工序Oj2，以此类推。加工工序在向量MS中的位置代表该工序的加工顺序。MS可以充分确定机床上工件的加工顺序，因此MS可以充分代表机床选集SM。

机器人搬运选集SR由加工工件号重复排列组成的向量TS确定。工件加工完后搬运至卸载站的时间不考虑，加工工件Jj有nj-1道搬运工序TRrij，因此TS包含nj-1个数字j。

RA是由分配给搬运工序的机器人编号重复组成的向量。向量RA的每个位与向量TS一一对应。TS（i）=j，RA（i）=P表示向量在位置i的工件Jj的搬运工序分配给机器人P。

例如：四个加工工件、每个工件四道工序（四台机床）、三台搬运机器人组成的4×4×3调度问题。由上述模型描述可知，本问题有十六道加工工序和十二个搬运工序（不计搬运机器人空载工序）。加工时间和加工机床安排如表1所示。

表1 4×4×3调度问题描述

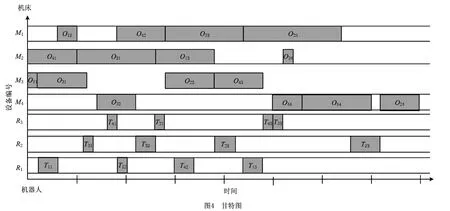
图2 给出了一个可行调度方案的三向量MS，TS和RA表示。机床上工件的加工顺序由向量MS定义，根据向量MS的编码和表1的描述可知各机床上工序的加工顺序为：①机床1：O12→O42→O33→O23，②机床2：O41→O21→O13→O34，③机床3：O11→O31→O22→O43，④机床4：O32→O44→O14→O24；结合向量TS和RA可知机器人的搬运顺序为：①机器人1：T11→T12→T42→T13，②机器人2：T31→T32→T22→T23，③机器人3：T41→T21→T43→T33。该调度问题对应的析取图和甘特图如图3和图4所示。

图3中标注出了一条从起点0到终点＊、耗时最长且机床加工工序间和机器人搬运工序间无时间间隔的路径，称为关键路径。在这条关键路径上的加工工序和搬运工序称为关键工序。所有工件中最后一道工序的完工时间就是该调度问题的最大完工时间Cmax，因此关键路径的长度可以完全决定最大完工时间Cmax，关键路径上关键工序的微调可以改变最大完工时间Cmax。本文基于关键路径上的机床块和机器人块的微调来构造邻域结构：

（1）在关键路径上，无时间间隔相邻的两道以上机床的加工工序组成一个机床块。

（2）在关键路径上，无时间间隔（空载时间不算时间间隔）相邻的两道以上机器人的搬运工序组成一个机器人块。

（3）在关键路径上，前后没有相邻加工工序的独立的一道加工工序作为独立机床工序。

（4）在关键路径上，前后没有相邻搬运工序的独立的一道搬运工序作为独立机床工序。

（1）选集S关键路径Ps上某些机床块内的某些加工工序的相对位置发生转变。

（2）选集S关键路径Ps上某些机器人块内的两道搬运工序的相对位置发生转变。

（3）选集S关键路径Ps上独立机器人工序分配的机器人发生变化。

4 算法设计

在上述析取图构建的邻域搜索结构的基础上，结合遗传算法的全局搜索能力，设计本调度问题的算法。

4.1 遗传算法简介

遗传算法是由美国Holland教授首次提出的，之后由其他学者进行了完善和改进。遗传算法是根据自然界的优胜劣汰、适者生存的遗传机制演化而来的随机搜索算法，其主要特点是能根据群体中的个体对环境的适应度自动指导搜索方向。良好的全局搜索能力使遗传算法被广泛应用于组合优化、机器学习、车间作业调度等领域。应用遗传算法时首先对种群进行初始化；然后对种群个体的适用度进行评价；最后经过选择、交叉和变异操作，得到下一代群体。

4.2 算法设计

根据上述模型的表述，本调度问题需要同时考虑工件的加工顺序、机器人的搬运顺序和搬运工序的分配，比一般的作业车间调度问题复杂很多。针对这类涉及多层调度的问题，采取分层调度的方式可以将问题分步简化，本文采用三层调度方案：

第一层：机床加工工序调度，即不考虑搬运工序的情况下，通过调度算法求得一组使完工时间最小的加工方案。

第二层：机器人搬运工序调度，即根据机床加工顺序，安排机器人在机床间的搬运顺序。

第三层：使用启发式规则将每道搬运工序分配给各台机器人，使总完工时间最小。

4.2.1 个体编码

本问题的编码方式有很多种，其中最直接的是工序编号编码，这种编码方式在进化过程中容易产生不可行解，因此每一次进化都需对个体编码进行可行性判断。为保证每个编码在遗传算子操作中的可行性，本文采用重复的序列编码方式，在第一层调度中用基于工序约束的个体编码方式，编码中的每个基因代表工件号，同一个工件的所有工序用同一个工件号表示，相同的工件号出现的先后次序代表该工件的加工工序号。假设一个4×4（四个不同的工件在四台不同的机床上加工）的第一层编码MS可表示为：4 3 4 2 3 1 2 4 2 3 1 2 1 3 4 1，所代表的加工先后次序为：工件4的第一道工序、工件3的第一道工序、工件4的第二道工序，以此类推。

机器人的搬运工序顺序是根据先完成先搬运的启发式规则确定的，即在确定了加工顺序的基础上插入机器人搬运工序，再根据相邻搬运工序分配给不同机器人的启发式规则为各台机器人分配搬运工序。例如：在确定机床工序MS：1 3 2 3 2 1 2 1 3后，根据先完成先搬运的规则可确定机器人搬运顺序为TS：3 1 2 3 1 2，再根据相邻搬运工序分配给不同机器人的启发式规则，如果机器人的数量为2可得RA：1 2 1 2 1 2，对应的搬运顺序为：机器人1搬运工件3，机器人2搬运工件1，机器人1搬运工件2，机器人2搬运工件3，机器人1搬运工件1，机器人2搬运工件2。同理如果机器人数量为3，则RA：1 2 3 1 2 3。

4.2.2 算子设计

遗传算子的设计将影响算法的性能和收敛，重要的遗传算子有选择、交叉和变异三种。

（1）适应函数

适用度函数一般与目标函数直接相关，可以通过目标函数评估适用度，适用度大的个体有较大的生存机会。作业车间类型机器人制造单元的调度问题以最小化最大完工时间为目标函数，完工时间越小，该个体的适用度越好。因此通过目标函数Cmin的尺度转换确定适用度函数为：。

（2）选择操作

遗传算法根据个体对环境的适用度，通过优胜劣汰法则选择子代，本算法根据轮盘赌法选择子代，适用度大的个体进化到下一代的概率大，适用度小的个体进化到下一代的概率相对较小。这种选择方式既保证了下一代中基因的质量，又保证了基因的多样性。对规模为N的种群，如果其中个体i的适应度值为fi，则个体i能进化到下一代的概率。

（3）交叉操作

交叉是指两个父代染色体的部分基因片断交叉互换、生成新的子代的操作，是种群内部个体之间的信息交流。本文使用一种新的基于工序编码操作的交叉方式，它产生的子代能够很好地继承父代的优良基因，使目标值更接近最优值。该交叉操作的示意图如图5所示，图中＊为去除指定的标号片段，首先选择父代1染色体中的一个编号（如图5中的编号3），将该编号及其位置保持不变并进化到子代1中；然后在另一个父代2中标记出该编号，将去除该编号的父代2中的其他编号依次填入子代1中，得到完整的子代1。同理得到子代2。

（4）变异操作

通过一定概率的变异运算可以防止算法陷入局部极值，找到全局最优值，常用的变异方式有插入变异、交换变异和反序变异。反序变异算子在搜索空间中搜索到的领域聚集度较高，因此在遗传算中使用反序变异，具体操作如图6所示。

4.2.3 局部搜索

局部搜索算法搜索邻域通过关键路径Ps构建，根据关键路径上的搬运工序或加工工序是否连续，将关键路径上的工序分为四种片段类型：机床块Bm、机器人块Br、独立机器人工序Ir、独立机床工序Im。针对不同的类型片段采用不同的操作方法来构建邻域：

（1）机床块Bm内移动 移动机床块Bm内加工工序的相对位置，机床块内非第一道加工工序移动到所有加工工序之前加工（改变向量MS）。

（2）机器人块Br内互换 机器人块Br位置的i（1≤i≤｜Br｜-1）的搬运工序分别与其后面某位置的j（i≤j≤｜Br｜）搬运工序互换位置（改变向量TS）。

（3）独立机器人工序重分配 将该道搬运工序分配给另一台机器人（改变向量RA）。

（4）独立机床工序不变 工序位置保持不变。

这种领域搜索方式将遗传算法的个体编码作为局部搜索的初始解，通过调整关键路径上的工序来更新向量MS、TS和RA，大大缩小了搜索空间，提高了效率。局部搜索算法流程图如图7所示。

4.3 算法流程

将遗传算法与局部搜索算法相结合，得到作业车间多机器人制造单元调度问题的混合遗传算法流程，如图8所示。

5 算例分析

引入OR-Library 上40 个不同规模的FT、LA、ABZ、ORB 系列基 准算例 和文献［17］中 的Philippe算例，加入机器人搬运工序，假设机器人在机床间的空载移动时间为1，机器人对每道工序的搬运时间按TRij=D（i-j）计算，其中：i-j为机床间的距离，D为距离系数，R为搬运机器人数量。遗传算法的参数选定为：种群规模60、最大迭代次1 000、代沟0.8、交叉率0.7、变异率0.09。在MATLAB R2010 软件下运行，系统运行环境为Window 7 2.5GHz／4G RAM PC。分别使用本文提出的混合遗传算法与传统遗传算法在不同的参数下对各个算例进行仿真，每个算例分别运行10次，对实验结果进行统计，结果如表2所示。

混合遗传算法与传统遗传算法的平均收敛代数与平均收敛时间对比如图9和图10所示，当D=3、R=2时两种算法求得的最优值对比如图11所示。由此可知，将邻域搜索算法与遗传算法相结合组成混合算法，虽然增加了单代的运算时间，但混合算法的收敛速度明显快于传统遗传算法，因此混合算法不管是从运算时间还是从运算结果上看，都优于传统遗传算法。

表2 FT、LA、ABZ、ORB系列算例实验结果

续表2

在表2中，不考虑搬运时间即D=0时，混合遗传算法对82.9%的算例都求得了已知的最优解，其余17.1%也求得了近似最优解。考虑搬运时间即D≠0 的可参考算例很少，将本算法的实验结果与文献［17］中Philippe提出的算例结果进行对比，结果如表3所示，通过对比可知，本算法优于Philippe提出的算法。

在表3中，当距离系数D相同时，随着搬运机器人的数量从1增加到3，最大完工时间逐渐减小，当D=3时，最大完工时间平均减小13.0%。由此可知，通过增加搬运机器人的方式，可以提高作业车间机器人制造单元的生产效率，且搬运时间越长，效果越明显。

表3 Philippe算例对比

单独对作业车间知名算例FT06 进行深入分析，距离系数D分别取1，3，5，机器人数量R从1递增到5，实验结果如表4 所示。当D=1 和D=2时，搬运机器人数量达到3后，即使再增加搬运机器人求得的最优值也不变；当D=3，搬运机器人数量达到4后，即使再增加机器人求得的最优值也不变。这种情况表明机器人数量处于“饱和状态”，再增加机器人只会增加成本，而无法提高生产效率。

表4 FT06算例

续表4

6 结束语

本文建立了作业车间多机器人制造单元的数学优化模型和析取图模型，用带局部邻域搜索策略和启发式任务分配规则的混合遗传算法对问题进行求解。通过OR-Library上40个不同规模的FT、LA、ABZ、ORB系列基准算例及Philippe算例对混合遗传算法进行了验证，实验结果证实了混合遗传算法从运算时间和运算结果上都优于传统遗传算法和Philippe算法。通过实验数据分析得出结论：当搬运时间相对于加工时间很小时，搬运工序对最大完工时间几乎无影响；当搬运时间较大时，将显著增加完工时间，增加搬运机器人数量可以提高作业车间机器人制造单元的生产效率，且搬运时间越长，效果越明显。未来工作中将对考虑机器柔性、工序柔性的机器人制造单元调度问题进行研究。

［1］DAWANDE M W，GEISMAR H N，SETHI S P，et al.Sequencing and scheduling in robotic cells：recent developments［J］.Journal of Scheduling，2005，8（5）：387-426.

［2］DAWANDE M W，GEISMAR H N，SETHI S P，et al.Throughput optimization in robotic cells［M］.Berlin，Germany：Springer-Verlag，2007：1-413.

［3］HURINK J，KNUST S.A fast tabu search algorithm for the job shop problem［J］.Management Science，1996，42（6）：797-813.

［4］HURINK J，KNUST S.Makespan minimization for flop-shop problems with transport time［J］.Discrete Applied Mathematics，2001，112（3）：199-216.

［5］HURINK J，KNUST S.Tabu search algorithms for Job-Shop problems with a single transport robot［J］.European Journal of Operational Research，2005，162（1）：99-111.

［6］CAUMOND A，LACOMME P，MOUKRIM A，TCHERNEV N.An MILP for scheduling problem in an FMS with one vehicle［J］.European Journal of Operational Research，2009，199（3）：706-722.

［7］GULTEKIN H，KARASAN O E，AKYURK M S.Pure cycles in flexible robotic cells［J］.Computers &Operations Re-search，2009，36（2）：329-343.

［8］GULTEKIN H，AKTURK M S，KARASAN O E.Scheduling in a three-machine robotic flexible manufacturing cell［J］.Computers &Operations Research，2007，34（8）：2463-2477.

［9］LACOMME P，TCHERNEV N.Resolution of a job-shop problem with a single transport robot and buffer facilities［C］／／Proceedings of 2006International Conference on Service Systems and Service Management.Washington，D.C.，USA：IEEE，2006，2：1108-1113.

［10］HE Zhizhou，YANG Yujun，CHEN Xindu.Parallel tabu search scheduling algorithm for job-shop with transport robot［J］.Industrial Engineering Journal，2013，16（4）：122-125（in Chinese）.［何之洲，杨煜俊，陈新度.带搬运机器人的Job-Shop问题的并行禁忌搜索算法［J］.工业工程，2013，16（4）：122-125.］

［11］YAN Pengyu，CHE Ada，LI Peng，YANG Naiding.Scheduling model and its algorithm for no-wait robotic cell with mul-tiple robots［J］.Computer Intergrated Manufacturing Systems，2010，16（2）：404-410（in Chinese）.［晏鹏宇，车阿大，李鹏，杨乃定.具有柔性加工时间的机器人制造单元调度问题改进遗传算法［J］.计算机集成制造系统，2010，16（2）：404-410.］

［12］CHE Ada，WANG Yuan.Scheduling model and its algorithm for no-wait robotic cell with multiple robots［J］.Computer Intergrated Manufacturing Systems，2008，14（3）：525-534（in Chinese）.［车阿大，王 远.无等待多机器人制造单元调度模型和算法研究［J］.计算机集成制造系统，2008，14（3）：525-534.］

［13］LACOMME P，LARABI M.A disjunctive graph for the jobshop with several robots［EB／OL］.［2014-10-26］.http：／／www.mistaconference.org／2007／papers／A%20Disjunctive%20Graph% 20for% 20the% 20Job% 20Shop% 20with%20Several%20Robots.pdf.