制约济南岩溶大泉持续喷涌的主因素阈值研究

周 娟，邢立亭，2，滕朝霞，王立艳

（1．济南大学 资源与环境学院，济南 250022；2．山东省地下水数值模拟及污染控制工程技术中心，济南 250022；3．济南市水利局，济南 250099）

0 引 言

受岩溶发育程度、降雨、人类活动等诸多因素影响，岩溶地下水水位动态复杂多变，但存在一定规律性，如年内季节变化、年际周期性变化与长期趋势及随机波动［1，2］．我国岩溶分布广泛［3］，南北方的岩溶发育程度、岩溶水动态特征都存在一系列差异，南方岩溶较北方发育充分，其岩溶水对降雨的响应也较为灵敏［4］．岩溶水位变化能够直接反应岩溶含水层的储水量变化［4］，且易被监测．降雨与地下水位的相关性研究表明，北方岩溶水位具有明显的季节性变化［5］．

由于人类活动的影响，地下水位与降雨的相关趋势发生了变化．例如，大量开采地下水会引起水位大幅度下降，人工回灌又会引起地下水位上升．降雨与地下水位的相关研究主要是基于统计学原理的随机模型法，例如多元回归法、时间序列法、频谱分析等，还有采用人工神经网络、黑箱模型法、灰色分析和核函数法等［6－12］．小波分析被应用于地下水位的模拟与预测，效果较好［13，14］．

济南岩溶水含水层多为奥陶系灰岩，裂隙岩溶发育，岩溶水位对自然因素和人为影响的响应十分敏感．自1959年以来，济南岩溶水系统地下水经历了少量开采（1959—1967年）—超量开采（1968—1980年）—限采、回灌（1981—今）等阶段［15］．基于泉水位约束，相关研究提出了保泉的允许开采量［16］，并指出人工回灌对济南泉水系统具有一定的修复作用［17－19］．但是以往研究缺乏对降雨和回灌的定量研究，造成人工回灌具有极大盲目性．为此，本文从地下水位动态要素入手，研究维持泉水位稳定的回灌量和降雨“阈值”，为济南岩溶水保护和管理提供依据．

1 水文地质概况

济南市地处鲁中山地的北缘，南依泰山，北临黄河，地形南高北低，南部为绵延起伏山区［20］．泉域的范围为南起南部山区，北至济南岩体和石炭、二叠纪地层，东为东坞断裂，西至马山断裂［20］．南部山区为自然分水岭，北边界主要是岩浆岩，东坞断裂为一条整体阻水局部弱透水的断裂，西部边界为马山断裂，其南段阻水，北段前隆一段为透水边界，断裂两侧水力联系密切（见图1）．

图1 济南岩溶水系统水文地质略图Fig．1 Hydrogeological sketch map in Karst water system of monoclinal structure in Jinan

泉域以太古界泰山群（Art）为基底，上覆古生界寒武系、奥陶系、石炭系及二叠系，新生界古近、新近系、第四系松散堆积物．泰山群出露于南部山区，寒武系、奥陶系自南向北展布，在南部山区裸露分布，是济南泉水的重要降雨补给区．第四系主要分布北部的山前倾斜平原，泉群以北第四系下伏岩浆岩，岩体阻水（见图1）．

泉域内的主要含水层为寒武系和奥陶系碳酸盐岩裂隙－岩溶含水层，地下裂隙岩溶发育良好，是济南岩溶水的重要储存空间亦是运移通道．由于裂隙发育不均，加之构造、地形、埋藏条件等因素，其富水性、径流强度等存在差异（见图1）．泉域在南部接受大气降雨补给，总体上自南向北运动，在北部受岩体阻挡，沿裂隙破碎带上升，形成济南四大泉群（见图2）．

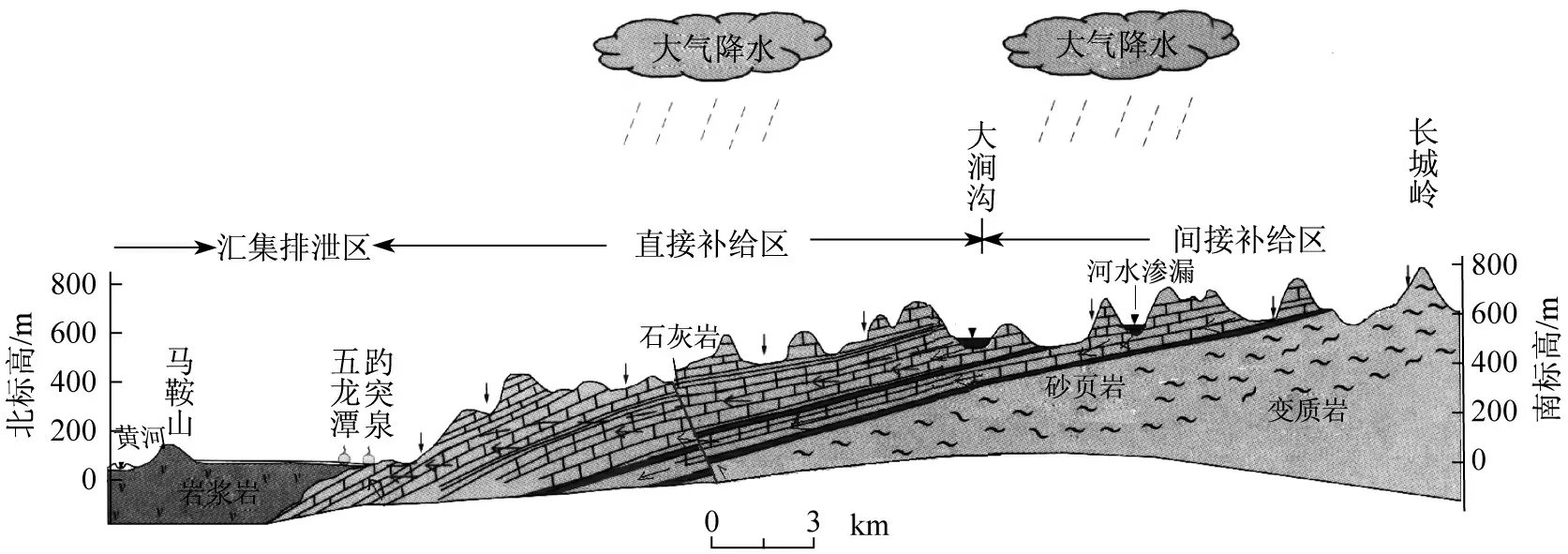
图2 泉水成因剖面示意图（引自《济南泉水》，略加修改）Fig．2 Sectional view of the spring forming reason

2 济南泉域降雨特征

基于济南市1916—2012年的降雨资料分析，年均降雨量为633．2 mm，年际最大降水量1 160．0mm，最小降水量为302．8 mm，相差857．2 mm，可见济南市的年际降雨分配不均（见图3），但降雨特征呈现一定周期性和随机性［7，8］．

选取2008—2012年降雨资料分析年内降雨变化情况，绘制各季度的降雨分布（见图4）．年内降雨主要集中在6—8月份，12月及次年1—2月份降雨最少，每一年各季度的分配比例有明显差异．2008年和2009年3—4月降雨比例较其他几年偏大，分别是23．02%和26．86%，这两年降雨主要集中在5—8月份；2010年6—8月份降雨占全年的78．64%，而3—4月份降雨比例仅为7．1%；2011年6—9月份降雨占全年降雨的82．07%；2012年降水量总体偏少，5月份降雨仅为7．4 mm，9月份降雨仅为36．1 mm．

图3 1916—2012年年降雨量Fig．3 Annual precipitation from1916 to 2012

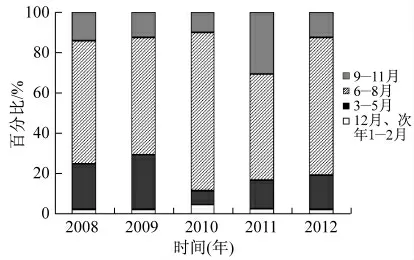
图4 2008—2012年各季度降雨比例Fig．4 The precipitation proportion of the four quarter

济南市降雨年际明显差异和年内内降雨分布不均，影响地下水位的动态变化．如果当年降雨期缩短，翌年降雨稀少，泉水将面临断流的危险．与此同时，济南城区向泉水补给区扩张，地面硬化，降雨入渗面积和地下水补给量减小［20］，近年来的水位动态表明，现状开采条件下仅仅依赖降雨补给来维持枯水期泉水位的稳定及泉水正常喷涌是不现实的，因此在枯水季节利用人工回灌补源是十分必要的．

3 泉水位动态类型

济南市泉水位动态变化呈上升迅速，下降略缓的趋势，具有典型的季节性特点，在6月份水位降为最低值，9月份水位出现峰值（见图5）．泉水位过程曲线代表着岩溶含水层水量的变化，载有补给、开采、岩溶发育程度等信息，因此分析泉水位过程曲线是十分有必要的．

图5 2008—2012年月降水量与泉水位的关系Fig．5 The relationship between precipitation and spring water level

以往研究表明，不同岩溶发育地区地下水位动态存在5种曲线特征类型［21］，其对应的岩溶发育程度见表1．地下水位动态线型特征系数αn可采用下式计算：

式中，tanαup为动态曲线上升支的平均坡度的正切；tanαdown为动态曲线下降支的平均坡度的正切．

计算得出济南泉水水位动态线型的不对称系数αn均在1．02～1．29之间，由表1可知，该区地下水动态曲线符合不对称尖峰型，表明济南泉域地下水属于补排中速型，丰水期、枯水期水位变幅大，裂隙岩溶发育程度偏高，人工干预可有效确保泉水正常喷涌．

表1 地下水位历时线型表Tab．1 Duration curve type table of underground water level

4 泉水位回升降雨阈值的确定

4．1 泉水位回归—自回归分析

（1）开采量与泉水位关系分析

影响济南泉水位变化的因素较为复杂，且影响因素是动态可变的．以1968—1989年济南市地下水开采量较大的时段建立地下水位与降水量、开采量的多元回归方程［8］：Y＝27．362＋0．002 X1－0．278 X2－0．05 X3＋0．001 X4，其中，X1、X2、X3、X4分别表示当年降水量、市区开采量、外围开采量、前一年降水量．回归分析表明，1968—1989年期间人工开采量是影响济南泉水位的主要因素．

为分析泉水位与开采量之间的相关性，绘制1959—1989年平均泉水位与泉域开采量的散点图表明（见图6），随着开采量的增加，泉水位呈现下降趋势（R2＝0．778），泉域最大开采量达到31．18万m3／d．济南市基于保泉目的，自2003年以来加大黄河水供水，减少地下水开采量，岩溶水开采量分为两段7．8～12．67万m3／d（枯水期）和16．22～20．08万m3／d（丰水期）（见图7），绘制该时期无回灌、无降雨时段的地下水开采量与泉水位的散点图（见图7），由图可见，地下水开采量与泉水位无明显的相关性，因此将地下水开采量较小且稳定的情况下，地下水开采量不再是影响泉水位变化的主要因素．文献［8］中也指出，1990年以后开采量有所减少，开采总量稳定，地下水位出现波动变化与开采量关系不显著．

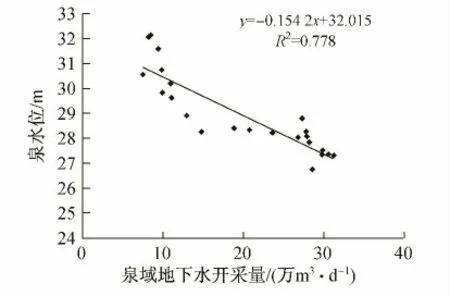
图6 1959—1989年平均泉水位与开采量关系曲线Fig．6 The relationship between groundwater exploitation and the annual average spring water level in 1959—1989

图7 2003—2012年地下水开采量与泉水位关系图Fig．7 The relationship between Groundwater exploitation and spring water level in 2003—2012

（2）泉水位自回归分析

从图5中可以看出，虽然实施回灌补源措施，但枯水期地下水位呈现下降趋势，在6月份达到最低水位．因此，在7．8～12．67万m3／d（枯水期）和16．22～20．08万m3／d（丰水期）开采量稳定条件下，枯水期维持泉水位稳定是保泉的关键，研究降水量和回灌量对地下水位变化的影响极为重要．

大气降雨对泉水位的影响具有滞后延迟的特点，因此地下水水位不仅受本时段降雨的影响，还受前一时段、前两个时段等的影响．又由于地下水径流、排泄作用，前一时段的水位对地下水位自身具有一定的影响．因此，本时段降雨、前一时段降雨以及前一时段地下水位都是影响泉水位变化的因变量，由此引入回归—自回归模型，其表达式为

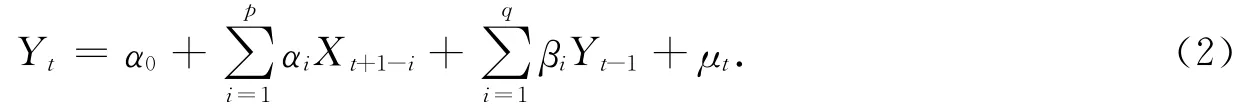
其中，Yt表示当月泉水位，Xt、Xt－1表示本月降雨量、前一月降雨量，Yt－1表示前一月地下水位，α0、αi、βi为回归参数，μt为随机变量，p、q＝1，2，…．

采用2008—2012年月泉水位与月降雨量数据，经SPSS软件分析得回归方程为

y＝0·008×10－5x3－0·004×10－2x2＋0·008x－0·186，

相关系数R＝0．79．在显著性为0．01的水平下进行F检验，p值为1．97×10－11＜0．01，回归方程有效，模型具有实际意义．

自变量Xt的回归系数α1对应的显著性Sig值为0．827＞0．01，则该变量对因变量Yt显著影响较小；自变量Xt－1的回归系数α2对应的显著水平Sig值为1．23×10－8＜0．01，Yt－1的回归系数β1对应的显著水平Sig值为8．409×10－6＜0．01，则自变量Xt－1和Yt－1对因变量Yt有显著影响．由此可见，当月降水量对地下水位变化的贡献不大，前一个月降水量与前一个月水位对当月地下水位具有显著影响．主要原因在于雨水到达地面，在下渗过程中，需首先满足上层土壤及岩层的需水量，过剩的水量继续下渗到达岩溶含水层，这一过程必然导致地下水位变化滞后于降雨．上述分析结果显示，滞后期最大为一个月，这一结论与济南泉水位在历年9月底出现年内最高水位的实际情况完全吻合．

4．2 降雨阈值的估算

图5表明，水位过程线与降雨有“滞后”关系，特别是降雨大于50 mm时，地下水位均有相应的上升，随后地下水位均开始下降．如2010年8月降雨达到387 mm，相应的地下水位陡升，而后下降．

泉水位变化滞后于降雨，但雨季和旱季存在差别．在雨季，水位波动变化对雨量反映十分敏感，在旱季，则比较迟钝．旱季降水量先满足植被截留、土壤需水，多余的水量才能补给地下水．如2009年11月—2010年5月，在这期间有超过20 mm的降水量，泉水位不升反降（见图8），此时20 mm的降雨不足以下渗补给地下水．可见，泉水位上升的降水量必须超过一个“阈值”．

图8 旱季降雨与泉水位关系Fig．8 The relationship between precipitation and spring water level in dry season

水位变幅是指某一时段末水位与该时间段初始水位变化差值．为消除固体潮朔望日对水位的影响，选用2008—2012年泉水位月变幅进行研究，以泉水位月变幅为y，月降水量x，绘制散点图（见图9a）．

拟合的趋势线方程用多项式表示为y＝α1＋α2x＋α3x2＋…，其中，y表示泉水位月变幅，x表示月降水量，α1、α2…为回归参数．

数据拟合结果显示，自变量x为一次时的趋势方程为y1＝0．003 8x－0．141 1，相关系数R＝0．83，说明散点的分布符合多项式形式．基于拟合性质，随着x次数升高，相关系数越大，当自变量x的最高次数为3次时，自变量x和因变量y的相关系数达到R＝0．85，趋势方程为

y2＝0·008×10－5x3－0·004×10－2x2＋0·008x－0·186·

线性拟合曲线和三次多项式曲线与横坐标的交点对应的月降水量分别为37．13 mm和26．65 mm，分析多年观测数据，例如，在2006年9月份，此阶段无地下水回灌，该月降水量为31．6 mm，地下水位上升为0．07 m．可见31．6 mm月降雨足以引起泉水位的抬升，由此可见，三次多项式在求取拐点时更具有合理性．

延长样本容量，选用2004—2012年的泉水位月变幅进行研究（见图9b）．数据拟合结果显示，自变量x为1次时的趋势方程为y1＝0．003 7x－0．152 4，相关系数R＝0．81．自变量x的最高次数同样为3次时，自变量x和因变量y的相关系数R＝0．824．趋势方程为

y2＝0·006×10－5x3－0·003×10－2x2＋0·007x－0·189·

线性拟合曲线和三次多项式曲线与横坐标的交点对应的月降水量分别为41．19 mm和30．73 mm．同样，线性拟合求的交点对应的降水量为41．19 mm不符合实际．

图9 2004—2012年水位月变幅与月降水量关系Fig．9 The monthly spring water level variation and precipitation

虽然泉水位月变幅与月降水量之间存在良好的线性、非线性关系，但线性拟合结果反演的降水量偏大与实际不符，3次拟合结果符合实际情况，认为三次多项式拟合曲线适合济南市月泉水位变幅与降水量的关系．可以概括y＝ax3－bx2＋cx－d，（a、b、c、d＞0）．虽然样本容量越大代表性越强，但误差也会较大，引起泉水位上升的降水量临界值增大，考虑土壤含水量差异以及地下水位埋深等因素，因此给出该地区引起月泉水位上升的月降水量“阈值”的一个范围为26．65～30．73 mm．

济南岩溶水系统的月降水量阈值与羊庄岩溶水系统存在差异，文献［22，23］中通过8个不同岩性的试验场百次降雨入渗试验给出裸露型岩溶区、半覆盖型岩溶区及第四系土层包气带最大截留量方程：Emax＝9＋22．6lg（D＋0．4）、Emax＝10＋33lg（D＋0．498）、Emax＝36＋40．3 lg（D＋0．128），其中，Emax为包气带最大截留量，D为水位埋深．其降水阈值存在差异的原因有含水介质、水位埋深［23］、地形地貌、地表岩溶发育程度等因素，济南泉域含水介质主要为奥陶系灰岩，羊庄盆地岩溶水系统主要为寒武纪灰岩，两者地质背景条件存在较大的差异；另一方面，羊庄盆地岩溶水系统是通过均衡试验场取得次降水入渗系数，本文以月为时间尺度研究枯水期降水与泉水位的关系，从而推求枯水期泉水位不下降的月累计降雨量，用以判断是否需要进行回灌．济南泉域岩溶水水位埋深大部分在30～150 m之间，华北平原第四系孔隙水水位埋深一般小于5m，因此本研究得出的济南泉域降水阈值大于华北平原地区，亦符合本区的实际水文地质条件．

5 回灌对泉水位影响

以2004、2006和2008年枯水期的回灌、降雨及泉水位资料为研究对象，2006年回灌期间处于泉水位下降期，自4月27日起开始回灌，共22 d，回灌量33万m3／d（见图10）．

回灌前地下水位均匀下降，回灌开始之后，地下水位开始上升．回灌前共117 d，最大一次降雨3．4 mm，属于无效降雨，可以忽略其对泉水位的影响，此期间水位共下降0．96 m，由此推算出自然状态下泉水位日均降幅为8．2×10－3m．回灌期间地下水位上升值共为0．42 m，加上泉水位的自然降幅0．18 m，则回灌和降雨引起的地下水回升值共为0．60 m．为剔除5月4日58 mm降雨的干扰，选取4月27日—5月3日来推算回灌引起的泉水位上升值，在这7 d有两次3 mm的降雨可以忽略，泉水位共上升0．105 m，则日均升幅15×10－3m．同理，推算回灌引起泉水位上升的日均幅为23．2×10－3m，推算22 d回灌引起的地下水位回升值为0．51 m，由此得出一次58 mm的降雨引起的地下水位回升值约为0．09 m．

2008年回灌时间3月14日—5月20日，回灌共68 d（见图11），回灌量21．5万m3／d．同理推测，自然日均降幅为9．7×10－3m，回灌引起地下水位回升日均幅为11．89×10－3m．

2004年回灌的时间是从1月1日开始，一直持续到4月28日（见图12），历时118 d，回灌水量为16万m3／d．

图10 2006年回灌与泉水位关系Fig．10 The relationship between groundwater recharge and spring water level in 2006

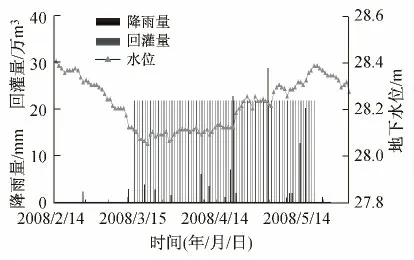
图11 2008年回灌与泉水位关系Fig．11 The relationship between groundwater recharge and spring water level in 2008

2004年回灌期间泉水位处于下降趋势，较2006年、2008年同时期泉水位的下降幅度要缓．泉水位变化具有阶段性差异：①1月1日—2月13日泉水位稳定阶段，16万m3／d的回灌量所引起的泉水位回升幅度与泉水位自然降幅相抵消；②2月13日—3月11日泉水位迅速下降阶段，该阶段泉水位下降主要是由农灌抽取地下水所致，泉水位平均下降16．3×10－3m／d；③3月11日—3月19日水位短暂稳定阶段；④3月19日—4月28日泉水位波动下降阶段，主要由灌溉需水所致．可见，枯水期16万m3／d的回灌量可维持泉水位的相对稳定或者减缓泉水位下降幅度．

绘制2004、2006和2008年的回灌量与回灌引起的泉水位回升值散点图（见图13），可以发现回灌水量与回灌引起的泉水位回升值呈显著线性关系，相关系数R＝0．996，回灌对泉水位具有显著性影响．当回灌量超过16．56万m3／d时，回灌所引起的泉水位回升幅度大于泉水位自然下降幅度，可确保泉水持续喷涌不断流．

图12 2004年回灌与泉水位关系Fig．12 The relationship between groundwater recharge and spring water level in 2004

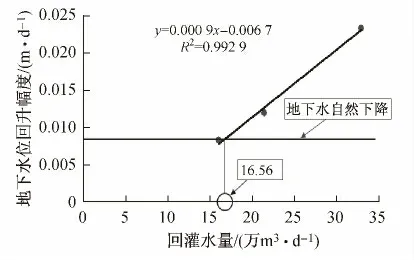
图13 回灌水量与泉水位回升幅度关系Fig．13 The amount of spring water level increase and recharge

6 结 论

（1）从地下水位动态曲线类型表明济南的岩溶裂隙发育较好，济南岩溶泉水位对气候及人类影响反应较为敏感，前一个月降水量对地下水位具有显著影响．

（2）枯水期维持济南泉水动态稳定的月降雨“阈值”为26．65～30．73 mm，否则需要实施人工回灌补源．

（3）回灌水量与回灌引起地下水位回升幅度呈显著线性关系（R＝0．996），基于保泉的回灌水量需大于16．56万m3／d．岩溶水开采量应考虑降水季节变化、年际变化分时开采，枯水期地下水开采量不宜超过7．8万m3／d，丰水期不超过16．2万m3／d．

［1］王维泰，梁永平，王占辉，等．中国北方气候变化特征及其对岩溶水的影响［J］．水文地质工程地质，2012，39（6）：6－10．

［2］FAN Y H，HUO X L，HAO Y H，et al．An assembled extreme value statistical model of karst spring discharge［J］．Journal of Hydrology，2013，504（11）：57－68．

［3］袁道先．中国岩溶学［M］．北京：地质出版社，1993：1－8．

［4］ELLEN K H，LAURA T，WILLIAM B W．Quantifying the place of karst aquifers in the groundwater to surface water continuum：A time series analysis study of storm behavior in Pennsylvania water resources［J］．Journal of Hydrology，2009，376：307－317．

［5］王大纯．水文地质学基础［M］．北京：地质出版社，1995：100－101．

［6］陈葆仁，洪再吉，汪福炘，等．地下水动态及其预测［M］．北京：科学出版社，1988．

［7］张建芝．济南泉域地下水动态特征及监测网优化［D］．济南：济南大学，2011．

［8］张建芝，邢立亭．回归分析法在地下水动态分析中的应用［J］．地下水，2010，32（4）：88－90．

［9］JAN C D，CHEN T H，HUANG H M．Analysis of rainfall－induced quick groundwater－level response by using a Kernel function［J］．Paddy Water Environment，2013（11）：135－144．

［10］胡克祯，张建芝，邢立亭．基于时间序列分析的地下水动态研究［J］．水科学与工程技术，2011（5）：32－34．

［11］MAO X M，SHANG S H，LIU X．Groundwater level predictions using artificial neural networks［J］．Tsinghua Science and Technology，2002，7（6）：574－579．

［12］吴东杰，王金生，滕彦国．小波分解与变换法预测地下水位动态［J］．水利学报，2004，（5）：49－44．

［13］DAMIR J，VESNA D J．A frequency domain approach to groundwater recharge estimation in karst［J］．Journal of Hydrology，2004，289：95－110．

［14］祁晓凡，杨丽芝，韩晔．济南泉域地下水位动态及其对降雨响应的交叉小波分析［J］．地球科学进展，2012，27（9）：970－978．

［15］王茂枚，束龙仓，季叶飞，等．济南岩溶泉水流量衰减原因分析及动态模拟［J］．中国岩溶，2008，27（1）：19－23．

［16］邢立亭．济南泉域岩溶水环境保护［J］．水利科技与经济，2006，12（9）：601－604．

［17］吴兴波，牛景涛，牛景霞，等．人工回灌对济南泉水系统修复的影响［J］．人民黄河，2004，26（8）：20－22．

［18］牛景涛，吴兴波，宋星原，等．济南回灌补源与抽水试验研究［J］．人民长江，2004，35（11）：47－48．

［19］章亦兵．济南市人工回灌补源保护泉水的研究［D］．南京：河海大学，2005．

［20］徐军祥，邢立亭，魏鲁峰，等．济南岩溶水系统研究［M］．北京：冶金工业出版社，2012：26－35．

［21］邹成杰．岩溶地区地下水位动态分析［J］．中国岩溶，1995，14（3）：261－269．

［22］李传谟，康凤新．山东羊庄岩溶水系统水资源及增源增采最佳开发研究［G］／／山东省地质矿产局主编．山东地质矿产研究文集．济南：山东科学技术出版社，1996：224－227．

［23］李传谟，康凤新．岩溶水资源及增采模型［M］．济南：山东科学技术出版社，1999：51－56．