基于QPSO算法的OSPF多约束路由研究

江家宝 郑尚志

（巢湖学院 计算机与信息工程学院，安徽 巢湖 238000）

0 引 言

随着网络通信要求的不断提高和Internet的飞速发展，路由器成了网络连接中最为关键的设备．路由器中运行的软件对网络连接的性能和效率的影响越来越明显．目前国内外OSPF网络路由器的主流产品仍然使用SPF算法解决路由问题，为了缓解网络路由的瓶颈和拥塞问题，在考虑到各种路由协议的前提下，人们陆续提出了遗传算法、模拟退火算法等多种方法实现OSPF协议．

本文的目的是研究QPSO算法在多约束OSPF网络路由选择中的应用［1］，研究内容包括：

●使用QPSO算法进行OSPF网络路由选择；

●比较QPSO、遗传和SPF算法进行OSPF网络路由选择的有效性．

以下首先介绍OSPF路由工作原理以及Qos（Quality of service）路由问题；其次，简述量子粒子群算法（QPSO：Quantum－Behaved Particle Swarm Optimization）［2－3］的基本概念和实现方法；然后，详细阐述考虑网络路由选择过程中必需满足的Qos和实时性等多种要求，在目标函数值的引导下，如何实现QPSO和遗传算法［3］对复杂的OSPF网络路由解空间进行有效搜索，获得最佳路由和多条次路由，并有效地利用这些路由进行路由规划；最后，用仿真实验进行验证，比较SPF、QPSO和遗传算法的实验结果并给出相关结论．

1 OSPF协议原理

路由就是在网络数据传输中采用某种策略为数据包从源点到达目的地点寻找一条理想路径［3］．基于全局最优思想，网络设备为转发的数据包选择某种距离测度下的最优路径，沿最优路径发送数据包．支持OSPF协议的SPF算法在尽力传送业务服务模式的网络中工作得较好，但它无法满足多媒体业务的Qos需求，主要表现如下：

（1）SPF采用与链路带宽成反比的cost值度量距离来寻找最优路径，没有考虑其它约束条件，不能满足日益复杂的网络性能要求．

（2）SPF忽略了次路由，一旦最优路径发生拥塞，其它可用路径被闲置，从而大大降低网络传输性能．

拥塞时，网络的时延和丢包率会剧增，如果采用时延和丢包率来度量最优路径，可以将流量转移到另一条路径上去，但这种转移是全部转移，新路径又会由于负荷过重而拥塞，而原来的路径又会空闲，这样会引起路由振荡．因此，我们需要选取新的OSPF实现方法，使其能满足日益复杂的Qos要求．

2 Qos路由问题

CCITT给出Qos［4－5］的定义：“Qos是一个综合指标，用于衡量使用一个服务的满意度”．而现有的Internet都只是提供Best－effort传送，不能提供Qos保证．为了适应网络的需求发展，Internet工作组提出的新草案对Qos要求如下：①提供可计量的服务；②支持高级应用（如双向交互音／视频，远程设备控制等）；③良好的可扩展性；④可管理性；⑤能与终端用户操作系统和中间件协同工作等．要求Qos选路既要可行（即可达），又要有效（即最小化占用链路带宽，最小化链路拥塞等）．因此，为了满足Qos路由要求，路由规划时首先考虑如何有效利用网络资源，其次考虑如何减少路由计算的时间复杂性．

本文首次采用经过QPSO算法修正的OSPF路由来解决上述问题．

3 Qos路由模型

网络链路的双向特征一般不同，网络的拓扑结构可用有向图G＝（v，e）来描述（V为网络节点集合，E为节点间链路集合）．链路（v，e）的特性可用链路的可用剩余带宽band（v，e）、时延delay（v，e）（包含数据包在节点的处理时延、排队时延和发送时延）、丢包率loss（v，e）、发送报文所需的代价cost（v，e）（是链路费用和传播时延的综合评价）来表示．

当网络中源节点S与目的节点D通信时，记：P（S，D）为源节点S到目的节点D的一条具有k段链路的可达路径，（vi，ei）为路径P（S，D）的第i段链路，即（vi，ei）∈P（S，D），i＝1，2，…，k，则路径P（S，D）的特征参数设置为：①总代价cost（S，D）＝∑cost（vi，ei）），②可用剩余带宽band（S，D）＝min｛band（vi，ei），i＝1，2，…，k｝，③总丢包率loss（S，D）＝1－∏（1－loss（vi，ei）），④总时延delay（S，D）＝∑delay（vi，ei）．这样，基于带宽、时延、丢包率和代价等多种约束的Qos路由问题可表述为：在满足约束band（S，D）≥Bmin，delay（S，D）≤Dmax和loss（S，D）≤Lmax条件下，使得链路总代价cost（S，D）→min，其中Dmax、Bmin和Lmax分别为业务要求的时延上限、带宽下限和丢包率上限．要全面衡量一条路由的优劣，必须对上述Qos路由标准进行综合评价，为此设计如下目标函数：

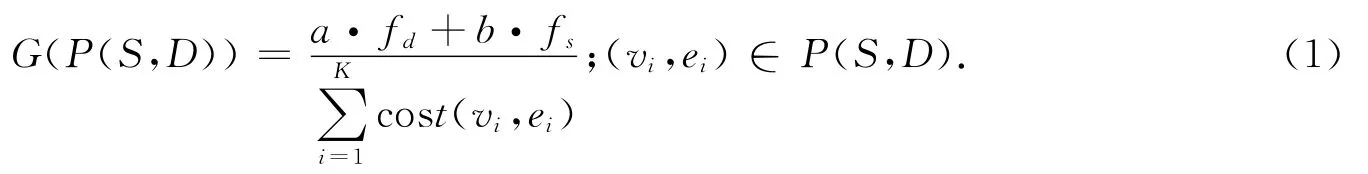
式中，加权系数a，b分别表示时延和带宽在目标函数中所占的比例（a＝1－b）．fd＝∏Fd（delay（vi，ei）－Dmax），当delay（vi，ei）＞＝Dmax时链路时延罚函数Fd（delay（vi，ei）－Dmax）的值为小于1的正数λ，否则为1．fs＝∏Fs（S（vi，ei）＋Lmax－1），其中S（vi，ei）是一个随带宽增大而减小的函数，当S（vi，ei）＋Lmax＜1时链路带宽罚函数Fs（S（vi，ei）＋Lmax－1）值为1，否则为小于1的正数μ，本文S（vi，ei）＋Lmax－1取（1－Lmax）＊（30／band（vi，ei）－1）．

4 QPSO算法简介

QPSO算法是在粒子群算法基础上开发的一种新的优化算法，不但参数个数少，而且搜索能力高于所有已开发的粒子群算法．记：目标函数为f（X）、群体中微粒数为S、微粒j当前位置为Xj＝（Xj1，Xj2，…，Xjn）、微粒j所经历的当前具有最佳目标函数值的位置（即局部最优点）为Yj＝（Yj1，Yj2，…，Yjn）、群体所经历的当前具有最佳目标函数值的位置（即全局最优点）为Gb＝（Gb1，Gb2，…，Gbn）；Yj由式（2）确定，Gb由式（3）和（4）确定：

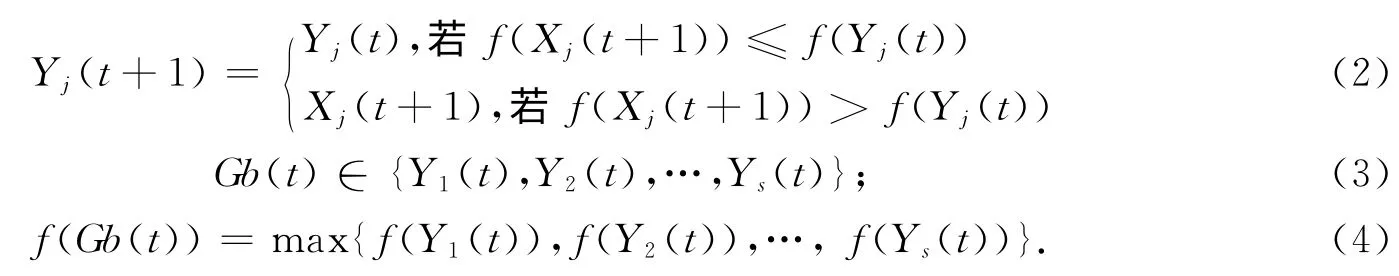
算法进化如下：

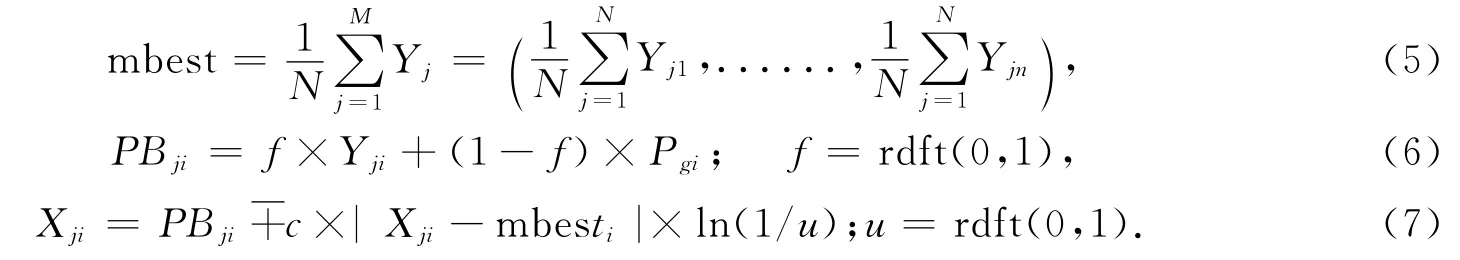
下标ji表示粒子j的第i维．t表示第t次进化；函数rdft（0，1）产生（0，1）之间的随机小数；mbest是微粒群局部最优点Y的中间位置；PBj为粒子j的局部最优点Yj和全局最优点Gb之间的随机点；公式（7）以0．5的概率取“＋”或“－”操作；c为收缩扩张系数，是QPSO收敛的重要参数，根据具体情况可以固定为某一值，也可以随迭代线性地从一个值递减到另一个值．

5 OSPF路由选择的实现

我们采用十进制编码方案．以路径中节点的十进制标号序列作为路径编码值．比如，路径编码表示的路径为

5．1 QPSO算法的实现

设网络节点数为N，QPSO算法的初始化分以下三步：第一，随机初始化PopSize个粒子的最初位置，粒子j代表路由起点和终点的p［j］．path［0］和p［j］．path［N－1］由输入得到，固定不变；利用自定义函数rdint（0，N）产生［0，N］之间随机整数初始化p［j］．path［1：N－2］，并要求路径可达且无重复节点；计算路径的各特征参数；根据公式（1）计算粒子j的目标函数值p［j］．fit；利用p［j］．fit降序链表记录现已找到的可达路由．第二，初始化粒子j的局部最优点为：p［j］．pb＿path［0：N－1］＝p［j］．path［0：N－1］；p［j］．pb＿band＝p［j］．band；p［j］．pb＿cost＝p［j］．cost；p［j］．pb＿delay＝p［j］．delay；p［j］．pb＿loss＝p［j］．loss；p［j］．pb＿fit＝p［j］．fit；p［j］．pb＿Qosfit＝p［j］．Qosfit．第三，初始化全局最优点为：Gb．path［0：N－1］＝p［0］．path［0：N－1］；Gb．band＝p［0］．band；Gb．cost＝p［0］．cost；Gb．delay＝p［0］．delay；Gb．loss＝p［0］．loss；Gb．fit＝p［0］．fit；Gb．Qosfit＝p［0］．Qosfit．

算法每次迭代对所有粒子都依次进行“进化、评估、取代”操作．

（1）进化．这是算法的核心，对粒子j路径数组P［j］．path［i］（0＜i＜N－1）进行如下操作：步骤A，利用公式（5）和公式（6）计算mbest［i］、Pb［j］．path［i］．步骤B，利用公式（7）计算粒子第i维新坐标x，结果是浮点数，按0．5的概率向上或向下取整后对（N＋1）取余．步骤C，是进化的难点所在，假设路径数组P［j］．path［i］≠0，P［j］．path［i＋1，＋2，…．，k－1］均为0，则定义P［j］．path［i］为P［j］．path［k］的前驱节点．若x值非法（是负数、起点、终点、已经经历过的节点），则从［0，N］中随机选取一个合法值给x．若x＝0或与P［j］．path［i］前驱节点可达，p［j］．path［i］＝x；否则作如下修正，记p［j］．path［i］前驱节点p［j］．path［m］的直达节点集合为A，p［j］．path［0：m－1］经历过的节点集合为B，从集合A－B中随机选取一点赋给p［j］．path［i］．若集合A－B为空，则p［j］．path［m］以0．5的概率赋值0，以0．5的概率作上述修正，处理完p［j］．path［m］后再重新处理p［j］．path［i］．以此类推，极端情况是向前递推处理到p［j］．path［1］，这时肯定能从起始位置的直达节点中找一个节点作为p［j］．path［1］的值，否则起始节点就是孤立点（无解）．步骤D，若p［j］．path［i］为终点，则p［j］．path［i，i＋1，．．，N－2］＝0，进化结束．若i＝N－2，则检查p［j］．path［N－1］能否直达前驱节点，若直达则进化结束，否则用类似步骤C的方法处理其前驱节点．

（2）评估：计算粒子各路径特征参数和目标函数值p［j］．fit，如果是新路由，则插入按目标函数值降序排列的可达路由链表．

（3）取代：比较目标函数值，若p［j］．pb＿fit＜p［j］．fit；则用个体当前位置信息取代当前最佳位置信息；若Gb．fit＜p［j］．fit，则用个体当前位置信息取代全局最佳位置信息．

5．2 遗传算法的实现

遗传算法［6］与QPSO的初始化相同．利用轮盘赌方法实现选择算子．以概率Pc进行交叉操作，交叉方法是：①找出用于交叉的父代个体A和B路径上的所有相同节点；②从相同节点中随机选取两个用于交叉产生两个新个体；③若新个体中有相同节点，则删除相同节点间的链路（参见图1）．以概率Pm进行变异操作，变异方法是：先对路径节点p［j］．path［i］以概率p更新，再仿照QPSO进化操作步骤C的方法进行相应的处理．

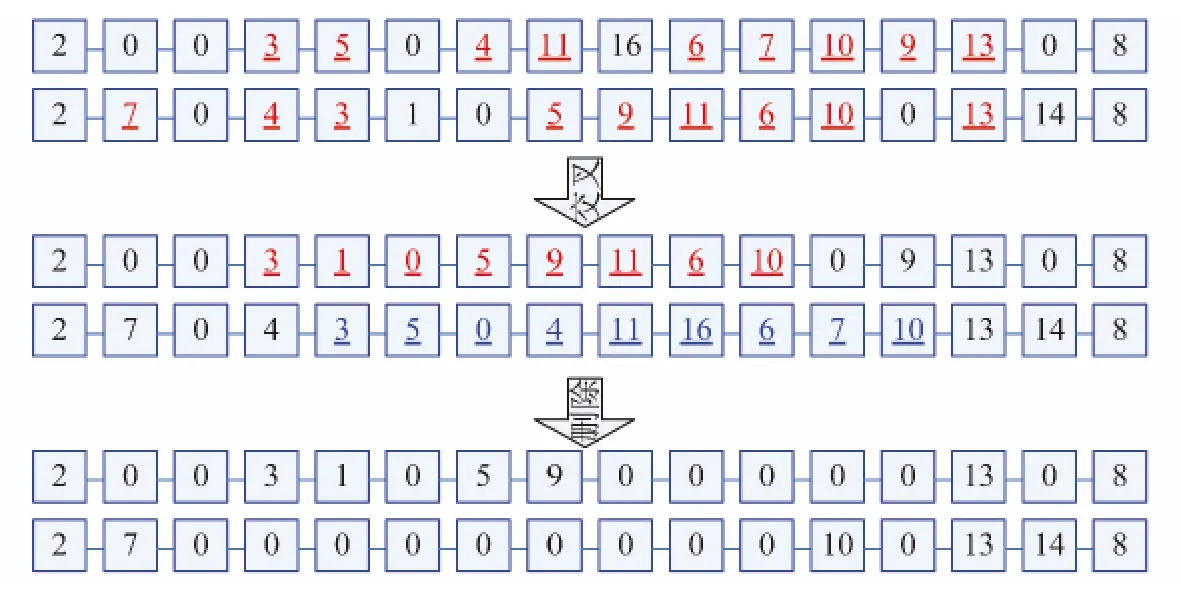
图1 交叉操作示例图Fig．1 The example of crossover operation

6 实证结果

6．1 OSPF网络构建

为了更具有一般性，实验时构建如图2所示的节点数N＝28的网络，图中每条连线都代表双向链路，且链路特征一般不同．除了少数特殊节点（如节点27）外，绝大多数节点的入度和出度均大于1，这样，绝大多数节点间就有多条路由．网络状态初始化方法如下：G．node＿delay［i］＝rdft（0．001＊D＿max，0．2＊D＿max）；G．trans＿delay［j］［i］＝rdft（Dmax＊0．001，Dmax＊0．02）；G．band［j］［i］＝rdft（0．5＊Bmin，Bmax）；G．cost［j］［i］＝rdft（0．001＊Cmin，0．1＊Cmax）；G．loss［j］［i］＝rdft（L＿max＊0．001，L＿max＊0．3）；G．edge＿delay［j］［i］＝G．node＿delay［i］＋G．trans＿delay［j］［i］；函数rdft（x，y）的功能是产生（x，y）之间的随机浮点数．

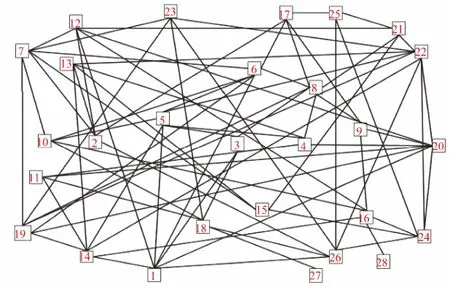
图2 实验网络拓扑图Fig．2 The example of network topology

目标函数常量a和b的设置主要看实际的网络注重时延和带宽的程度，若侧重于追求时延小，则设置a＞b；当某段链路的时延大于Dmax时，罚函数Fd＝λ的值设置越小，目标函数值也就会越小，一般设置λ≤0．3；当某段链路的带宽小于一定的值时，罚函数Fs＝μ的值设置越小，目标函数值也就会越小，一般设置μ＝0．5左右．本文侧重于追求网络时延小，故此目标函数常量设置为：a＝0．6，b＝0．4，λ＝0．1，μ＝0．5．链路特征值的上下限设置取决于实际网络的性能要求；本文设置为：带宽下限Bmin＝0．1 Mbps，带宽上限Bmax＝10 Mbps，花费下限Cmin＝1，花费上限Cmax＝200，时延上限Dmax＝250ms，丢包率上限Lmax＝0．001．

为了对比分析，QPSO算法和遗传算法的网络拓扑结构、网络状态数据初始化、群体大小（20）、主循环次数（500）都对应相同．遗传算法的交叉概率Pc＝0．4，变异概率Pm＝0．06．QPSO的收缩扩张系数c按照迭代循环次数线性地从4．0递减到0．1．

6．2 实验结果

为了对比分析，选取多对节点进行测试：表1列举了具有代表性的6个节点的仿真结果，表2列举了具有代表性的3对节点的测试结果．

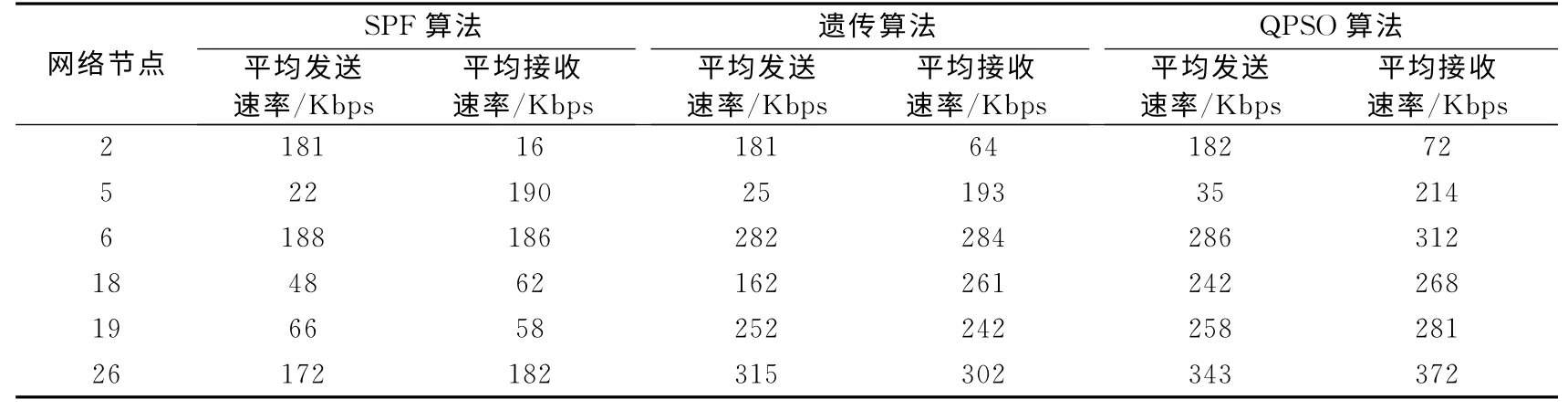
表1 SPF、QPSO与遗传算法的几组仿真结果Tab．1 Some simulation results of the SPF algorithm，genetic algorithm and QPSO

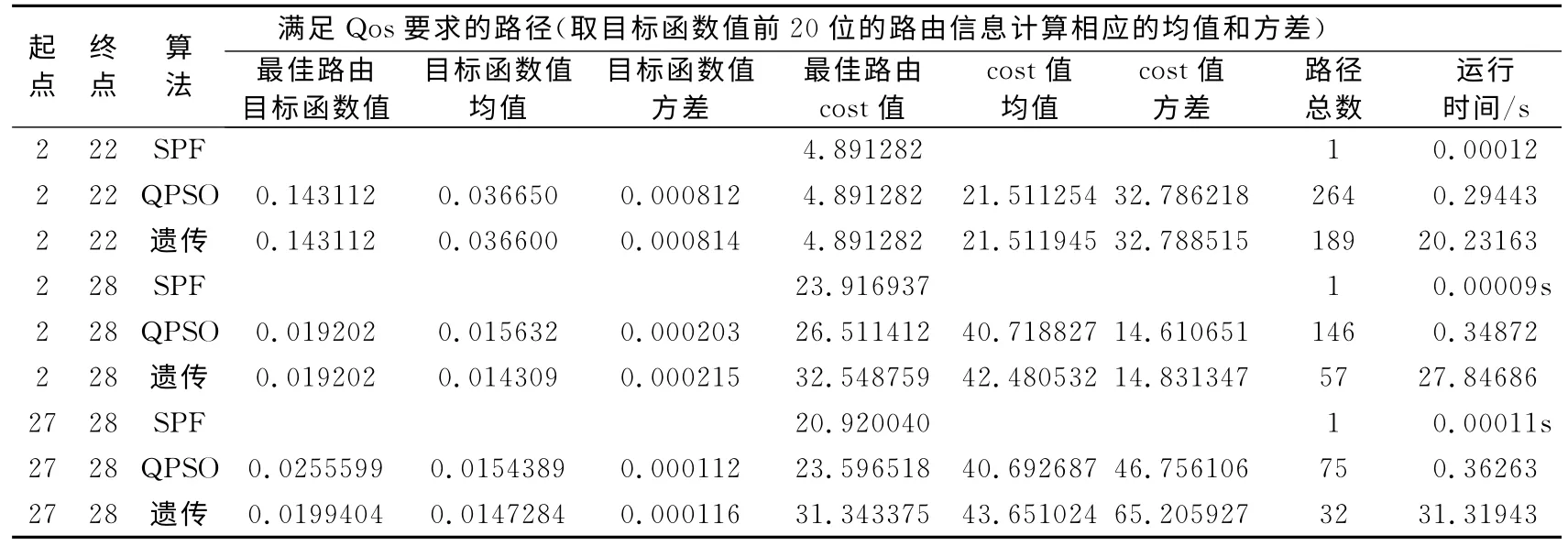
表2 QPSO与遗传算法的几组运行结果Tab．2 Several groups of the operation results of QPSO algorithm and genetic algorithm

表1的仿真结果表明：在相同时间内（112s），网络主要节点发送和接收的平均速率QPSO和遗传算法都比SPF明显提高，并且QPSO算法高于遗传算法．提高的主要原因是：SPF中的数据包在连续两次运行SPF期间始终沿前一次求得的唯一最优路径发送，由于网络链路性能时刻在动态变化，重新运行SPF之前原最优路径的性能很可能变得很差，很显然这种做法不合理．QPSO和遗传算法能够很好地解决SPF的这种不合理现象，解决方法是一次运行算法求得最优路径和多条次优路径，当前路径性能一旦发生明显恶化就立刻选取相对次优的路径而不必等到下一次运行算法重新路由，这样相对次优路径上的网络资源就得到了有效的利用．这说明在性能参数动态变化的OSPF网络中，为了满足Qos要求，快速改变路径是必要的．

表2的测试结果表明：QPSO与遗传算法相比，找到的最佳路由目标函数值大多数相同，少数较优，但次路由的目标函数值均值较大方差较小；其次，最佳路由cost值比较接近SPF，而且次路由cost均值和方差都较小；此外，满足Qos要求的路径数量明显较多，运行时间明显较短；SPF只搜寻一条最佳路径，计算时间显然最短．这说明QPSO算法的搜索能力较强、计算的时间复杂性较小，比较适宜解决多约束OSPF网络路由规划问题．

7 结 论

本文重点阐述了QPSO算法在OSPF网络路由选择中的具体应用，同时比较了QPSO算法、遗传算法和SPF算法的运行结果，通过对比分析可以得出如下结论．

在满足Qos要求的多约束OSPF网络路由选择中，与SPF算法相比，QPSO与遗传算法能够很好地利用相对次优路径上的网络资源，从而提高网络性能；与遗传算法相比，QPSO算法具有搜索能力强、运行效率高等优点．说明QPSO算法在满足Qos要求的OSPF网络路由选择领域中具有很好的应用前景，值得进一步深入的研究．

［1］王小明，卢俊岭，李英姝，等．模糊随机环境下的无线传感器网络多约束多路径路由［J］．计算机学报，2011（5）．

［2］SUN J，XU W B．A global search strategy of quantum－behaved particle swarm optimization［C］／／IEEE Conference on Cybernetics and Intelligent Systems．2004：111－116．

［3］SUN J，FENG B，XU W B．Particle swarm optimization with particles having quantum behavior［C］／／Proceedings of 2004 Congress on Evolutionary Computation．2004：325－331．

［4］魏娟．基于遗传算法的OSPF路由研究［J］．科技咨询，2013（22）．

［5］WANG X M，ZHANG Z，RAN C S．A rerouting strategy in lowearth orbit Qos sattllite networks［J］．Journal of Beijing University of Postsand Telecommunication，2005，28（1）：30－34．

［6］SCHMITT L M．Theory of genetic algorithmsⅡ［J］．Theoretical Computer Science，2004：181－231．