基于综合主成分模型的城市土壤重金属空间分布与传播特征研究

蒋诗泉，刘中侠，蒋诗平

（1．铜陵学院 数学与计算机科学学院，安徽 铜陵 244000；2．南京航空航天大学 经济与管理学院，南京 210016；3．中国科学技术大学 国家同步辐射实验室，合肥 230029）

0 引 言

城市化是中国发展的必然趋势，而在城市生态环境中，城市土壤是一个重要的组成部分，是连接食物、空气和水的重要纽带．人们的生产和生活都会将重金属带入土壤中，造成重金属在土壤中大量积累，为了有效地控制这种情况继续发生，必须要探明重金属污染的原因和传播途径．由此可以加深对城市重金属污染时空变异规律和变异机制的深入了解［1］，为合理规划和利用土壤，控制污染及改造和提高环境质量，保障人类健康提供重要依据．有学者将主成分法和因子分析法用于土壤重金属源的解析中［2］，但是这个方法的解析结果是总体上分析而得，反映的是总体情况，对各元素的来源判断是有限的，必须要结合各元素分布特征和周围情况作出判定．也有学者将人工神经网络（artificial neural network，缩写ANN）并结合3S技术对重金属空间动态分布进行研究［3］．人工神经网络的优点，是将土壤位置不同的空间点与该点处的重金属含量和污染程度之间的复杂的非线性关系建立网络模型，从而预测其他点的重金属含量和空间分布特征，但是该方法的本质是一种“黑箱”建模工具．因此，预测的空间分布精度的稳定性不能保证．赵志忠等采用现场采样及室内分析测试方法，对某地土壤剖面淋溶层、淀积层和母质层中7种重金属元素的分布特征进行研究，研究重金属与淋溶层、淀积层和母质层之间的关系［4］．由于该方法的土壤取样全是农业土壤，分析了其中的重金属元素含量及其分布特征和迁移富集规律，这些分布特征和迁移规律对城市地区重金属是否适应并不清楚．马志宏等利用傅里叶变换方法对重金属扩散模型及污染源位置进行了研究［5］．傅里叶变换主要是对原始数据进行预处理，这样可以将信号的低频段和高频段分开处理，主要是防止采集的数据本身带来误差而不能反映问题的本质．但是，对高频段部分应该根据具体情况有不同的处理方法，如果不根据实际情况而主观地采用某种处理方法，同样会造成预测精度不高的现象．刘文斌等用地累积指数法定量分析重金属污染程度及迁移规律的优化模型［6］．何用和李义天对重金属迁移转化模型进行了研究［7］，该研究是根据水沙运动与污染物相互作用关系，以及泥沙颗粒运动及重金属吸附解吸不平衡过程，同时结合水沙数学模型，建立了重金属迁移转化的耦合模型．但是该模型只是在理论上对重金属迁移转化进行了深入探讨，由于缺乏重金属迁移转化的实测资料，对模型能否在天然河流中应用没有进行进一步研究．近年来我国学者也关注城市重金属的来源、空间分布特征及其传播特征．吴新民等对南京市不同功能区的重金属污染特征进行了研究［8］，研究结果表明城市重金属污染较为严重，且不同的功能区之间存在明显差异．卓文珊以广州市城区土壤为研究对象，对不同土地利用背景下的7个功能区和5种重金属元素含量和形态以及重金属与土壤性质的关系进行了初步研究［9］．文献［8，9］的研究不足之处是对不同功能区的采样太少，这样将会影响所得结果的精度．柳云龙等采用地统计学方法对上海市表层土壤重金属的空间变异结构和分布格局进行了研究［10］，研究结果表明土壤重金属污染城郊乡梯度差异明显，工业化、城市化与城市土壤重金属空间分布密切相关．

本文在综合分析各类方法的基础上，对某个城市的不同功能区进行土壤采样，利用X射线荧光光谱仪测试其8种重金属的含量．将主成分分析法与微分方程方法进行集成，并利用SPSS和Matlab软件编程，探明As等8种重金属污染的原因及污染的空间分布和传播特征．为合理利用和保护城市的土壤资源以及工业企业的选址和城市发展规划提供科学的决策依据．

1 材料与方法

1．1 实验仪器与设备

实验使用英国牛津仪器公司的X－MET5000手持式X射线荧光光谱仪．工作原理是将样品通过X荧光射线进行激发，样品吸收X射线能量，然后发射出二次X射线．每个化学元素发射出的X射线都有其特有的能量．通过测量由此发射的X射线强度和特征能量，得到对被测材料的物质成分进行定性和定量分析．

1．2 实验样品的来源

对某城市进行功能区划分，共计分5个功能区，按每0．5 km2一个采样点对表层土壤（0～10 cm）进行取样并编号，同时通过GPS给采样点进行坐标定位．从而获得每个样本点土壤的多种化学元素及其As、Cd、Cr、Cu、Hg、Ni、Pb、Zn 8种重金属元素的浓度．对每0．5 km2取样基本上能够较为全面的反映一个地区的重金属分布及其污染情况，具有较高的可靠性．同时通过X－MET5000手持式X射线荧光光谱仪测试各种重金属的化学浓度有较好准确度和精密度．

1．3 数据处理及统计分析方法

数据采用SPSS 17．0软件和Matlab编程进行综合主成分分析模型的相关数据处理．

2 结果与讨论

考虑到每种元素浓度都在不同程度上反映了所研究问题的某些信息，并且各指标之间有一定的相关性，因此所得统计数据反映的信息在一定程度上可能会有重叠．为了全面地、系统地分析问题，本文建立综合主成分分析模型，通过对各功能区8种重金属元素的综合主成分分析，得出各功能区重金属污染显著的元素，从而能够获取各功能区重金属污染的主要原因．

2．1 主成分分析原理

2．1．1 单项主成分模型［11，12］

现以p个指标反映客观对象的各个特征，因此，每个对象观察到的p个指标值就是一个样本值·用矩阵X表示观察的n个对象，则

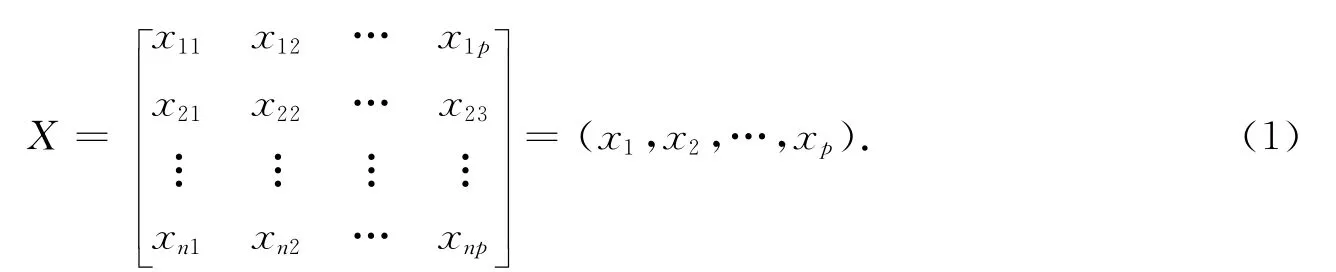
矩阵X中每一行就是一个样本的观察值，可用数据矩阵X的p个向量作线性组合为：

F1＝a11x1＋a21x2＋…＋ap1xp，

F2＝a12x1＋a22x2＋…＋ap2xp，

……

Fn＝a1nx1＋a2nx2＋…＋apnxp·

在解决实际问题时，一般不是取p个主成分，而是根据累计贡献率的大小取前k个．前k个主成分的累计贡献率定义为（λ1＋λ2＋…＋λk）／（λ1＋λ2＋…＋λp）．如果前k个主成分的累计贡献率达到某个给定值（85%），则表明取前k个主成分基本包含了全部测量指标所具有的信息，这样既减少了变量的个数，又便于对实际问题进行分析和研究．

2．1．2 综合主成分模型

综合主成分模型是以每个主成分所对应的特征值占所提取主成分总的特征值之和的比重作为权重，将各单个主成分加权而得来的．构造综合主成分模型主要目的是避免单项主成分模型的某些不足，如果按照单项主成分分析模型，第一主成分值与第二主成分值的排名差别可能较大，其原因是不同的主成分反映样本信息的侧重点不同，且第一主成分含有较多的信息．按照构造综合主成分模型的规则它应该占有较大的比重．同时，由于各主成分反映信息侧重点不同，第二主成分又会修正第一主成分在综合主成分模型中的排名．由此，得到的主成分值的含义就是在确定的信息提取规则下的综合贡献值．

综合主成分模型表达式为：

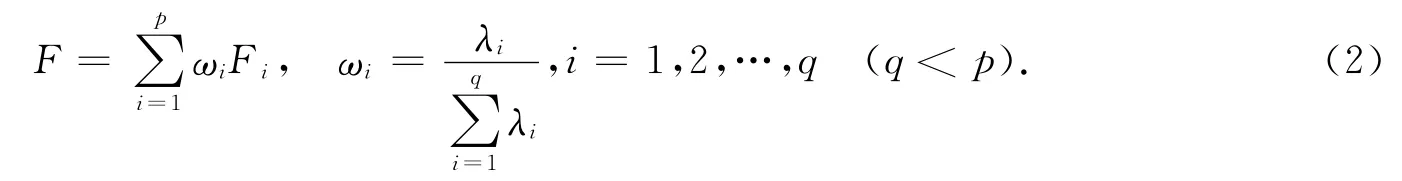
上式转换成以各原始因子为变量的贡献率为系数的综合主成分模型表达式：

比较综合主成分模型表达式的系数v1，v2，…v8，可以判定该地域污染程度较为显著的重金属元素种类．

2．2 本文模型求解及分析（以生活区为例）

由Matlab编程计算主成分贡献率以及累计贡献率可以写出主成分表达式：

F1＝0·669 5x1＋0·438 6x2＋0·350 8x3＋0·344 1x4＋0·105 3x5＋0·175 4x6＋0·281 5x7＋0·190 6x8，

F2＝1·153 6x1－0·171 4x2－0·227 9x3＋0·207 8x4－0·049 7x5＋0·115 5x6－0·070 4x7－0·469 8x8，

F3＝0·017 5x1＋0·428 7x2－0·492 9x3－0·021 1x4＋0·171 2x5－0·245 5x6＋0·223 6x7－0·186 2x8，

F4＝0·274 8x1－0·273 0x2－0·105 0x3－0·267 9x4＋0·318 7x5＋0·136 0x6－0·214 4x7＋0·096 7x8，

F5＝－0·766 5x1－0·533 3x2－0·203 4x3＋0·099 6x4＋0·036 2x5＋0·163 6x6＋0·418 7x7－0·102 9x8，

F6＝－0·962 9x1＋0·559 1x2－0·159 4x3＋0·075 8x4＋0·007 6x5＋0·246 9x6－0·206 0x7－0·208 8x8·

由

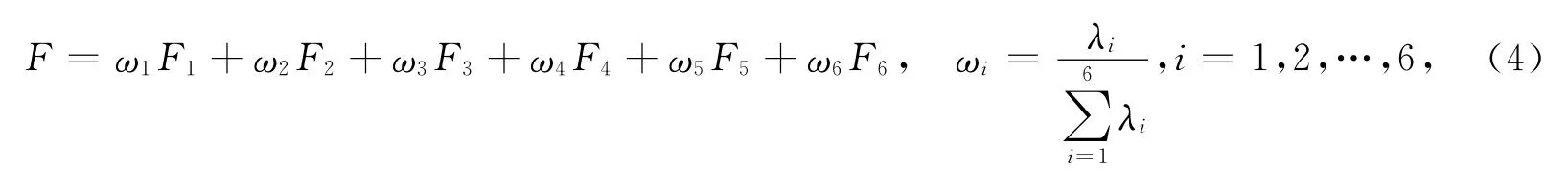
运行Matlab编制的功能函数，输出综合主成分模型系数表（见表1）．由表1数据可以得出生活区对应的综合主成分分析模型：

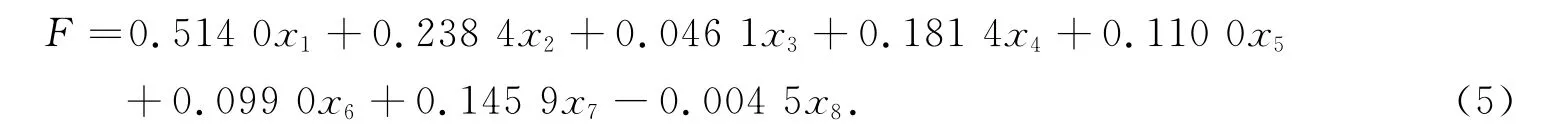
分析式（5）中系数知，对生活区污染程度贡献大小顺序为：As＞Cd＞Cu＞Pb＞Hg＞Ni＞Cr＞Zn．而且As元素对生活区污染程度贡献最大，Zn元素对生活区污染程度贡献最小．

同理，根据式（5）并结合测量的数据，可以得出其他4个功能区重金属元素对该区污染程度贡献大小顺序．①工矿业区：As＞Cr＞Cd＞Zn＞Ni＞Cu＞Hg＞Pb；②山地区：Cr＞Ni＞Cu＞Zn＞Hg＞Pb＞As＞Cd；③主干道路区：Hg＞Pb＞Cd＞Ni＞Cu＞Cr＞Zn＞As；④公园绿地区：Hg＞Pb＞Zn＞Cu＞Ni＞Cd＞Cr＞As．

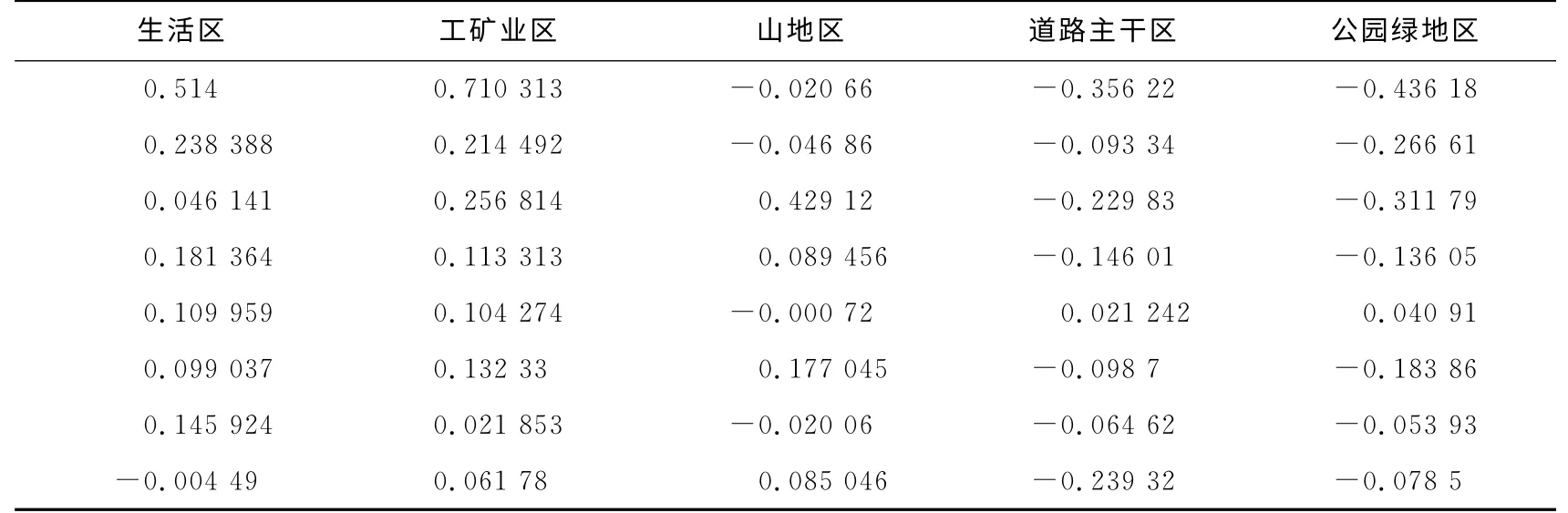
表1 5个功能区主成分分析综合模型系数Tab．1 Five functional areas coefficient of principal component analysis model

2．3 重金属污染的空间分布与传播特征分析

2．3．1 三维的非线性多项式拟合

分析8种重金属元素背景值的取值范围，结合统计学原理，可知其浓度随空间变化分布符合正态模型［13］．根据实测数据，为了达到既能体现8种重金属元素随海拔高度的分布状况，又能体现其在该空间位置浓度分布特征的目的，拟采用Matlab绘制四维表现图，即通过mesh（x，y，z，Con）语句（辅以colorbar命令）来绘制三维“地貌特征图”，其中输入参数项“Con”（concentration）是重金属的采样浓度（需注意的是，一般曲面作图是以曲面高度作为着色参数的）．这样，既保持了几何地貌的原型，又体现了重金属浓度的空间分布状况．在此，将以As元素为例，为说明其空间分布特征（将其三维图放大，见图1），同时也将其分布图投影到平面上作为其空间分布图（见图2）．通过图2，可以很清楚地看到As元素的覆盖面较广，几乎覆盖了整个城区，并且在西南部的浓度总体较高．在点（5 000，7 000）、（13 000，3 000）、（19 000，10 000）3个点附近浓度更是尤为突出，比整个城区其他地方的As浓度都要明显高出很多．再通过图1，则可以更加直观地看出，该城区平原区域地表土壤中As的浓度明显高于山地地区，而且还能够看出在图1中浓度较为突出的3个点在地表的分布状况，即一处分布于海拔较低的低洼处，而另两处则分布在两个小山坡上．可见，用二维表现图与四维表现图相结合的方式，来描述8种重金属元素的空间分布非常形象、直观，这是等高线图或单纯用平面分布图所无法到达的效果．另外，其它7种元素三维图列于下方，便于观察其空间分布特征（统一称图3）．

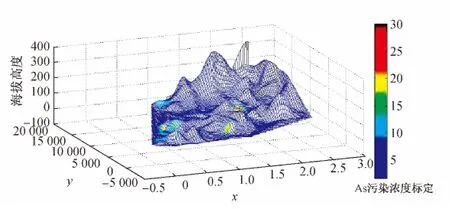
图1 As元素在该城区三维地貌上的分布状况Fig．1 The distribution of the three－dimensional landscape of the As elements in the urban areas

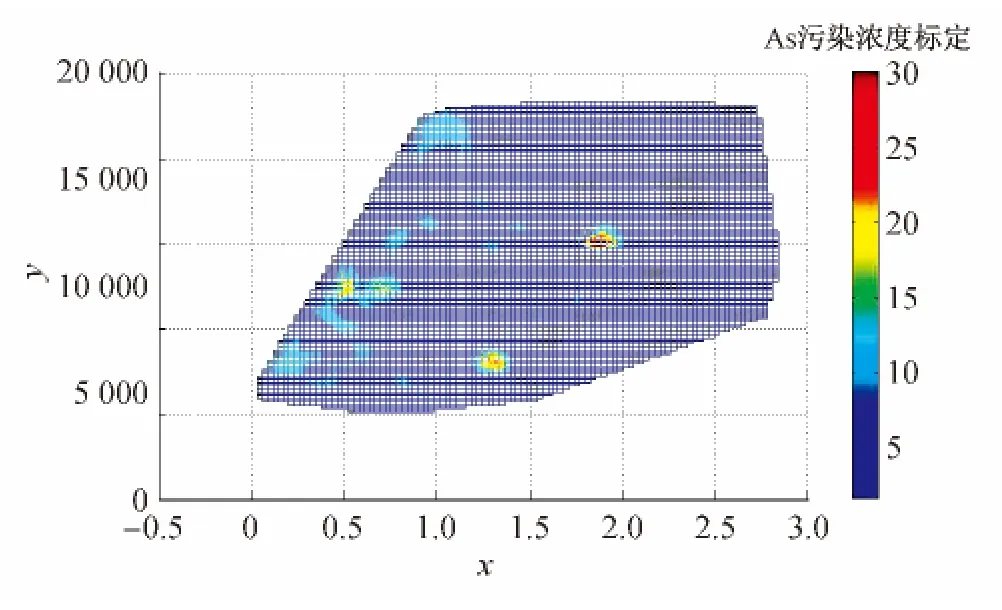
图2 As元素在该城区的空间分布状况Fig．2 The spatial distribution of the As elements in the urban area

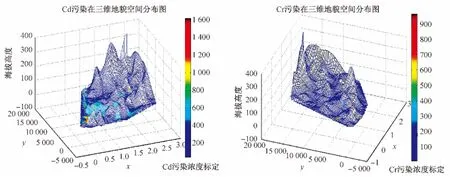
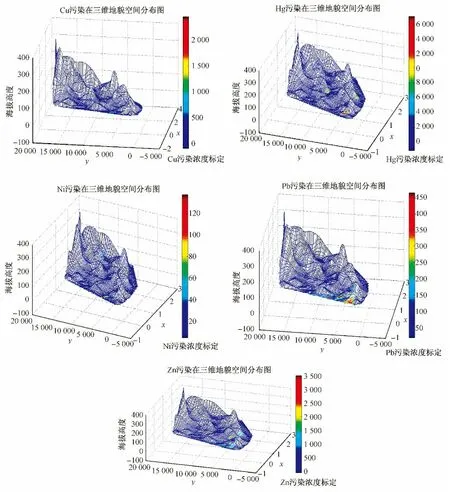
图3 Cd、Cr、Cu、Hg、Ni、Pb、Zn元素在该城区三维地貌上的分布状况Fig．3 The distribution of the three－dimensional landscape of the Cd、Cr、Cu、Hg、Ni、Pb、Zn elements in the urban areas

为了详细说明图3中重金属的在该城区的三维地貌上的分布情况，首先，引入一个三维数组表示式（x，y，z）．其次，结合三维地貌图和GPS的定位图分别对重金属污染进行空间分布特征说明．Cd的空间分布特征：在坐标（6 869，7 286，19）、（7 056，8 348，37）、（7 747，8 260，49）、（26 086，10 799，53）、（26 015，12 078，57）、（27 700，11 609，165）、（27 346，13 331，100）、（27 696，11 621，169）在这些点处Cd的污染比较严重，它们主要集中在生活区，这些点处的海拔相对较低．而在（13 175，12 238，31）、（13 277，13 204，19）、（14 269，12 877，27）这些点处污染相对较轻，且这些点处海拔不高．而在其他地区重金属Cd的污染非常小甚至几乎没有污染．再结合空间分布图分析，可以发现Cd在该城区有多个富集点，其浓度在由富集中心向外扩散过程中逐渐减小；另外，可以看出在东部地区有一个富集点时，周边的浓度就小，而在西部有多个点时，其周边的浓度就大，从而说明该元素容易扩散．Cr的空间分 布 特 征：在（10 630，8 774，29）、（10 700，8 184，50）、（11 902，7 056，37）、（11 678，8 618，37）、（21 006，8 618，17）这些点处污染较为严重，海拔在40 m左右．而且这个污染点位于城市西南角处，由污染点处向四周扩散时其浓度逐渐减小，其他地方污染很小．Cu的空间分布特征：在（22 624，4 818，27）、（23 359，5 325，28）、（21 703，6 591，65）这些点处相对污染较重，同时可以看出主要是集中在山区，而在（22 176，5 492，25）这个点处污染较轻，其他点处几乎没有污染．这说明Cu的扩散很小．Hg的空间分布特征：在（10 685，5 528，34）、（10 631，6 472，57）、（10 643，4 472，45）、（21 418，10 721，35）、（21 439，11 388，45）、（21 439，11 383）、（19 501，6 099，9）、（21 018，5 764，9）坐标处污染较为严重，可以看出这些点都位于交通主干道区，由污染点中心向外扩散，浓度逐渐降低．而在其他地区几乎没有污染且浓度分布均匀．Ni的空间分布特征：在（12 746，8 450，21）、（12 855，8 945，18）、（13 799，9 621，18）、（11 902，7 709，30）这些点处污染相对较重且海拔较低，也主要集中在山区和交通主干道区，由污染中心向外扩散时浓度逐渐减少，而在其他地区几乎没有污染．Pb的空 间 分 布 特 征：在（12 442，4 329，65）、（13 093，4 339，56）、（13 244，7 056，57）、（12 778，5 799，93）、（11 702，4 480，71）这些点处污染相对较重，海拔一般大约在50～90 m之间，从三维地貌图可以看出其他相对较轻的污染地区海拔也不高，都在100 m以下的地区．但是这些污染点任然集中在交通主干道区．同时从空间图可以看出Pb污染点集中在西南部，并且西南部的浓度高于东部城区．Zn的空间特征分布：在（16 569，6 055，78）、（16 387，6 609，44）、（16 061，7 352，28）、（15 092，6 936，32）这些点处污染较为严重；而在（11 730，5 332，54）、（11 482，6 354，61）、（11 702，4 480，71）、（21 018，5 764，9）、（23 359，5 325，28）、（22 624，4 818，27）、（23 238，6 502，169）这些点处污染相对较轻，在其他处几乎没有污染．而且主要污染点集中在城区的西南部，但是向外扩散范围小且由污染中心向外扩散其浓度也是逐渐减小．

2．3．2 空间分布的正态模型

根据各重金属的空间分布特征的分析，同时结合三维地貌图和污染点的坐标来拟合它们的空间分布模型．从以上各元素的空间特征分析可以看出，各种重金属分布都存在一定的区域性，并且都是由污染中心（富集中心）向四周扩散，在扩散过程中其浓度逐渐减少，在富集中心较远的区域浓度较小且比较稳定．另外，各金属扩散的范围大小不一，说明不同重金属的扩散能力不一样．在此仅以As元素为例来说明问题，空间图见图1．As元素的分布特征，首先，该元素在该城区具有明显的富集现象，且主要集中在城市的中部地区，这一地区污染也是最严重的；其次，污染较为严重的地区是该城市的西南部和南部地区；最后，从空间图可以看出城区的其他地区分布较为均匀．该元素的最大特点是由中心向四周扩散，并且浓度也逐渐降低．按照同样的方法对其他元素进行分析，结论是：总体而言这些元素的空间分布主要呈现近似的正态分布，有的元素分布特征比较复杂，一般可能呈现偏正态分布．为此，通过对各重金属元素浓度随空间分布的立体图形的观察，建立浓度随空间分布的正态模型［14］：

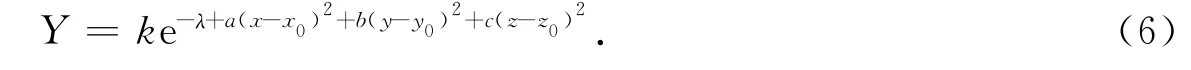
对方程（6）进行线性化处理得，

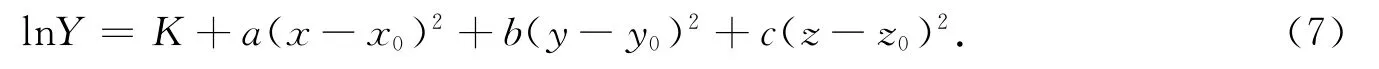
其中，自变量x、y、z为地域的三维坐标；lnY是对应的坐标下重金属元素浓度的对数值；K、λ、a、x0、b、y0、c、z0为模型的系数．

通过Matlab编写功能函数chuanbo．m拟合，求解出以上7个参数的值．其中，a的代数意义是三维正态分布中沿x方向某种重金属元素浓度值2倍标准差的倒数，同理b，c分别表示沿y轴和z轴方向某种重金属元素浓度值2倍标准差的倒数．而λ是表示不沿任何方向时的某种重金属元素浓度值2倍标准差的倒数．得通过比较系数a，b，c，便可以得出三维坐标系中的显著性变化的方向．则某种重金属元素浓度最大值的分布点即为（x0，y0，z0）处，结合图形分析出该元素是以“外来汇集”，还是“源头发散”的传播特征传播（若在山顶或在山坡处浓度最大，该元素以“源”的方式向外传播即此点是该元素污染的污染源；而在低洼处浓度最大，则既可能是污染源也可能是汇集地，需要根据a、b、c的数值进行判断）．

2．3．3 传播特征方程

若判定某点为污染源，则将公式（7）转化为正态分布方程形式，即该重金属污染物的传播方程为

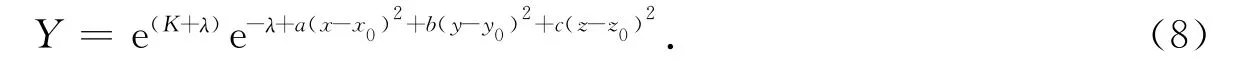
公式（8）中的参数意义同公式（7）．通过拟合的数据处理技术编写Matlab程序chuanbo．m，得到各功能区模型系数值．

现在以第一功能区（生活区）As元素的传播特征为例进行分析说明，其他各区各元素传播特征分析可根据表1中参数依此类推．

以As元素为例，第一功能区各重金属元素的浓度随空间分布函数为

Y＝5－2·079 253 161 794 13×10－9×（x－1）2＋1·014 255 935 330 12×10－8×（y－1）2＋0·000 293 091 701 285 808×（z－1）2·

（x，y，z）＝（1，1，1）的点在空间中海拔位置较低，且在周边的As浓度随海拔的升高呈现出辐射状下降的趋势，可见此处As元素的传播特征是周边As元素向此处聚集回笼．由此可见，在第一功能区中（1，1，1）的位置处As元素含量最高，但并不是As元素的污染源．再结合对图1的观察，可知在该区域附近海拔较高处，且现实浓度值较大的空间位置是As元素的实际污染源．而且，由方程可以看出c的值明显大于a、b的值，这说明海拔高度对其传播速度的影响非常显著，对城市规划和环境治污的启示是As工业的选址应该在海拔较低处．

3 结 论

本文通过建立主成分分析法模型，对每个功能区的重金属污染做定量的分析．并且对每个功能区中8种重金属对该区污染的贡献做了排序，从而找到了“引起污染的主要原因”，结合文献资料，可以看出所得到的结论也是较为准确的．①生活区：引起重金属污染的主要元素是As和Cd，影响显著较小的是Cr和Zn；②工业区：引起重金属污染的主要元素是Cr和As，影响显著较小的是Ni和Pb；③山区：引起重金属污染的主要元素是Cr和Ni，影响显著较小的是As和Cd；④主干道路区：引起重金属污染的主要元素是Pb和Hg，影响显著较小的是Zn和As；⑤公园绿地区：引起重金属污染的主要元素是Pb和Hg，影响显著较小的是Cr和As．

根据统计数据描绘出重金属污染空间分布四维直观图，由其构建其空间分布特征和传播方程，也就找到了各重金属污染的“源”．该问题的研究结论给当地政府和环境保护主管部门在做决策时提供比较科学的根据，同时也为土地管理规划部门在科学合理用地时作为环境因素的一个重要参考．

［1］蒋诗泉．模糊数学方法及X射线荧光分析技术在测定城市重金属污染中的应用［J］．光谱实验室，2012，29（4）：2135－2139．

［2］林燕萍，赵阳，胡恭任，等．多元统计在土壤重金属污染源解析中的应用［J］．地球与环境，2011，39（4）：536－542．

［3］胡大伟，卞新民，许泉．基于ANN的土壤重金属分布和污染评价研究［J］．长江流域资源与环境，2006，15（4）：475－479．

［4］赵志忠，RATE A W，唐少霞，等．海南岛农用地土壤重金属元素的空间分布特征及其环境意义［J］．农业环境科学学报，2007，27（1）：182－187．

［5］马志宏，穆安冬，宫明．基于傅里叶变换的重金属扩散模型对污染源位置的研究［J］．安徽农业科学，2013，41（11）：5014－5015．

［6］刘文斌，刘欢，刘雅晴，等．土壤污染程度分析及迁移规律的优化模型［J］．数学理论与应用，2012，32（2）：91－96．

［7］何用，李义天．重金属迁移转化模型研究［J］．水科学进展，2004，15（5）：576－583．

［8］吴新民，李恋卿，潘根兴，等．南京市不同功能城区土壤中重金属Cu、Zn、Pb和Cd的污染特征［J］．环境科学，2003，24（3）：105－111．

［9］卓文珊，唐建锋，管东生．广州市城区土壤重金属空间分布特征及其污染评价［J］．中山大学学报：自然科学版，2009，48（4）：47－51．

［10］柳云龙，章立佳，韩晓非，等．上海城市样带土壤重金属空间变异特征及污染评价［J］．环境科学，2012，32（2）：600－605．

［11］蒋诗泉．基于PCA和LS－SVM的傅里叶变换近红外光谱的黄酒酒龄的鉴别模型研究［J］．光谱实验室，2012，29（2）：806－810．

［12］王从陆，吴超，段瑜．基于主成分综合的矿区农田重金属污染评价［J］．中国工程科学，2008，7（10）：181－182．

［13］王学松，秦勇．利用对数正态分布图解析徐州城市土壤中重金属元素来源和确定地球化学背景值［J］．地球化学，2007，1（36）：98－102．

［14］SIEGAL F R．Environmental Geochemistry of Potentially Toxic Metals［M］．Heidelberg：Springer，2002：1－192．