二阶差分方程组周期解的多重性
郭 娟,陈 丽,张建明
(1.山西工商学院 基础教学部,山西 太原030006;2.太原理工大学 数学学院,山西 太原030024)
1 引言及主要结果
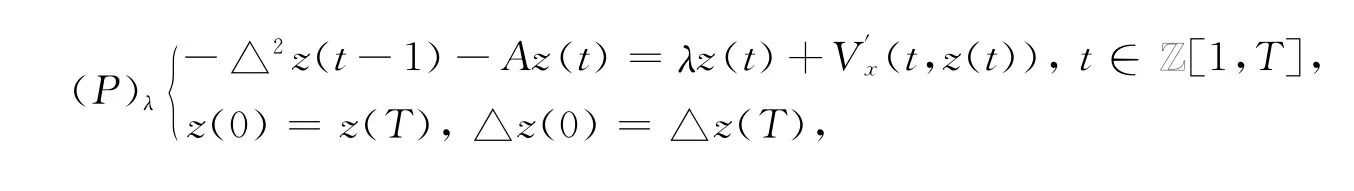
众所周知,非线性差分方程(组)已广泛应用于研究计算机科学、经济学、神经网络、生态学及控制论等学科中出现的离散模型.因此,关于差分方程的可解性、稳定性、周期性及振动性等问题的研究被许多学者所关注.就非线性共振差分方程的可解性而言,人们主要利用Morse理论和变分方法等来研究差分方程解的存在性与多重性[1-8].
本文主要讨论下列二阶差分方程组周期解的多重性.这里的λ是一个实参数,A是R2上的对称矩阵,T≥2是一个给定的整数,当a,b∈Z且a≤b时,Z[a,b]={a,a+1,…,b},△是向前差分算子,即△z(t)=z(t+1)-z(t),△2z(t)=△(△z(t)),V∈C2(Z[1,T]×R2,R)且满足下列条件:
(V0)V(t,0)=0,V′x(t,0)=0,V″x(t,0)=0,t∈Z[1,T].
(V∞)存在¯R>0,α>2使得当‖x‖>¯R,t∈Z[1,T]时,0<αV(t,x)≤(V′x(t,x),x).
(V01)存在ε>0,使得当0<‖x‖<ε时,V″x(t,x)>0,t∈Z[1,T].
(V02)存在ε>0,使得当0<‖x‖<ε时,V″x(t,x)<0,t∈Z[1,T].
(V)对任意的p>α,存在M>0使得当x∈R2,t∈Z[1,T]时,|V(t,x)|≤M(1+‖x‖p).
其中,(·,·)和‖·‖分别为R2上的内积和范数.对任意两个R2上的对称矩阵B和C,当B-C是一个正定矩阵时,记为B>C.
由V′x(t,0)=0可知,对任意的λ∈R,z≡0是(P)λ的解,本文主要是寻找(P)λ的非平凡周期解.令λ1<λ2<…<λm是(P)λ相应的线性问题的所有互异特征值.记主 要 结 果 如下:
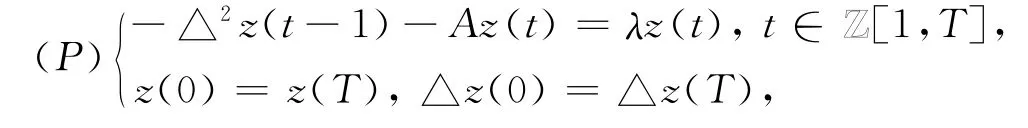
定理1 假设V满足(V0)-(V01)和(V),i∈Z[1,m-1],则存在δ>0,使得当M-≤δ,λ∈(λi-δ,λi)时,(P)λ至少有三个非平凡周期解.
定理2 假设V满足(V0),(V∞),(V02)和(V),i∈Z[1,m-1],则存在δ>0,使得当M-≤δ,λ∈(λi,λi+δ)时,(P)λ至少有三个非平凡周期解.
2 预备知识
ap‖z‖≤‖z‖p≤bp‖z‖,z∈E.(1)记C=B-A⊗IT,其中
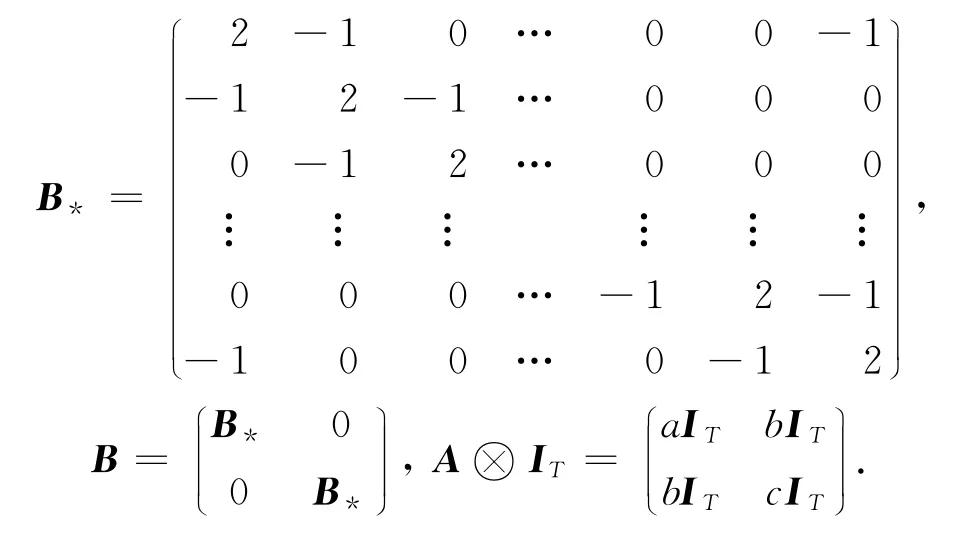
则J∈C2(E,R).且对任意z1,z2,z3∈E,有
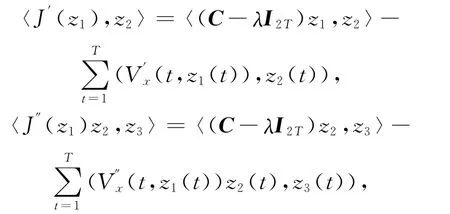
所以问题(P)λ的解等价于泛函J在E上的临界点.
对任意的i∈Z[1,m],定义

则E=Ei⊕E⊥i.记pi=dim E(λi),qi=dim Ei=设z0∈E是J的一个临界点,记μ(z0)和ν(z0)是J在z0处的Morse指数和零化度.
定义1 设E是一个Banach空间且J∈C1(E,R),若对任意{zn}⊂E,{J(zn)}有界且J′(zn)→0(n→∞)蕴含{zn}有收敛子列,则称泛函J在E上满足(PS)条件.
定义2[9-10]设E是Hilbert空间且J∈C2(E,R)满足紧性条件(PS),z0是J的一个孤立临界点且J(z0)=c,U是只包含临界点z0的邻域,则Cq(J,z0)=Hq(Jc∩U,(Jc\z0)∩U),q∈N∪{0},称为J在点z0处的第q个临界群,其中Jc={z∈E|J(z)≤c},Hq(A,B)为带有整系数的拓扑对(A,B)的第q个奇异相对同调群.
命题1[11]设E是一个Hilbert空间,Φ∈C2(E,R),且▽Φ(z)=Lz+H(z),其中L∈L(E,E)是对称的,且当‖z‖→0时,H(z)=o(‖z‖).考虑如下等式
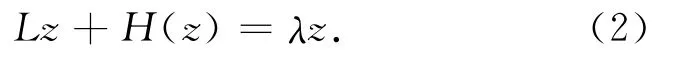
令μ∈σ(L)是一个有限孤立特征值,则下列结论之一成立.
(i)(μ,0)不是式(2)在μ×E上的一个孤立解.
(ii)存在一个μ的一侧的邻域Λ,使得对任意的λ∈Λ\{μ},式(2)至少有两个不同的非平凡解.
(iii)存在一个μ的领域Λ,使得对任意的λ∈Λ\{μ},式(2)至少有一个非平凡解.
命题2[10-12]设E是一个实的Banach空间,E=X⊕Y,l=dim X<∞.若J∈C1(E,R)满足(PS)条件,且满足
(J1)存在ρ>0,γ>0,使得当z∈Sρ=Y∩∂Sρ时,J(z)≥γ,其 中Sρ={z∈E|‖z‖≤ρ};
(J2)存在R>ρ>0和e∈Y,且‖e‖=1,使得当z∈∂Q时,J(z)<γ,其中Q={z=u+se|‖z‖≤R,u∈X,0≤s≤R}.
则J有一个临界点z0,满足J(z0)=c0≥γ,且Cl+1(J,z0) 0,这里的Sρ和∂Q是关于直和分解E=X⊕Y的一个同调环绕.
3 主要结果的证明
引理1 假设V满足(V∞),则对任意λ∈R,泛函J满足(PS)条件.
证明 设{zn}⊂E满足|J(zn)|≤M1(n∈N),且J′(zn)→0(n→∞),只需证明{zn}有界.取由假设,存在N∈N,则当n>N时,有
M1+β‖zn‖≥J(zn)-β〈J′(zn),zn〉.由(V∞)及连续性,存在M>0,使得
V(t,x)≥M‖x‖α-M,t∈Z[1,T],x∈R2. (3)
又V∈C2(Z[1,T]×R2,R),故存在D>0使得
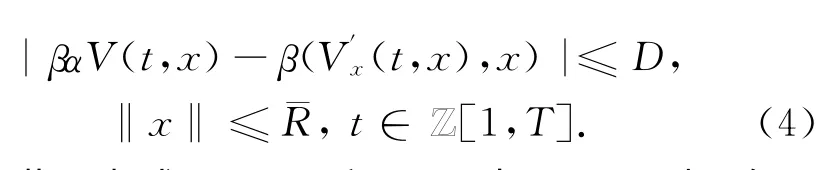
因此,由式(1),(3)和(4),当n>N时,有
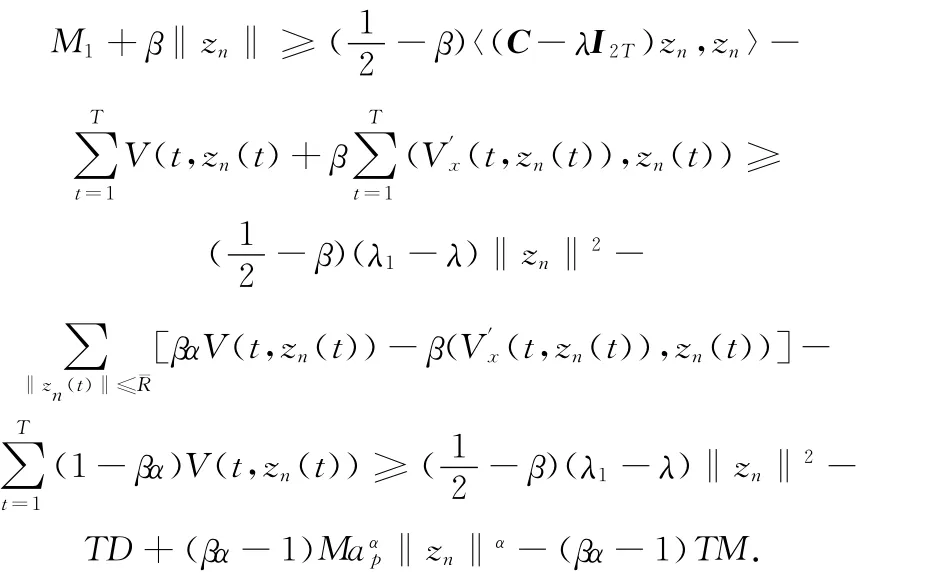
由于α>2,β∈(α ,2),则{zn}是有界的.
引理2 假设V满足(V0),(V∞)和(V),则对任意固定的i∈Z[1,m-1],存在ρi>0,γi>0,使得当λ<λi+1时,有
J(z)≥γi,z∈E⊥i,‖z‖=ρi. (5)证明 由(V0)和(V),对任意的ε>0,存在Mε>0,使得
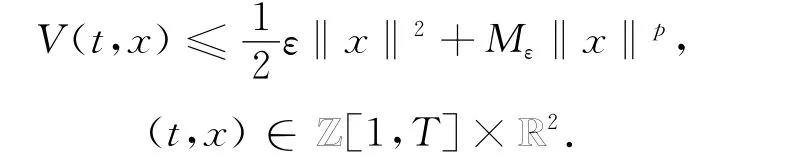
当z∈E⊥i时。由式(1)可知
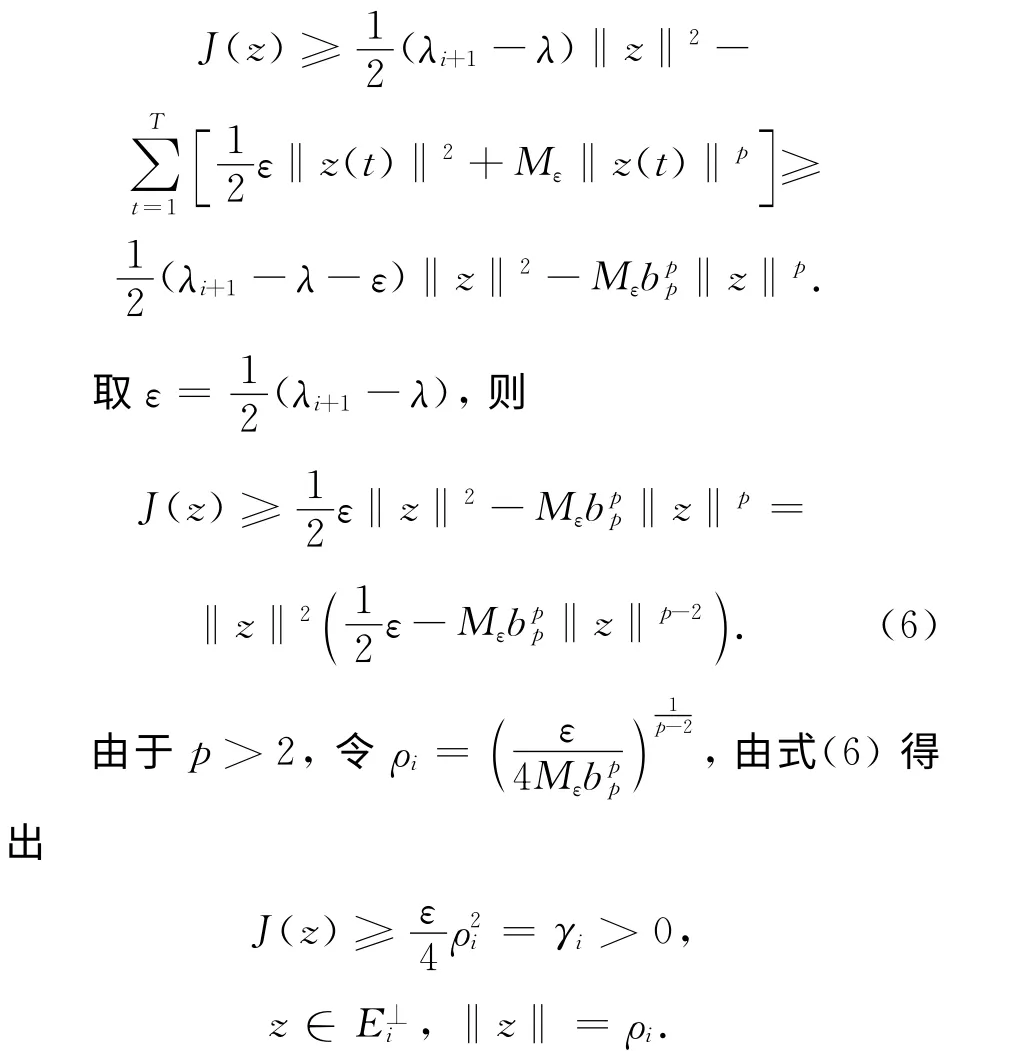
引理3 假设V满足(V∞),i∈Z[1,m-1],则存在R>0,0<δ<min{λi-λi-1,λi+1-λi}和σ∈R,使得当M-≤δ时,对任意固定的λ∈(λi-δ,λi+δ),有

这里λ0=0,Qi={z∈Ei⊕span{φi+1}|‖z‖≤R,z=u+sφi+1,u∈Ei,s≥0},φi+1是(P)相应于特征值λi+1的特征函数,且‖φi+1‖=1.
证明 对任意z∈Ei⊕span{φi+1),有z=u+v,其中u∈Ei-1,v∈E(λi)⊕span{φi+1},s≥0,由式(1)和(3)可得
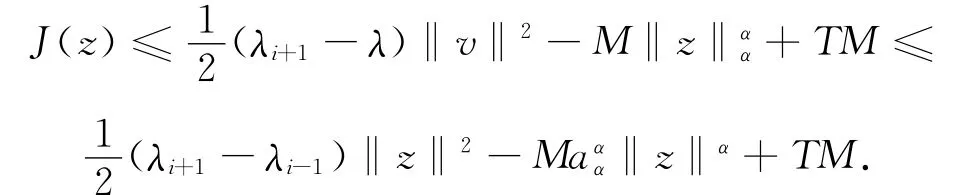
由于α>2,所以存在R>0使得
J(z)≤0,z∈Ei⊕span{φi+1},

对任意的u∈Ei,‖u‖≤R,有u=w+v,其中w∈Ei-1,v∈E(λi).当λ∈(λi-1,λi+1)时,有
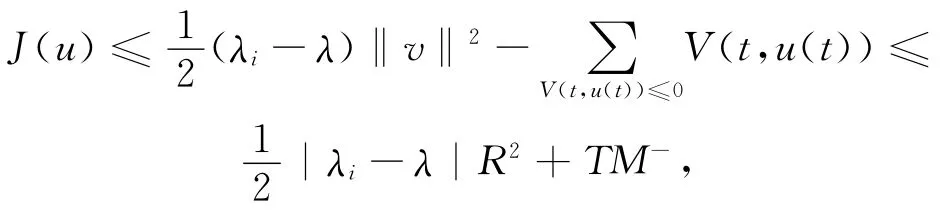
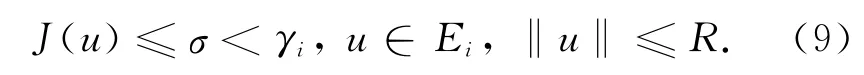
定理3 设V满足(V0),i∈Z[1,m],则存在δ>0,当V满足(V01)且λ∈(λi-δ,λi)或V满足(V02)且至少存在两个非平凡周期解,且解zλ的Morse指数和零化度满足

证明 利用命题1(ii)来证明解的存在,只证明V满足(V01)且λ∈(λi-δ,λi)的情形,另一种情形的证明是类似的.因为V满足(V0),(P)的每个特征值λi导致(P)λ的一个分歧点(λi,0)[11].令接近(λi,0)的一个解,且满足
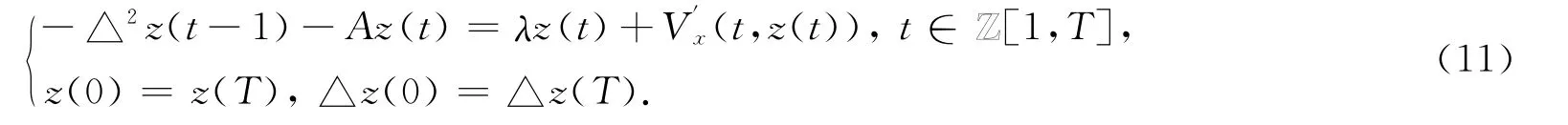
由(V0)有
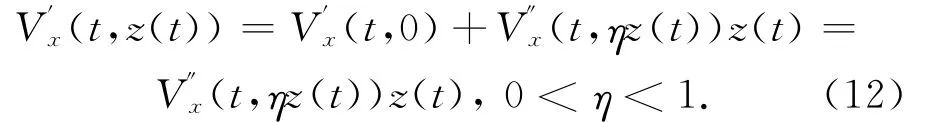
在假设条件下,由(V01)可知V″x(t,ηz(t))>0,t∈Z[1,T],则有A+V″x(t,ηz(t))>A,t∈Z[1,T].现在考虑线性方程组
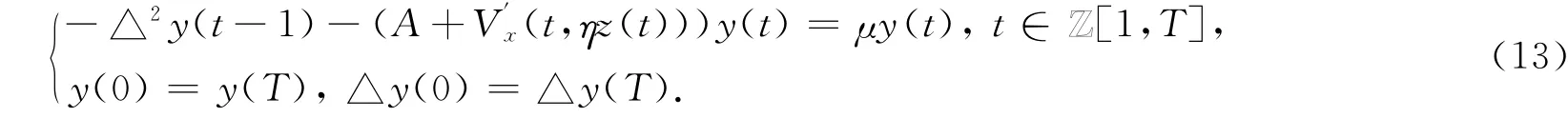
记μ1(z)<μ2(z)<…<μjz(z),z≠0为式(13)的所有互异特征值,根据条件(V0),若令z=0,则对每个k∈Z[1,j0]存在n∈Z[1,m]使得μk(0)=λn,因此式(13)的特征值μk(z)小于方程(P)相应的第n个特征值λn,并且当z→0时,μk(z)→λn,z∈E,由式(11)和(12)可知,z是式(13)的一个解,特征值为λ,且λ<λi.
下面估计Morse指数.令zλ是(P)λ的一个分歧解,当λ→λi时,‖zλ‖→0.对任意z1∈E有
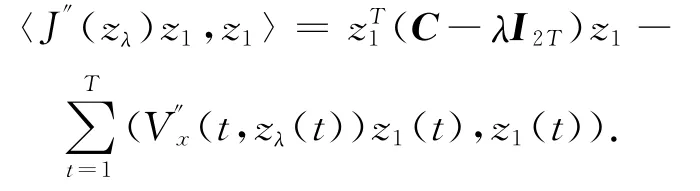
因此,当Z1∈Ei-1时有
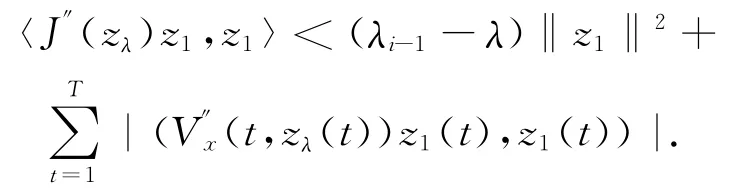
当z2∈E⊥i时有
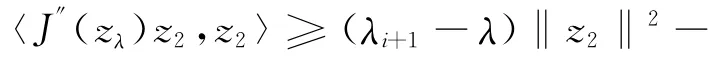

通过V0可知 存在δ>0使得0<|λ-λi|<δ时,
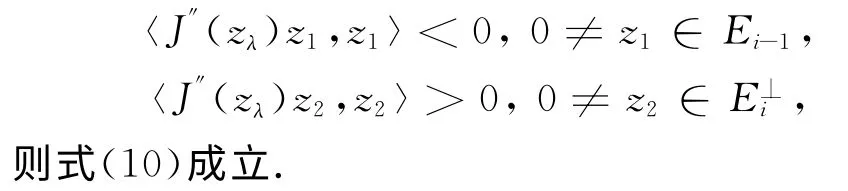
定理4 假设V满足(V0),(V∞),(V),i∈Z[1,m],则存在δ>0,使得当M-≤δ时,对第一个λ∈(λi-δi,λi+δ),(P)λ有一个非平凡周期解zλ,并且
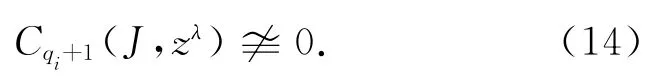
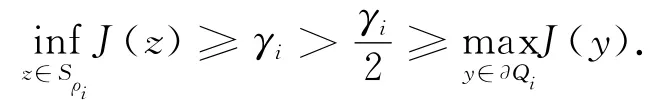
由引理1可知,J满足(PS)条件.当R>ρi>0,Sρi和∂Qi是关于直和分解E=Ei⊕E⊥i的一个同调环绕时,由命题2可知J有一个临界点zλ满足式(14).
定理1的证明 由定理3以及Gromoll-Meyer定理[10,13]可得到(P)λ有两个非平凡周期解它们的Morse指数满足
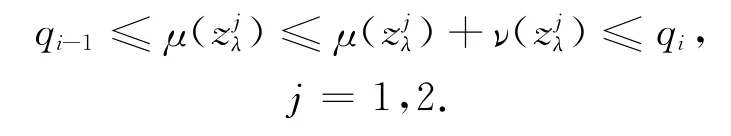
并且
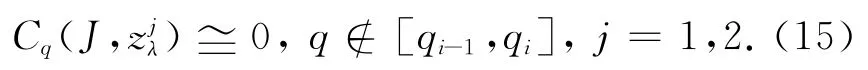
由定理4可知当λ∈(λi-δ,λi)时,(P)λ有一个非平凡周期解zλ满足

定理2的证明 与定理1的证明类似,λ∈(λi,λi+δ)时,应用定理3以及定理4可证得结论.
[1]Liu Jinsheng,Wang Shuli,Zhang Jianming.Nontrival solutions for resonant dierence systems via computations of the critical groups[J].J.Math.Anal.Appl.,2012,385:60-71.
[2]Zhang Guoqing,Liu Sanyang.Multplicity results for a class of second order superlinear dierence systems[J].Bull.Korean Math.Soc.,2006,43:693-701.
[3]Bin Honghua,Yu Jianshe,Guo Zhiming.Nontrivial periodic solutions for asymptotically linear resonant dierence problem[J].J.Math.Anal.Appl.,2006,322:477-488.
[4]Zheng Bo,Xiao Huafeng.Existence of multiple solution of a second-order dierence boundary value problem[J].Int.J.Math.Math.Sci.,2010:19-39.
[5]Liu Jinsheng,Wang Shuli,Zhang Jianming.Mulitiple solutions for boundary value problems of second-order dierence equations with resonance[J].J.Math.Anal.Appl.,2011,374:187-196.
[6]Wang Shuli,Liu Jinsheng,Zhang Jianming,et al.Existence of non-trivial solutions for resonant dierence equations[J].Journal of Dierence Equations and Applications,2013,19(2):209-222.
[7]郑波.共振条件下二阶差分边值问题多解的存在性[J].广州大学学报,2010,9(1):10-14.Zheng Bo.Existence of multiple solutions for second dierence boundary value problems with resonance[J].Journal of Guangzhou University,2010,9(1):10-14.(in Chinese)
[8]胡蓉晖,黄立宏.一类高阶差分方程周期解的存在性[J].应用数学学报,2008,31(3):492-499.Hu Ronghui,Huang Lihong.Existence of peeriodic solutions to a higher order dierence equation[J].Acta Mathematicae Applicatae Sinica,2008,31(3):492-499.(in Chinese)
[9]Mawhin J,Willem M.Critical point theory and hamiltonian systems[M].Berlin:Springer,1989.
[10]Chang K C.Infinite dimensional Morse theory and multiple solution problems[M].Boston:Birkhäuser,1993.
[11]Rabinowitz P H.Minimax methods in critical point theory with applications to dierential equations[M].USA:American Mathematical Society,1986.
[12]Liu Jiaquan.The Morse index for a saddle point[J].J.Systems Sci.Math.Sci.,1989,2(1):32-39.
[13]Gromoll D,Meyer W.On dierential functions with isolated critical point[J].Topology,1969(8):361-369.

