多中心的非平衡K-均值聚类方法
亓 慧
(太原师范学院 计算机系,山西 太原030012)
0 引 言
随着计算机技术和网络技术的迅猛发展,现实世界中需要处理的数据越来越复杂,《Science》及《Nature》等杂志近年来都聚焦大数据处理问题.如何从大规模的复杂数据中挖掘到人类需要的重要信息,成为人工智能乃至信息学科的一个重要研究课题[1-4].
作为一种最典型的数据挖掘任务,聚类已经得到了许多研究人员的广泛关注,并设计了多种针对不同类型数据的方法,如划分聚类[5]、层次聚类[6]、密度聚类[7]、网格聚类[8]、概率聚类[9]和谱聚类[10]等.
在这些聚类方法中,K-均值聚类是一种最为经典,使用最为广泛的划分聚类方法[11-14].其本质就是实现对数据的划分,使得划分后的数据类间的不相似度尽可能高,类内的相似度尽可能高.但是,对于非平衡数据的聚类问题[15],传统K-均值聚类方法往往容易将分布在区域较大类中的部分样本错误地划分到区域分布较小的类中,即在非平衡分布数据集上得到的聚类结果存在均匀效应.目前,已经提出了一些解决非平衡数据聚类的改进方法,如基于下采样的非平衡聚类[16]、基于密度的非平衡聚类[17]、基于熵的非平衡聚类[18]、基于鲁棒性的非平衡聚类[19]等方法,但这些方法往往是针对较为均衡的非平衡聚类或只有个别少数样本(如噪声问题)聚类问题的方法,对于传统非平衡数据的聚类问题,依然缺乏有效的解决方法.
本文针对K-均值聚类中存在的均匀效应现象,提出一种多中心的非平衡K-均值聚类方法,以消减非平衡分布数据聚类时产生的均匀效应.该方法通过对聚类结果中较大的类别进行二次聚类的方式对处于聚类模糊边界的样本进行划分,减小聚类均匀效应.
1 传统K-均值聚类及均匀效应
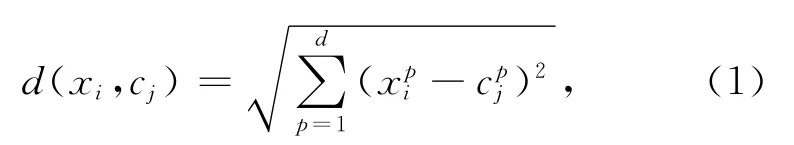
式中:xpi表示样本xi的第p个分量;cpj表示类心cj的第p个分量,新类心的更新如下

式中:xjq为第j类样本集的第q个样本;cj为第j类样本集的类心;nj为第j类样本集中包含的样本个数.反复循环迭代直到中心收敛为止.
但是,由于传统K-均值聚类方法仅根据样本与类中心的距离进行聚类,对于非平衡分布数据的聚类问题,传统K-均值聚类方法往往容易将分布在较大区域的类别的边界附近样本错误地划分到分布较小区域的类别当中,导致非平衡分布样本聚类过程产生均匀效应,得到错误的聚类结果.图1中,样本分布区域A明显大于样本分布区域B,从人类认知角度,显然聚为A区域样本和B区域样本更合适,但如果采用传统K-均值聚类方法则容易导致部分A区域中的样本错误划分到B区域所属类别当中,即产生均匀效应.本文通过引入多中心聚类的概念,构建模糊工作集,对其区域内样本进行二次聚类,通过衡量模糊工作集中聚类不确定样本与各类别子聚类结果的关系,进一步对其进行正确划分,得到更符合人类认知的非平衡数据聚类结果.
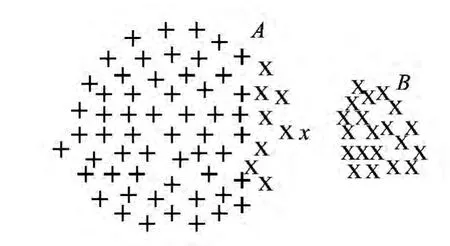
图1 非平衡分布数据聚类的均匀效应 Fig.1 The uniform effect of unbalanced data clustering
2 多中心的非平衡K-均值聚类算法
实际生活中,经常会遇到大量非平衡数据的聚类问题,传统K-均值聚类方法往往容易产生均匀效应,导致较差的非平衡聚类结果.为解决这个问题,本文提出了一种多中心的非平衡K-均值聚类算法.该方法首先对整个样本集进行聚类,并选择与聚类结果中任意两个或两个以上聚类中心距离相近的样本构成模糊工作集;然后对各聚类结果进行二次聚类,得到聚类结果中各类的子类集合,同时根据工作集中样本与每个类中最近子类中心的距离关系,对模糊工作集中的样本进行二次归类,有效避免了传统K-均值聚类方法处理非平衡数据聚类时产生的均匀效应问题.
多中心的非平衡K-均值聚类方法示意图如图2所示.图中,从人的认知的角度讲,该训练集应该聚为A区域样本和B区域样本两类,且A区域中的样本x应该属于A类,但由于A区域较大,其边界样本x与A类中心的距离要大于与B类中心的距离,因此传统K-均值聚类方法错误地将样本x划分到B类,产生了非平衡数据聚类的均匀效应.而本文提出的MC_IK方法在传统K-均值聚类基础上,选择边界附近类似样本x这种类别最不确定的样本构成模糊工作集,并对聚类结果中的每类数据分别进行二次聚类,此时,如果A类样本中存在一个子类中心cA,使得样本x与A类中最相似的子类类心cA的距离就有可能小于B类中最相似的子类类心cB的距离,此时就将样本的归属由B类校正成为A类.
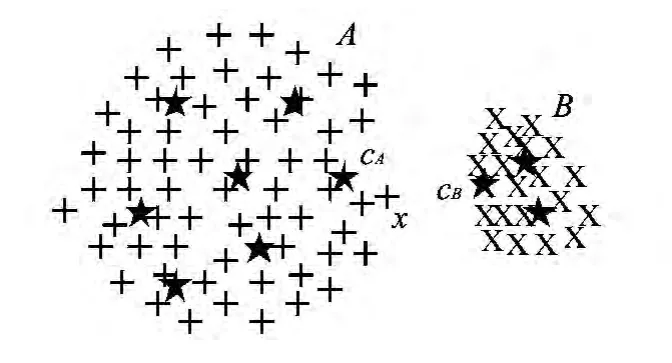
图2 多中心的非平衡K-均值聚类 Fig.2 Imbalanced K-means clustering with multiple centers
具体地,多中心的非平衡K-均值聚类算法执行过程如下.
初始化:假设样本集合为X={xi}ni=1,初始聚类参数为k(0),多中心化子类参数为k,工作集选择参数为δ.
Step 1:对样本集X进行初始标准K-均值聚类,得到初始聚类划分结果
Step 2:构造模糊工作集.对于任意一个样本xi,如果存在至少两个类Xs与Xt,且它们的类心cs和ct与该样本的距离符合如下关系:
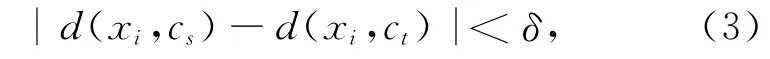
则将样本xi归入工作集;
Step 3:构造多中心类别.对Step 1得到的聚类结果中的每个类Xj并行执行Step 1的聚类方法(聚类参数为多中心化子类参数k)聚为k个子类,即得到二次聚类结果
Step 4:对模糊工作集中的每个样本xi,重新判断其与每个子类X2jp(j=1,…,k0;p=1,…,k)的类中心距离,并将样本xi归入距离最小的中心所属类别Xj中;
3 实验结果及分析
本文与传统K-均值聚类方法进行了对比.实验构造了非平衡正态分布的聚类数据集,三个分布中心依次分别为(2,2),(2,-2),(0,0),协方差矩阵依次分别为和且每类数据集的规模均为100,共300个,数据集分布如图3所示.初始聚类参数直接设置为3,多中心化子类参数设置为5.图中椭圆区域内的样本为需要关注的边界样本.
首先采用传统聚类方法进行聚类,聚类个数参数取3,得到的聚类结果如图4所示.从图中可以看出,采用传统聚类方法时,分布在较大正态分布区域的样本由于均匀效应被聚为了其他类别,如图中椭圆区域内的多数样本在构造数据集时是属于A类,而采用传统K-均值聚类方法使得大多数数据集都聚为了B和C类,即发生了聚类的均匀效应.
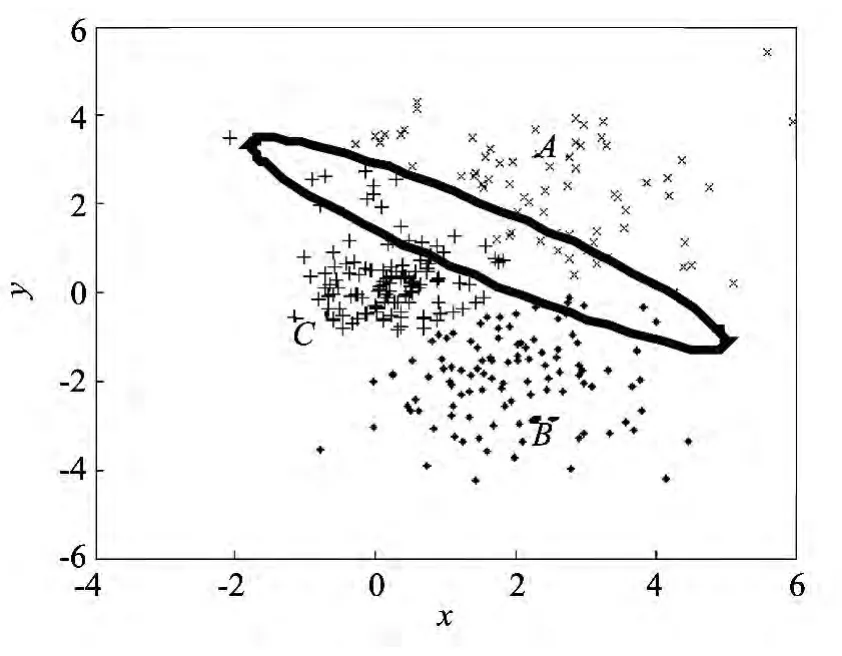
图4 传统聚类方法得到的聚类结果 Fig.4 Clustering results of traditional clustering method
采用本文提出的多中心非平衡K-均值聚类方法得到的聚类结果如图5所示.可以看出,由于通过构建模糊工作集,并对模糊工作集中的样本进行了结合二次聚类进行了重新划分,使得原本与A类聚类中心距离较大的样本,通过衡量其与A类二次聚类后得到的子类中心距离,将其归入距离较小的A类样本的子类,最终正确归入A类,有效避免了非平衡分布数据聚类问题中的均匀效应.
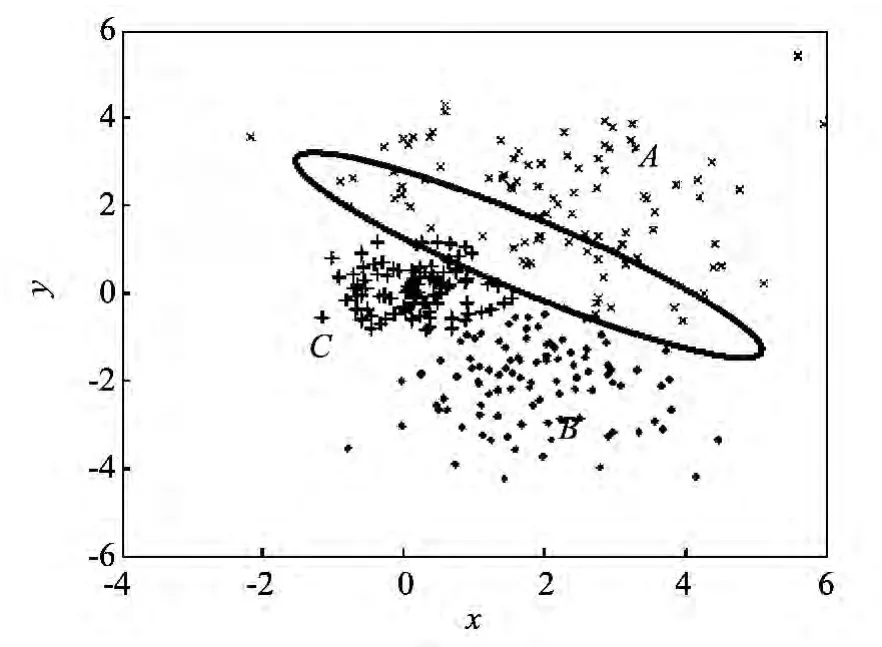
图5 MC_IK方法聚类结果图 Fig.5 Clustering result figure of MC_IK method
综上可看出,本文提出的多中心的非平衡K-均值聚类方法通过提取聚类边界样本构建模糊工作集,然后对聚类结果进行二次聚类,即得到每个类的子类,通过比较模糊工作集中样本与各类别子类中心的距离,以对模糊工作集中的样本进行正确分类,使聚类结果受样本不均衡分布的影响减弱,减小了非平衡聚类的均匀效应,能有效处理非平衡数据聚类问题.
4 结束语
针对传统K-均值聚类方法解决非平衡分布数据聚类任务时产生均匀效应的问题,本文提出一种多中心的非平衡K-均值聚类方法,消减非平衡数据聚类的均匀效应.该方法首先对整个样本集进行聚类,产生初始聚类结果,并选择与初始聚类结果中任意两个或两个以上聚类中心距离同时较近的类别模糊样本构成模糊工作集,然后对聚类结果中各类别分别进行二次聚类,得到二次聚类的子聚类结果,即获得各类的子类集合,同时根据模糊工作集中的样本与各子类中心的相似性,对工作集中的样本进行二次归类,从而消减模糊工作集中样本聚类的错误,有效避免了非平衡聚类的均匀效应.在未来的工作中,将进一步结合其他非平衡数据处理方法,提高MC_IK方法处理非平衡聚类问题的性能,并将其应用到网络入侵检测、疾病检验等实际非平衡聚类应用问题当中.
[1]钟晓,马少平,张钹,等.数据挖掘综述[J].模式识别与人工智能,2001,14(1):48-55.Zhong Xiao,Ma Shaoping,Zhang Bo,et al.Summary of data mining[J].Pattern Recognition and Artificial Intelligence,2001,14(1):48-55.(in Chinese)
[2]Deufemia V,Risi M,Tortora G.Sketached symbol recognition using latent-dynamic conditional random fields and distance-based clustering[J].Pattern Recognition,2014,47(3):1159-1171.
[3]Portela N M,Cavalcanti G,Ren T I.Semi-supervised clustering for MR brain image segmentation[J].Expert Systems with Applications,2014,41(4):1492-1497.
[4]Voevodski K,Balcan M F,Roglin H,et al.Active clustering of biological sequences[J].Journal of Machine Learning Research,2012,13,203-225.
[5]张敏,于剑.基于划分的模糊聚类算法[J].软件学报,2004,15(6):858-868.Zhang Min,Yu Jian.Fuzzy partitional clustering algorithms[J].Journal of Software,2004,15(6):858-868.(in Chinese)
[6]Rudi L.A fast quartet tree heuristic for hierarchical clustering[J].Pattern Recognition,2011,44(3):662-677.
[7]陈昊,侯慧群,杨承志,等.SA-BFSN:一种自适应基于密度聚类的算法[J].计算机工程与应用,2012,48(36):186-189.Chen Hao,Hou Huiqun,Yang Chengzhi,et al.SABFSN:adaptive algorithm based on density clustering[J].Computer Engineering and Applications,2012,48(36):186-189.(in Chinese)
[8]Su M C,Chou C H.A modified version of the k-means algorithm with distance based on cluster symmetry[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(6):674-680.
[9]许华杰,李国徽,杨兵,等.基于密度的不确定性数据概率聚类[J].计算机科学,2009,36(5):68-71.Xu Huajie,Li Guohui,Yang Bing,et al.Probabilistic density-based clustering of uncertain data[J].Computer Science,2009,36(5):68-71.(in Chinese)
[10]王玲,薄列峰,焦李成.密度敏感的半监督谱聚类[J].软件学报,2007,18(10):2412-2422.Wang Ling,Bo Liefeng,Jiao Licheng.Density-sensitive semi-supervised spectral clustering[J].Journal of Software,2007,18(10):2412-2422.(in Chinese)
[11]Celebi M E,Kingravi H A,Vela P A.A comparative study of efficient initialization methods for the kmeans clustering algorithm[J].Expert Systems with Applications,2013,40(1):200-210.
[12]Elkan C.Using the triangle inequality to accelerate kmeans[C].Proceedings of the Twentieth International Conference on Machine Learning(ICML2003),Menlo Park,AAAI Press,2003:147-153.
[13]刘广聪,黄婷婷,陈海南.改进的二分K均值聚类算法[J].计算机应用与软件,2015,32(2):261-263,277.Liu Guangcong,Huang Tingting,Chen Hainan.Improved bisecting k-means clustering algorithm[J].Computer Applications and Software,2015,32(2):261-263,277.(in Chinese)
[14]Vinnikov A,Shai Shalev-Shwartz.K-means recovers ICA filters when independent components are sparse[C].Proceedings of the 31st International Conference on Machine Learning.Beijing,China,2014:712-720.
[15]陈思,郭躬德,陈黎飞.基于聚类融合的不平衡数据分类方法[J].模式识别与人工智能,2010(6):772-780.Chen Si,Guo Gongde,Chen Lifei.Clustering ensembles based classification method for imbalanced data sets[J].Pattern Recognition and Artificial Intelligence,2010(6):772-780.(in Chinese)
[16]Yen S J,Lee Y S.Cluster-based under-sampling approaches for imbalanced data distributions[J].Expert Systems with Applications,2009,36(3):5718-5727.
[17]Ester M,Kriegel H P,Sander J,et al.A densitybased algorithm for discovering clusters in large spatial datasets with noise[C].Proceedings of the 2nd International Conference on ACM Special Interest Group Knowledge Discovery Data Mining,1996:226-231.
[18]Jing L P,Ng M K,Huang Z X.An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data[J].IEEE Transactions on Knowledge Data Engineering,2007,19(8):1026-1041.
[19]Zhang J S,Leung Y W.Robust clustering by pruning outliers[J].IEEE Transactions on Systems,Man and Cybernetics B,2003,33(6):983-998.

