一类增长网络模型的生成树

张婉佳，刘 霞，姚 兵

（西北师范大学数学与统计学院，甘肃 兰州730070）

物联网是一个基于互联网、传统电信网等信息承载体，让所有能够被独立寻址的普通物理对象实现互联互通的网络.众所周知，图论的方法已经成功地应用到各种网络研究中［1－8］.由于我们周围的网络几乎都是无标度网络 （scale－free networks）和小世界网络（small－world networks）［9－10］，这些大型动态网络有着庞大的节点和连线，无法用图形将他们描绘和刻画.然而，一般网络均是连通的.图论中研究连通性的有力工具之一是生成树.而且生成树已经成功地应用到实际问题研究［11］，积累了大量的理论成果.生成树最典型的应用之一是Perlman Radia［12］利用生成树与网络间的结构关系发明了广泛用于网桥、交换机上的生成树协议.毫无疑问，物联网的研究必将给数学本体带来新问题、新课题，从而产生新的研究对象，研究结果的积累和升华最终将导致新数学分支的产生［1］.

为了更好地理解和认识复杂网络，人们采用建立动态网络模型来逼近或模拟现实网络［13－14］，刻画其拓扑结构.张忠志等［13］通过迭代算法给出一类增长网络模型，刻画了其拓扑性质，但没有涉及生成树，而且他们的增长网络模型初始状态是一个三角形.一般地，增长网络的初始状态是任意的.基于文献［13］的增长网络模型，本文建立了初始网络可以是任何一个连通网络的增长网络模型，并给出其基本性质和具有最多叶子生成树，提出一些新的统计方法，文中涉及的图均为简单、无向、有限图.记号［m，n］代表集合｛m，m＋1，…，n｝，整数m和n满足0≤m＜n.度数为1的节点叫做叶子.若一个节点u连有k条边，则称u为k－度节点.（p，q）－图是有p个节点和q条边的图.

1 基本概念和边界增长网络模型

令 N（0）是有nv（0）个节点和ne（0）条边的连通初始网络（以下初始网络总是连通的，不再特别指出），V（0）和E（0）分别为 N（0）的节点集合和边集合.显然，nv（0）＝｜V（0）｜，ne（0）＝｜E（0）｜.对于 N（0）中的每条边uv，增加一个不在N（0）中的新节点w，并且将w与边uv的两个端点u和v分别连接，得到一个新网络模型N（1）.网络模型N（1）的节点集合为V（1）＝V（0）∪X1，边集合为E（1）＝E（0）∪Y1，其中X1是新加入到初始网络N（0）的节点之集，Y1＝｛wu，wv：uv∈E（0），w∈X1｝是新添加进初始网络N（0）的边之集.网络模型N（1）有如下的性质：节点数目nv（1）＝nv（0）＋ne（0），边数目ne（1）＝ne（0）＋2ne（0）＝3ne（0），其中ne（0）＝｜X1｜，2ne（0）＝｜Y1｜.注意到，｜Y1｜＝2｜X1｜.对于整数t≥2，在第t步，对第t－1步中产生的网络模型N（t－1）中的新增边集合Yt－1的每条边添加一个新节点w，并且将w与这条边的两个端点分别连接，从而得到高阶的网络模型N（t），以下称作边界增长网络模型.图1的例子解释边界增长网络模型N（t）.模型N（t）的节点集合和边集合分别为：

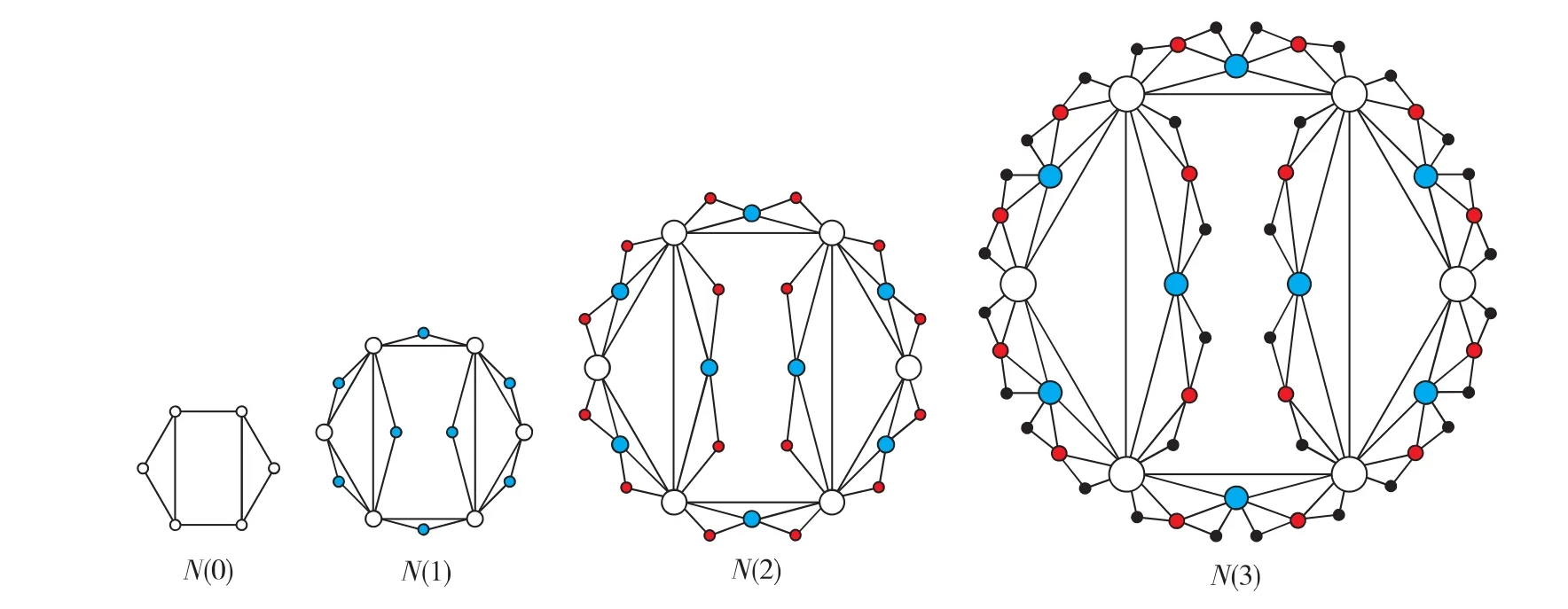
图1 增长网络模型N（k），k＝0，1，2，3Fig.1 Four network models N（k），k＝0，1，2，3

其中，Xt是新加入到N（t－1）的节点的集合，新添加的边的集合Yt＝｛wu，wv：uv∈Yt－1，w∈Xt｝.注意到：｜Xt｜＝｜Yt－1｜，｜Yt｜＝2｜Xt｜，这里Y0＝E（0），｜Xt｜＝ne（0）×2t－1.令nv（t）和ne（t）分别表示边界增长网络模型N（t）的节点数目和边数目.根据公式（1），有

边界增长网络模型N（t）的平均度〈k〉满足

故，N（t）属于稀疏型模型.令Δ（N（0））是 N（0）的最大度.边界增长网络模型N（t）的最大度Δ（N（t））＝（t＋1）·Δ（N（0）），最小度δ（N（t））＝2.

2 具有最多叶子的生成树

不失一般性，边界增长网络模型N（t）的具有最多叶子的生成树总记为TM（t）.用L（H）表示一棵树H的全体叶子的集合，则对N（t）的每一棵生成树H，都有｜L（TM（t））｜≥｜L（H）｜.下面，我们将证明高阶边界增长网络模型N（t）的一棵生成树TM（t）可以从低阶边界增长网络模型N（t－1）的一棵生成树TM（t－1）通过添加叶子而获得.由于N（t）的直径不大于TM（t）的直径，我们将要用TM（t）的直径来说明N（t）是小世界网络模型.记N（t）的节点u的度数为d（N（t），u）.

2.1 具有最多叶子生成树的性质

引理1 对于所给定的初始网络N（0）和整数t≥1，边界增长网络模型N（t）的任何生成树TM（t）满足Xt⊂L（TM（t））.

证明 考虑 X1⊂L（TM（1））.假设在 N（1）中存在一个节点w∈X1，但是它不属于叶子集合L（TM（1））.由于在N（1）中节点w为2－度节点，并且和N（1）中的边界边uv∈E（0）的2个端点相邻.所以u和v中至少有一个不是TM（1）的叶子，不妨设u∉L（TM（1））.通过删除边wv，连接u和v，则有N（1）的另一棵生成树H.显然，w∈L（H），L（TM（1））⊂L（H），从而有｜L（H）｜＞｜L（TM（1））｜，这与 TM（1）具有最多叶子的定义冲突.对t≥2，同理可证 Xt⊂L（TM（t））.

引理2 设初始网络N（0）的每一个节点的度数至少是2.则对t≥2和0≤k≤t－2，边界增长网络模型 N（t）的生成树TM（t）的叶子集L（TM（t））和边界增长网络模型N（k）的节点集V（k）没有公共节点，即是L（TM（t））∩V（k）＝ø.

证明 对t＝2，假设有节点v∈L（TM（2））∩V（0）.由于初始网络N（0）的每一个节点的度数至少是2，所以节点v在N（1）中与节点u和u′分别相邻.在N（2）中，关于节点v及其周围的结构如图2（a）所示.因为节点v是生成树TM（2）的叶子，则与节点v相邻的节点w1和w2都不是TM（2）的叶子，与节点v相邻的节点w1，2和 w2，1必须是 TM（2）的叶子（见图2（b））.则可构造边界增长网络模型N（2）的另一棵生成树H如下：在生成树TM（2）中，用边将节点v与节点w1，2和 w2，1分别连接，删去边 w1w1，2和边 w2w2，1.显然，N（2）的生成树H 的叶子数目比TM（2）的叶子数目多1（见图2（c）），这矛盾于生成树TM（2）是N（2）的叶子数目最多的生成树的定义，故有L（TM（2））∩V（0）＝ø.

图2 引理2证明的图示Fig.2 Adiagram for illustrating the proof of Lemma 2

当t≥3时，若有节点a∈L（TM（t））∩V（k），则节点a在边界增长网络模型N（k）中的度数至少是2，采用完全相同于上面的证明方法，我们仍可得到矛盾.换句话说，L（TM（t））∩V（k）＝ø.本引理得证.

令D（H）是网络 H 的直径，即D（H）＝max｛d（x，y）：x，y∈V（H）｝，这里的d（x，y）是节点x 与节点y间最短路的边数目.

定理1 设初始网络N（0）有ne（0）条边，则当t≥3时，边界增长网络模型N（t）的任何一棵生成树TM（t）的叶子个数为

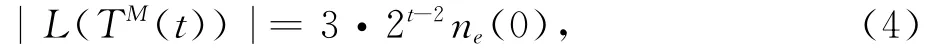
它的直径满足 D（TM（t））≤D（TM（0））＋2（t－1）.

证明 定义边界增长网络模型N（t）的节点的标号函数f 为：f（u）＝0，u∈V（0）；f（u）＝j，u∈Xj，j∈ ［1，t］.由引理1，知 X1∩L（TM（1））＝X1.所以，（L（TM（1））＼X1）⊆L（TM（0））.令l（0）＝｜L（TM（0））｜－｜L（TM（1））＼X1｜，则生成树 TM（1）的叶子数目为｜L（TM（1））｜＝｜X1｜＋l（0）.当t≥3时，根据边界增长网络模型 N（t）的构造和引理 2，TM（t）可由TM（t－1）生成.由TM（1）生成TM（2）的方法如下：对节点 u ∈V（TM（1））且 f（u）＝0，给 u 添加d（N（0），u）片叶子，得生成树 TM（2）的叶子数目｜L（TM（2））｜＝ ｜ X1｜＋ ∑u∈V（0）d（N（0），u）＝3ne（0）.同理，TM（3）可由TM（2）经如下的方法生成：给满足f（u）＝0的节点u添加d（N（0），u）片叶子，给满足f（v）＝1的节点v添加2片叶子，则得｜L（TM（3））｜＝｜X2｜＋2｜X1｜＋∑u∈V（0）d（N（0），u）＝6ne（0）.一般地，边界增长网络模型N（t）的构造说明生成树TM（t）可给生成树TM（t－1）添加叶子得来，即给TM（t－1）中满足f（u）＝0的节点u添加d（N（0），u）片叶子，给 TM（t－1）中满足t－2≥f（v）≥1的节点v添加2片叶子.从而，TM（t）的叶子个数为

公式（4）得证.根据TM（t）的构造，每次给生成树TM（t－1）添加叶子得到生成树TM（t），也就是说，给生成树TM（t－1）的最长路增加了2.注意到，TM（1）和TM（2）的直径均不超过 D（TM（0））＋2.则当t≥3 时，TM（t）的 直 径 满 足 D（TM（t））≤D（TM（0））＋2（t－1）.本定理得证.

当t→∞，定理1的结论导致下面的2个极限

以及

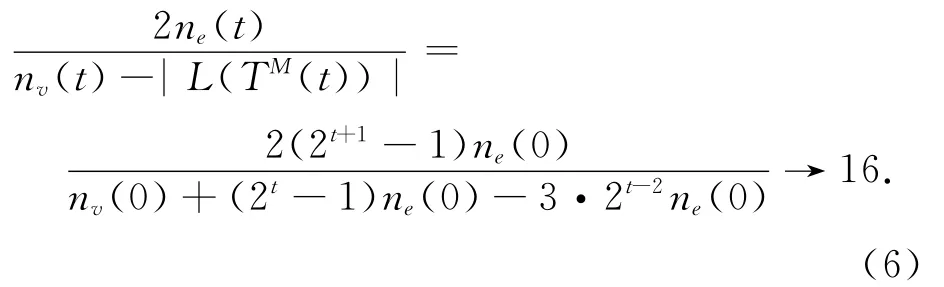
由式（5）可以看到，生成树TM（t）的每个非叶子节点平均控制3片叶子；式（6）说明TM（t）中每个非叶子节点平均控制边界增长网络模型N（t）的16条边.

2.2 具有最多叶子生成树的统计指标

2.2.1 度 谱

下面的讨论总假定初始网络N（0）的每一个节点的度数至少是2.根据引理2的结论及其证明，当t≥2时，则生成树TM（t）的度谱为（图3）：

（i）在 TM（t）中，Xt，Xt－1的节点均为 TM（t）的叶子；

（ii）在TM（t）中，Xi－1的节点的度均为2（t－i）＋1，i∈［2，t－1］；

（iii）在 TM（t）中，V（0）的节点u 的度为 （t－1）d（N（0），u）＋d（TM（1），u）.

也就是说，TM（t）＼V（0）中度数d＝1，3，5，2（t－2）＋1的节点个数nt（d）＝｜Xt｜＋｜Xt－1｜，｜Xt－2｜，｜Xt－3｜，…，｜X1｜.

设n0（di）是初始网络N（0）中度数为di的节点的个数，且di≥di＋1，i＝1，2，…，p－1.不难算出，在初始网络N（0）中度数为di的节点i在N（t）中的度数为dti.从而，生成树TM（t）的度谱为：度数d＝1，2，4，6，…，2（t－2），2（t－1）＋1，2t，2t＋2，dtp，dtp－1，…，dt1的节点个数nt（d）＝｜Xt｜，｜Xt－1｜，｜Xt－2｜，｜Xt－3｜，…，｜X1｜，n0（dp），n0（dp－1），…，n0（d1）.

2.2.2 度分布

由于TM（t）的度谱是离散型，则可计算它的随机选择恰好有k条边的节点的概率P（k）.对τ＜t和k＝2（t－τ＋1）＋1，有

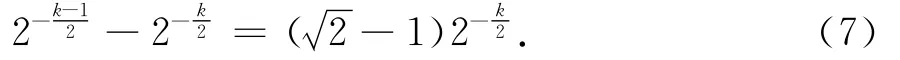
上式说明，最多叶子生成树TM（t）服从指数分布，TM（t）亦为指数型生成树.

2.2.3 边累积分布

在k （＜t）时 刻，TM（k）的 边 数 目 记 为｜E（TM（k））｜，则对τ＜t，TM（t）的边累积分布为

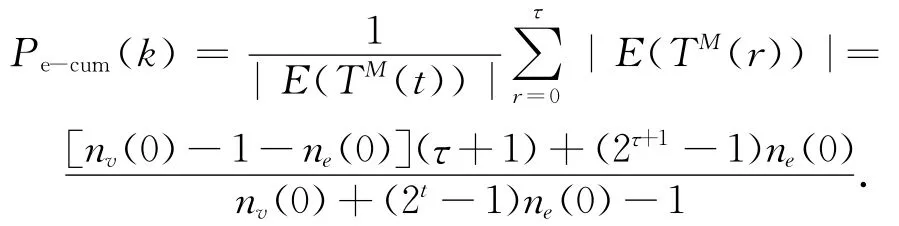
上式导致 Pe－cum（k）∝2τ＋1－t.取τ＝ （t－1）－.这就证得最多叶子生成树TM（t）的边累积分布Pe－cum（k）服从幂律分布k－γk，其中γk＝2＋

2.3 （αk，βk）－生成树

计算TM（t）中度数不大于k的节点总数ST（≤k）＝∑d≤knt（d），以及度数不大于k的节点的度数总和DT（≤k）＝ ∑d≤kd·nt（d），则TM（t）中度数不小于k的节点总数为ST（＞k）＝nv（t）－ST（≤k）和度数不小于k的节点的度数之和为DT（＞k）＝2ne（t）－DT（≤k）.首先，计算生成树TM（t）中度数不大于k＝2（t－τ＋1）＋1的节点总数，根据TM（t）的度谱，我们有

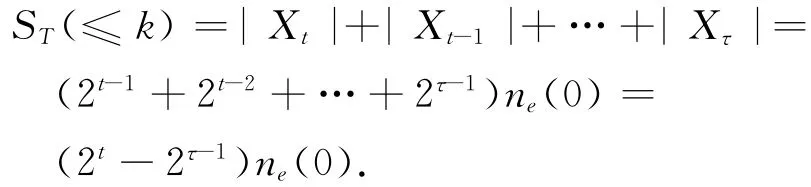
由于

图3 增长网络模型 N（k）的生成树TM（k），k＝0，1，2，3Fig.3 Four spanning trees TM（k）of the models N（k），k＝0，1，2，3

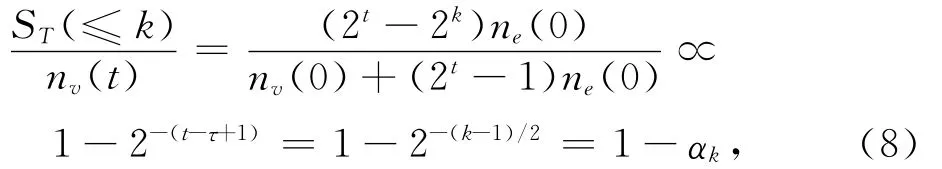
其中αk＝2－（k－1）／2.则有计算节点数目比：

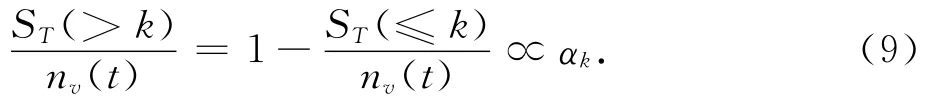
下面计算生成树TM（t）中度数不大于k的节点的度数总和

以及对较大的t，可估算

从而，当t较大时，得边数目比：

［1］Li L，Alderson D，Tanaka R，et al.Towards a theory of scale－free graphs：definition，properties，and implications［J］.Internet Mathematics，2005，2（4）：431－523.

［2］Bondy J A，Murty U S R.Graph theory［M］.London：Springer，2008：157.

［3］Yao Bing，Zhang Zhongfu，Wang Jianfang.Some results on spanning trees［J］.Acta Mathematicae Applicatae Sinica，English Series，2010，26（4）：607－616.

［4］Yao Bing，Yao Ming，Chen Xiangen，et al.Research on edge－growing models related with scale－free small－world networks［J］.Applied Mechanics and Materials，2013，513－517：2444－2448.

［5］Yao Bing，Yao Ming，Yang Sihua，et al.Labelling edges of models from complex networks［J］.Applied Mechanics and Materials，2013，513－517：1858－1862.

［6］Wang Hongyu，Yao Bing，Yao Ming.Generalized edgemagic total labellings of models from reseaching networks［J］.Information Sciences，2014，279：460－467.

［7］Yao Bing，Yang Chao，Yao Ming，et al.Graphs as models of scale－free networks［J］.Applied Mechanics and Materials，2013，380－384：2034－2037.

［8］李振汉，唐余亮，雷鹰.基于ZigBee的无线传感器网络的自愈功能［J］.厦门大学学报：自然科学版，2012，51（5）：834－838.

［9］Barabási A L，Albert R.Emergence of scaling in random networks［J］.Science，1999，286：509－512.

［10］Watts D J，Strogatz S H.Collective dynamics of′smallworld′networks［J］.Nature，1998，393：440－442.

［11］Kim D H，Noh J D，Jeong H.Scale－free trees：the skeletons of complex networks［J］.Physical Review E，2004，70：1－5.

［12］Perlman R.Hierarchical networks and the subnetwork partition problem［J］.Computer Networks and ISDN Systems，1985，9：297－303.

［13］Zhang Zhongzhi，Rong Lili，Guo Chonghui.A deterministic small－world network created by edge iterations［J］.Physica A，2006，363：567－572.

［14］杨光松，陈朝阳，袁飞.水声无线传感网中延迟敏感应用的跨层方案［J］.厦门大学学报：自然科学版，2014，53（3）：336－341.