最小二乘有限元法求解非定常应力的Navier⁃Stokes方程

孙晨扬，李启良，杨志刚（同济大学上海地面交通工具风洞中心，上海 201804）

文章编号：1001⁃246X（2015）01⁃0013⁃07

最小二乘有限元法求解非定常应力的Navier⁃Stokes方程

孙晨扬，李启良，杨志刚
（同济大学上海地面交通工具风洞中心，上海 201804）

为精确求解非定常层流问题，发展一种非定常速度－应力－压力的方法.采用牛顿法对非线性对流项进行线性化处理和预处理共轭梯度法，实现了非定常应力形式Navier⁃Stokes方程的求解.方腔层流流动比较发现，非定常应力形式比涡量形式与试验结果更加吻合，精度更高.该方法有效地解决亚格子应力项的问题，实现基于最小二乘有限元法的湍流求解.比较方腔湍流流动的试验与仿真结果，证明本文的方法具有可行性，为湍流大涡模拟计算打下基础.

最小二乘有限元法；非定常速度－应力－压力；大涡模拟；方腔流

0 引言

流体流动均为非定常流动，包括层流和湍流.为有效模拟流体流动，常用的有限差分法和有限体积法均发展了相应的非定常形式［1－3］.最小二乘有限元法作为与之相对应的方法，已发展了非定常的速度－涡量－压力形式，并在层流流动中有所应用［4］.

近年来基于有限体积法的大涡模拟在工程和研究中得到广泛应用.然而，这些计算结果均与试验结果差距较大［5－6］.主要原因是有限体积法的精度限制在二阶.而最小二乘有限元法具有通用性强、计算效率高、收敛性好和计算准确并且能够使用高阶精度等特点［4］，成为获得精确湍流结果的新方法.

由于传统的速度－涡量－压力形式无法处理大涡模拟出现的亚格子应力项，本文首先发展非定常的速度－应力－压力形式，在此基础上，引入亚格子应力，并由此发展可以求解湍流的方法.通过方腔流动的数值计算与试验对比，评估本文方法的准确性，为最小二乘有限元方法在湍流计算中的应用提供支撑.

1 数值方法

1.1 非定常应力形式的N⁃S方程

非定常不可压无量纲应力形式的N⁃S方程，

式中，u为速度，p为压力，Sij为应力张量，f为体积力，Re代表雷诺数.二维问题有6个未知量，三维问题有10个未知量.

1.2 大涡模拟控制方程及亚格子应力模型

按照大涡模拟理论［7－8］，经滤波函数处理后的不可压缩大涡模拟控制方程为

为求解大涡模拟控制方程，引入亚格子应力模型，即给出体现小尺度涡对求解方程影响的亚格子应力项ij的表达式.本文采用Smagorinsky亚格子模型

式中，νt是亚格子尺度的湍动粘度，Δi代表沿i轴方向的网格尺寸，Cs称为Smagorinsky常数，暂取0.1.

1.3 时间离散形式

时间离散方式对计算流体力学的精度和收敛性有较大影响［7－8］.综合考虑精度和效率，采用经典的θ方法.时间离散后如

式中，上标n＋1代表当前时间步的物理量，n代表上一时间步的物理量，Δt代表时间步长，θ是时间离散方式的参数.

参数θ的取值通常有两种方法：θ＝1对应于全隐式时间方案，具有一阶的时间精度，既可用于时间推进的计算，也可用于获得稳态流动结果；θ＝0.5对应于Crank⁃Nicolson方案，该方案具有二阶的时间精度，常用于计算非定常流动情况，本文采用Crank⁃Nicolson方案进行时间离散.

1.4 最小二乘有限元解法

文献［9］给出定常应力形式层流的最小二乘有限元解法的基本步骤，在此不一一列举.本文的最大差别主要体现在时间项和亚格子应力项的处理上，具体表现为刚度矩阵各系数的不同，如式（5）所示.

结合文献［9］中理论，使用C＋＋语言编写计算程序，便可以开展基于最小二乘有限元法的流体计算.计算程序的关键在于亚格子湍动粘度的计算和迭代求解算法的编写.计算效率由系数矩阵决定，最小二乘有限元法中系数矩阵为对称正定矩阵，可以采用预处理共轭梯度迭代求解，迭代收敛性很好.

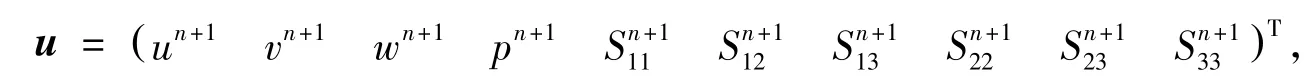
2 方腔流算例验证

方腔流动作为流体力学中经典流动，同时是对数值算法进行验证的经典问题.本文采用Prasad［10］等人的试验参数和结果.参照该试验参数建立几何模型.对于边界条件，除了顶盖给定驱动速度1m·s－1外，其它面均设为壁面.几何模型，如图1所示.由于靠近壁面处流动变化比较剧烈，且考虑到大涡模拟对近壁处的网格要求，采取两边密，中间疏的网格形式，网格数取30×30×30，近壁面第一个网格处y＋约为5，基本满足大涡模拟计算要求.划分网格如图2所示.

图1 几何模型Fig.1 Geometrymodel

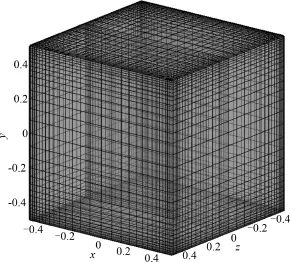
图2 网格模型Fig.2 Meshmodel

根据Prasad等人的试验结果，对图1中正方形对称面的两条中线上的速度按时间记录，并最终比较它们的平均值与均方根值跟试验之间的误差，下文比较图中，点表示试验结果，线表示计算结果.

2.1 Re＝3 200

雷诺数Re＝3 200时，流动属于层流［10］.设定时间步长为0.1 s，每个时间步长内迭代10次，使之达到收敛.整个仿真计算了4 000个时间步长，取后2 000个时间步长用于数据统计.涡量和应力形式的平均值与试验结果的比较，如图3所示.

从平均速度比较结果可以看出应力形式的结果比涡量形式的结果与试验值更加接近，具有更高的精确性.具体表现为，应力形式的速度平均值与试验值的变化趋势相同，并且在数值上也十分接近.除个别点（x/B＝－0.1处，v试验＝0.017，v仿真＝0.029和y/D＝0.1处，u试验＝－0.018，u仿真＝－0.008）外，在－0.45≤x/B≤0.45（B为方腔的宽度）和－0.45≤y/D（D为方腔的深度）≤0.45内，试验与仿真的误差都在15%以下；在靠近壁面附近，速度梯度较大的区域，应力形式的仿真结果也能与试验结果保持一致．而涡量形式的仿真结果在0.3≤｜x/B｜≤0.5（B为方腔的宽度）和0.3≤｜y/D｜（D为方腔的深度）≤0.5均有不同程度的偏差，个别点的偏差超过100%.

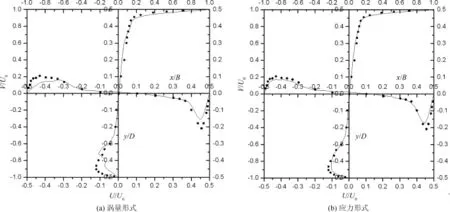
图3 无量纲速度平均值Fig.3 Non⁃dimensionalmean velocity，（a）vorticity formulation，（b）stress formulation

图4所示为无量纲速度均方根的试验值与应力形式代码计算结果的比较.同样能够发现其与试验结果吻合的较好，仿真结果与试验结果的变化趋势相同，在数值上也比较接近，误差在大部分点都在30%以下，对于无量纲速度均方根来说，这一结果是可以接受的.涡量形式得到的无量纲速度均方根在所有测点均小于0.01，与试验结果差距较大.顶盖驱动的方腔流动是由顶盖以剪切力的形式带动整个方腔流体流动.它是典型的剪切力驱动的流动.正因如此，与涡量形式相比，应力形式由于能够在边界和整个计算区域直接给出或计算出剪切应力，因而具有更高精度.涡量形式则需要获得速度梯度后才能计算出剪切应力，受网格的影响，必然会有相应的数值误差.这些误差在速度梯度较大的地方更为明显，从而导致在上述速度变化剧烈的地方，与试验差距较大.

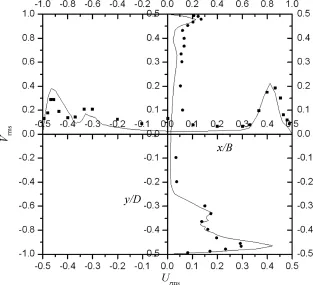
图4 无量纲速度均方根（Urms＝10 U－′2/U0，Vrms＝10 V－′2/U0）Fig.4 Non⁃dimensional root⁃mean square velocity

2.2 Re＝10 000

当雷诺数Re增大到10 000时，此时方腔流动进入到湍流状态［10］.湍流耗散起着重要的作用.为了有效模拟方腔的湍流流动，本文发展了基于最小二乘有限元的大涡模拟方法.应该指出的是，整个计算设置均与上述设置相同.图5和图6分别给出了无量纲速度平均值和均方根值.

从图中可以看出，雷诺数增大改变了无量纲速度平均值的变化规律.首先它使靠近壁面的区域速度变化更加陡峭，更加符合湍流边界层内速度分布规律.另外，对于x/B处，它的最大值有所减少，最小值有所增加；对于y/D，它的最小值有所增加.与层流相比，湍流粘性的作用使速度脉动更加强烈，表现出速度均方根数值更大，变化更明显.观察图6的数值曲线可以发现，基于最小二乘有限元的大涡模拟计算结果具有可信性；各测点的数值与试验值吻合较好.

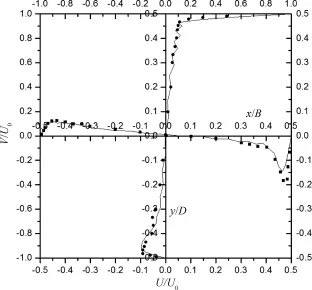
图5 无量纲速度平均值Fig.5 Non⁃dimensionalmean velocity

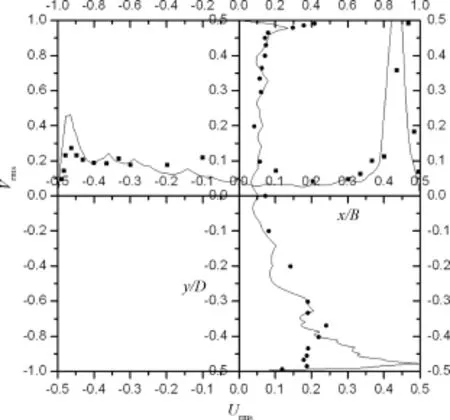
图6 无量纲速度均方根（Urms＝10 U－′2/U0，Vrms＝10 V－′2/U0）Fig.6 Non⁃dimensional root⁃mean square velocity

3 结论

发展了基于最小二乘有限元法的速度－应力－压力的非定常形式，并在此基础上引入大涡模拟方法成功实现湍流的求解.通过方腔流动的计算发现：

1）在层流流动中，传统速度－涡量－应力形式不如新发展的速度－应力－压力形式.对于顶盖驱动方腔流动，应用速度－应力－压力形式在整个监控测点区域均能获得与试验相一致的计算结果；

2）对于湍流流动，通过引入大涡模拟实现了基于最小二乘有限元法的湍流求解.对于Re＝10 000的方腔流动，本文方法成功模拟出方腔的湍流流动，取得与试验吻合较好的结果.

本文的方法能够实现非定常层流和湍流模拟.应该指出的是，本文方法有待更多算例支撑和评估，从而更加全面比较出最小二乘有限元法的优缺点.

［1］ HuangW Y，Wei JY，Ge Y B.Finite differencemethod for 3D unsteady incompressible vorticity⁃velocity formulation Navier⁃Stokes equations［J］.Journal on Numerical Methods and Computer Applications，2012，4：301－311.

［2］ An J，Sun P，Luo ZD，Huang X M.Stablized discrete finite volumemethod for unsteady Stokes equations［J］.Computational Mathematics，2011，2：213－224.

［3］ Wang F J.Analysis of computational fluid dynamics［M］.Beijing：Tsinghua University Press，2010.

［4］ Tao S.Application of the least⁃squares finite element method for computational fluid dynamics［D］.Shanghai：Tongji University，2012.

［5］ Xie Z G，Xu C X，Cui G X，Wang Z S.Large eddy simulation of flows around a square cylinder［J］.Chinese Journal of Computational Physics，2007，24（2）：171－180.

［6］ Jia X H，Liu H.Large eddy simulation of flow around two circular cylinders［J］.Chinese Journal of Hydrodynamics Edition：A，2008，6：625－632.

［7］ Gao H，Zhou X J.Implicit iteration time⁃advancement scheme for compressible Navier⁃Stokes equations［J］.Chinese Journal of Computational Physics，2008，25（1）：51－57.

［8］ Cheng J，Shu CW.High order schemes for CFD：A Review［J］.Chinese Journal of Computational Physics，2009，26（5）：633－655.

［9］ Smagorinsky J.General circulation experiments with the primitive equations：Part I.The basic experiment［J］.Monthly Weather Review，1963，91：99－164.

［10］ Ghosal S，Moin P.The basic equations for the large eddy simulation of turbulent flows in complex geometry［J］.Journal of Computational Physics，1995，118：24－37.

［11］ Tao S，Yang ZG，Gu W J，et al.Application comparison of least square finite elementmethod and finite volumemethod in CFD［J］.Computer Aided Engineering，2012，21（2）：1－6.

［12］ Prasad A K，Koseff JR.Reynolds number and end⁃wall effects on a lid⁃driven cavity flow［J］.Physics of Fluids，1989，A1：208－218.

Least⁃squares Finite Element M ethod for Unsteady Stress Formulation of Navier⁃Stokes Equations

SUN Chenyang，LIQiliang，YANG Zhigang （Shanghai AutomobileWind Tunnel Center，Tongji University，201804 Shanghai，China）

To solve unsteady laminar flow problems，a method of velocity⁃stress⁃pressure formulation instead of velocity⁃vorticity⁃pressure formulation is developed.With Newton's linearizedmethod to linearize convective terms and preconditioned conjugate gradient method to solve equations，unsteady stress formulation of Navier⁃Stokes equations is solved.Comparison between numerical and experimental results of cavity laminar flow shows that result of stress formulation fits experiment better and has higher accuracy than vorticity formulation.The stress formulation can deal with subgrid stress with least squares finite elementmethod.Comparison with experimental results of cavity turbulent flow reveals feasibility of the method.It lays a firm foundation for large eddy simulation computation.

least squares finite elementmethod；unsteady velocity⁃stress⁃pressure；large eddy simulation；cavity flow

TP301.6

A

2013－12－25；

2014－04－01

国家自然科学基金青年科学基金（11302153）；同济大学中央高校基本科研业务费专项资金（20123315）资助项目

孙晨扬（1991－），男，江苏兴化人，硕士生，主要研究车身与空气动力学，E⁃mail：sun⁃chenyang＠163.com

Received date： 2013－12－25；Revised date： 2014－04－01