粒子数密度对飞秒Gauss 型脉冲传播及光谱特性的影响

王振东，杨善迎，刘婷婷，马建玲，肖 静（.泰山学院物理与电子工程学院，山东泰安 70；.莱芜职业技术学院，山东莱芜 700）

文章编号：1001⁃246X（2015）01⁃0075⁃11

粒子数密度对飞秒Gauss 型脉冲传播及光谱特性的影响

王振东1，杨善迎2，刘婷婷1，马建玲1，肖 静1
（1.泰山学院物理与电子工程学院，山东泰安 271021；2.莱芜职业技术学院，山东莱芜 271100）

利用预估校正－时域有限差分（PC⁃FDTD）法求解全波Maxwell⁃Bloch方程，研究介质粒子数密度（N）对飞秒Gauss型激光脉冲在Λ型三能级原子介质中传播及光谱特性的影响.结果表明：小面积2π脉冲在不同N介质中都不发生分裂，脉冲频谱基本没有新的高频成分产生，随N增大中心频率附近光谱强度明显减小.面积4π脉冲，在N较大的稀疏介质及稠密介质中都产生分裂，在稀疏介质中随N增大频谱展宽幅度及高频成分强度增大，但在稠密介质中频谱展宽变小且远小于N较大时的稀疏介质情况.大面积8π脉冲，脉冲分裂情况与4π脉冲情况相似，但随N增大频谱展宽幅度及高频成分强度单调增大，且在稠密介质中的频谱展宽幅度及高频成分强度远大于N较小的稀疏介质情况.

飞秒Gauss型脉冲；粒子数密度；传播；光谱

0 引言

激光与物质的相互作用是现代物理学的一个重要研究领域，超短脉冲激光在原子或分子介质中的传播性质是目前重要的研究课题［1－13］.对长脉冲，可以采用慢变包络近似（SVEA）和旋转波近似（RWA）求解麦克斯韦－布洛赫方程（Maxwell⁃Bloch equation，M⁃B）方程，由此得出的面积定理［14－15］可以解释很多有趣的现象，如自感应透明、大面积脉冲的分裂、脉冲压缩等，但是对于少周期脉冲，这些近似不再适用［16－19］.人们已采用不考虑SVEA和RWA的全波M⁃B方程对超短脉冲在二能级介质中的传播问题进行了广泛的研究［1－2，16－22］，如Ziolkowski等人发现载波场的时间导数项对二能级系统的演化有重要的影响［16］，Hughes发现大面积（＞10π）超短脉冲发生载波拉比振荡（CWRF），从而导致载波整形和光谱中高频成分的产生［17］，这一结论被以后的实验证实［18］，肖健等研究发现，与长脉冲不同，周期量级超短脉冲不是通过脉冲分裂而是通过脉冲压缩进行面积演化［22］.最近，周期量级超短脉冲在三能级及多能级系统中的传播和激发问题引起人们的极大兴趣［12－13，23－26］，如谭霞等研究了相对载波包络相位对双色超短脉冲激光在V型三能级原子系统中传播特性的影响［12］，陆剑清等分析了超短激光脉冲在多能级系统中的传输特性［13］，Song等讨论了周期量级激光脉冲在V型三能级系统中的传播［24］，Loiko等考察了超短脉冲在Λ型三能级系统中传播时的相干和相位灵敏现象［25］.以上研究都是关于周期量级脉冲在稀疏介质中的传播问题，在稀疏介质中只需考虑原子与超短脉冲的相互作用，而对于稠密介质，则必须考虑原子与原子之间的近偶极－偶极（NDD）相互作用，这种相互作用能导致洛伦兹局域场修正（LFC）［27－38］.最近，有些文章［4－6，27－38］在不采用SVEA和RWA的情况下讨论了NDD相互作用的影响，发现了许多有价值的现象.

对介质粒子数密度对激光脉冲的传播及光谱特性的影响，人们进行了一些探索研究.如，Ranka等［37］研究了超短脉冲在二能级系统中的相干光谱效应，发现当原子密度增加时光谱振荡增强；Kalosha等［38］讨论了超短脉冲在稠密二能级系统中传播时光学次脉冲的形成，并发现在透射光谱中产生了大的蓝移，在反射光谱中产生了大的红移；刘炳欣［39］等研究了在二能级介质中原子密度对2π超短脉冲传播的影响，发现对于较高的原子数密度，即使是2π脉冲，自感应透明也不再发生，但是对于更大面积的脉冲并没有进一步展开讨论.本文选择更具有实用价值的三能级系统，详细研究粒子数密度对不同面积的超短脉冲传播的影响，分析它们的光谱性质，揭示出一些新的现象.

1 系统模型和运动方程

考虑飞秒Gauss激光脉冲在由Λ型三能级原子（图1）组成的介质中传播.对Λ型三能级87Rb原子来说，能级｜3〉、｜2〉和｜1〉分别对应5S1/2（F＝1）、5S1/2（F＝2）和5P3/2（F′＝1）．下面给出的原子介质参量值都是对应于这种能级结构的87Rb原子.数值计算表明，对于粒子数密度小于N＝1.0×1026m－3的稀疏介质，NDD相互作用的影响极小，计算中不考虑NDD相互作用，对于粒子数密度大于N＝1.0×1026m－3的稠密介质，计算中需要考虑NDD相互作用的影响.

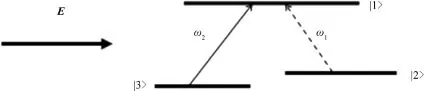
图1 Λ型三能级原子系统Fig.1 Energy levels of A⁃type atmotic system

本文讨论的是脉冲与介质在一个维度的相互作用，设脉冲光场沿z方向传播，电场Ex沿x方向极化，磁场Hy沿y方向极化．在各向同性的均匀稠密介质中，微观局域场EL、外场Ex和非线性极化强度Px之间的相关性按照Lorentz⁃Lorenz关系［40］可表示为

其中，ε0是真空介电常数.采用如下代换

u1＝ρ12＋ρ21，u2＝ρ23＋ρ32，u3＝ρ13＋ρ31，u4＝－i（ρ12－ρ21），

u5＝－i（ρ23－ρ32），u6＝－i（ρ13－ρ31），u7＝ρ22－ρ11，u8＝ρ33－ρ11，

可将系统关于ρij（i，j＝1，2，3）的复数形式的密度矩阵运动方程化为如下实数形式

此即已包含原子与原子之间的NDD相互作用导致的LFC在内的Bloch方程.其中ω1和ω2分别表示从能级｜1〉到能级｜2〉及从能级｜1〉到能级｜3〉的跃迁频率；β＝μ12/μ13为跃迁偶极矩的比值，μij是能级i和j之间的跃迁偶极矩；ΩL＝μ13EL/ħ＝Ω－ε（u3＋βu1）是对应于微观局域场EL的Rabi频率，而Ω＝μ13Ex/ħ表示与外场Ex相关的Rabi频率，ε＝/（3ε0ħ）表示NDD相互作用的强度；γm（m＝1，2，…，8）为um的驰豫速率.

Maxwell方程为

其中μ0是真空中的磁导率；Px＝－N（μ12u1＋μ13u3），N是介质的粒子数密度．

想求得Maxwell方程和Bloch方程的解析解非常困难.本文利用时域有限差分法（Finite⁃difference time⁃domain method）和预估矫正法（Predictor⁃corrector method）［16］求它们的数值解.飞秒Gauss脉冲的电场和磁场为

和

Hy（t＝0，z） ＝（ε0/μ0）1/2Ex（t＝0，z）．

其中E0为初始入射脉冲的电场强度，p是脉冲包络的半高宽度（FWHM），简称脉宽，c为真空中的光速，ωp是脉冲中心频率．入射脉冲的面积为A＝μ13E0Pπ/（2.087ħ），z0的选取是为了保证初始时刻t0＝0脉冲进入介质很少．在下面的计算中，初始条件为u7（0）＝0，u8（0）＝1，其它的um＝0（m＝1，2，…，6），即初始时刻原子都处于基态｜3〉上．脉冲和介质的参数取为ω1＝2.415 23 fs－1，ω2＝2.415 27 fs－1，ωp＝2.415 27 fs－1，p＝5 fs，β＝1，γm＝1.0×109s－1（m＝1，2，…，8），μ13＝3.584×10－29Asm，在稀疏介质中取ε＝0．

2 数值结果及分析

首先考虑小面积2π脉冲在粒子数密度较小（N＝2.0×1024m－3）和较大（N＝4.0×1025m－3）的稀疏介质以及稠密介质（N＝4.0×1026m－3）中的传播.

由图2（a）、（b）及（c）可以看出，小面积2π脉冲在传播过程中不发生分裂，但是随着粒子数密度增大，脉冲经过介质时其前沿和后沿均出现振荡，脉冲在介质中传播时的延迟现象也更加明显.另外，对比图2（d）及（e）可知，脉冲在稠密介质中传播时，脉冲的振幅减小且周期数明显增多，频率增大.因为在脉冲通过介质时，将受到群速度色散和自相位调制的共同作用，上述现象表明，随着粒子数密度的增大，脉冲在介质中传播时群速度色散和自相位调制的作用增强.

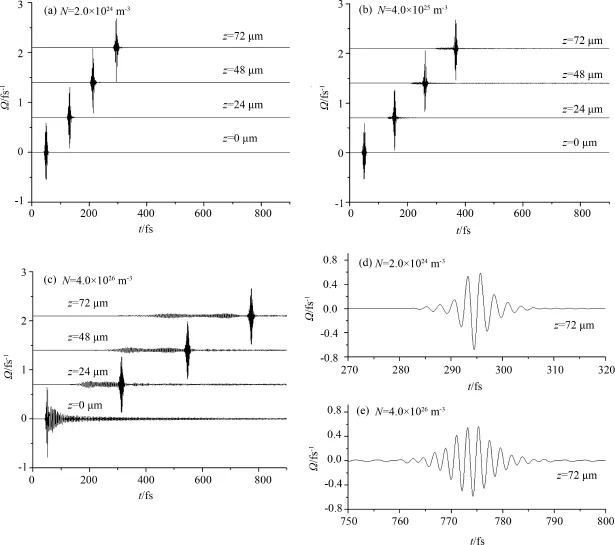
图2 （a）、（b）及（c）为2π脉冲在不同N的介质中传播到不同距离处的演化；（d）、（e）为（a）、（c）在z＝72μm处的放大图Fig.2 （a），（b）and（c）are temporal evolutions of2πpulses with different N；（d）and（e）are enlargements of（a）and（c）at z＝72μm，respectively

图3是2π脉冲分别在粒子数密度不同的介质中传播时的频谱图.由图可以看出，小面积2π脉冲在介质中传播时基本没有新的高频成分产生，但是随着粒子数密度的增大，激光脉冲与介质相互作用增强，光谱强度产生震荡.图3（c）显示在大粒子数密度的稠密介质中光谱强度分布出现了明显的红移和蓝移，中心频率附近光谱强度明显减小，红移成分和蓝移成分强度显著增大.对比图2（d）及（e）可知，这是由于在稠密介质中激光与介质的相互作用增强，脉冲的振幅减小且周期数增多，主脉冲中心频率增大出现明显的蓝移成分；而由图2（c）看出脉冲在传播过程中前沿和后沿出现较大幅度的震荡，对应图3（c）中红移成分强度增大且震荡加剧.需要说明的是，图3（c）中z＝0μm处频谱形状与（a）、（b）两图中z＝0μm处频谱形状是不同的，这与模拟运算中z0的选取是有关系的，z0的选取是为了保证初始时刻t0＝0时脉冲进入介质很少，也就是说z＝0μm处的粒子数密度并不是等于零.因此，对于稀疏介质z＝0μm处的粒子数密度较小，脉冲与介质的相互作用程度较小，初始入射脉冲能保持为完整的高斯型，但是对于高粒子数密度的稠密介质，z＝0μm处的粒子数密度较大，脉冲与介质产生相互作用程度较大，脉冲形状不再保持对称的高斯型，脉冲频谱也不再呈现对称的形状，这与后续讨论的图6（c）及图8（c）的产生原因是相同的.

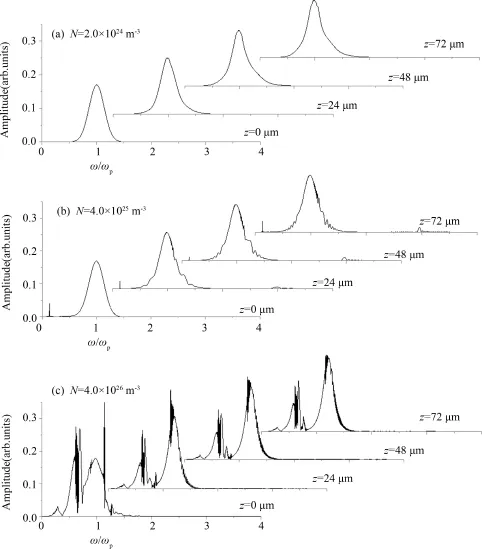
图3 2π脉冲在不同粒子数N的介质中传播的频谱Fig.3 Spectra of 2πpulses at different distances

作为对比，图4（a）、（b）是在N＝4.0×1026m－3的稠密介质中考虑及不考虑NDD效应的情况下，小面积2π脉冲传播到z＝76μm处的脉冲演化，（c）、（d）是与（a）、（b）相对应的频谱.对比图4（a）和（b）可以看出，在考虑和不考虑NDD效应时脉冲的演化出现了明显的不同，图4（b）中脉冲比图4（a）中脉冲出现了明显的延迟，且（b）图中脉冲振幅明显小于（a）图中脉冲振幅.分析产生的原因，是因为NDD效应使光与物质的相互作用增强，与不考虑NDD效应的脉冲传播情况相比，脉冲与介质相互作用后的振幅更大，在介质中的传播速度更快.再对比图4（c）与4（d）可以看出，考虑NDD效应情况下，脉冲频谱中0.5ω～0.8ω的红移成分震荡更为剧烈，这表明NDD效应对脉冲频谱中低频成分的影响更为明显.数据计算结果表明，考虑及不考虑NDD效应的情况下，2π脉冲传播到其它位置时的脉冲演化及频谱与传播到z＝76μm处的脉冲演化及频谱情况相似.

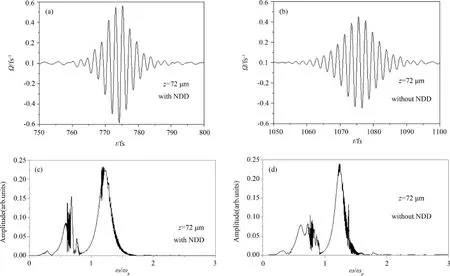
图4 2π脉冲在稠密介质中考虑NDD效应（a），及不考虑NDD效应（b）时，传播到z＝72μm处的演化；（c）、（d）分别是与（a）、（b）相对应的频谱（N＝4.0×1026m－3）Fig.4 Temporal evolutions of2πpulses in densemedium（N＝4.0×1026m－3）NDD（a）with，and（b）without NDD at z＝72μm；（c）and（d）are spectra corresponding to（a）and（b），respectively

如图5表示的是面积4π脉冲在粒子数密度不同的原子介质中的传播.由图5（a）、（b）及（c）可知，在N＝2.0×1024m－3的粒子数密度较小的稀疏介质中，脉冲不发生分裂；在N＝6.0×1025m－3的粒子数密度较大的稀疏介质中及N＝6.0×1026m－3的稠密介质中传播时脉冲都分裂为两个子脉冲，其中第一个子脉冲的振幅远大于第二个子脉冲的振幅，第一个子脉冲的周期数少于第二个子脉冲的周期数；另外，随着介质密度的增大，脉冲前沿和后沿出现震荡，特别是在N＝6.0×1026m－3的稠密介质中，因为NDD效应使激光与介质的相互作用增强，脉冲前沿及后沿出现更强烈的震荡，其第二个子脉冲的传播也产生了明显的延迟.由图5（e）及5（d），稠密介质（N＝6.0×1026m－3）中的两个子脉冲与对应的粒子数密度较大（N＝6.0×1025m－3）的稀疏介质中的两个子脉冲相比，稠密介质中的两个子脉冲的传播都出现延迟效应，且稠密介质中第二子脉冲的传播延迟效应更为明显，这是因为在稠密介质中由主脉冲分裂出的第二子脉冲的振幅比在稀疏介质中主脉冲分裂出的第二子脉冲振幅更小.进一步对比图5（f）及图5（g）可知，前一种情况中第一子脉冲为一个近似的单一周期子脉冲，后一种情况中的第一子脉冲为一个多周期子脉冲，且前一种情况中的第一子脉冲在介质中传播时的脉冲整形更为明显.

图6是4π脉冲在粒子数密度不同的介质中传播时的频谱图.由图6（a）可以看出，脉冲在N＝2.0×1024m－3的的粒子数密度较小的稀疏介质中传播时的频谱略有展宽，有新的1.5ω～2.5ω的高频成分产生，随着传播距离的增大，高频成分强度增大，这与Hughes在二能级研究的结果相符合，即由于主脉冲CWRF，导致脉冲整形，脉冲经过介质时有高频成分产生［17］.图6（b）表明，脉冲在N＝6.0×1025m－3的粒子数密度较大的稀疏介质中传播时的频谱展宽，有1.5ω～6ω高频成分产生，但图6（c）显示脉冲在N＝6.0×1026m－3的稠密介质中传播时脉冲频谱变窄，与前者相比只有1.5ω～3ω的高频成分产生.对比图5（d）、（f）及（e）、（g）可以看出，两种情况下脉冲都产生分裂，且分裂出第一个子脉冲振幅最大，其它子脉冲振幅较小，再对比2π脉冲的传播情况可知，除了第一个子脉冲外，其它子脉冲的振幅都比较小，所以在介质中传播时不能产生高频成分，因此高频成分应该主要是第一个子脉冲的CWRF导致脉冲整形产生.由前述对图5（f）与图5（g）的对比分析可以知道，前一种情况中的第一个子脉冲周期数少而脉冲整形幅度大，后一种情况中的第一个子脉冲周期数多而脉冲整形幅度小，因此第一个子脉冲周期数少而脉冲整形幅度大是产生更高频率的高频成分的主要原因.

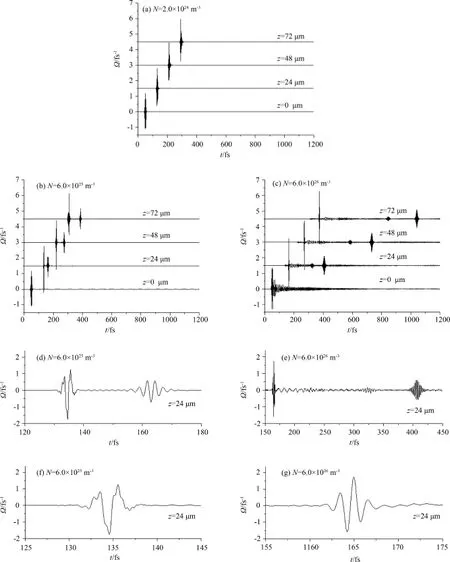
图5 （a）、（b）及（c）为4π脉冲在不同N的介质中的演化；（d）、（e）为（b）、（c）在z＝24μm处的放大图；（f）、（g）为（d）、（e）中第一个子脉冲的演化放大图Fig.5 （a），（b）and（c）are temporal evolutions of4πpulseswith different N；（d）and（e）are enlargements in （b）and（c）at z＝24μm，respectively；（f）and（g）are enlargements of the first sub⁃pulse in（d）and（e），respectively

图6 4π脉冲在不同粒子数N的介质中传播的频谱Fig.6 Spectra of4πpulseswith different N

数值计算表明，面积大于2π但小于5π的脉冲在不同粒子数密度介质中传播时，脉冲的传播及光谱性质与以上所描述的4π脉冲情况类似.

图7给出了大面积8π脉冲在粒子数密度不同的介质中的传播演化情况.由图7（a）、（b）及（c）可知，与4π脉冲在介质中传播情况相似，大面积8π脉冲在N＝2.0×1024m－3的粒子数密度较小的稀疏介质中不发生分裂，在N＝6.0×1025m－3的粒子数密度较大的稀疏介质和N＝6.0×1026m－3的稠密介质中均分裂出3个子脉冲，且分裂出的第一子脉冲的振幅大于其它子脉冲，第一子脉冲的周期数少于其它子脉冲，另外随粒子数密度增大，脉冲经过介质时其前沿及后沿的震荡更为剧烈.对比图7（d）及（e）可以看出，前一种情况中的第一子脉冲为近似1.5周期的子脉冲，后一种情况中则出现了振幅相当的两个子脉冲，其中第一子脉冲为一个近似单一周期的脉冲，第二子脉冲为一个近似1.5周期的脉冲，且两种情况下，因为子脉冲周期数少，各个子脉冲都经历了强烈的脉冲整形.

图7 （a）、（b）及（c）为8π脉冲在不同N的介质中传播的演化；（d）、（e）为图（b）、（c）中z＝48μm处时间演化放大图Fig.7 （a），（b）and（c）are temporal evolutions of 4πpulses with different N；（d）and（e）are enlargements of（b）and（c）at z＝48μm，respectively

图8是8π脉冲在粒子数密度不同的介质中传播时的频谱图.由图8（a）、（b）及（c）可以看出，大面积8π脉冲在介质中传播时随粒子数密度的增大，有更高频率的高频成分产生.其中8π脉冲在N＝2.0×1024m－3的稀疏介质中传播时脉冲没有发生分裂，有1.5ω～2.5ω的高频成分产生，与图6（a）中4π脉冲相似，高频成分是由于主脉冲CWRF导致的脉冲整形所产生；8π脉冲在N＝6.0×1025m－3介质中传播时有1.5ω ～5.5ω的高频成分产生，在N＝6.0×1026m－3介质中传播时有1.5ω～9ω的高频成分产生，由前述对图5 （f）、图7（d）与图7（e）中情况的分析可知，由于主脉冲分裂出的第一个子脉冲（图7（e）情况中还包括与第一个子脉冲振幅相当的第二个子脉冲）周期数少，脉冲经历了强烈的脉冲整形，从而导致了高频成分的产生.

数值计算表明，面积等于或大于5π的脉冲在不同粒子数密度介质中传播时，脉冲传播行为及光谱性质与8π脉冲相似.

3 结论

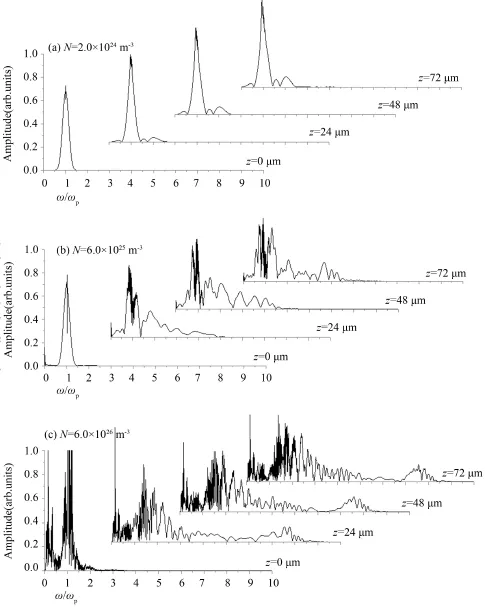
图8 8π脉冲在不同粒子数N的介质中传播的频谱Fig.8 Spectra of8πpulseswith different N

利用数值计算研究了飞秒Gauss型激光脉冲在Λ型三能级原子介质中的传播.结果表明，介质粒子数密度数值的大小对脉冲传播及光谱特性都有显著的影响，而且这个影响与脉冲面积的大小密切相关.小面积2π脉冲在粒子数密度较小和较大的稀疏介质以及粒子数密度更大的稠密介质中传播时，脉冲皆不发生分裂，脉冲经过介质时基本没有新的高频成分产生，随粒子数密度数值的增大，脉冲在介质中传播时的振幅减小，脉冲周期数增加、频率增大，脉冲光谱震荡增强，在稠密介质中光谱强度分布出现了明显的红移和蓝移，且两种成分的强度显著增大，同时中心频率附近光谱强度明显减小.面积4π脉冲，在粒子数密度较小的稀疏介质中传播时不发生分裂，脉冲频谱略有展宽，在粒子数密度较大的稀疏介质及稠密介质中传播时主脉冲都分裂为2个子脉冲，在稀疏介质中随N增大频谱展宽幅度及高频成分强度增大，但在稠密介质中频谱展宽变小且远小于N较大时的稀疏介质情况.大面积8π脉冲，脉冲分裂情况与4π脉冲情况相似，主脉冲在分裂时都分裂为三个子脉冲，但随N增大频谱展宽幅度及高频成分强度单调增大，且在稠密介质中的频谱展宽幅度及高频成分强度远大于N较小的稀疏介质情况.数值计算结果表明，面积大于2π但小于5π的脉冲的传播及光谱性质与以上所描述的4π脉冲情况类似，面积大于5π的脉冲的传播及光谱性质与以上所描述的8π脉冲情况类似.

［1］ YangW F，Song X H，LiR X，Xu Z Z.Generation of intense extreme supercontinuum radiation via resonant propagation effects ［J］.Phys Rev A，2008，78（2）：023836－1－5.

［2］ Zhang C J，Yang W F，Song X H，Xu Z Z.Phase control of higher spectral components in the presence of a static electric field ［J］.JPhy B：AtMol Opt Phys，2009，42（5）：055602－055607.

［3］ Rosanov N N，Kozlov V V，Wabnitz S.Maxwell⁃Drude⁃Bloch dissipative few⁃cycle optical solitons［J］.Phys Rev A，2010，81 （4）：043815－1－17.

［4］ Zhang C J，YangW F，Song X H，Xu Z Z.Carrier⁃envelope phase dependence of the spectra of reflected few⁃cycle laser pulses in the presence of a static electric field［J］.Phys Rev A，2009，79（4）：043823－1－6.

［5］ Zhang C J，Yang W F，Song X H，Xu Z Z.Dependence of dynamic Lorentz frequency shift on carrier⁃envelope phase and including local field effects［J］.Opt Express，2009，17（24）：21754－21761.

［6］ Xie X T，Macovei M A.Single⁃cycle gap soliton in a subwavelength structure［J］.Phys Rev Lett，2010，104（7）：073902－1－4.

［7］ Hu Q L，Liu SB，LiW.Intense Cherenkov⁃type terahertz electromagnetic radiation from ultrafast laser⁃plasma interaction［J］. Chinese Phys B，2008，17（3）：1050－1054.

［8］ Weber C，Wacker A，Knorr A.Density⁃matrix theory of the optical dynamics and transport in quantum cascade structures：The role of coherence［J］.Phys Rev B，2009，79（16）：165322－1－14.

［9］ Tan F，Peng L Y，Gong Q H.Ionization of atoms by chirped attosecond pulses［J］.Chinese Phys B，2008，18（11）：4807－4814. ［10］ HongW Y，Yang Z Y，Lan PF，Zhang Q B，LiQ G，Lu PX.Generating isolated broadband attosecond pulseswith stable pulse duration in a non⁃colinear polarized two⁃color field［J］.Acta Phys Sin，2009，58（7）：4914－4919.

［11］ Zhang SA，Zhang H，Wang Z G，Sun Z R.Selective excitation and suppression of coherent anti⁃Stokes Raman scattering by shaping femtosecond pulses［J］.Chinese Phys B，2010，19（4）：043201－1－5.

［12］ Tan X，Wang Z D，Wang L，Fan X J.Relative carrier⁃envelope phase dependence of resonant propagation of two⁃colour femtosecond pulses in V⁃type atomicmedium［J］.Chinese Phys B，2010，19（6）：064211－1－7.

［13］ Lu JQ，Zhang X Y，Zhang S A，Jia T Q，Sun Z R，Wang Z G.Propagation property of ultra⁃short laser pulses in multi⁃level quantum system［J］.Acta Phys Sin，2009，58（12）：8212－8216

［14］ McCall S L，Hahn E L.Self⁃induced transparency［J］.Phys Rev，1969，183（2）：457－485.

［15］ Lamb Jr G L.Analytical descriptions of ultrashortoptical pulse propagation in a resonantmedium［J］.Rev Mod Phys，1971，43（2）：99－124.

［16］ Ziolkowski RW，Arnold JM，Gongny DM.Ultrafastpulse interactionswith two⁃level atoms［J］.Phys Rev A，1995，52（4）：3082－3094.

［17］ Hughes S.Breakdown of the area theorem：Carrier⁃wave Rabi flopping of femtosecond optical pulses［J］.Phys Rev Lett，1998，81（16）：3363－3366.

［18］ Mücke O D，Tritschler T，Wegener M，Morgner U，Kärtner F X.Signatures of carrier⁃wave Rabi flopping in GaAs［J］.Phys Rev Lett，2001，87（5）：057401－1－5.

［19］ Song X H，Gong S Q，Li R X，Xu Z Z.Propagation of an arbitrary elliptically polarized few⁃cycle ultrashort laser pulse in resonant two⁃level quantum systems［J］.Phys Rev A，2006，74（1）：015802－1－4.

［20］ Yang W F，Song X.H，Gong SQ，Xu ZZ.Carrier⁃envelope phase dependence of few⁃cycle ultrashort laser pulse propagation in a polarmoleculemedium［J］.Phys Rev Lett，2007，99（13）：133602－1－4.

［21］ Song X H，Gong SQ，Yang W F，Xu Z Z.Propagation of an attosecond pulse in a dense two⁃levelmedium［J］.Phys Rev A，2004，70（1）：013817－1－4.

［22］ Xiao J，Wang ZY，Xu Z Z.Area evolution ofa few⁃cycle pulse laser in a two⁃level⁃atom medium［J］.Phys Rev A，2002，65 （3）：031402－1－4.

［23］ Netz R，Feurer T.Influence of phase modulation on the reshaping of ultrashort laser pulses in resonant three⁃level systems ［J］.Phys Rev A，2001，64（4）：043808－1－7.

［24］ Song X，Gong S，Xu Z.Propagation of a few⁃cycle laser pulse in a V⁃type three⁃level system［J］.Opt Spectrosc，2005，99 （4）：517－521.

［25］ Loiko Y，Serrat C.Coherent and phase⁃sensitive phenomena of ultrashort laser pulses propagating in three⁃levelΛ－type systems studied with the finite⁃difference time⁃domainmethod［J］.Phys Rev A，2006，73（6）：063809－1－11.

［26］ Wang Lei，Wang Zhendong，Liang Bian，Fan Xijun.Spatial distribution of few⁃cycle laser pulses propagating in a ladder⁃type three⁃levelmedium［J］.Chinese JComput Phys，2011，28（1）：081－086.

［27］ Tan Xia，Wang Lei，Wang Zhendong，Fan Xijun.Population of dense V⁃type three⁃levelmedium in few⁃cycle laser pulses ［J］.Chinese JComput Phys，2009，26（5）：773－780.

［28］ Wang Zhendong，Liang Bian，Liu Zhongbo，Fan Xijun.Propagation of femtosecond chirped Gaussian pulse in dense three⁃levelΛ－type atomic medium［J］.Acta Phys Sin，2010，59（10）：7038－7046.

［29］ Bowden C.M，Dowling JP.Near⁃dipole⁃dipole effects in densemedia：Generalized Maxwell⁃Bloch equations［J］.Phys Rev A，1993，47（2）：1247－1251.

［30］ Wang N J，Rabitz H.Near dipole⁃dipole effects in electromagnetically induced transparency［J］.Phys Rev A，1995，51（6）：5029－5031.

［31］ Crenshaw M.E，Sullivan K U，Bowden CM.Local field effects inmulticomponentmedia［J］.Opt Exp，1997，1（6）：152－159.

［32］ Calderón OG，Antón M A，Carreño F.Near dipole⁃dipole effects in a V⁃typemedium with vacuum induced coherence［J］.Eur Phys JD，2003，25（1）：77－87.

［33］ Dung H T，Buhmann S Y，Welsch D G.Spatial distinguishability of photons produced by spontaneous parametric down⁃conversion with a focused pump［J］.Phys Rev A，2006，74（2）：023802－1－7.

［34］ Xia K Y，Gong SQ，Liu C P.Near dipole⁃dipole effects on the propagation of few⁃cycle pulse in a dense two⁃levelmedium ［J］.Opt Exp，2005，13（16）：5913－5924.

［35］ Ma H，Fan X J，Tan X，Lu HW，Xu Z Z.Effects of Lorentz local field correction on propagation properties of few⁃cycle pulse in denseΛ－type atomic medium［J］.Opt Comm，2008，281（17）：4493－4498.

［36］ Tan X，Fan X J，Yang Y L，Tong D N.Time evolution of few⁃cycle pulse in a dense V⁃type three⁃levelmedium［J］.Journalof Modern Optics，2008，55（15）：2439－2448.

［37］ Ranka JK，Schirmer RW，Gaeta A L.Coherent spectroscopic effects in the propagation of ultrashort pulses through a two⁃level system［J］.Phys Rev A，1998，57（1）：R36－R9.

［38］ Kalosha V P，Herrmann J.Formation of optical subcycle pulses and full Maxwell⁃Bloch solitary waves by coherent propagation effects［J］.Phys Rev Lett，1999，83（3）：544－547.

［39］ Liu Bingxin，Gong Shangqing，Song Xiaohong，Jin Shiqi.Influence of atomic densities on propagation property for ultrashort pulses in a two⁃levelmedium［J］.Chinese Optics Letters，2005，3（5）：278－280.

［40］ Jackson JD.Classical electrodynamics［M］.Third ed.New York：Wiley，2001：159－161.

Effect of Atom ic Density on Propagation and Spectral Property of Fem tosecond Gaussian Pulses

WANG Zhendong1，YANG Shanying2，LIU Tingting1，MA Jianling1，XIAO Jing1
（1．School of Physics and Electronics Engineering，Taishan University，Taian 271021，China；
2．Laiwu Vocational and Technical College，Laiwu 271100，China）

We investigate effect of atomic densities（N）on propagation and spectral property of femtosecond Gaussian pulses in a three⁃levelΛ－type atomic medium by using numerical solution of full Maxwell⁃Bloch equations.It is shown that，for pulses with smaller area 2π，propagate inmediumswith different N，pulse splitting does notoccur and strength of spectral componentnear central frequency decreases considerably as N increases.For pulseswith area 4π，pulse splitting could occur when pulses propagate in dilute medium with greater atomic density and in densemedium，and pulse spectral bandwidth and strength of spectral componentwith higher frequency increase with increasing of N in dilutemedium.Spectrum broadening in densemedium ismuch smaller than that in dilute medium with greater atomic density.For pulses with larger area 8π，pulse splitting is similar to that of 4πpulses.Pulse spectral bandwidth and strength of spectral component with higher frequency increase monotonously with increasing of N.And spectrum broadening in densemedium ismuch larger than that in dilutemedium with smaller atomic density.

femtosecond Gaussian pulse；atomic density；propagation；spectrum

O437

A

2013－11－30；

2014－04－12

山东省自然科学基金（ZR2011AL011和ZR2009FZ006）资助项目

王振东（1965－），男，博士，教授，主要研究领域为非线性光学及激光物理和强场物理，E⁃mail：wzd1556＠126.com

Received date： 2013－11－30；Revised date： 2014－04－12