页岩气藏渗流机理及压力动态分析
杜殿发,王妍妍,付金刚,孙召勃,乔 妮(中国石油大学(华东)石油工程学院,山东青岛 266580)
文章编号:1001⁃246X(2015)01⁃0051⁃07
页岩气藏渗流机理及压力动态分析
杜殿发,王妍妍,付金刚,孙召勃,乔 妮
(中国石油大学(华东)石油工程学院,山东青岛 266580)
针对页岩气藏的特点,分析国内外对解吸、扩散等数学描述方法,建立三种机理作用下的渗流数学模型:①考虑有机基质表面解吸,解吸气和游离气共同窜流的数学模型;②考虑有机基质解吸和扩散的数学模型;③考虑有机基质中的气体解吸、扩散,以及无机基质中气体窜流综合作用的数学模型.运用点源函数方法,得到模型的基本点源解,对点源解作积分变换得到垂直压裂井、压裂水平井两种开采方式下的地层压力解,绘制出三种机理影响下的压力动态曲线,并从渗流机理上分析曲线特征以及不同曲线存在差异的原因.
页岩气藏;渗流机理;渗流模型;试井分析
0 引言
目前对页岩气藏渗流机理的研究已越来越深入,已有的渗流数学模型对页岩气藏进行压力动态分析研究,得到了比较符合页岩气藏渗流规律的结果[1].但是由于页岩气藏渗流介质十分复杂,存在有机基质、无机基质、天然微裂缝、大的裂缝等多种孔隙介质,导致渗流机理研究上存在着很大的争议.一般认为吸附气在气藏中占很大比例,但以美国福特沃斯盆地Barnett页岩气藏为代表,解吸气量远少于游离气量,因此气体进入裂缝系统的方式也需要依具体气藏实际情况而定.另外,即便是吸附气量较大,解吸作用在使孔隙内气体浓度增大的同时也必然使压力增大,因此浓度差引发的扩散和压力差导致的渗流在页岩气流动过程中起的作用也没有定论.针对这些问题,本文考虑不同的渗流机理,建立与之对应的数学模型,并在此基础上进行压力动态分析.
1 渗流机理及数学模型
为简化求解,对不同渗流机理下模型作如下规定:①解吸作用符合Langmuir等温方程,解吸作用仅发生在有机基质表面;②扩散作用符合Fick拟稳态扩散定律;③气体流动为单相流,渗流过程等温;④储层各向同性,外边界为无限大;⑤忽略毛管力和重力影响.
1.1 考虑基质解吸、窜流机理的数学模型
该模型适用于气藏开采后期,吸附气含量较少的气藏.模型认为页岩气藏属于基质-裂缝双重介质油藏,渗流分为以下三个阶段:
1)气井开井生产,地层压力下降,气体在有机质表面向内解吸,进入基质孔隙内;
2)基质孔隙内气体量的增加导致压力升高,解吸的气体与游离气体混合在一起,在压力差的作用下从基质孔隙窜流进入裂缝系统;
3)裂缝中的气体在流体势的作用下遵循达西定律流向井筒.
由于解吸的气体会进入基质孔隙,与基质孔隙内部的游离气混合,其作用相当于增加了基质系统的储容能力.因此可以通过增加基质弹性储容系数的方式定量描绘解吸的气体量.此处认为解吸的气体量使得基质系统等温压缩系数增加[2],此时渗流微分方程为-
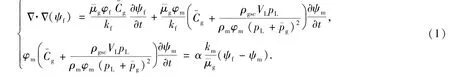
为了降低方程的非线性,许多参数采用了地层平均压力下的值,选择以下公式[3]

引入参数
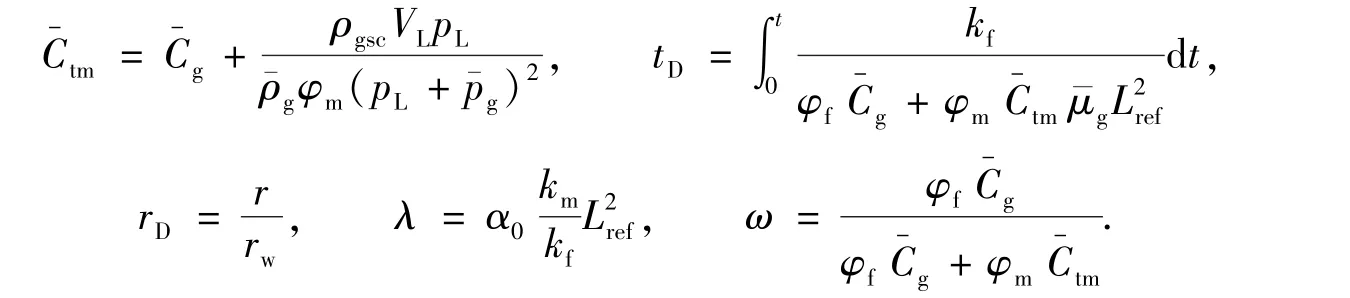
对方程进行化简,并进行Laplace变换,最终得到:
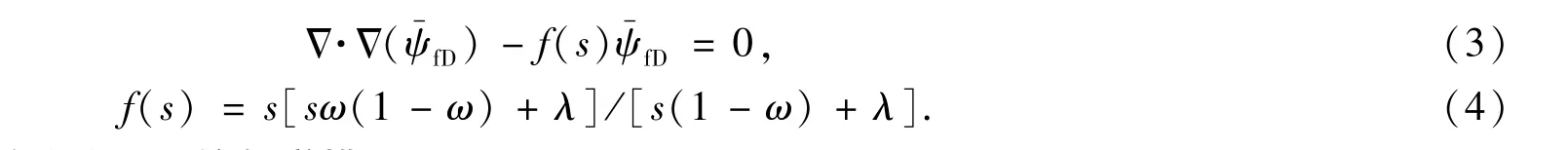
1.2 考虑基质解吸、基质扩散机理的数学模型
该模型适用于有机质孔隙均比较发育、刚投入开发且吸附气含量比较多的气藏.认为页岩气藏属于基质-裂缝双重介质油藏,将页岩气渗流过程描述为以下3个阶段[4]:
1)气井开始生产,地层压力下降,页岩气在基质表面发生解吸,解吸的气体进入基质孔隙;
2)基质孔隙内的气体浓度大于裂缝系统,气体在浓度差的作用下扩散进入裂缝系统;
3)裂缝中的气体在流体势的作用下遵循达西定律流向井筒.考虑了解吸和扩散作用的渗流数学模型为[5]
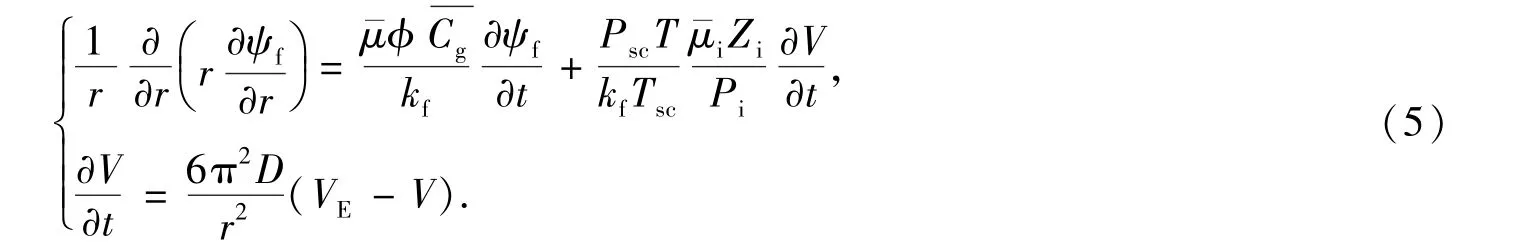
定义一组无因次参数
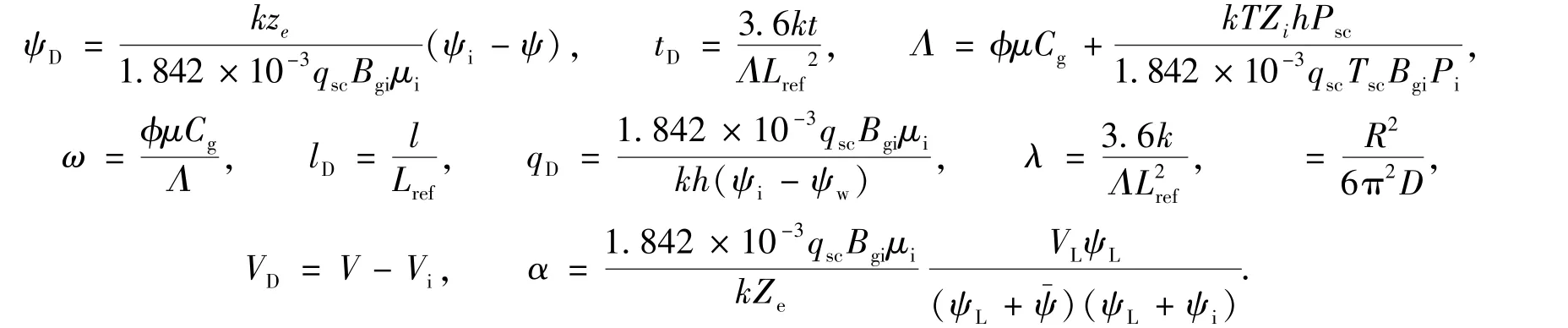
模型无因次化后进行Laplace变换,可得
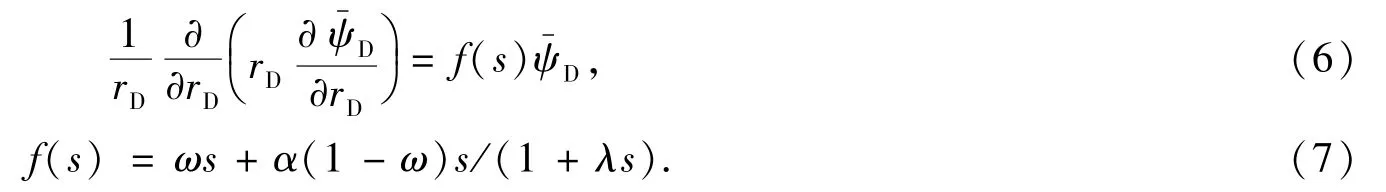
1.3 考虑窜流、扩散综合作用的数学模型
此模型认为页岩气藏的基质孔隙可以细分为有机和无机孔隙两种类型,属于三重介质[6],扩散、窜流分开考虑,是一般化的模型,适用范围较广.渗流过程可分为
1)气井开始生产后,地层压力下降,气体在有机质表面向内解吸,进入有机质孔隙;
2)解吸的气体使得有机质孔隙内气体浓度增大,在浓度差的作用下气体扩散进入裂缝系统;
3)无机基质孔隙内存在的游离气在压力差作用下窜流进入裂缝;
4)裂缝中的气体在流体势的作用下遵循达西规律流向井筒.引入拟压力后,该渗流机理下对应的渗流方程为
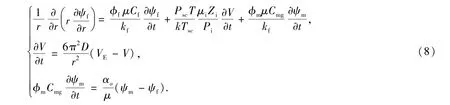
进行无因次化时,需要将上一个模型中的部分无因次参数重新定义
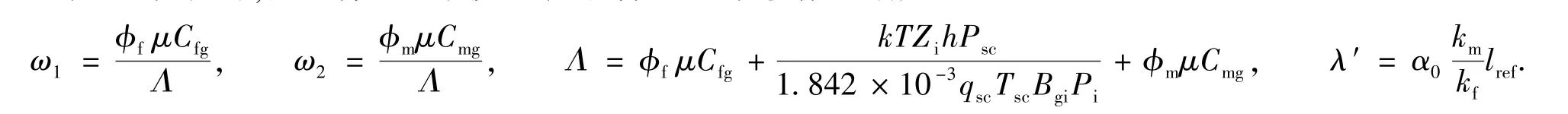
模型化简为
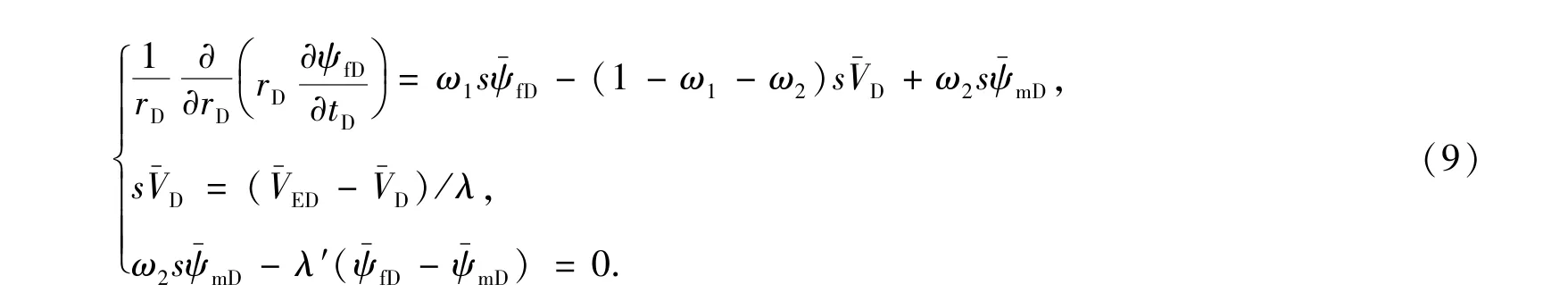
进行Laplace变换得
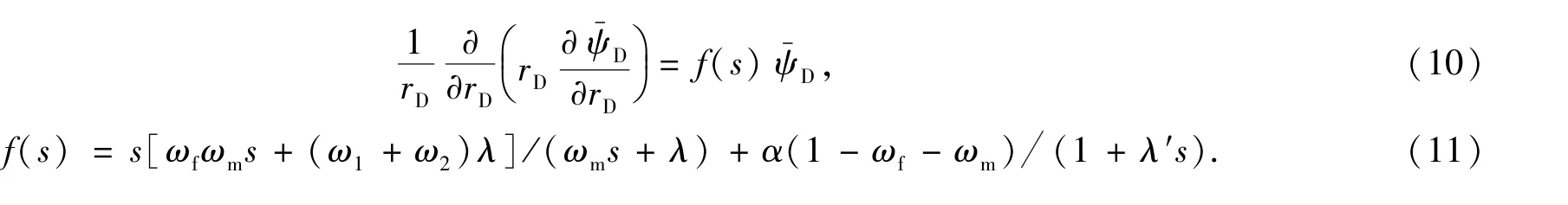
2 点源解的求取
通过引入各自不同的参数对上述三种模型化简,最终模型对应的基本形式一致.根据点源函数的基本理论[7-9]可直接写出三种情况下点源产生的压力响应公式.
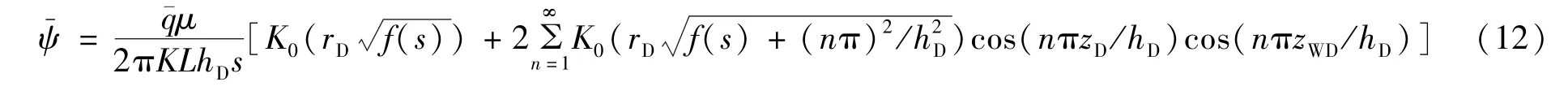
针对不同的渗流机理只需将f(s)进行替换即可.
3 垂直裂缝井模型
3.1 模型假设
模型的假设条件主要包括:①油藏上下为不渗透边界,外边界考虑成无限大情况;②裂缝两翼对称,沿井轴均匀分布,并且完全压开气层,裂缝半长为yf,缝高等于气层厚度h,裂缝为无限导流能力裂缝,中心在(xw,yw,zw)处.其余假设均符合点源解推导时的规定.
3.2 垂直裂缝井压力响应
若裂缝为均匀流量模型,可将点源压力响应沿缝高和缝长方向积分,得到垂直裂缝井压力响应,并将流量进行无因次化,最终得到(lref=yf):

式(13)是Laplace空间中垂直裂缝井在地层中任意一点产生的压力响应,通过数值反演[10]可得到井底压力响应.根据无限导流能力裂缝模型与均匀流量模型的关系,上式中yD=0.732处的压力即可看作是无限导流能力裂缝模型的井底压力.
4 压裂水平井模型
4.1 模型假设
模型的示意图如图1,假设条件主要包括:①油藏上下为不渗透边界,外边界无限大;②一口水平井(长度为L)被不可变形的横向裂缝(条数n,且为单数)垂直贯穿,裂缝两翼对称,沿井轴均匀分布,并且完全压开气层,裂缝半长为yf,缝高等于气层厚度h,裂缝为无限导流能力裂缝.其余假设均符合点源解推导时的规定.
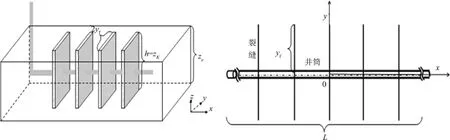
图1 压裂水平井及坐标示意图Fig.1 Fractured horizontal well and coordinate system
4.2 压裂水平井压力响应
以水平无限大油藏为例,对于均匀流量模型,第j条裂缝的流体流动对第i条裂缝上的某一点(xDi,yDi)产生的压力响应为在每条裂缝上另yD=0.732,可近似得到无限导流能力裂缝井底不稳定压力响应[11].
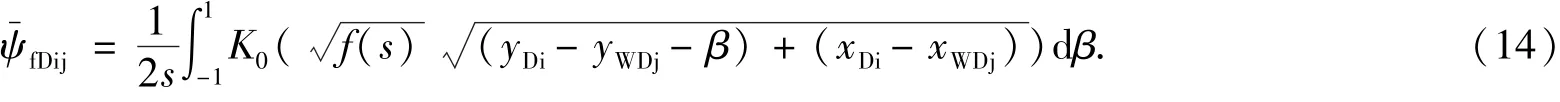
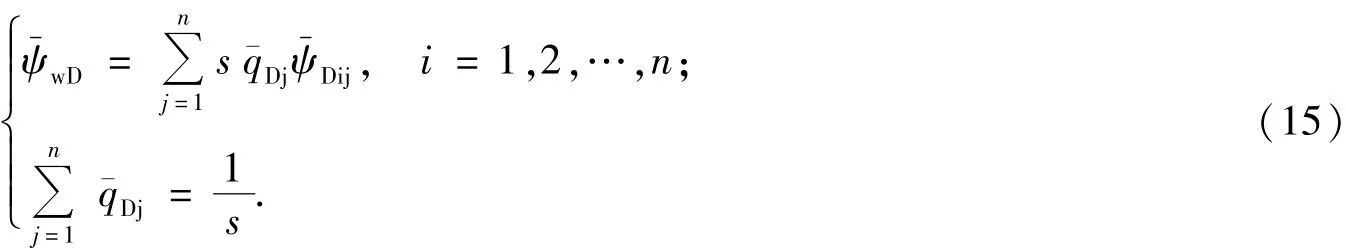
上式可写出n+1个方程,需要求解n+1个未知数,即n个qDi和1个.对于其他类边界的油藏,可用类似的方法得到井底压力解[12].如需考虑井筒存储效应和表皮系数,则可根据如下公式[13]
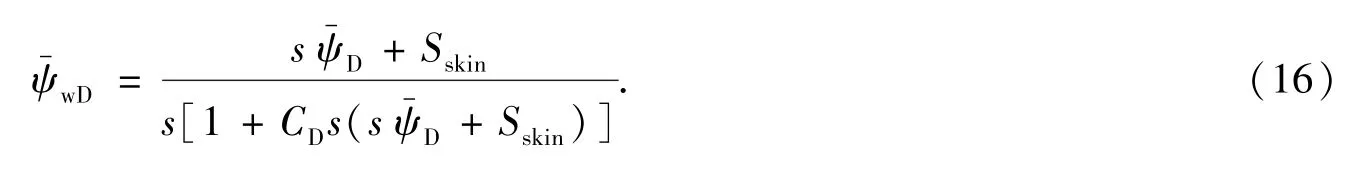
5 压力动态分析
5.1 垂直压裂井压力动态
根据第3部分编程可绘制出页岩气藏中垂直压裂井的压力动态响应,如图2.
分析图2发现井筒存储效应过后,出现裂缝线性流,继而出现两个凹陷段,最终达到边界反应阶段.三种机理下压力动态曲线的区别体现在窜流阶段.前两种机理与双重介质油藏压力动态曲线类似,第三种渗流机理下曲线出现两个“凹子”,表现出三重介质特点[14].
分析三种模型的渗流机理,初期阶段采出的均是裂缝中的游离气,窜流和扩散现象还未显现,三种模型的压力动态曲线重合;随着裂缝中游离气的采出,裂缝和基质之间出现压力差和浓度差.机理1认为解吸的气体与原基质内气体混合,压力差作用下窜流进入天然裂缝,补充裂缝中的气体,使得压力导数曲线最先出现“凹子”,机理3也考虑到了窜流作用,但是由于它将基质细分成了无机基质、有机基质两种类型,仅无机基质中的气体发生窜流作用,因此与机理1相比,“凹子”更浅、更窄,而且出现的时间略晚;接下来扩散作用出现,机理2对应的曲线出现“凹子”,与机理2的曲线相比,机理3曲线的第二个“凹子”较小,出现时间也略晚,原因与前一阶段类似,也是由于基质考虑方式不同引起的.
5.2 压裂水平井压力动态
压裂水平井在页岩气藏开采中占有十分重要的地位,对其压力动态做详细分析.由于第三种模型将解吸、吸附、扩散全部考虑在内,以第三种渗流机理为基础,分析页岩气藏压裂水平井的压力动态,如图3.分析发现压力动态曲线分为7个阶段:①井筒存储阶段;②过渡阶段;③裂缝之间地层线性流阶段;④裂缝之间地层拟径向流动阶段(该阶段只有在裂缝间距取得较大时出现,为一纵坐标为(1/2n)的水平线,此处裂缝条数n=5);⑤扩散、串流阶段(图中两种作用出现的时机相近,“凹子”重合.);⑥地层整体线性流动阶段;⑦地层整体拟径向流动阶段.
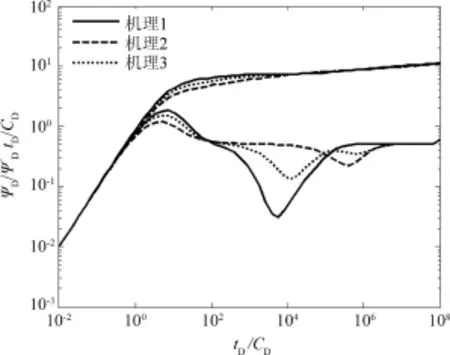
图2 无限大边界页岩气藏垂直压裂井压力动态曲线Fig.2 Typical curves for vertical fractured well in shale reservoir with infinite boundary
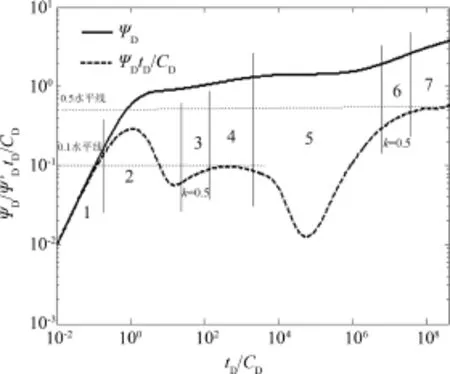
图3 无限大页岩气藏中压裂水平井压力动态曲线Fig.3 Typical curves for fractured horizontalwell in shale reservoir with infinite boundary
由于裂缝间距等取值的不同可能会使得“凹子”出现的时间发生变化,即可能出现在裂缝径向流之后、地层线性流之后或其它时期.如图4,降低了裂缝间距,与图3不同,“凹子”出现在地层线性流阶段之后.分析压裂水平井的压力动态,三种机理的压力曲线在除井筒存储以及边界反映阶段以外的其它阶段均有所不同,其原因与垂直压裂井模型类似,是由于基质类型不同导致了渗流机理出现差异,使得压力导数曲线出现多次交叉.但是不同机理作用下的压力曲线的趋势大体相似.
对于垂直压裂井和压裂水平井,扩散系数、解吸系数、窜流系数的取值不同可能会改变两个“凹子”的大小以及出现的先后顺序.以压裂水平井为例,通过改变解吸系数的值,得到图5所示结果.
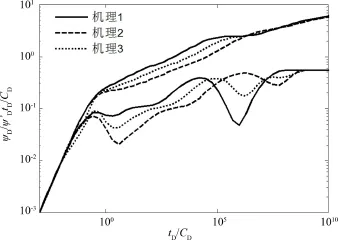
图4 不同渗流机理下压裂水平井的压力动态曲线Fig.4 Typical curves for fractured horizontalwellwithdifferent seepagemechanisms
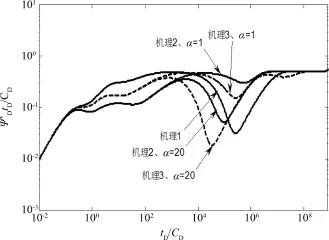
图5 解吸系数对压力导数曲线影响Fig.5 Effect of desorption coefficient on pressure derivative curves
分析机理1和机理2所对应曲线中“凹子”出现的时机,发现系数变化时,机理1的曲线不发生变化,α=1,机理1的模型先出现“凹子”,此时先发生窜流作用,且窜流作用较弱,“凹子”较小;α=20时,机理2对应的模型先出现“凹子”,发生扩散作用,且扩散作用较强,“凹子”较大.对于机理3,发现当解吸系数取某一值时(α=20),两个“凹子”重合,且两个作用叠合使“凹子”最大.
6 结论
1)页岩气藏存在着解吸、扩散、渗流等多种形式的气体的流动,复杂的渗流机理造成了数学描述方法的差异,在分析不同的流动方式对渗流方程的影响的基础上建立了三种渗流数学模型.
2)三种数学模型的不同点主要体现在窜流项上,将其融合在f(s)表达式中,模型可化简成同一种形式,利用常规油气藏的求解方法可写出页岩气藏的地层压力解.
3)根据源函数的基本理论写出了无限大油藏的点源解,通过积分得到了垂直压裂井和压裂水平井的井底压力表达式,编程绘制了压力动态曲线,着重分析了压裂水平井的压力动态,分析得出三种模型压力动态曲线的主要区别出现在窜流阶段.
7 参数说明
ψ:拟压力,Pa;φ:裂缝系统孔隙度;k:裂缝系统和基质系统孔隙度,m2;Cg:气体等温压缩系数,Pa-1;ρg:气体密度,kg·m-3;VL:Langmuir体积,sm3·m-3;pL:Langmuir压力,Pa;pgi:初始压力,Pa;:修正的综合压缩系数,Pa-1;t:时间,s;r:径向距离,m;a:权重系数,可取0.1;λ′:窜流因子;α0:形状因子;Lref:参考长度,m;ω:弹性储容比;pg:气藏压力,Pa;μ:气体粘度,Pa·s;Z:气体压缩因子;T:温度;V:浓度,sm3/m3;D:扩散系数,m2·s-1;Bg:气体体积系数;q:流量,m3·s-1;α:解吸系数;s:Laplace变量;:解吸时间,s;n:裂缝条数;下标说明:f:裂缝系统;m:基质系统;sc:标准状况;w:井底;D:无因次参数;i:初始时刻.
[1] Duan Yonggang,WeiMingqiang,Li Jianqiu,et al.Shale gas seepagemechanism and fractured wells'production evaluation [J].Journal of Chongqing University,2011,34(4):62-66.
[2] Chao Gao,John LeeW.Modelingmultilayer gas reservoirs including sorption effects[C].SPE Eastern Regional Meeting,8 -10 November,1994,Charleston,West Vinginin:Paper SPE29173,1994.
[3] Bumb A C,Mckee C R.Gas well testing in the presence of desorption for coalbed methane and Devonian shale[J]. SPE15227,1998,3(11):179-185.
[4] Duan Yonggang,Li Jianqiu.Transient pressure analysis of infinite conductivity fractured wells for shale gas[J]Natural Gas Industry,2010,30(3):26-29.
[5] Ren Junjie,Guo Ping,Wang Delong,etal.Productivitymodelof fractured horizontalwells in shale gas reservoirs and analysis of influential factors[J].Journal of Northeast Petroleum University,2012,36(6):76-81.
[6] Cheng Yuanfang,Dong Bingxiang,Shi Xian,et al.Seepagemechanism of a triple⁃porosiy/dual permeability model for shale gas reservoirs[J].Natural Gas Industry,2012,32(9):44-47.
[7] Gringarten A C,Ramey H J.The use of source and green function in solving unsteady state problems in the reservoirs[J]. SPE3818,1973,13(5):285-296.
[8] Ozkane,Raghavanr.Some new solutions to solve problems in well test analysis:Part 1⁃Analytical considerations[J].SPE Formation Evaluation,1991,6(3):359-368.
[9] Ozkane,Raghavanr.Some new solutions to solve problems in well testanalysis:Part2⁃Computational considerations[J].SPE Formation Evaluation,1991,6(3):369-378.
[10] Tong Dengke,Chen Qinlei.Some annotation about Stehfest numerical inversion[J].Acta Petrolei Sinica,2001,22(6):91 -92.
[11] Lian Peiqing,Cheng Linsong,Cao Renyi,et al.A coupling model of low permeability reservoir and fractured horizontal wellbore in nonsteady state[J].Chinese JComput Phys,2007,27(2):203-210.
[12] Chen Linsong,Pi Jian,Lian Peiqing,et al.A computationalmethod for productivity of horizontal well in naturally fractured reservoirs[J].Chinese JComput Phys,2011,28(2):230-236.
[13] Brown M,Ozkan E,et al.Practical solutions for pressure transient responses of fractured horizontal wells in un⁃conventional reservoirs[J].SPE125043,2011,14(6):663-676.
[14] Zhao Dongmei,Yao Jun,Wang Zisheng.The pressure⁃transient characteristics of a stress⁃sensitive triple⁃medium reservoir [J].Chinese JComput Phys,2005,22(5):444-448.
Shale Gas Seepage M echanism and Transient Pressure Analysis
DU Dianfa,WANG Yanyan,FU Jingang,SUN Zhaobo,QIAO Ni (College ofPetroleum Engineering in China University ofPetroleum,Shandong Qingdao 266580,China)
According to characteristic of shale gas reservoir,mathematical description methods of diffusion and desorption are analyzed.Three seepage models controlled by different kinds of seepage mechanisms are built:① a mathematical model which considers diffusion and interporosity of desorbed gas and free gas,②amathematicalmodelwhich considers desorption and diffusion,③amathematical model which considers desorption and diffusion in organic porosity and interporosity in inorganic porosity.With modified Lord Kelvin point source function pressure solutions are botained.With corresponding transformation for point source functions,formation pressure solutions for vertical fractured well and fractured horizontal well are obtained and typical curves are shown.At last,characteristics of different curves and threemechanisms'influences on pressure are analyzed.
shale reservoir;seepagemechanism;mathematicalmodel;well test analysis
TE33
A
2013-12-30;
2014-06-13
中国石油科技创新基金(2011D⁃5006⁃0210)资助项目
杜殿发(1972-),男,博士,教授,主要从事油气田开发等研究及教学工作,E⁃mail:dudf@upc.edu.cn
Received date: 2013-12-30;Revised date: 2014-06-13

