固化促进剂用量对集成电路封装环氧模塑料固化行为的影响*

杨明山，李 光，张 卓，冯徐根，金洪广4

（1 北京石油化工学院材料科学与工程学院，特种弹性体复合材料北京市重点实验室，北京102617；2 北京化工大学材料科学与工程学院，北京 100029）

随着微电子技术以及集成电路封装技术的发展，环氧模塑料(EMC)作为电子封装关键材料，得到了快速的发展。环氧模塑料的主要成分为环氧树脂、固化剂、固化促进剂和填料等。其中，固化剂起交联的作用，环氧树脂只有在固化剂存在的条件下才可能打开环氧键，形成稳定的三维网状结构。环氧树脂与大部分固化剂反应都需要在较高温度下才能发生固化交联，为了降低固化反应温度、缩短固化反应时间，需要在环氧模塑料中加入固化促进剂，固化促进剂主要有胺类、咪唑类、膦类[1-3]。固化促进剂用量对集成电路封装用环氧树脂模塑料的封装工艺和固化后的性能具有重要的影响。本文采用非等温DSC 法对环氧模塑料的固化行为进行了研究，为环氧模塑料的配方优化和集成电路封装工艺的确定提供基础数据。

1 实验部分

1.1 主要原料

邻甲酚醛环氧树脂：JEN-801，溴化环氧树脂：EB-400，江山江环化学工业有限公司；酚醛树脂：A002-34，连云港市中和科技有限公司；三氧化二锑：天津市福晨化学试剂厂；硅微粉：DRG-600，连云港东海硅微粉有限责任公司；硅烷偶联剂：WD-60，武汉武大有机硅材料有限公司；巴蜡：巴蜡1 号，巴西进口；2-甲基咪唑：广州市固研电子材料有限公司。

1.2 主要仪器设备

高速混合机：SHR10B，张家港市轻工机械有限公司；双辊开炼机：IR502，东莞市台锐仪器有限公司；动态差示扫描量热仪：DSC-60，日本岛津公司。

1.3 试样制备

以表1 的配方称量各组份，放入高速混合机中，高速混合20s，静置1min，连续混合3 次。然后采用双辊开炼机进行混炼，温度90℃~100℃，开炼时间3min~5 min，辊速比1.0，1.2[(前)：(后)]。双辊开炼后冷却，经过粗粉碎、细粉碎，然后过孔径为150 μm 的网筛，进行测试。

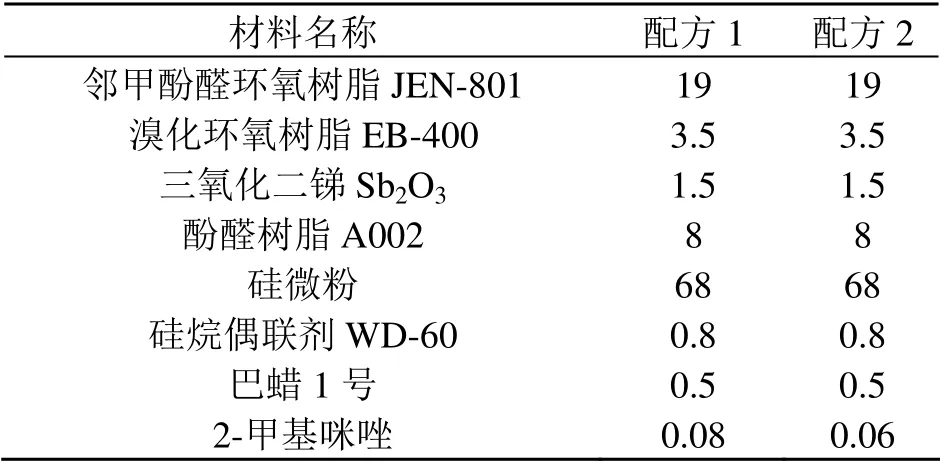
表1 实验配方 Table 1 The experimental recipe

1.4 性能测试

利用动态差示扫描量热仪测试样品的非等温固化行为。称取3mg~5mg 待固化样品于铝坩埚中，压盖，用空白铝坩埚作参比。温度范围30℃~250℃，升温速率分别为5℃/min、10℃/min、15℃/min、20℃/min，得到样品DSC 曲线图。测试在氮气保护下进行，流量为50mL/min。

2 结果与讨论

2.1 实验原理

环氧模塑料固化反应为放热反应，在DSC 曲线上会出现固化放热峰，该放热峰的起始温度Ti、峰值温度Tp和终止温度Te随升温速率的增大逐渐向高温方向移动。这主要是因为升温速率增大，dH/dt增大，即单位时间内放出的热量多，产生的温差大，表现为放热峰向高温移动。

用非等温DSC 分析环氧树脂模塑料的固化动力学，可采用Kissinger 法、Crane 法和Ozawa 法。利用不同升温速率下固化峰的峰值温度Tp，就可以对固化动力学参数进行计算。

Kissinger[4]法是进行固化动力学处理时常采用的方法。Kissinger 方程中，峰值温度与升温速率的关系为：

式中，升温速率常数β=dT/dt，单位℃/min；Tp为DSC 曲线上放热峰的峰值，单位K；A 为指前因子；R 为理想气体常数8.314J/(mol·K)；Ea为固化活化能(J/mol)。

反应级数是反应复杂与否的宏观表征，通过反应级数的计算可简单地判定反应过程的复杂程度，及粗略地估计固化反应机理。反应级数n 可用Crane[5]方程计算：

其中，C 为常数，n 为反应级数。以-lnβ 对1/Tp作图，通过线性拟合可得直线斜率 Ea/nR，将Kissinger 法计算出的活化能Ea带入，进而可求得固化反应级数n。

固化反应的活化能也可由Ozawa[6]方程得到：

式中G(α)是与转化率有关的函数。

以-lnβ 对 1/Tp作图，经拟合得直线斜率1.0516Ea/R，由此可计算出固化活化能Ea。

2.2 不同固化促进剂用量EMC 的固化活化能

图1 为两个配方样品在不同升温速率下的DSC曲线，固化温度数据见表2。

图1 两个配方EMC 在不同升温速率下的DSC 曲线 Fig 1 The DSC curves of two EMCs

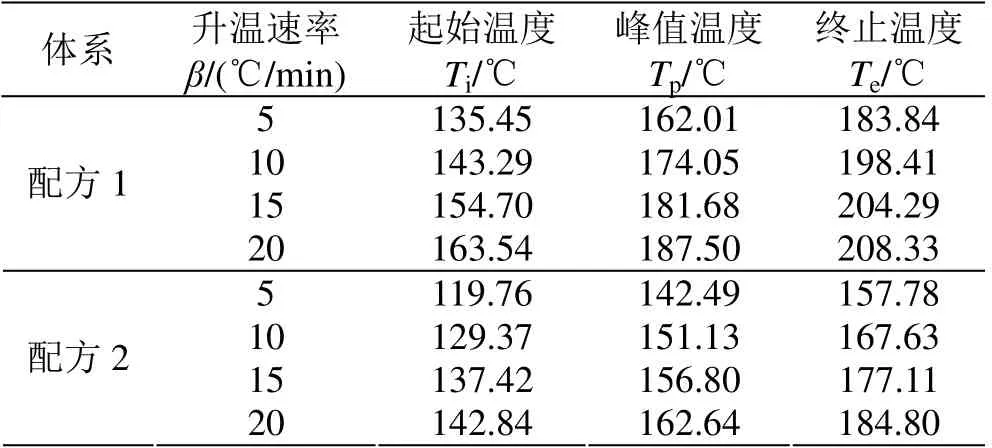
表2 两个配方样品在不同升温速率下固化温度数据 Table 2 The DSC curing data of two EMCs at varied increasing rate of temperature

2.2.1 Kissinger 法计算固化活化能

根据表2 数据，以ln(Tp2/β)对1/RTp作图，见图2，通过线性拟合计算直线斜率k，可求得固化活化能Ea。

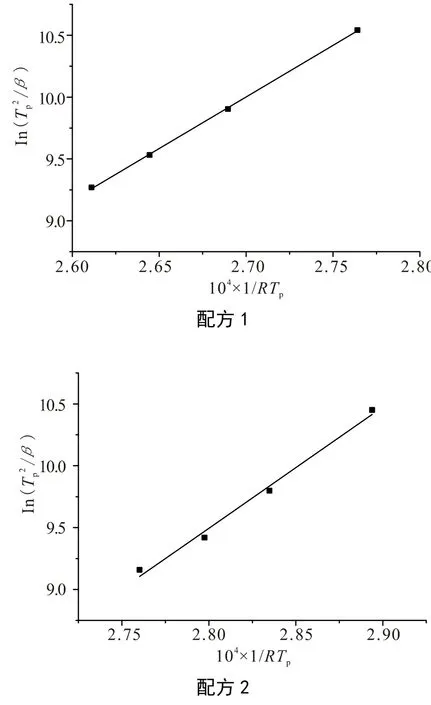
图2 ln(/β)与1/RTp拟合直线 Fig. 2 The curves of ln(/β)-1/RTp

通过对比固化促进剂2-甲基咪唑的用量对环氧模塑料固化行为的影响，发现2-甲基咪唑用量高的体系，其反应的固化活化能明显小于2-甲基咪唑用量低的体系，这说明增加固化促进剂的用量可以降低固化活化能，其体系更容易发生反应。

2.2.2 Ozawa 法计算固化活化能

根据表2 数据，以-lnβ 对1/Tp作图，见图3，经拟合得直线斜率1.0516Ea/R，由此可计算出固化活化能Ea，0.08 份2-甲基咪唑体系的活化能为86.385kJ/mol，含0.06 份2-甲基咪唑体系活化能为99.895kJ/mol。

通过Ozawa 法计算出固化活化能的结果与Kissinger 法计算固化活化能的结果相比较，数值上有些许不同，但整体范围和趋势不变，即增加固化促进剂的用量可以降低体系的固化活化能。

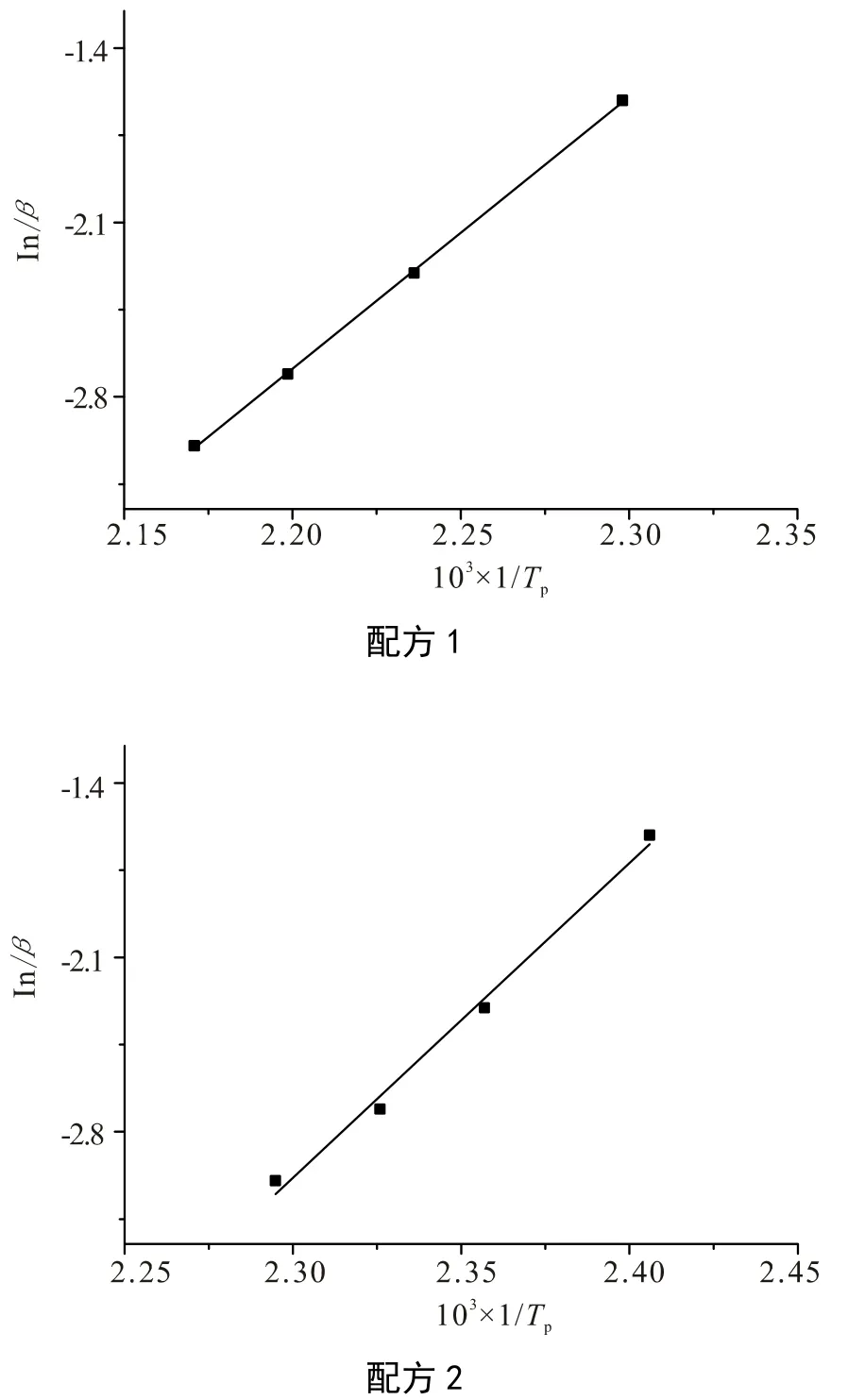
图3 -ln(β)与Tp 拟合直线 Fig. 3 The curves of -ln(β)-Tp

2.2.3 Crane 法计算反应级数

根据表2 数据，以-lnβ 对1/Tp作图，见图3。通过线性拟合可得直线斜率Ea/nR，将Kissinger 法计算出的活化能Ea带入，进而可求得固化反应级数n。

含0.08 份2-甲基咪唑体系的反应级数为0.932，含0.06 份2-甲基咪唑体系的反应级数为0.920。两种固化体系的反应级数比较接近，在简化处理的前提下其固化反应都接近于一级反应，由此可以看出，固化促进剂用量对反应级数影响很小。

2.3 固化工艺的确定

环氧树脂模塑料在一定固化工艺下进行固化反应，其固化程度对性能有较大影响。固化程度越高，热性能越好。不同升温速率下的体系起始温度Ti、峰值温度Tp和终止温度Te，对不同升温速率下的3个温度值进行线性回归，外推得到升温速率为0 时的固化起始温度、峰值温度和终止温度，从而可以确定环氧树脂模塑料的最佳固化温度范围，初步确定固化工艺。

根据表2 的DSC 实验数据，分别以放热峰的Ti、Tp和Te对升温速率β 作图，如图4 所示。经线性拟合外推至β=0℃/min，可得固化过程中的凝胶化温度，固化温度，后固化温度，结果列于表3。

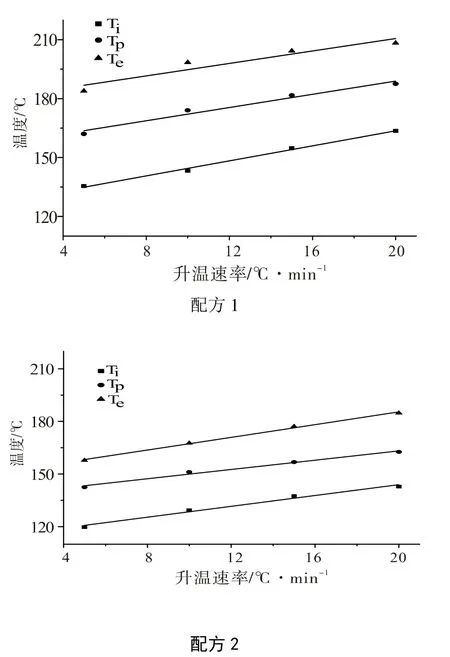
图4 Ti、Tp 和Te 与升温速率的关系曲线 Fig. 4 The curves of curing temperature vs increasing rate of temperature

表3 环氧模塑料的固化工艺参数 Table 3 The curing parameters of EMCs

从表3 可以看出，配方2 的固化特征温度均较配方1 的低，而配方2 中固化促进剂的用量却比配方1 中的低，其固化特征温度理应比配方1 高，但表3 数据却相反，原因在于两个配方的预交联程度不同。

以环氧模塑料的单位质量固化放热值对升温速率β 作图，如图5 所示。经线性拟合外推至β=0℃/min，得出外推放热值，列于表4。

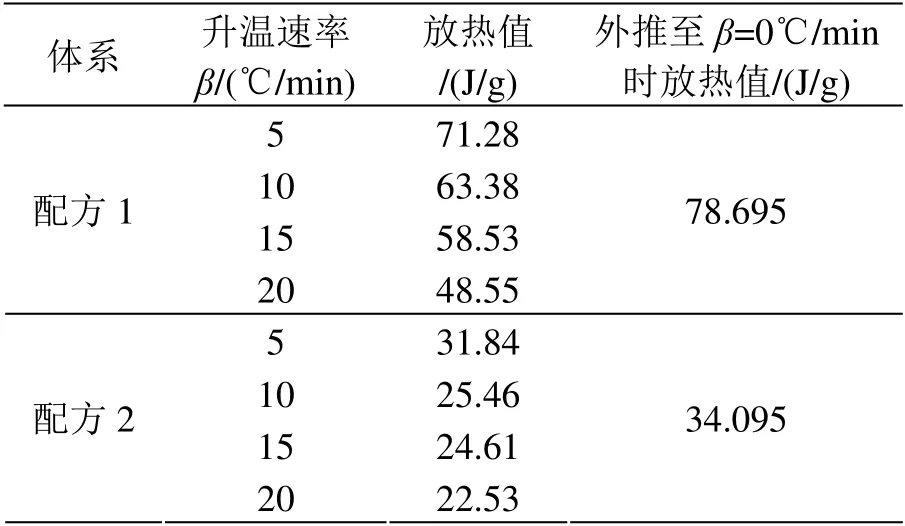
表4 环氧模塑料的固化放热 Table 4 The curing heat of EMCs

图5 放热值与升温速率的关系曲线 Fig. 5 The curves of curing heat vs incresing rate of temperature

外推至β=0℃/min 时的单位质量放热值可以视为样品完全固化所放出的热量值。对比配方1 和配方2 可以发现，配方2 样品的固化放热值明显小于配方1，这是由于两者在制备过程中所采用的预固化时间不同而引起的。配方2 样品使用了较长的预固化时间，其在预固化阶段的固化程度要高于配方1，因此在后期固化过程当中放出的热量较小。

预固化时间对环氧模塑料的固化温度、凝胶化温度和后固化温度也有一定的影响。从表3 可以看出，增加预固化的时间，环氧模塑料的特征温度随之降低。而固化温度即是其封装工艺温度。因此，环氧模塑料的封装工艺温度可以通过改变预固化时间来进行适当调整。

3 结论

对不同固化促进剂用量的环氧模塑料的固化行为进行了非等温DSC 分析，应用Kissinger、Crane和Ozawa 方法获得了反应活化能Ea、反应级数n等固化动力学参数；推导出了固化反应过程的凝胶化温度Ti0、固化温度Tp0和后处理温度Te0，确定了固化工艺；结果表明，增加固化促进剂用量可降低固化活化能，使反应易于发生。

[1]韩江龙. 环氧塑封料现状及发展趋势[J]. 电子工业专用设备，2012(12)：6-9.

[2]孙曼灵. 环氧树脂应用原理与技术[M]. 北京:机械工业出版社，2002：442-473.

[3]亢雅君，殷立新. 环氧树脂中温固化促进剂评述[J]. 热固性树脂，1995(2)：47-51.

[4]Kissinger H E. Reaction Kinetics in Differential Thermal Analysis [J]. Analytical Chemistry，1957，29(11)：1702-1706.

[5]Crane L W，Dynes P J，Kaelble D H. Analysis of curing kinetics in polymer composites[J]. Polymer Letter Edition，1973，11(8)：533-540.

[6]Ozawa T. Kinetic Analysis of Derivative Curves in Thermal Analysis [J]. Journal Thermal Anal，1970(2)：301-324.