“相互作用”的重难点剖析

张健

一、重力

由于地球的吸引而使物体受到的力，叫做重力.它不是地球对物体的吸引力，而是万有引力的一个分力，因而它的方向一般不是指向地心，是竖直向下.而且物体在两极时重力最大，在赤道时最小.一般情况下可认为重力近似等于地球对物体的万有引力.课本对这部分内容作了诠释，在学了必修2的向心力和万有引力定律后可理解它.

二、弹力

发生形变的物体，由于要恢复原状，对与它接触的物体产生力的作用，这种力叫做弹力.要明确弹力的施力物体是发生形变的物体，受力物体是与它接触的物体.分析受力时弹力的有无及方向尤为重要.

1.弹力有无的判断方法

（1）条件法：根据物体是否直接接触并发生弹性形变判断是否存在弹力.此方法多用来判断形变较明显的情况.

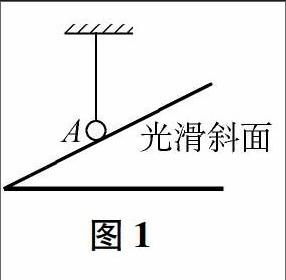
（2）假设法：分析如图1中A球的受力情况.假设4球与斜面间存在弹力，物体不能静止.所以4球只受重力和绳的拉力作用.

（3）状态法：根据物体的运动状态，判断弹力是否存在.图2中所有接触面均光滑，判断汽车刹车时物体A是否受到汽车侧壁的弹力作用.汽车做减速运动，A由于惯性要保持匀速运动，两者之间有挤压，所以A受到汽车侧壁的弹力作用.如果汽车做匀速直线运动，则两者之间无弹力.

2.弹力方向的判断方法

（1）根据物体所受弹力方向与施力物体形变的方向相反判断.

（2）根据共点力的平衡条件或牛顿第二定律确定弹力的方向.

例1 如图3所示，小车上固定着一根弯成α角的曲杆，杆的另一端固定着一个质量为m的球.试分析下列情况下杆对球的弹力的方向.

（1）小车静止；

（2）小车以加速度α水平向右加速运动.

解析（1）根据共点力平衡可知该弹力竖直向上.

（2）小球受重力和杆的弹力两个力，其合力水平向右，如图4所示，，β和α不一定是互余的关系，

杆的弹力方向不一定沿杆的方向.

三、摩擦力

1.静摩擦力方向的判断方法

例2 如图5所示，A、B两物块叠放在一起，在粗糙的水平面上一起向右做减速直线运动，运动过程中B受到的摩擦力方向是________，A受到B的摩擦力方向是____.

我们可试着用假设法（假设接触面光滑）、状态法两种方法判断B受到的摩擦力方向，用牛顿第三定律判断A受到的摩擦力方向.这也是判断静摩擦力方向的三种常用方法.

2.摩擦力大小的计算

（1）滑动摩擦力由公式计算，要注意以下两点：

①μ为动摩擦因数，F_N为两接触面间的正压力，其大小不一定等于物体的重力.

②滑动摩擦力的大小与物体的运动速度、接触面积的大小都无关.

（2）静摩擦力的计算

①它的大小和方向都跟产生相对运动趋势的力密切相关，跟接触面的正压力F_N无直接关系，对具体问题要具体分析物体的运动状态，根据物体所处的状态（平衡、加速等），由力的平衡条件或牛顿运动定律求解.

②最大静摩擦力F_max：是物体将要发生相对运动这一临界状态时的摩擦力.在F_N不变的情况下，F_max比滑动摩擦力稍大些，通常认为二者相等，而静摩擦力在O～F_max间变化.

例3如图6所示，物块A放在倾斜的木板上，木板的倾角α为30°和45°时A所受的摩擦力大小恰好相等，则4和木板间的动摩擦因数为多少？

解析 同学们解这一题时往往无从下手，就是没有分清是静摩擦力还是滑动摩擦力.木板的倾角α为30°和45°时A所受的摩擦力大小恰好相等，不可能同时为静摩擦力或滑动摩擦力，所以α= 30°时A受的是静摩擦力，α= 45°时A受的是滑动摩擦力，即mgsin30°=μmgcos45°，解得

3.摩擦力认识上的两个误区

（1）摩擦力一定是阻力.静摩擦力阻碍的是物体间的相对运动趋势，并不是阻碍物体的运动，它可以是阻力，也可以是动力.例2中如果A、B一起加速运动，则B受的静摩擦力向右，与运动方向相同.同理，滑动摩擦力也不一定是阻力，主要看准“相对”二字.

（2）运动的物体只能受到滑动摩擦力，静止的物体只能受到静摩擦力.例2中，B向右运动，受到的是静摩擦力.在图7中，A在拉力F作用下运动，静止的B受到滑动摩擦力.

判断物体具有“相对运动趋势”或“相对运动”不是以地面为参考系，而是以相互作用的另外一个物体作为参考系，因此静止的物体也可能受到滑动摩擦力，运动的物体也可能受到静摩擦力，

四、合力与分力

当一个物体受到几个力的共同作用时，如果一个力产生的效果跟原来几个力的共同效果相同，这一个力就叫做那几个力的合力，原来的几个力就叫做分力.合力与分力的本质是作用效果相同，它们具有等效替代的关系，遵循平行四边形定则.

1.力的分解的唯一性问题

（1）已知合力F及一个分力的大小和方向，则另一个分力是唯一的.

（2）已知合力F及两个分力的方向，则两个分力的大小是唯一的.因此我们分解力时根据力的作用效果找出两分力方向，两分力大小是唯一的.

（3）已知合力F、一个分力的方向（如分力F1与F的夹角α）和另一个分力的大小F2，求分力F.的大小和F2的方向，有如下几种情况，

①F

②F2=Fsinα时有唯一解.如图9所示.

③Fsinα

④F2≥F时有唯一解，如图11所示.

2.已知两个共点力F1、F2的合力为F，如果它们之间的夹角θ固定不变，当其中一个力F.逐渐增大时，合力F-定增大吗？

（1）当θ≤90°时逐渐增大F1的大小，作出两个力的合力可知，随着F1逐渐增大，F逐渐增大.

（2）当θ>90。时逐渐增大F.的大小，作出两个力的合力如图12所示，当F与F1垂直时F最小，所以当F1从零逐渐增大时，F先减小后增大.

以上分析可知，合力不一定大于分力，合力可以大于、等于或小于分力.

3.正交分解法：将已知力按互相垂直的两个方向进行分解的方法，是一种很重要的分解方法.

建立坐标轴的原则：一般选共点力的作用点为原点.共点力平衡时，以少分解力为原则（即尽量多的力在坐标轴上）；应用牛顿第二定律解题时，一般以加速度方向和垂直加速度方向建立坐标系.

注意力的正交分解是在物体受三个或三个以上的共点力作用下求合力的一种方法，分解的目的是为了更方便地求合力，将矢量运算转化为代数运算.另外，建立坐标系时，一般情况下应尽量使所求量（或未知量）“落”在坐标轴上，这样解方程较简单.