应用于农村配电网的测量点与补偿点分离式无功补偿设备及其优化配置

张之昊 武建文 李 平 史宏伟 张保卫

（1.北京航空航天大学自动化科学与电气工程学院 北京 100191 2.河南电力公司周口供电公司 周口 466000 3.河南电力公司周口供电公司郸城分公司 周口 477150）

1 引言

由于散热、开关管耐压以及成本高等问题，无功功率发生器、晶闸管投切电容器等无功补偿手段在户外10kV 柱上环境应用较少。机械投切电容器（MSC）结构简单、成本低且可靠性高，是户外10kV柱上无功补偿的主要手段。在配电网供电线路中安装MSC 可以有效地提高供电网的电能质量，减小网络损耗，改善电压分布效果[1]。农村配电网多为干线式和放射式分布，线路长、分布广，功率因数偏低，无功补偿需求大，但资金有限，配电网无功优化规划问题得到了深入的研究[2-9]。

目前无功优化规划方法多采用遗传算法等随机搜索算法[10-14]。其最优解通常将无功补偿设备的安装点置于需要补偿的各个无功负荷线路之间，既补偿线路上设备安装点后侧的无功功率，又补偿安装点前侧的无功功率[8,15]。但是目前配电网分布式无功补偿设备大多只能补偿安装点后的无功功率，客观上造成了无功补偿设备与无功优化规划方法之间的偏差。对此，文献[8]提出了电容器优化投切的作用范围法，研究电容器补偿安装点前后无功功率的规划方法问题；文献[15]研究了不均匀主馈线上无功负荷优化配置问题；文献[16]提出用最优覆盖法建立无功补偿优化模型；文献[17]采用了设置比值α(1≤α ≤2)，使设备可以补偿安装点后无功功率的α 倍的方法实现对设备安装点前后无功功率同时补偿。但是在负荷变化频繁的配电网，容易造成无功倒送等问题，比值α 的校正依赖实际线路的数据和工程经验。文献[18]指出全局优化方法在含有大量开关的复杂电力系统中，可通过配电网重构和电容器投切实现配电网最优配置。但是在结构相对简单的农村电网，涉及的配电网重构问题较少，补偿电容器控制范围相对固定，难以发挥配电网重构和电容器投切综合优化的优势。

为了解决无功补偿设备与无功优化规划方法之间存在偏差的问题，本文设计了测量点与补偿点分离的无功补偿设备，讨论了分别确定补偿点和测量点位置的优化方法。针对测量点与补偿点分离的特点，对无功优化规划方法进行了改进和优化。所设计的无功优化规划方法适用于农村电网线路长、分布广、功率因数低并多为主干式和放射式的电网结构。

2 设备结构及原理

测量点与补偿点分离的无功补偿设备包括补偿器和测量器两部分。

2.1 测量点与补偿点分离无功补偿设备工作原理

传统的无功补偿设备补偿器与测量器为一个整体，安装于图1 中补偿器C2位置，只能补偿负荷4的无功功率。采用测量点与补偿点分离的无功补偿设备，测量点和补偿点的安装如图1 中所示，则设备可以同时补偿负荷2、3、4 的无功功率，使补偿器可以安装在各个负荷的中心位置，配置更加合理，进一步降低电网损耗。

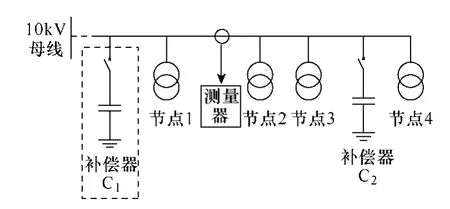
图1 设备原理图Fig.1 Equipment schematics

2.2 补偿器结构及原理

补偿器包括固定电容器、机械开关、投切电容器、控制器以及电源PT 等，结构如图2 所示。

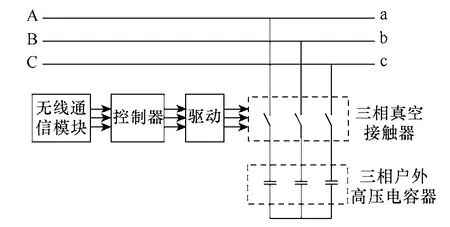
图2 补偿器结构图Fig.2 The compensation part structure

补偿器的控制器通过无线通信模块从测量器获得测量点的三相电压电流、无功功率、有功功率和功率因数等运行数据，根据设置的动作判据，得到控制信号输出给驱动器，驱动三相真空接触器实现对三相户外高压电容器的投切控制。

2.3 无功信号测量器结构及原理

无功信号测量装置由电流互感器、电压互感器、运算单元与无线通信模块组成，如图3 所示。

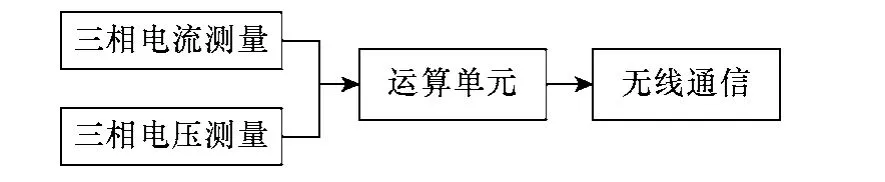
图3 测量器结构图Fig.3 The measurement part structure

测量器采集供电线路测量点的三相电压电流数据，经运算单元计算出供电线路测量点的有功功率、无功功率以及功率因数等数据，由无线通信模块将数据传输给补偿器。无线通信可以采用数传电台、GPRS 通信等方式，综合考虑成本以及安全性等问题，本文在实际实验时采用了GPRS 通信方式，体积小，通信稳定，并且可以实现各台设备数据和运行状态的集中获取与控制。

3 分离式无功补偿设备位置优化配置

分离式的无功补偿设备的无功优化规划与传统的无功优化规划有不同的特点，需要对补偿点与测量点位置选取以及补偿容量等多个方面进行考虑。

3.1 目标函数

考虑到目前配电网分布广、资金有限的实际情况，无功优化规划在满足约束条件的前提下，以年平均降损经济收益最大为目标，目标函数由投资费用CI和降损收益CP两部分组成，目标函数具体模型为

其中，年均投资费用CI的计算方法为

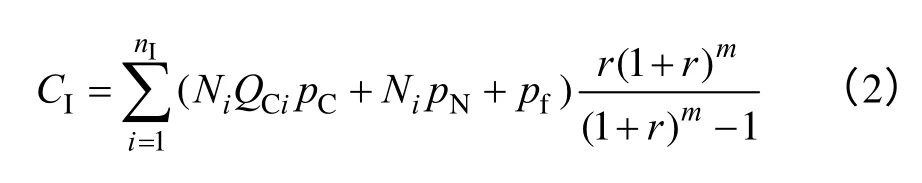
式中，nI为线路中补偿设备套数；Ni为第i 套设备投切电容器的分组数；QCi为线路中第i 套设备单组补偿电容的容量；pC为补偿电容单位容量价格；pN为补偿设备单组价格；pf为每套投切电容器设备的固定费用；r为贴现率；m为设备使用年限。

降损收益CP的计算方法为

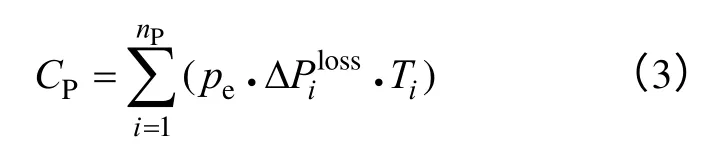
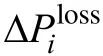
3.2 约束条件

补偿电容容量约束

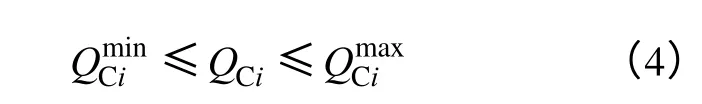
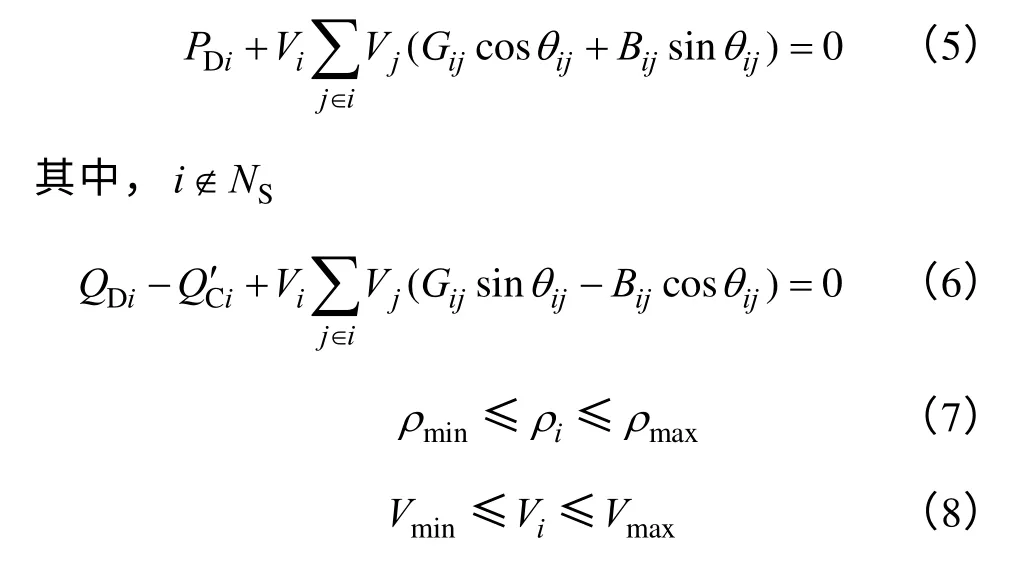
式中，Gij、Bij分别为节点i 和节点j 之间互导纳的实部和虚部；Vi、Vj分别为节点i 和节点j 的电压幅值；Vmin、Vmax为各节点电压的最大与最小值；θij为节点i 和节点j 之间电压相位差；PDi、QDi为节点i 的有功负荷和无功负荷；QC′i为容量为QCi的电容在电网电压水平下实际投入容量；ρi为第i 个设备测量点所测得功率因数，ρmin和ρmax为测量点处允许的功率因数的最小值和最大值。

3.3 求解方法

3.3.1 采用灵敏度分析法确定补偿点选择

灵敏度分析法指对系统潮流方程采用转置雅可比矩阵法求出配电线路各节点对无功注入的灵敏度。10kV 配电网供电线路分布广、线路长且节点众多，将每一个节点作为待选补偿点不符合实际。因此，采用灵敏度分析法。软件编程中提供人工干预接口，以便结合供电线路各节点实际情况，决定待选的补偿点。

3.3.2 测量点选择

遗传算法具有群体搜索、内在启发式随机搜索、可与其他技术混合使用以及可以并行运算等优点，本文采用遗传算法进行无功优化规划计算。测量点的选择对设备的补偿效果有很大的影响。本文分两种情况讨论测量点位置的确定方法。

在配电线路各节点平均负荷较重或者单台补偿设备控制范围较大的情况下，补偿设备控制范围内节点间的电压降落已经不能忽略，需要通过潮流计算确定补偿效果。因此采用将测量点选取融合进遗传算法优化计算过程的方法。

将测量点位置作为遗传算法中每个个体染色体上的基因。其待选测量点安装位置的选取范围由线路上各节点无功负荷、补偿设备每组补偿范围和补偿设备分组数范围决定。补偿设备控制范围内各节点无功负荷之和必须大于补偿设备每组补偿容量最大值与分组数最大值的乘积。如图1 所示，设补偿器C2的最大单组容量与分组数乘积大于节点2、3和4 无功负荷之和，小于节点1、2、3 和4 无功负荷的总和。可知测量点的待选安装点为节点2 和3（测量点安装在节点的近电源侧，如图1 中测量点位置为节点2 的近电源侧）。

遗传算法存在过早收敛的问题，因此利用遗传算法确定补偿设备的补偿容量、分组数和测量点位置时，需要研究运算过程中影响结果和算法稳定性的变量。

功率因数：对于线路中的无功补偿设备，其测量点与其线路远端无功补偿设备的测量点之间为其设计补偿范围。在遗传算法的计算过程中，设备测量点的功率因数在约束范围内，即可保证补偿范围内线路稳定运行。

补偿电容容量和分组数：补偿电容容量和分组数的选取不但要考虑线路对于无功补偿容量的需求，同时要考虑到补偿容量或者分组数。补偿容量或者分组数过大，已投入的电容器分组会导致后续电容器分组投入时产生的过电压和涌流增大；增加设备的体积和重量，甚至超过柱上环境的承重能力；加重系统的非线性，增大遗传算法过早收敛的概率。

设备数量：配电网柱上补偿方式中，同一配电线路上补偿设备数量不宜过多。设备过多会增大无功竞争的风险，同时也会极大增加设备后期维护成本。设备数过多会增大遗传算法中染色体上的基因数，增大运算量，同样也会加重系统的非线性。

电压极限约束：由于测量点与补偿点的分离，使得设备补偿容量增大，补偿点及其附近节点电压会被抬高，甚至高于测量点电压。忽略电网中其他设备的阻抗，可以通过式（10）估算补偿点电压。

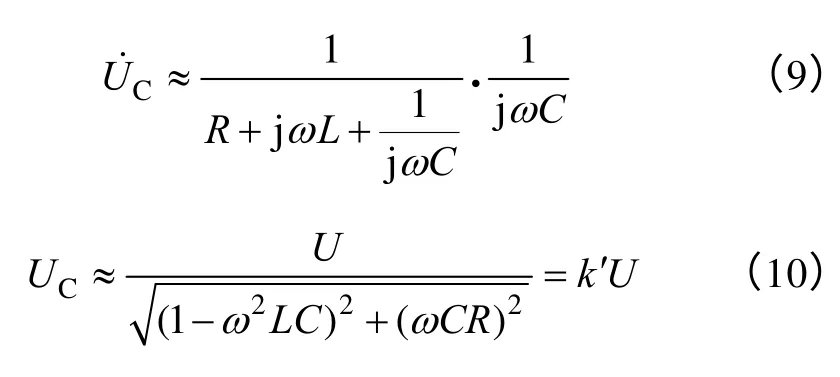
式中，U为测量点电压；UC为补偿点电压估计值；L、R为补偿点与测量点之间的线路电感和电阻值，可根据线路距离估算。设UC=kU，则k 的取值介于k′与1/k′之间。由此可得，保证U 与式（10）算得的UC估计值符合电压约束条件，即可保证补偿点与测量点之间线路符合电压约束条件。也可以通过测量器直接测量电源PT 电压的方法准确获得补偿点电压。但是此种方法只能测量3 个线电压中的一个，不能排除线路不平衡电压的影响。

无功优化规划的方法计算量较大，其主要的问题在于补偿电容的投入影响了电网各节点电压，所以各个节点的状态需要经过复杂的潮流计算。但是在配电线路相邻补偿器距离较近的情况下，节点间导线分布的电感和电阻较小，可忽略两相邻补偿器所在节点间的电压降落（例如图4 中a 节点和c 节点间的电压），对算法进行简化。先通过人工估算，确定测量点位置，再进行无功优化规划。此种情况下仍以图1为例，设补偿器C2的测量器可选节点为节点2 和节点3，则节点2 可由C1或C2补偿。问题简化为计算节点2 的无功功率由补偿器C1或C2补偿损耗更小，忽略无关节点，简化后计算模型如图4 所示。

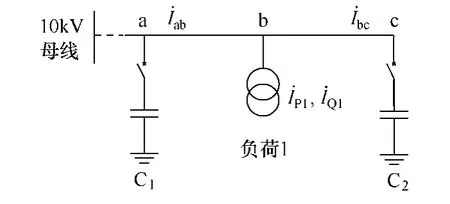
图4 测量点选取示意图Fig.4 The measurement part position determining

电网ab 段，电流Iab，bc 段电流Ibc，b、d 节点无功电流分别为IQ1和IQ2，有功电流分别为IP1和IP2。对比分析分别在a、c 两节点安装的无功补偿设备对b 节点进行无功补偿的效果。

由a 点的无功补偿设备C1补偿b 点的无功功率时，线路损耗ΔPa计算如下

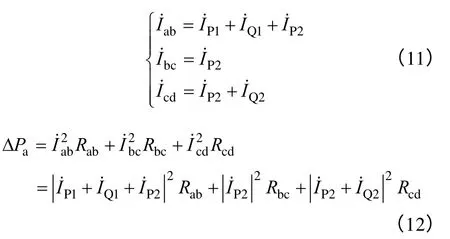
由c 点的无功补偿设备C2补偿b 点的无功功率时，线路损耗ΔPc计算如下

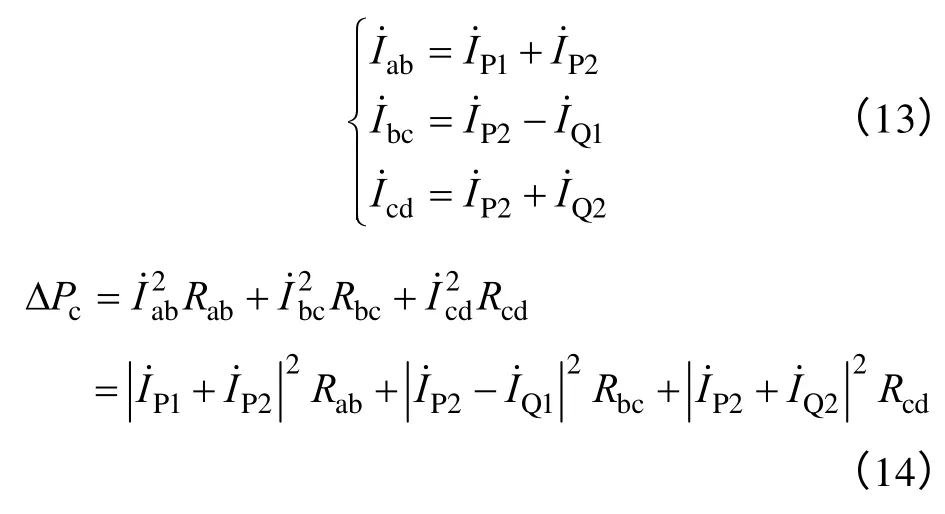
有功电流和无功电流相位差90°，得

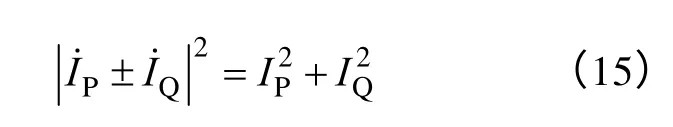
两者对比，由式（12）～式（14），得

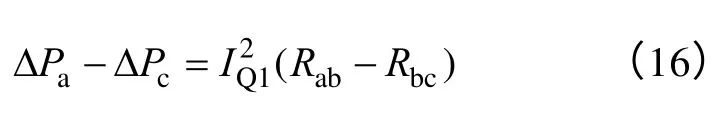
一般认为输电线的电阻值均匀分布，与长度成正比，从式（16）可知，无功负荷应由与其距离最短的无功补偿设备进行补偿，因此，测量点的选取应使得待补偿负荷节点从与其距离最近的补偿器获取无功功率。若节点b 距离节点a 较远，则C2的测量器应置于节点b 前侧，由C2补偿节点b 的无功功率，否则应置于节点b 后侧，由C1补偿节点b 的无功功率。

简化后算法精度分析：如图4 所示，设节点c视在功率为S，相对于相邻补偿器所在节点a 电压降落率为α，节点 a 电压为 U，则节点 c 电压为U·（1-α），节点c 的电流为I，损耗为ΔP。当忽略节点a、c 间电压降落时，节点c 电压按节点a 电压U 估算，此时节点c 电流为I′，损耗为 P′Δ 。R为线路电阻。可得

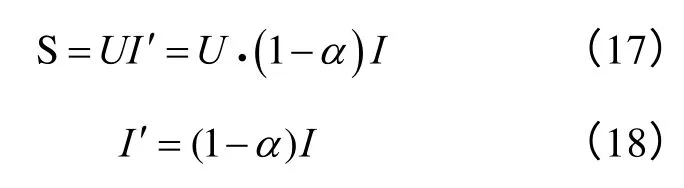
可得，简化算法计算得到的网络损耗的误差为

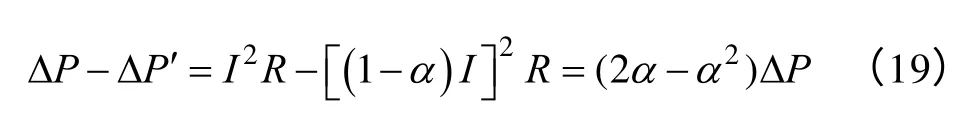
忽略电压降落时，线路损耗计算的相对误差为ε=(2α-α2)，令ε＜5%，可得α＜2.5%。综上，当电压降落低于2.5%时，忽略电压降落得到的无功损耗误差低于5%，可以采用简化的算法，如果需要更高的精度，可按照上面的公式计算允许的电压降落程度。

3.3.3 无功补偿优化算法

如3.3.2 中所述，采用基于遗传算法的无功补偿优化算法。由于直接采用配点线路中各个节点的负荷变化曲线进行计算的方式计算量巨大并且有很大的随机性，因此将各个节点的负荷数据总结成几个不同的负荷水平以及持续时间。负荷水平数越多，对负荷的分析越细致，计算的精度越高，计算方法也越复杂。通常将负荷水平分成最大负荷、平均负荷和最小负荷3 个负荷水平就可以满足优化规划的基本需求。

采用遗传算法求解配电线路潮流的主要流程如图5 所示。

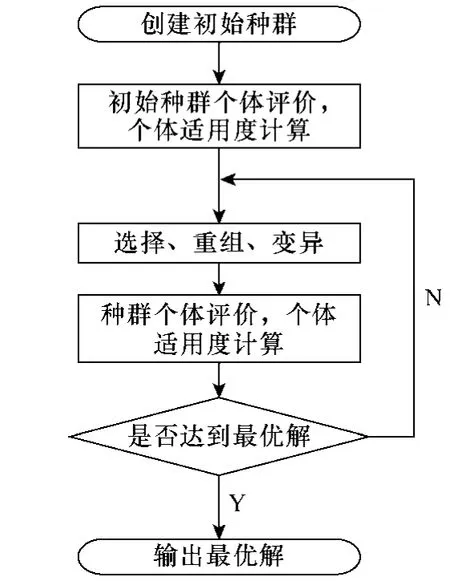
图5 遗传算法流程图Fig.5 Genetic algorithm flow

种群中每个个体的染色体上含有6 个基因，分别表示所选3 个补偿点的补偿设备的分组数和每组容量。通过潮流计算得到相应种群的状态。在一定的范围内应尽可能增大种群规模和变异率，提高遗传算法的准确度。

种群个体评价以目标函数计算所得的总体收益为准，每个个体所代表的无功补偿配置方案在不同负荷水平下投入补偿电容容量的计算流程如图6 所示。根据各个设备投入的补偿容量以及线路负荷水平计算补偿前后配电线路的潮流，以此为依据计算投资与降损收益，二者相减得出对应方案的总体收益。不同的无功规划会对有功损耗造成很大的影响，因此计算降损收益应考虑有功损耗和无功损耗之和在补偿前后的总体降损值。

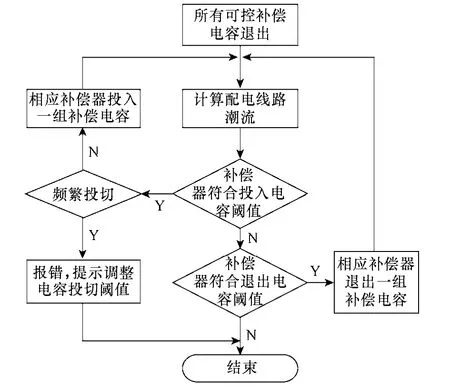
图6 补偿电容器投切计算流程Fig.6 Calculation flow of compensation capacitor switching

遗传算法存在收敛到局部最优解的现象，因此在一定的范围内应尽可能增大种群规模和变异率，在计算过程中可进行多次优化运算降低群体中所有个体陷于同一极值而停止进化的机率。

4 算例分析

基于上述的无功优化规划方法，利用Matlab 软件编写的程序，已经应用于河南某县多条10kV 线路的补偿电容器优化配置计算。下面以文献[19]的算例系统，对以上算法的有效性进行验证，其配电网单线图如图7 所示。

配电线路的导线选型和各配变之间的距离以及配变型号、线路中各配变的负荷以及持续时间均与文献[19]相同。其中122 配变的负荷与实际配电线路通常情况有所出入，本文经过对线路中其他配变负荷特点的分析，认同文献[17]对122 配变负荷水平及持续时间的调整，结果见表1。

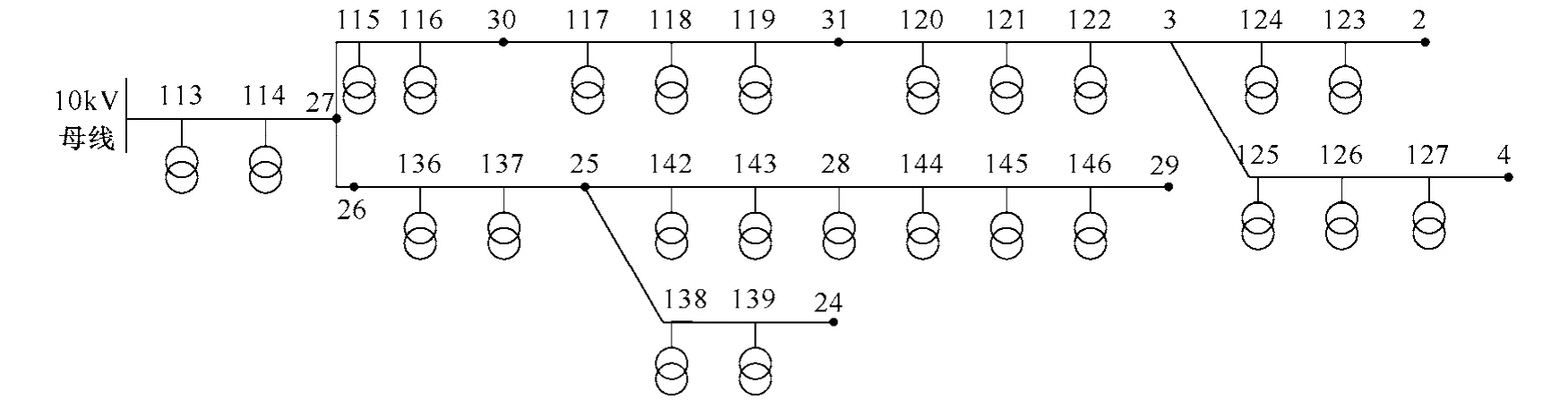
图7 配电网单线图Fig.7 Single line diagram of the distribution network

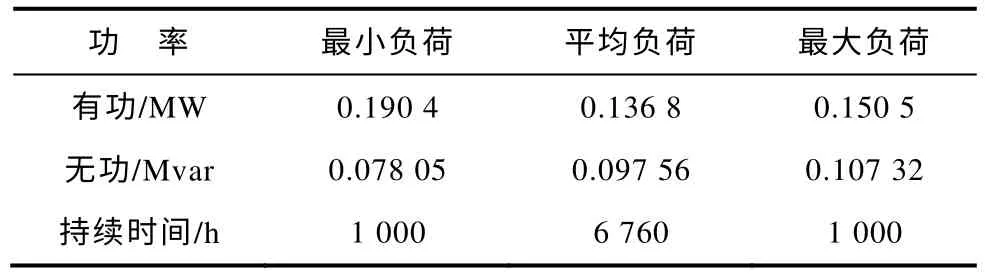
表1 节点112 配变的负荷水平及其持续时间Tab.1 Load levels and duration hours at the transformer 122

无功补偿设备参数见表2，无功优化规划计算参数见表3。表2 中分组价格比较高，原因在于设计的无功补偿设备采用了三相单独控制的真空永磁机械开关及其驱动器，提高了动作过程的时间精度。配电线路的潮流计算采用牛顿法，遗传算法种群规模为40，最大迭代代数为100，交叉率为0.9，变异率为0.001 7。

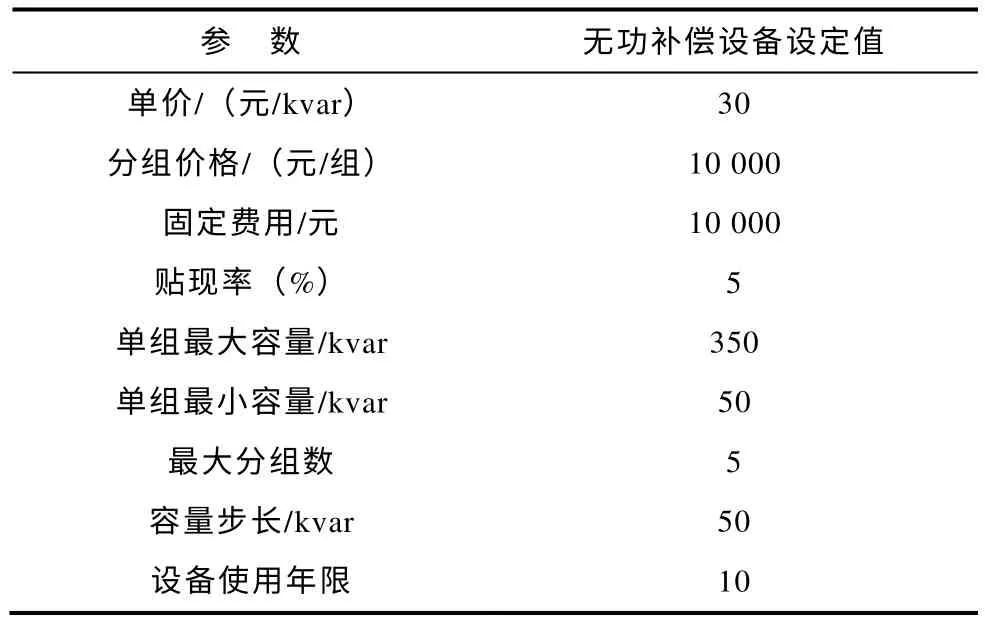
表2 无功补偿设备参数Tab.2 Parameters setting of compensation equipment

表3 无功优化规划计算约束条件Tab.3 parameters and constraints

根据灵敏度分析，并结合线路的实际负荷分布情况，选择122 号、145 号和25 号节点作为补偿点。分别对测量点与补偿点不分离的传统无功补偿设备和测量点与补偿点分离的无功补偿设备进行优化规划计算。

4.1 测量点与补偿点不分离的传统无功补偿设备

对于补偿点与测量点不分离的设备，投入补偿电容后，其所在节点的功率因数应低于0.95。无功优化规划运算的结果见表4，每年净收益为29.595万元。

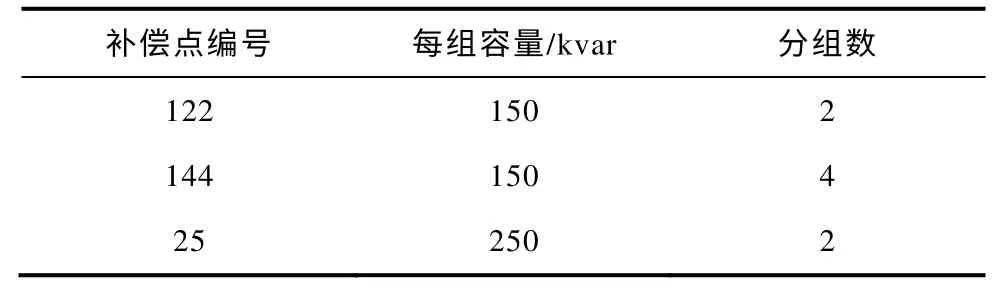
表4 传统无功补偿设备优化规划方案Tab.4 Traditional compensation results

4.2 测量点与补偿点分离的无功补偿设备

4.2.1 采用遗传算法确定测量点位置的方法

对于补偿点与测量点分离的设备，投入补偿电容后，其测量点所在节点的功率因数应低于0.95。种群中每台补偿设备在染色体上含有3 个基因，分别表示补偿设备的测量点待选节点、分组数和每组容量。

无功优化规划运算的结果见表5，每年净收益为35.774 万元，相对于补偿点与测量点不分离的设备，效益提高了16%。

表5 测量点与补偿点分离的无功补偿设备优化规划方案Tab.5 The measurement part and the compensation part separated compensation results

由于每个补偿设备有测量点位置、每组容量和分组数3 个变量，所以遗传算法的运算量巨大。

对计算结果中各节点电压进行分析，最大负荷状态下各补偿设备控制范围起止点节点电压见表6。

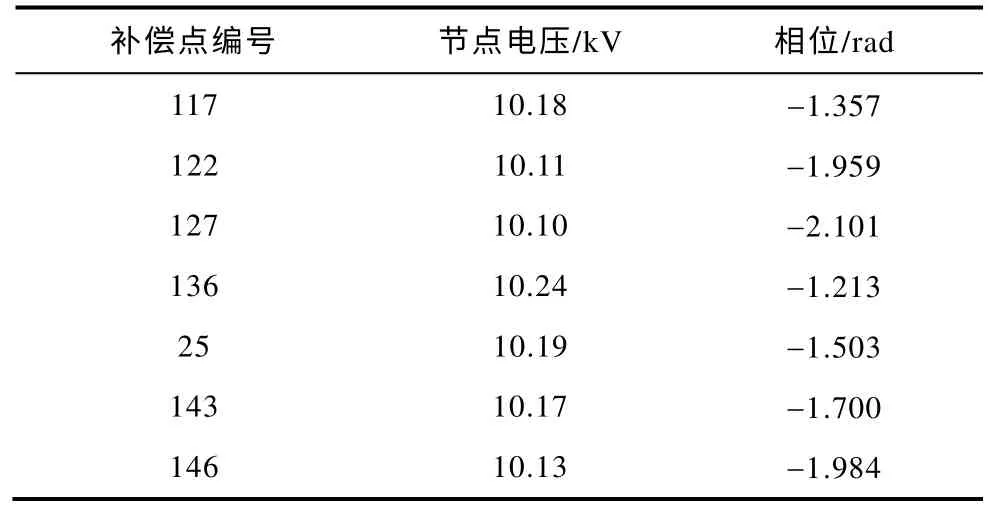
表6 最大负荷状态下关键节点电压Tab.6 Voltage of key node in maximum load

4.2.2 采用简化后算法的测量点位置确定方法

从最大负荷下各个节点的电压数据可以看出，补偿后，每台补偿设备补偿范围内各节点电压降落小于节点电压的1%。因此可以按照3.3.2 所示的测量点选取方法对遗传算法的求解过程进行简化，采用灵敏度法确定补偿点位置后，计算并确定测量点的位置，结果见表7。

表7 测量点选取结果Tab.7 The measurement part determined results

简化后，种群中每台补偿设备在染色体上还有2 个基因，分别表示补偿设备的分组数和每组补偿容量。采用遗传算法进行无功优化规划运算的结果见表8，每年净收益为35.494 万元。

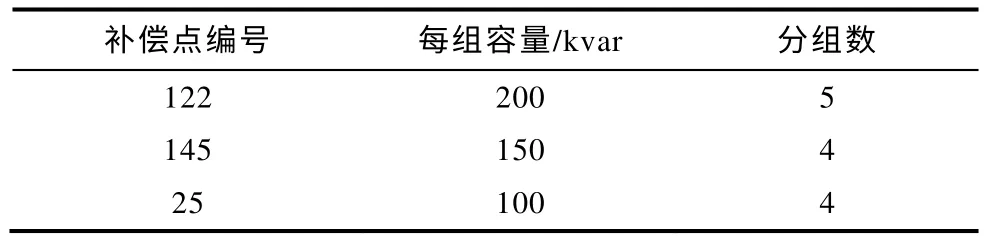
表8 简化算法无功优化规划方案Tab.8 Simplification compensation results

对比4.2.1 节和4.2.2 节的计算结果可以看出，简化后的计算结果与采用遗传算法同时确定测量点位置、每组补偿容量和分组数的方法相比，误差低于1%，满足无功优化规划运算的要求。

4.3 结果对比

结合两种方法的补偿效果和经济效益进行分析。可以得到以下分析结果：

（1）传统的无功补偿设备与测量点与补偿点分离的无功补偿设备通过无功优化规划后，都可以有效地稳定配电线路各节点电压、降低网损和提高经济效益。

（2）测量点与补偿点分离的设计保证了无功补偿设备所提供的无功输送给距离最近的无功消耗节点，最大限度地降低无功传输引起的有功和无功网损。

（3）采用基于遗传算法，对测量点、补偿容量和分组数综合寻优的计算方法以及简化后的计算方法都能有效地对测量点和补偿点分离的无功补偿设备进行优化配置。简化后的算法在电压降落率较低时可以有效降低算法的计算量，并可以保证算法的有效性和稳定性。

（4）测量点与补偿点分离的无功补偿设备可以提供更大的无功补偿容量，提高了单台无功补偿设备的利用率，其无功补偿控制范围相对于传统的无功补偿设备要大很多。

（5）测量点与补偿点分离的无功补偿设备的使用会使配电线路中个别节点出现过补偿的情况，但是配电线路整体不会出现过补偿，不会影响到配电线路的稳定。传统的无功补偿设备投入运行后，配电线路各个节点的功率因数都低于0.95，不会出现过补偿的情况。

5 结论

本文研究了中压无功优化规划问题，结合农村配电网的特点，针对无功补偿设备与无功优化规划方法之间的偏差，设计了测量点与补偿点分离的无功补偿设备。基于遗传算法，提出了补偿点和测量点位置分别选取的优化计算方法和流程。通过灵敏度分析的方法确定待选的无功补偿设备补偿点所在节点，以此为基础设计了测量点、补偿容量和分组数综合寻优的计算方法，并在电网电压降落较低的条件下对算法进行了简化处理。设计了不同负荷水平下计算补偿设备投入容量值的计算流程。通过算例对补偿点和测量点分离的无功优化规划算法进行验证，得出了在相同的线路环境以及补偿点的前提下，传统无功补偿设备和补偿点与测量点分离的补偿设备的优化结果，并进行对比分析，总结了补偿点与测量点分离的无功补偿设备的特点和需要注意的问题。

[1]吴文传,张伯明.电容器实时优化投切的最优匹配注入流法[J].中国电机工程学报,2004,24(1):35-39.Wu Wenchuan,Zhang Boming.Optimal matching injected flow for optimal sizing of capacitor[J].Proceedings of the CSEE,2004,24(1):35-39.

[2]刘蔚,韩祯祥.配电网无功补偿的动态优化算法[J].中国电机工程学报,2006,26(10):79-85.Liu Wei,Han Zhenxiang.Dynamic reactive power optimization algorithm for distribution system[J].Proceedings of the CSEE,2006,26(10):79-85.

[3]李旷,刘进军,魏标,等.静止无功发生器补偿电网电压不平衡的控制及其优化方法[J].中国电机工程学报,2006,26(5):58-63.Li Kuang,Liu Jinjun,Wei Biao,et al.Control and optimization of static VAR generator for grid voltage unbalance mitigation[J].Proceedings of the CSEE,2006,26(5):58-63.

[4]李林川,刘娜,顾丽梅.考虑静态电压稳定裕度的配电系统无功补偿优化配置[J].电工技术学报,2008,23(4):119-124,142.Li Linchuan,Liu Na,Gu Limei.Structure design of output filter in statcom and its parameter optimization[J].Transactions of China Electrotechnical Society,2008,23(4):119-124,142.

[5]王淳,程浩忠,陈恳.配电网动态无功补偿的整体优化算法[J].电工技术学报,2008,23(2):109-114.Wang Chun,Cheng Haozhong,Chen Ken.Integrated optimization algorithm of dynamic reactive power for distribution system[J].Transactions of China Electrotechnical Society,2008,23(2):109-114.

[6]邓威,李欣然,刘志勇,等.考虑无功补偿影响因素的间歇性分布式电源综合优化配置[J].中国电机工程学报,2012,32(10):80-88.Deng Wei,Li Xinran,Liu Zhiyong,et al.Comprehensive optimal allocation of intermittent distributed generation considering reactive power compensation[J].Proceedings of the CSEE,2012,32(10):80-88.

[7]吴文传,张伯明.能量损耗最小的无功补偿动态优化算法研究[J].中国电机工程学报,2004,24(4):72-77.Wu Wenchuan,Zhang Boming.Study on the alogorithm of dynamic reactive power optimization for minimal energy loss[J].Proceedings of the CSEE,2004,24(4):72-77.

[8]王威,韩学山,王勇,等.配电网络电容器优化投切的作用范围法[J].电力系统及其自动化学报,2008,20(6):36-40,69.Wang Wei,Han Xueshan,Wang Yong,et al.Action scope algorithm for optimal capacitor switching in distribution network[J].Proceedings of the CSU-EPSA,2008,20(6):36-40,69.

[9]Zhang W,Tolbert L M.Survey of reactive power planning methods[Z]:Institute of Electrical and Electronics Engineers Inc.,2005:1430-1440 BN.

[10]崔挺,孙元章,徐箭,等.基于改进小生境遗传算法的电力系统无功优化[J].中国电机工程学报,2011,31(19):43-50.Cui Ting,Sun Yuanzhang,Xu Jian,et al.Reactive power optimization of power system based on improved niche genetic algorithm[J].Proceedings of the CSEE,2011,31(19):43-50.

[11]陈树勇,申洪,张洋,等.基于遗传算法的风电场无功补偿及控制方法的研究[J].中国电机工程学报,2005,25(8):1-6.Chen Shuyong,Shen Hong,Zhang Yang,et al.Researches on the compensation and control of reactive power for wind farms based on genetic algorithm[J].Proceedings of the CSEE,2005,25(8):1-6.

[12]赵曙光,王宇平,焦李成,等.基于自适应遗传算法的无源电力滤波器综合优化方法[J].中国电机工程学报,2004,27(7):177-180.Zhao Shuguang,Wang Yuping,Jiao Licheng,et al.Adaptive genetic algorithm based optimal design approach for passive power filterS[J].Proceedings of the CSEE,2004,27(7):177-180.

[13]Abdul-Rahman K H,Shahidehpour S M.Application of fuzzy sets to optimal reactive power planning with security constraints[J].IEEE Transactions on Power Systems,1994,9(2):589-597.

[14]Venkatesh B,Sadasivam G,Khan M A.Optimal reactive power planning against voltage collapse using the successive multiobjective fuzzy LP technique[J].IEE Proceedings:Generation,Transmission and Distribution,1999,146(4):343-348.

[15]周双喜,王琦.主配电馈线上固定电容器和可调电容器的最佳配置[J].电力系统自动化,2000,24(4):37-41.Zhou Shuangxi,Wang Qi.Optimal location of fixed and switchable shunt capacitors on primary distribution feeders[J].Automation of Electric Power Systems,2000,24(4):37-41.

[16]王一杰,赵舫,丁颖,等.基于最优覆盖法的变电站无功补偿容量优化配置研究[J].电力系统保护与控制,2011,39(15):38-42.Wang Yijie,Zhao Fang,Ding Ying,et al.Research on the optimal allocation of reactive power compensation capacity based on optimal cover method[J].Power System Protection and Control,2011,39(15):38-42.

[17]胡泽春,钟明明,王佳贤,等.考虑多负荷水平的中低压配电网无功补偿优化规划[J].电工技术学报,2010,25(8):167-173.Hu Zechun,Zhong Mingming,Wang Jiaxian,et al.Optimal reactive power compensation for medium and low voltage distribution network considering multiple load levels[J].Transactions of China Electrotechnical Society,2010,25(8):167-173.

[18]王威,韩学山,王勇,等.配电网重构及电容器投切综合优化方法[J].电网技术,2010,34(12):90-93.Wang Wei,Han Xueshan,Wang Yong,et al.A compositive optimization algorithm for distribution network reconfiguration and capacitor switching[J].Power System Technology,2010,34(12):90-93.

[19]胡海燕,武晓朦,刘健.基于遗传算法的配电网低压侧无功补偿动态优化规划[J].电力自动化设备,2005,25(3):25-29.Hu Haiyan,Wu Xiaomeng,Liu Jian.Genetic algorithm based optimal dynamic planning of low-voltage side reactive power compensators[J].Electric Power Automation Equipment,2005,25(3):25-29.