粒子群优化算法综述

赵乃刚 邓景顺

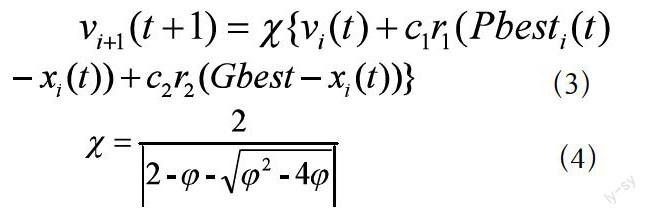
摘 要：粒子群优化算法是一种新的群智能算法。它是受自然界中鸟群、鱼群等生物的群觅食行为的启发提出的。由于该算法结构简单、需要调节的参数少，容易实现，已被很多学者研究并应用到了大量实际问题中。该文详细介绍了粒子群算法的基本原理、主要改进方法和在实际问题中的应用。

关键词：粒子群优化 元启发式算法 参数 应用

中图分类号：TP18 文献标识码：A 文章编号：1674-098X（2015）09（b）-0216-02

粒子群优化算法[1-2]是1995年由美国的心理学家Kenndy和电气工程师Eberhart首次提出来的一种新型的并行元启发式算法。该算法是模拟自然界鸟群、鱼群等生物的群觅食行为中的相互合作机制从而找到问题的最优解。由于它结构构造简单、需要调节的参数较少、涉及的专业知识少、容易实现，因此已经受到了国内外大量研究人员的广泛关注，并将它应用到了许多实际问题中。其中包括多目标优化问题[3]、非线性整数和混合整数约束优化问题[4]、信号处理[5]、神经网络训练[6]等。

该文首先介绍了标准粒子群算法的基本工作原理和算法迭代步驟，然后分别介绍了现今对粒子群算法的不同改进方法和算法在现实生活中的实际应用。在文章的结论中给出了粒子群算法下一步的研究方向。

1 标准粒子群算法

与其他的基于群体智能的算法相似，粒子群优化算法也是通过群体中不同粒子之间的相互合作和相互竞争来实现在寻优空间中的搜索过程以找到所求问题的最优位置。粒子群算法首先随机的初始化一群均匀分布在给定的寻优空间中的粒子（种群规模一般为30），然后所有的粒子根据两个极值来更新自身的速度：一个是个体极值（）；另一个是群体极值（）。目前广泛使用的标准粒子群算法的数学描述为：设粒子群中粒子的总数为，粒子的维数为，算法的终止条件（即最大迭代次数）为，第个粒子在时刻的飞行速度和在搜索空间中的位置分别为，，粒子在时刻的个体极值和群体极值分别为 ， ， 。所有的粒子按照如下的更新方式在搜索空间中飞行以找到最优解。

（1）

（2）

其中，为惯性权重系数，决定了上次迭代速度保留的多少。它是粒子群算法的重要参数之一。在粒子群算法中，可以通过调节它的大小来平衡算法的全局搜索和局部搜索的能力。研究分析表明，在粒子群算法的算法初期，选择较大的惯性权重值可以使得算法有很强的全局搜索能力；而在粒子群算法的算法后期选择较小的惯性权重值可以使得粒子逐渐收敛到全局最优。因此，在很多改进的粒子群算法中，惯性权重采用了线性递减的方式进行更新。，为算法的学习因子，它们分别影响着粒子的“自我学习”能力和“社会学习”能力。一般认为，设置较大的，会使得所有粒子过多的在局部范围内徘徊，不利于算法的全局搜索；而设置较大的，则会使得粒子过早的陷入局部极值，降低解的精度。和是介于[0，1]之间的随机数。标准粒子群算法的流程可以描述如下。

（1）设置种群规模、变量范围、惯性权重、学习因子等参数，并随机的初始化一群均匀分布在给定的寻优空间中的粒子（包含速度和位置信息）。

（2）计算群体中各个粒子的适应度值（即函数值）。设置第个粒子的适应度值为它的当前个体极值，所有粒子中的最好粒子设置为群体的全体极值。

（3）根据公式（1）、（2）更新每个粒子的速度和位置。

（4）对所有粒子，将其当前的函数值与它以前找到过的最好位置进行比较，如果当前位置较好，则将个体最优位置设置为这个粒子的位置，然后再对群体的全局极值更新。

（5）判断给定的终止条件是否满足。若满足终止条件，停止搜索，输出需要的结果；否则，返回（3）继续搜索。

2 粒子群算法的改进

粒子群算法本身也存在如下缺点。

（1）寻找到的最优解可能是局部最优解而不是全局最优解。

（2）算法搜索初期收敛速度快而搜索后期收敛速度变慢。

（3）参数选择的随机性。

为此，研究者们针对这些缺点对粒子群算法做了不同方面的改进。

2.1 添加压缩因子

Clerc M等[7]将压缩因子引入粒子群算法中，改进了算法的速度更新方式，具体如下：

（3）

（4）

其中，。一般情况下，取4.1。压缩因子的引入可以控制粒子群算法的收敛，使得粒子有机会搜索空间中不同的区域，并获得高质量的粒子。实验结果表明，它大大提高了粒子群算法的收敛速度和收敛精度。

2.2 协同粒子群算法

Vanden B F等人[8]提出了一种协同粒子群算法。该方法的具体步骤为：假设粒子的维数为，将整个粒子分为个小部分，然后算法分别对粒子的每个小部分（1维）分别进行优化，评价适应度值后合并成一个完整的粒子。结果表明了算法在很多问题上有更快的收敛速度，取得了很好的结果。

2.3 粒子群混合算法

粒子群混合算法是在粒子群算法中引入其它算法的一些比较好的思想，以提高粒子群算法的性能。这些算法包括：磷虾群算法、遗传算法、蝙蝠算法、萤火虫算法、差分进化算法等。由于这些算法有自身的优点，因此研究者们已经将它们的思想与粒子群算法结合来提高粒子群算法的性能。

2.3.1 基于自然选择机制的粒子群算法

Angeline P J [9]将自然界中的自然选择机制引入粒子群算法中，形成基于自然选择的粒子群算法。其核心思想为，当算法更新完所有的粒子后，计算粒子的适应度值并对粒子进行适应度值排序。然后根据排序结果，用粒子群体中最好的一半粒子替换粒子群体中最差的一半粒子，但是保留原来粒子的个体最优位置信息。实验结果表明，自然选择机制的引入增强了粒子的全局寻优能力，提高了解的精度。

2.3.2 基于模拟退火的粒子群算法

高鹰等人[10]提出的基于模拟退火的粒子群算法是将模拟退火机制、杂交算子、高斯变异引入粒子群算法中，以便更好的优化粒子群体。算法的基本流程是首先随机的初始一组解，通过粒子群算法的公式（1）、（2）来更新粒子，然后对所有粒子进行杂交运算和高斯变异运算，最后对每个粒子进行模拟退火运算。算法随着迭代的不断进行，温度逐渐下降，接受不良解的概率逐渐下降，从而提高了算法的收敛性。实验结果表明，改进的混合算法不仅保存了标准粒子群算法结构简单、容易实现等优点，而且由于模拟退火的引入，提高了算法的全局搜索能力、加快了算法的收敛速度、大大提高了解的精度。

3 粒子群算法应用

由于粒子群优化算法结构简单、需要调节的参数少、需要的专业知识少、实现方式容易，它一经提出，研究者们就开始尝试将它应用于各种自然科学和工程问题中去。如今，它已经被广泛的应用于函数优化、多目标优化、求解整数约束和混合整数约束优化问题、神经网络训练、信号处理等实际问题中。Tan Y等人[11]提出了一种新的混沌搜索策略，并将它引入粒子群算法中用于求解非线性整数和混合整数约束规划问题。实验结果表明，新算法大大提高了算法的收敛速度和鲁棒性；Ramadan Rabab M等人[12]将粒子群算法进行了改进并应用到了人脸识别系统中；刘元等人[13]用粒子群算法来实现锌电解优化调度；原文林等人[14]提出了基于协同进化的粒子群算法，建立了相应的惩罚因子算法评价机制，并将它用于求解比较复杂的高维梯级水库短期发电优化调度，实验结果证明了该方法的可行性和高效性，从而为求解此类问题提供了一种新的途径。

4 结语

粒子群算法一经提出便引起许多学者的广泛关注，由于它的诸多优点，它已经被改进并广泛的应用于不同现实领域中，但该算法仍然存在着许多问题值得我们进一步研究和探讨。

虽然粒子群算法的性能在不同的改进方法上有了显著的提高，但有关粒子群算法的理论基础、理论分析还很薄弱。因此，加强粒子群算法的理论分析是未来的一个重要研究方向。

针对粒子群算法易陷入局部最优、收敛性差等缺点，寻找更好的改进方法以提高其性能是必要的。

由于粒子群算法结构简单、容易实现，将它应用到更多的实际问题中也是一个热点。

参考文献

[1] Poli R，Kennedy J，Blackwell T. Particle swarm optimization[J].Swarm intelligence，2007（1）：33-57.

[2] Kennedy J.Particle swarm optimization[M].Encyclopedia of Machine Learning.Springer US，2010：760-766.

[3] Reyes-Sierra M，Coello C A C.Multi-objective particle swarm optimizers：A survey of the state-of-the-art[J].International journal of computational intelligence research，2006，2（3）：287-308.

[4] He Q，Wang L.An effective co-evolutionary particle swarm optimization for constrained engineering design problems[J].Engineering Applications of Artificial Intelligence，2006，20（1）：89-99.

[5] Melgani F， Bazi Y.Classification of electrocardiogram signals with support vector machines and particle swarm optimization[J].Information Technology in Biomedicine，IEEE Transactions on，2008，12（5）：667-677.

[6] Zhang J R，Zhang J， Lok T M， et al.A hybrid particle swarm optimization–back-propagation algorithm for feedforward neural network training[J]. Applied Mathematics and Computation，2006，185（2）：1026-1037.

[7] Clerc M，Kennedy，Télécom F. The particle swarm-explosion， stability，and convergence in a multidimensional complex space[J].Evolutionary Computation，IEEE，2002，6（1）：58-73.

[8] Vanden B F，Engelbrecht A P.Using cooperative particle swarm optimization to train product unit neural Networks[C].IEEE International Joint Conference on Neural Networks，Washington D C，USA， 2001.

[9] Angeline P J.Evolutionary optimization versus particle swarm optimization： Philosophy and performance differences[J]. Lecture Notes in Computer Science，1998：601-610.

[10] 高鷹，谢胜利.基于模拟退火的粒子群优化算法[J].计算机应用研究，2004（1）：47-50.

[11] Tan Y， Tan G， Deng S. Hybrid particle swarm optimization with chaotic search for solving integer and mixed integer programming problems[J].Journal of Central South University，2014，21（7）：2731-2742.

[12] Ramadan Rabab M，Abdel-Kader Rehab.Particle swarm optimization for human face recognition[C].IEEE International Symposiumon Signal Processing And Information Technology，ISSPIT2009，2009：579-584.

[13] 刘元，阳春华，李勇刚，等.粒子群算法在锌电解优化调度中的应用[J].自动化与仪表，2006（4）：11-14.

[14] 原文林，吴泽宁，黄强，等.梯级水库短期发电优化调度的协进化粒子群算法应用研究[J].系统工程理论与实践，2012（5）：1136-1142.