基于MATLAB/Simulink的内涨式夹紧机构运动学仿真*

金 晶，尹 铁，周 伦

(1．安瑞科廊坊能源装备集成公司，河北廊坊 065000;2．中国石油天然气管道科学研究院，河北廊坊 065000;3．廊坊职业技?术学院机械工程系，河北廊坊 065000)

0 引言

大口热煨弯管坡口机是加工热煨弯管两端坡口的专用机床［1］，内涨式夹紧机构如图1所示是弯管坡口机的核心功能部件，可以实现小尺寸空间内利用热煨弯管的内径作为定位基准，实现弯管的夹紧定位，并确保与主轴同轴，保证弯管坡口的加工质量［2］。

图1 内涨式夹紧机构三维模型与机械结构图

涨紧机构有前后两套相同的连杆机构组成，液压缸无杠腔进油推动基盘运动，基盘带动连杆推动顶杆和涨紧块实现钢管的涨紧。在每组涨紧连杆机构上均匀布置15个涨紧块，由于采用多点涨紧，可以确保在涨紧过程中各个涨紧块受力均匀。

1 机构数学模型的建立

通过分析，将内涨式夹紧机构抽取为双滑块机构进行研究分析，双滑块机构是一个具有两个移动副的平面四杆机构，可以认为是由铰链四杆机构中两杆长度趋于无穷大而演变而来的［3］。图2给出了双滑块机构的运动示意图。

图2 双滑块机构运动示意图

在分析中，每一根杆件都可以表示成一个位移矢量，矢量的起点就是杆件的某一个端点，而杆件的其另一个端点就是矢量的终点。位移矢量的大小就是杆件的长度，矢量与x轴方向间的夹角就是杆件的夹角。闭环矢量方程是机构的各个构件之间连接约束的表达式，矢量方程易于求解，而且是进行机构分析所需采取的关键一步。矢量链是用来确定机构上某一点的位置。

对于双滑块机构，通过用位移矢量来代替连杆构件，建立闭环矢量。如图3所示，取两个滑块轨道的交点为坐标系的原点，原点到滑块1的位移矢量R1，坐标原点到滑块2的位移为位移矢量R2，连接滑块1和滑块2的连杆为位移矢量R3，可以利用位移矢量来表示机构列出双滑块机构的闭环矢量方程。

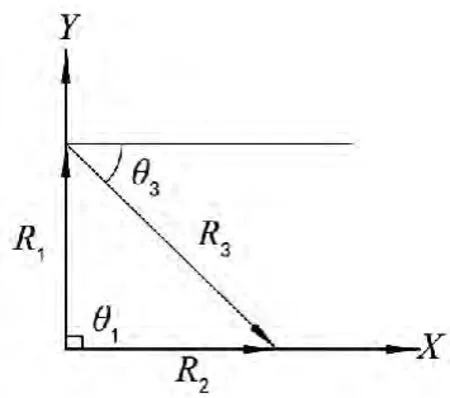
图3 双滑块机构位移矢量图

将矢量方程(1)沿x和y轴方向进行分解，可以得到两个标量方程:

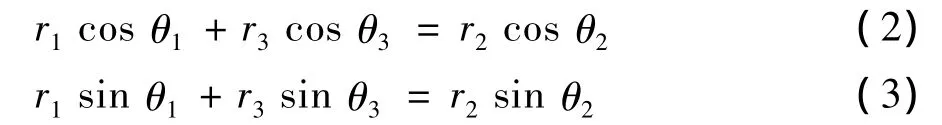
由图3 可知，在式中 θ1=90°，θ2=0°，所以式(2)和(3)可以写成:

对方程式(4)和(5)求时间导数，有:

式中:ω为θ对时间的一阶导数。式(6)和式(7)是滑块速度之间的关系，再次求导，得到各构件加速度之间的关系为:

根据对内涨式机构的分析，滑块1为主动元件，滑块2为从动元件，即是主动件，是动力输入和α3为未知量，其中ω3和θ3可由α3积分后得到，所以，式(8)和式(9)可整理成:

2 程序文件编写及矩阵求解

Matlab/Simulink中的M命令可简单的理解成以若干命令语句的集合为内容的文件。在M文件中没有输入、输出参数，只是一些命令行的集合。在程序运行时，Matlab会自动按照顺序执行文件中的各个命令行。程序运行结束后，所产生的所有变量都留存在Matlab基本工作空间中，只要不使用删除指令，这些变量就会一直存储在基本工作空间中［4］。

编写一个Matlab函数来求解方程，这个矩阵的函数文件如下，存储于文件DoubleSlider．m中，文件的内容如下:

function X=DoubleSlider(u)%u(1)=R2_Acc%u(2)=Omega1%u(3)=Theta1 R1=140;

A=［R1*cos(u(3))-1;-R1*sin(u(3))0］;

B=［R1*u(2)^2*sin(u(3));R1*u(2)^2*cos(u(3))-u(1)］;

X=inv(A)*B;%AB

3 仿真模型的建立与求解

此函数可以用Matlab中的Function块嵌入到Simulink仿真系统中，并且在Simulink图形方式中，共有6个积分模块。把各个模块用连接线连接起来，得到图4所示的Simulink仿真窗口。将DoubleSlider．m文件嵌入到Function块中，即完成了Simulink仿真模型的建立。

图4 机构仿真框图

图5 滑块2位移距离

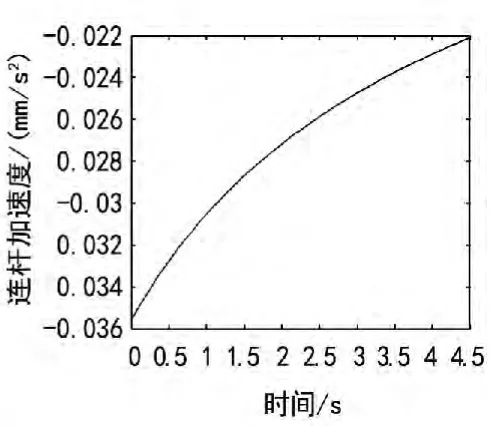
图6 连杆加速度

根据图2双滑块机构运动示意图，根据油缸工作各项参数可知，在不考虑油缸尼及爬行的情况下，假设油缸活塞杆匀速运动。则滑块1的各积分环节的积分初始值分别为v=20 mm/s，α=0 mm/s2，连杆初始θ3=47°。设定完毕后即可运行仿真，可得到图5～9的仿真结果。利用Matlab的Simulink仿真模型可以很容易得到机构各个构件的运动参数变化情况，具有可视化的特点。

图7 连杆角速度

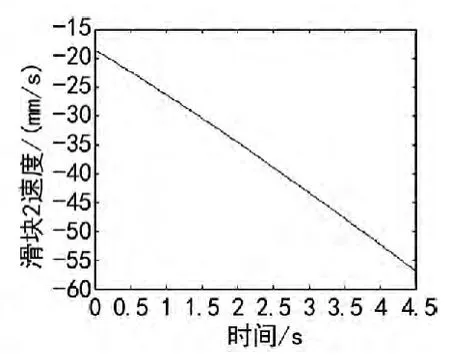
图8 滑块2速度

图9 滑块2加速度

4 结语

通过对内涨式夹紧机构进行运动仿真，形象的揭示了各个部件的运动规律，为今后相类似机构设计提供了全新的方法。通过对机构进行运动学仿真分析可为实际的生产和试验节约人力、物力和宝贵的时间，为今后热煨弯管坡口机成套化、系列化、标准化的设计具有重要的指导意义。

［1］ 尹 铁，金 晶，贾世民，等．大口径热煨弯管坡口整形机的设计［J］．管道技术与设备，2013(2):29-31．

［2］ 尹 铁，金 晶，李铁军，等．一种新型浮动切削式热煨弯管坡口机的研制［J］．机床与液压，2013，41(16):1-4．

［3］ 金 晶．面向浮动切削坡口机的新型内涨式夹紧机构的研究［D］．天津:河北工业大学，2013．

［4］ 耿珠芳，李晓亮，刘 立．基于MATLAB的双滑块机构运动学仿真［J］．冶金设备，2007(3):20-22．

［5］ 屈文涛，王亚娟 ，邹 伟，等．基于SimMechanics的牛头刨式平面六连杆机构运动学仿真［J］．机械研究与应用，2014，27(01):39-42．

［6］ 王 芳，张海燕．基于SIMULINK的连杆机构运动学仿真［J］．机械设计与研究，2004(2):35-37．

［7］ 尹 铁．大口径热煨弯管坡口机浮动切削原理及动力学性能研究［D］．天津:河北工业大学，2013．