格上时滞单种群模型的行波解的渐近性

刘艺昕， 余志先

（上海理工大学 理学院，上海 200093）

1 问题的提出

研究格上时滞单种群模型

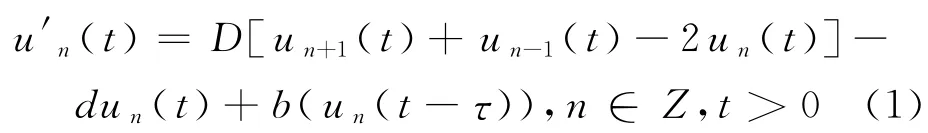
式中，D，d 分别表示成熟种群的扩散系数和死亡率，D＞0，d＞0；时滞τ 是此种群的成熟时间，τ≥0；非线性函数b（u）为出生函数.

若出生函数b∈C1（R＋）满足条件：

（H1）b′（0） ＞d，b′（u ）≥0，∀u∈（0 ，K ）有b′（0） u ≥ b （u ）＞du 及∀u ∈ （K ，＋∞）有b （u ）＜du；

（H2）b′（K ）＜d 和b（0） ＝dK－b （K ）＝0；

（H3）b′（0）u－b（u）≤Mu1＋v对于所有u∈（0 ，K ），有M ＞0和v∈（0 ，1］；

（H4）对 所 有u1，u2∈ （0 ，K ）和L ＞0，｜b′（u1）－b′（u2）｜≤L｜u1－u2｜v.

Ma等［1］在上述条件下，运用上下解和单调迭代的方法得到了行波解的存在性，并进一步研究其唯一性和稳定性.对于方程（1），其传播现象就是研究连接两个非负平衡态u1＝0 与u2＝K ＞0的行波解un（t）＝U（n＋ct）的存在性，其中，U（ξ）满足

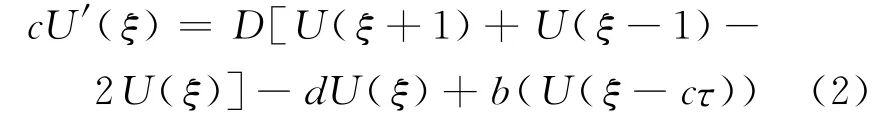
和边界条件

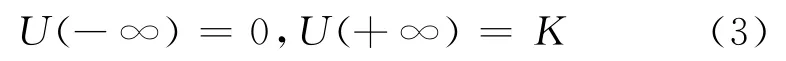
根据文献［1］的结果可知，这个行波解的指数渐近行为是仅当c＞c＊时被给出，而行波解的唯一性是在渐近条件下得到的.很自然地，会考虑下面的问题：当c＝c＊时，行波的渐近行为是怎样的，本文不仅会回答这些问题，而且得到了当c≥c＊时，所有非负行波解的渐近行为.为了说明结论，将假设条件（H3′）：b∈C2（［0 ，K ］）替 代（H3）和（H4）.易 见b∈C2（［0 ，K ］）蕴含（H3）和（H4）成立.

a. 如 果c ≥c＊，与存在.

b.如果c＝c＊，存在正数一个λ1（c＊），使得和存在，其中，λ1（c＊）是Δ （λ ，c） ＝cλ－D［eλ＋e－λ－2］的二重根.

在定理1中，得到了c＝c＊时的行波解的渐近行为，因此，完善了文献［1］中的结果.在文献［1］中，作者仅给出了存在某行波解满足渐近行为，在本文的结果中，指出所有的行波解具有指数渐近行为.

2 行波解的渐近性

Ikehara定理的渐近理论在文献［7］中用来确定非局部扩散系统行波解的渐近行为，可参见文献［8－13］.现将通过Ikehara定理的渐近理论来判定行波解的指数渐近行为.首先叙述如下Ikehara定理的渐近理论.

引理1［7］令是一个正的单调递减函数.假设l（ ）λ 可表示为，且e（λ ） 在－α≤Reλ＜0上是解析的，其中，k≥－1，则

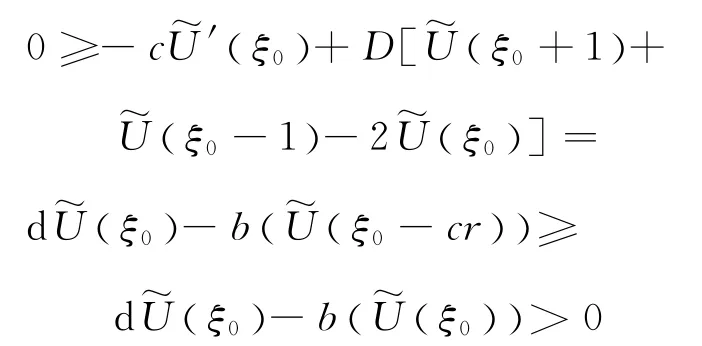
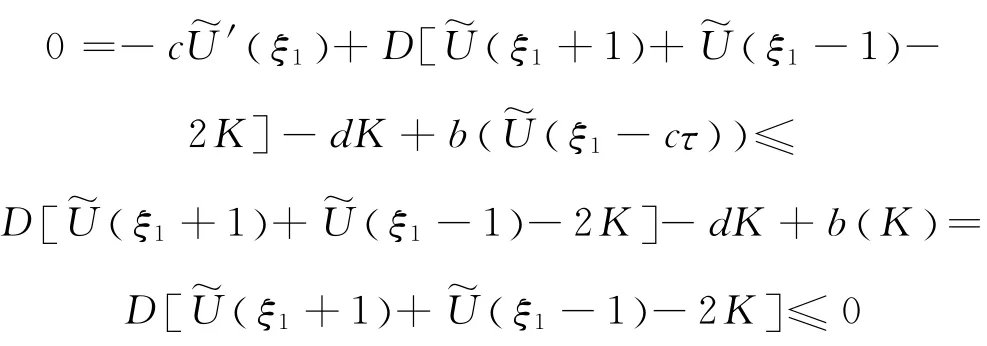
由 递 推 法，对 所 有 的 m ∈ ℤ＋，得 到，这 与U （－ ∞）＝0 矛 盾，因 此，U（ξ） ＜K，ξ∈ℝ.

其次，证明U（ξ） ＞0，ξ∈ℝ.如果存在ξ2，使得，那么，它是一个最小值，且0.由方程（2），有，这表明了.由递推法，可以得到U（ξ2＋m）＝0，对所有的m∈ℤ＋，这与U（＋∞）＝K 矛盾，于是，U（ξ） ＞0，ξ∈ℝ.

引理4 假 设（H1），（H2）和（H3′）成 立，另 外，对ξ∈ℝ，U（ξ）是非负的，则∀ξ∈ℝ，.

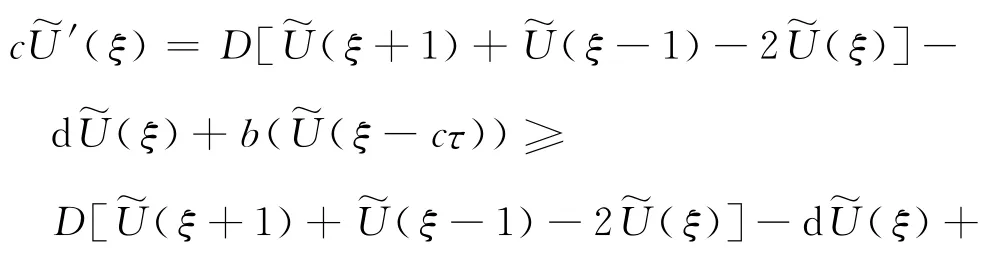
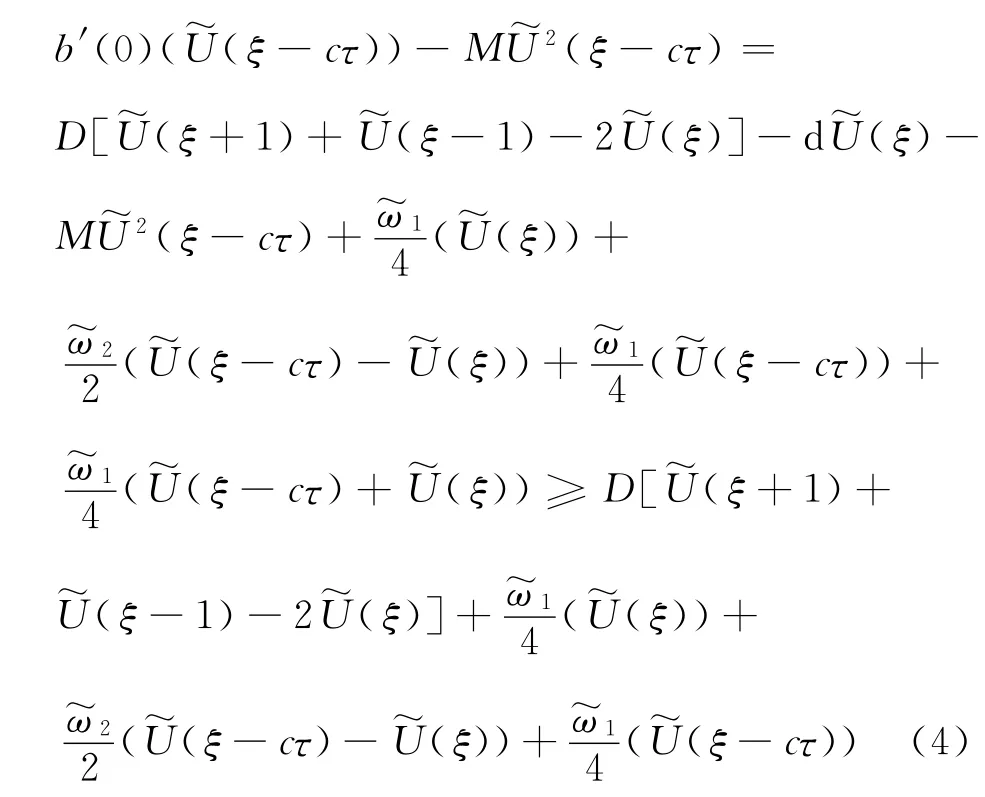
根据Lebesgue的控制收敛定理，当η→－∞时，有

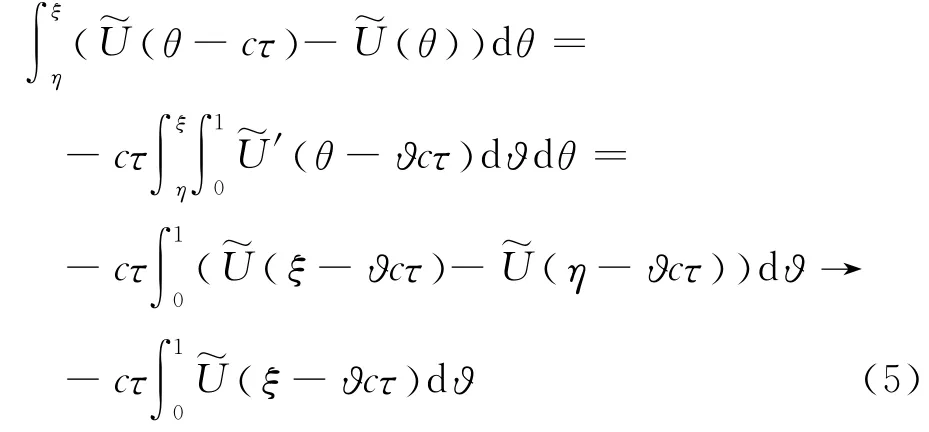
并且

对不等式（4）从－∞到ξ 进行积分，再根据式（5）和式（6），对任何ξ＜ξ′，有

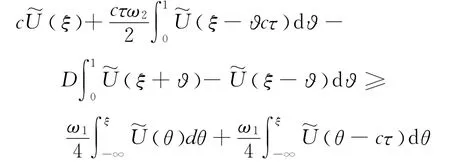
引理5 假设引理4的条件成立，那么，存在一个正的常数γ，有并且.

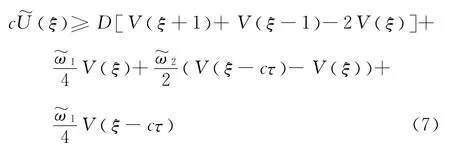
通过引理4的证明过程和对不等式（7）从－∞到ξ 进行积分，有

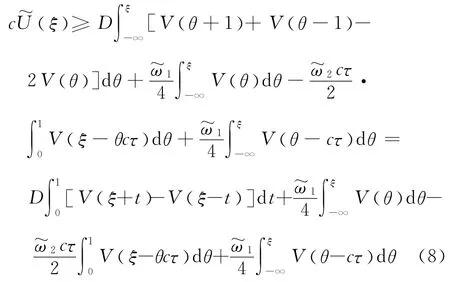
因此

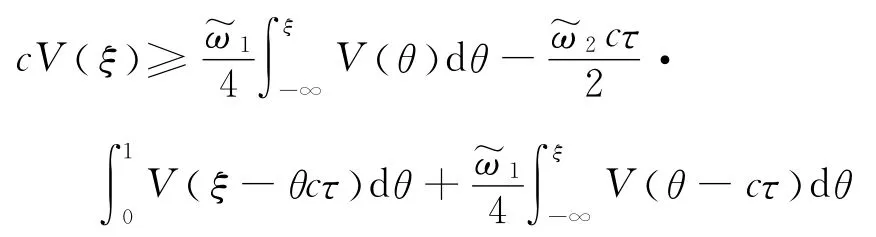
因为，V（ξ） 是非负的，得到

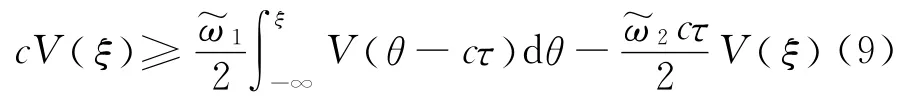
事实上，对任何的r＞0和ξ＜ξ′，由不等式（9）可以得到

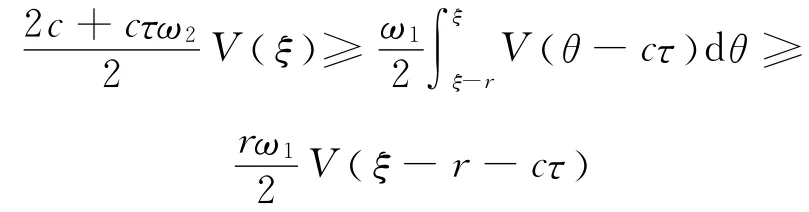
因此，存在r0＞0和，使得.

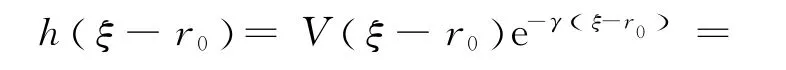
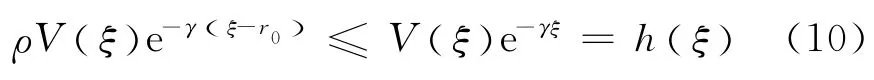
由于h（ξ） 对所有ξ∈［ξ′－r0，ξ′］是有界的，那么，不等式（10）表明了对任何ξ≤ξ′，h（ξ） 是有界的，即当ξ→－∞时，

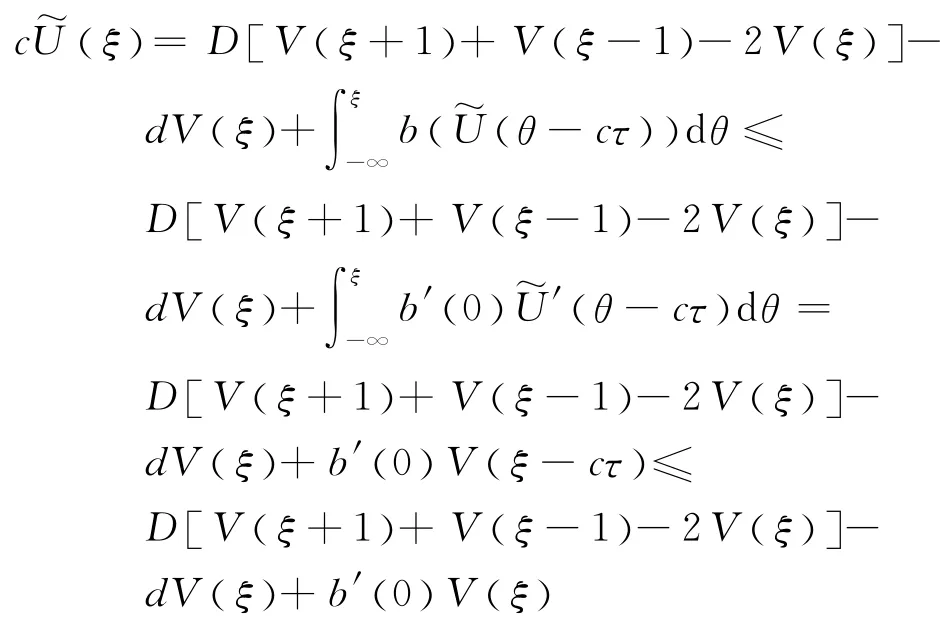
引理5表明，当0＜Reλ＜γ 时，

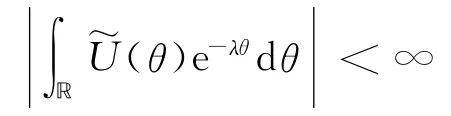
现证明定理1.

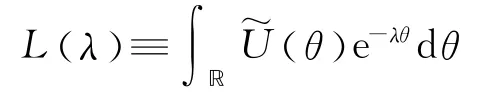
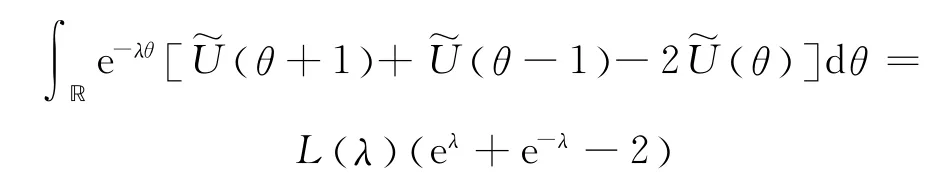
因为

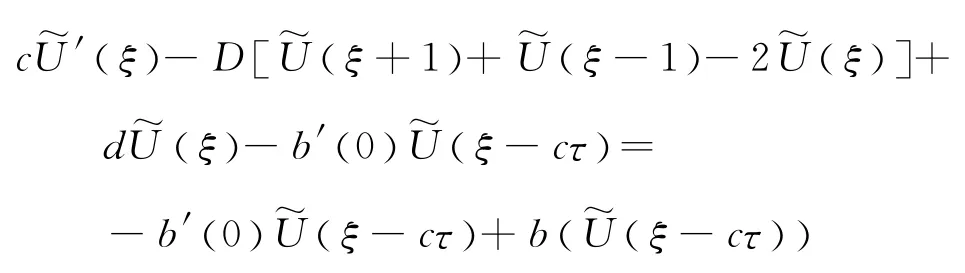
所以

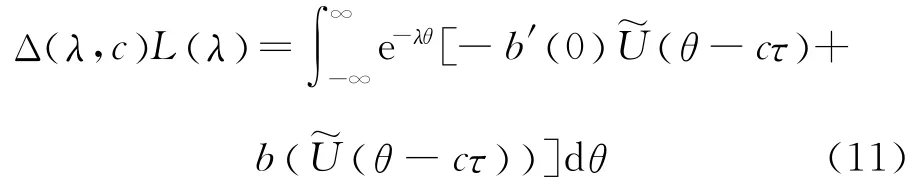
由引理2，当ξ→－∞时，得到

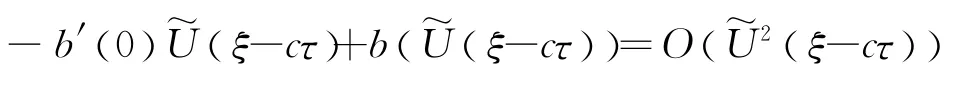
在方程（11）中的右边对于λ 在0＜Reλ＜2γ是有定义的.现在运用文献［14］中的Laplace变换的性质.因为，，存在一个正常数κ，使得对于0＜Reλ＜κ，L（λ ） 是解析的，并且L（λ ） 有一个奇点在λ＝κ.因此，当在0＜Reλ＜λ1（c） 上是有定义的.

考虑c≥c＊和.改写方程（11）为

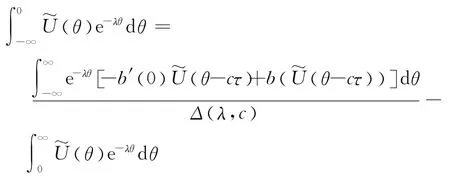
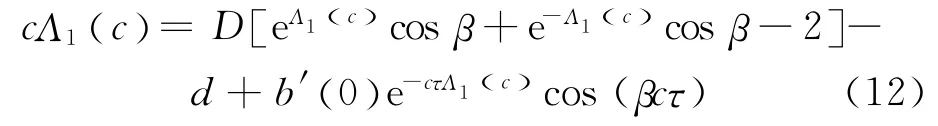
和

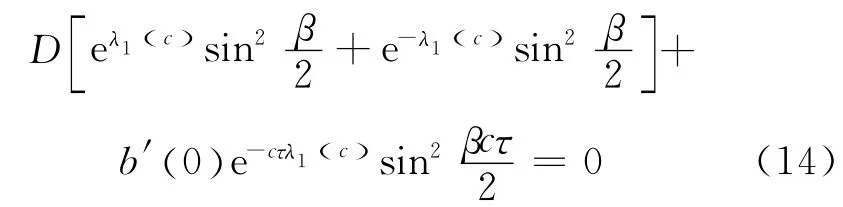
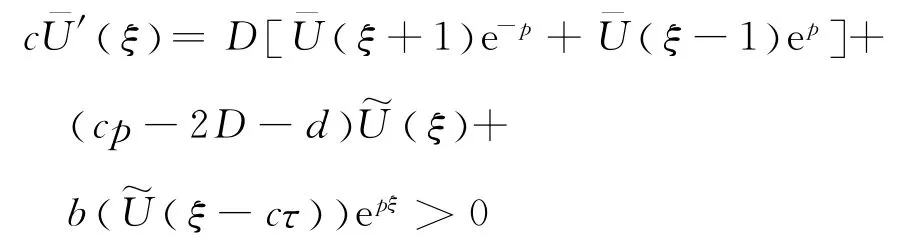
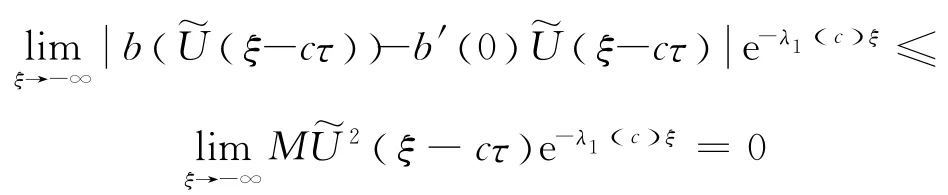
和对c＝c＊，有

因此，对于c＞c＊，有

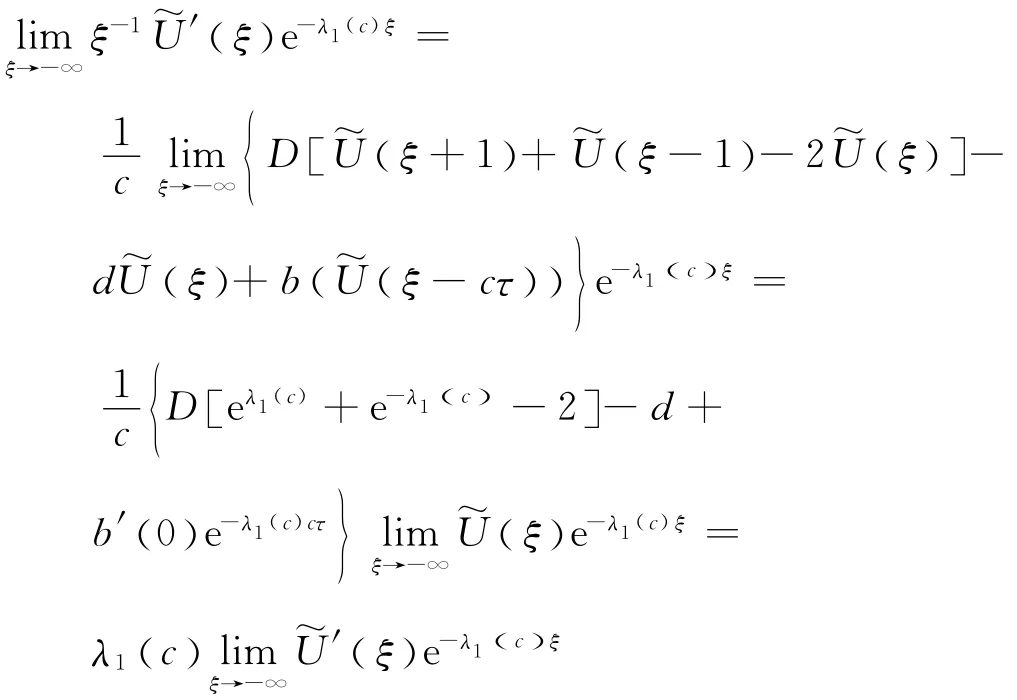
类似可以证明，当c＝c＊时结论也成立.所以，定理1得证.

［1］Ma S W，Zou X F.Existence，uniqueness and stability of traveling waves in a discrete reaction diffusion monostable equations with delay ［J］.Journal of Differential Equations，2005，217（1）：54－87.

［2］Chow S N.Lattice dynamical systems，dynamical systems［M］∥Macki J W，Zecca P eds.Dynamical Systerns，Lecture Notes in Mathematics.Berlin：Springer，2003，1822：1－102.

［3］Chow S N，Mallet－Paret J，Shen W X.Traveling waves in lattice dynamical systems［J］.Journal of Differential Equations，1998，149（2）：248－291.

［4］Keener J P.Propagation and its failure in coupled systems of discrete excitable cells［J］.SIAM Journal on Applied Mathematics，1987，47（3）：556－572.

［5］裴胜兵，张卫国，李想.色散项系数为负的MKdVBurgers方程的有界行波解［J］.上海理工大学学报，2014，36（3）：205－216.

［6］徐丽筱，张天四，黄晓鑫.一类具有饱和发生率的随机SIRS模型全局正解的渐近行为［J］.上海理工大学学报，2013，35（6）：541－546.

［7］Carr J，Chmaj A.Uniqueness of traveling waves for nonlocal monostable equations［J］.Proceedings of the American Mathematical Society，2004，132 （8）：2433－2439.

［8］Guo J S，Wu C H.Existence and uniqueness of traveling waves for a monostable 2－D lattice dynamical system［J］.Osaka Journal of Mathematics，2008，45（2）：327－346.

［9］Pan S X.Asymptotic behavior of traveling fronts of the delayed Fisher equation［J］.Nonlinear Analysis Real World Applications，2009，10（2）：1173－1182.

［10］Wang Z C，Li W T，Ruan S G.Traveling fronts in monostable equations with nonlocal delayed effects［J］.Journal of Dynamics and Differential Equations，2008，20（3）：563－607.

［11］Yu Z X.Uniqueness of critical traveling waves for nonlocal lattice equations with delays［J］.Proceedings of the American Mathematical Society，2012，140（11）：3853－3859.

［12］Yu Z X，Yuan R.Existence and asymptotics of traveling waves for nonlocal diffusion systems［J］.Chaos，Solitons ＆Fractals，2012，45（11）：1361－1367.

［13］Yu Z X，Mei M.Asymptotics and uniqueness of travelling waves for non－monotone delayed systems on 2Dlattices［J］.Canadian Mathematics Bulletin，2013，56（3）：659－672.

［14］Widder D V.The laplace tranform［M］.Princeton：Princeton University Press，1941.